devbox
在线问答5
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

略谈set与map的pair封装与进入哈希

作者：在线问答5 | 2024-08-10 20:16:02

赞

踩

略谈set与map的pair封装与进入哈希

引子：之前我们讲了红黑树的自实现，与小小的接口实现，那set与map的pair封装是如何实现的呢？，今天我们来一探究竟，而且我们也要进入新章节--哈希

对于operator--()的封装：

注意：牢记思考的方向始终是中序

示意图：

stl代码实现：

  1.   void decrement()
  2.   {
  3.     if (node->color == __rb_tree_red &&
  4.         node->parent->parent == node)
  5.       node = node->right;
  6.     else if (node->left != 0) {
  7.       base_ptr y = node->left;
  8.       while (y->right != 0)
  9.         y = y->right;
  10.       node = y;
  11.     }
  12.     else {
  13.       base_ptr y = node->parent;
  14.       while (node == y->left) {
  15.         node = y;
  16.         y = y->parent;
  17.       }
  18.       node = y;
  19.     }
  20.   }
  21. };

自实现：我们在传的时候要传一下_root,因为我们不是通过以上stl中hearer的方式

迭代器部分更改：

  1. Node* _root;
  2.  
  3. RBTreeIterator(Node*node,Node*root)
  4. 	:_node(node)
  5. 	,_root(root)
  6. {}
  1. self& operator--()
  2. {
  3. 	if (_node == nullptr) 
  4. 	{
  5. 		//找最右节点
  6. 		Node* rightMost = _root;
  7. 		while (rightMost && rightMost->_right)
  8. 		{
  9. 			rightMost = rightMost->_right;
  10. 		}
  11.  
  12. 		_node = rightMost;
  13. 	}
  14. 	else if (_node->_left)
  15. 	{
  16. 		Node* rightMost = _node->_left;
  17. 		while (rightMost->_right)
  18. 		{
  19. 			rightMost = rightMost->_right;
  20. 		}
  21.  
  22. 		_node = rightMost;
  23. 	}
  24. 	else
  25. 	{
  26. 		Node* cur = _node;
  27. 		Node* parent = cur->_parent;
  28. 		while (parent && cur == parent->_left)
  29. 		{
  30. 			cur = parent;
  31. 			parent = cur->_parent;
  32. 		}
  33.  
  34. 		_node = parent;
  35.  
  36. 	}
  37.  
  38. 	return *this;
  39. }

对于set的insert封装：

  1. //插入
  2. pair<iterator,bool>insert(const T& data)
  3. {
  4. 	//空树新增节点，也是红黑树
  5. 	Node* root = _root;
  6. 	if (root == nullptr)
  7. 	{
  8. 		root = new Node(data);
  9. 		_root = root;
  10. 		_root->_col = BLACK;
  11. 		return make_pair(iterator(_root, _root), true);
  12. 	}
  13.  
  14.     //红黑树大逻辑
  15. 	K_of_T kot;
  16. 	Node* cur = _root;
  17. 	Node* parent = nullptr;
  18.  
  19. 	//要先找到，插入位置
  20. 	while (cur)
  21. 	{
  22. 		if (kot(data) < kot(cur->_Data))
  23. 		{
  24. 			parent = cur;
  25. 			cur = cur->_left;
  26. 		}
  27. 		else if (kot(data) > kot(cur->_Data))
  28. 		{
  29. 			parent = cur;
  30. 			cur = cur->_right;
  31. 		}
  32. 		else
  33. 		{
  34. 		   return make_pair(iterator(cur, _root), false);
  35. 		}
  36. 	}
  37.  
  38. 	cur = new Node(data);
  39. 	// 新增节点。颜色红色给红色
  40. 	cur->_col = RED;
  41. 	Node* newNode = cur;
  42. 	if (kot(parent->_Data) < kot(data))
  43. 	{
  44. 		parent->_right = cur;
  45. 	}
  46. 	else
  47. 	{
  48. 		parent->_left = cur;
  49. 	}
  50. 	cur->_parent = parent;
  51.  
  52. 	//更改颜色
  53. 	//现在cur为新增节点
  54. 	while (parent && parent->_col==RED)
  55. 	{
  56. 		Node* grandfather = parent->_parent;
  57.  
  58. 		//找出叔叔节点
  59. 		if (parent == grandfather->_left)
  60. 		{
  61. 			Node* uncle = grandfather->_right;
  62. 			//情况一
  63. 			if (uncle && uncle->_col == RED)
  64. 			{
  65. 				parent->_col = BLACK;
  66. 				uncle->_col = BLACK;
  67. 				grandfather->_col = RED;
  68. 				cur = grandfather;
  69. 				parent = cur->_parent;
  70. 			}
  71. 			else
  72. 			{
  73. 				//情况二
  74. 				//    g
  75. 				//  p   u
  76. 				//c
  77. 				if (parent->_left == cur)
  78. 				{
  79. 					RotateR(grandfather);
  80. 					grandfather->_col = RED;
  81. 					parent->_col = BLACK;
  82. 				}
  83. 				else
  84. 				{
  85. 					//情况三
  86. 					//    g
  87. 					//  p   u
  88. 					//    c
  89. 					// 
  90. 					//双旋
  91. 					RotateL(parent);
  92. 					RotateR(grandfather);
  93.  
  94. 					//注意cur与parent调了一下位置
  95. 					cur->_col = BLACK;
  96. 					grandfather->_col = RED;
  97. 				}
  98. 				break;
  99. 			}
  100. 		}
  101. 		else
  102. 		{
  103. 			Node* uncle = grandfather->_left;
  104. 			//情况一
  105. 			if (uncle && uncle->_col == RED)
  106. 			{
  107. 				parent->_col = BLACK;
  108. 				uncle->_col = BLACK;
  109. 				grandfather->_col = RED;
  110. 				cur = grandfather;
  111. 				parent = cur->_parent;
  112. 			}
  113. 			else
  114. 			{ 
  115. 				//情况二
  116. 				//    g
  117. 				//  u   p
  118. 				//        c
  119. 				if (cur == parent->_right)
  120. 				{
  121. 					RotateL(grandfather);
  122. 					grandfather->_col = RED;
  123. 					parent->_col = BLACK;
  124. 				}
  125. 				//情况三
  126. 				//    g
  127. 				//  u   p
  128. 				//    c    
  129. 				else
  130. 				{
  131. 					RotateR(parent);
  132. 					RotateL(grandfather);
  133. 					cur->_col = BLACK;
  134. 					grandfather->_col = RED;
  135. 				}
  136. 				break;
  137. 			}
  138. 		}
  139. 	}
  140.  
  141. 	//确保根节点为黑的
  142. 	_root->_col = BLACK;
  143. 	return make_pair(iterator(newNode, _root), true);
  144. }

对于：map的话，只要将k对应的vaule输出就行！，注意调用的时候也要改为pair<iterator,bool>！

什么是哈希？

一，哈希是一种数学函数，它接受一个输入（或“消息”），然后返回一个通常更小的固定大小的输出，这个输出称为“哈希值”或“哈希码”。

二，哈希也是一种思想：映射：哈希思想通过哈希函数将任意长度的数据映射到固定长度的哈希值。这个映射过程是单向的，即从数据到哈希值是容易的，但从哈希值回溯到原始数据几乎是不可能的。快速性：哈希函数的设计旨在快速计算，以便在大数据集中实现高效的数据访问。均匀分布：理想情况下，哈希函数应该能够将输入数据均匀地分布在哈希值空间中，以减少冲突并提高查找效率。

哈希的应用：

哈希思想在数据库索引、密码存储、信息检索、数据同步、数字签名、区块链技术等多个领域都有广泛的应用。通过哈希，可以有效地管理和访问大量数据，同时保证数据的安全性和完整性。

由哈希来的哈希表（unordered）

一，背景：

在C++98中，STL提供了底层为红黑树结构的一系列关联式容器，在查询时效率可达到log_2N，即最差情况下需要比较红黑树的高度次，当树中的节点非常多时，查询效率也不理想。最好 的查询是，进行很少的比较次数就能够将元素找到，因此在C++11中，STL又提供了4个 unordered系列的关联式容器，这四个容器与红黑树结构的关联式容器使用方式基本类似，只是其底层结构不同，

以下是unordered_set与set的区别图，我们可以更加看到底层结构为哈希表的优势！

对于调试性能，大家可以通过以下代码进行测试：

  1. #include<unordered_set>
  2. #include<iostream>
  3. #include<set>
  4.  
  5. using namespace std;
  6.  
  7.  
  8.  
  9. int test_set2()
  10. {
  11. 	const size_t N = 10000000;
  12.  
  13. 	unordered_set<int> us;
  14. 	set<int> s;
  15.  
  16. 	vector<int> v;
  17. 	v.reserve(N);
  18. 	srand(time(0));
  19. 	for (size_t i = 0; i < N; ++i)
  20. 	{
  21. 		//v.push_back(rand()); // N比较大时，重复值比较多
  22. 		//v.push_back(rand()+i); // 重复值相对少
  23. 		v.push_back(i); // 没有重复，有序
  24. 	}
  25.  
  26. 	size_t begin1 = clock();
  27. 	for (auto e : v)
  28. 	{
  29. 		s.insert(e);
  30. 	}
  31. 	size_t end1 = clock();
  32. 	cout << "set insert:" << end1 - begin1 << endl;
  33.  
  34. 	size_t begin2 = clock();
  35. 	for (auto e : v)
  36. 	{
  37. 		us.insert(e);
  38. 	}
  39. 	size_t end2 = clock();
  40. 	cout << "unordered_set insert:" << end2 - begin2 << endl;
  41.  
  42. 	int m1 = 0;
  43. 	size_t begin3 = clock();
  44. 	for (auto e : v)
  45. 	{
  46. 		auto ret = s.find(e);
  47. 		if (ret != s.end())
  48. 		{
  49. 			++m1;
  50. 		}
  51. 	}
  52. 	size_t end3 = clock();
  53. 	cout << "set find:" << end3 - begin3 << "->" << m1 << endl;
  54.  
  55. 	int m2 = 0;
  56. 	size_t begin4 = clock();
  57. 	for (auto e : v)
  58. 	{
  59. 		auto ret = us.find(e);
  60. 		if (ret != us.end())
  61. 		{
  62. 			++m2;
  63. 		}
  64. 	}
  65. 	size_t end4 = clock();
  66. 	cout << "unorered_set find:" << end4 - begin4 << "->" << m2 << endl;
  67.  
  68. 	cout << "插入数据个数：" << s.size() << endl;
  69. 	cout << "插入数据个数：" << us.size() << endl << endl;
  70.  
  71. 	size_t begin5 = clock();
  72. 	for (auto e : v)
  73. 	{
  74. 		s.erase(e);
  75. 	}
  76. 	size_t end5 = clock();
  77. 	cout << "set erase:" << end5 - begin5 << endl;
  78.  
  79. 	size_t begin6 = clock();
  80. 	for (auto e : v)
  81. 	{
  82. 		us.erase(e);
  83. 	}
  84. 	size_t end6 = clock();
  85. 	cout << "unordered_set erase:" << end6 - begin6 << endl << endl;
  86.  
  87. 	return 0;
  88. }
  89.  
  90.  
  91. int main()
  92. {
  93.  
  94. 	test_set2();
  95.  
  96. 	return 0;
  97. }

可以有以下的结果：只展示一种

哈希函数

引起哈希冲突的一个原因可能是：哈希函数设计不够合理。

哈希函数设计原则：

哈希函数的定义域必须包括需要存储的全部关键码，而如果散列表允许有m个地址时，其值 域必须在0到m-1之间

哈希函数计算出来的地址能均匀分布在整个空间中

哈希函数应该比较简单

常见的哈希函数包括以下几种类型：(最常用的，用颜色标出了)

直接定址法：使用关键字本身作为哈希地址，例如年龄作为关键字时，年龄值直接作为哈希地址 

数字分析法：选择数字的某些部分作为哈希地址，避免使用重复可能性大的数字前几位 

平方取中法：取关键字平方后的中间几位作为哈希地址 

折叠法：将关键字分割成位数相同的几部分，然后取这几部分的叠加和作为哈希地址 

除留余数法：使用关键字除以一个不大于哈希表大小的数后的余数作为哈希地址，公式为 H(key) = key%p (p ≤ m) ;

随机数法：使用随机函数作为哈希地址，适用于关键字长度不等的情况 

加法哈希：通过将字符串中每个字符的ASCII值累加得到哈希值 

位运算Hash：利用位运算（如移位和异或）混合输入元素，例如旋转Hash 

乘法Hash：使用乘法的不相关性，例如使用乘数31的String类的hashCode()方法 

除法Hash：虽然不常用，但除法也具有不相关性，可以用于哈希函数 

查表Hash：如CRC系列算法，通过查找预设的表来实现快速哈希 

混合哈希算法：结合以上各种方式，例如MD5、Tiger等，它们通常用于需要高安全性的场合 

哈希冲突解决

哈希冲突

哈希冲突，也称为哈希碰撞，是指两个不同的输入值通过哈希函数计算后得到相同的哈希值。由于哈希函数的输出长度是固定的，而输入数据可以是无限的，理论上讲，任何哈希函数都可能发生冲突.

解决哈希冲突两种常见的方法是：闭散列和开散列

一，什么是闭散列

也叫开放定址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有 空位置，那么可以把key存放到冲突位置中的“下一个” 空位置中去。那如何寻找下一个空位置 呢？

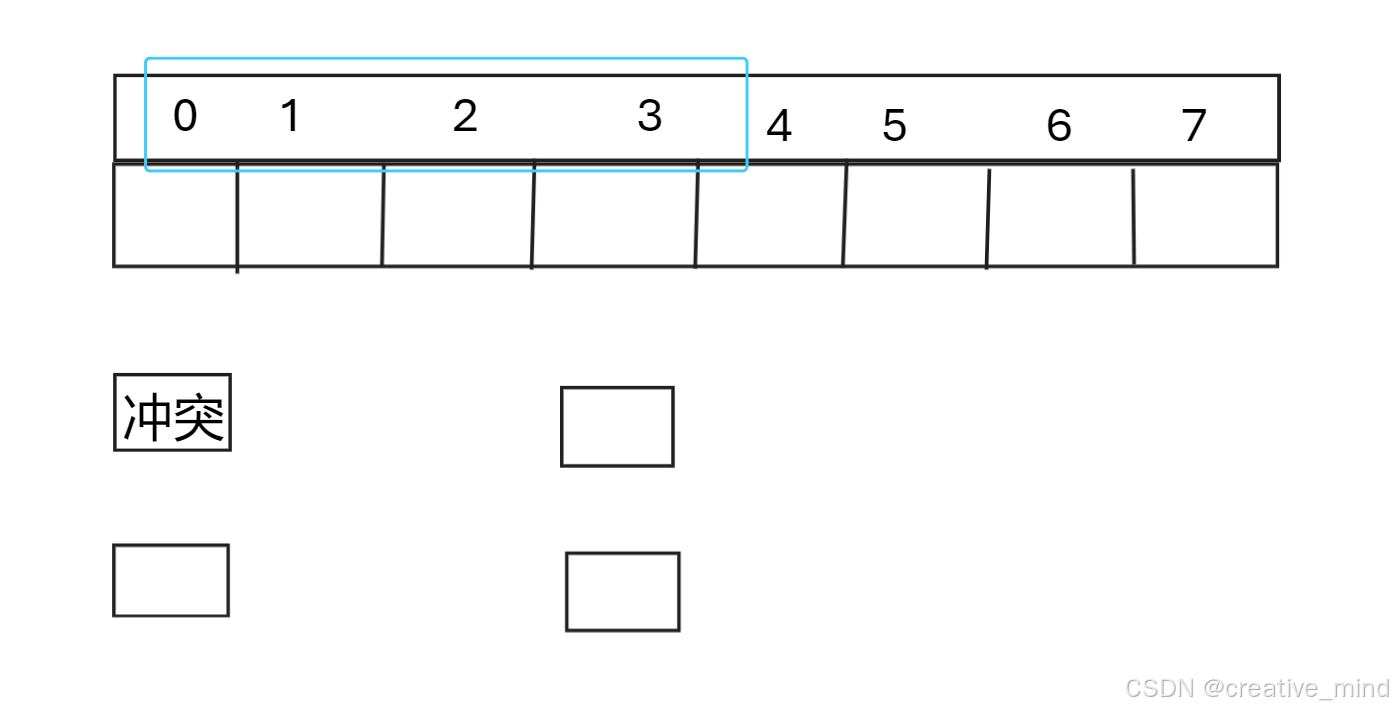
1.1，线性探测（需要枚举3种状态）

  1. 计算哈希值：首先，使用哈希函数计算键（key）的哈希值，确定它在哈希表中的理论位置。

  2. 检查冲突：如果该位置已被占用（即发生冲突），则按照固定间隔（通常是1）移动到下一个位置。

  3. 探测序列：继续线性地探测下一个位置，直到找到一个空闲位置。

  4. 插入元素：一旦找到空闲位置，将元素插入到该位置。

  5. 处理表满：如果探测到表的末尾仍未找到空闲位置，则循环回到表的开头继续探测。

  6. 查找元素：在查找元素时，也需要从哈希值对应的位置开始，按照相同的探测序列查找，直到找到目标元素或遇到一个空闲位置（表示元素不存在）。

  7. 删除元素：删除元素时，不能简单地将位置置为空，因为这会打断查找其他元素的探测序列。通常使用一个特殊的标记（如“已删除”标记）来代替真正的空位。

1.2，二次探测（需要枚举3种状态）

  1. 计算哈希值：首先，使用哈希函数计算键的哈希值，确定它在哈希表中的理论位置。

  2. 发生冲突：如果该位置已被占用，计算下一个探测位置，公式为： 探测位置=(原始位置)+i^2 其中 i 是探测的第几次尝试（i=1,2,3,…）

  3. 探测序列：探测位置是原始哈希值加上 i^2 的结果，这样探测的间隔会随着 i 的增加而增加（1, 4, 9, 16, ...）。

  4. 插入元素：当找到一个空闲位置时，将元素插入到该位置。

  5. 循环探测：如果探测到表尾，继续从表头开始探测，直到找到空闲位置。

  6. 查找元素：查找时，也需要按照相同的探测序列进行查找，直到找到目标元素或确定元素不存在。

  7. 删除元素：与线性探测类似，不能简单地将位置置为空，而是使用一个特殊的标记来表示该位置已被删除。

其他：平衡因子：

哈希的平衡因子，也称为荷载因子（Load Factor），是衡量哈希表性能的一个重要参数。它定义为哈希表中已存储元素的数量与哈希表的总槽位数（即哈希表的大小）之比。荷载因子用以下公式表示

荷载因子=已存储元素的数量​/哈希表的大小

荷载因子反映了哈希表的填充程度，对哈希表的性能有直接影响

二，什么是开散列，就是说

开散列法又叫链地址法(开链法)，首先对关键码集合用散列函数计算散列地址，具有相同地 址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链 接起来，各链表的头结点存储在哈希表中。

下节，我将详细讲解哈希表，已经自实现！，希望帮到大家！

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/在线问答5/article/detail/960204
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号