机器人中的数值优化（十九）—— SOCP锥规划应用：时间最优路径参数化(TOPP)_topp问题

   本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考，主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等，本系列文章篇数较多，不定期更新，上半部分介绍无约束优化，下半部分介绍带约束的优化，中间会穿插一些路径规划方面的应用实例

---

---

  

   三十一、时间最优路径参数化(TOPP)

   如果我们有一条二阶连续可微的路径q，现在我们想要机器人去跟踪这个路径，需要给这条路径加入时间属性，同时使其满足机器人的动力学约束，路径可由弧长s变量参数化，将路径分割成若干段小路径，我们可以知道每段小路径对应的空间位置，但是缺乏时间属性，TOPP就是在给定的平滑路径$q(s)$上生成时间信息，并使得在满足机器人动力学约束的前提下，路径花费的时间应该尽可能短。

   使用弧长参数s来对路径进行参数化，s的值表征的是距离路径起点所走过的路径距离，在下图的例子中，左下角路径的起点处s=0，右上角路径的终点处s=L，L即该路径的总长度，对于该路径，我们可以用$\frac{\mathrm{d}s}{\mathrm{d}t}$来表征路径上某个位置处的速度，它是连续的，如下图中右下角的曲线所示，同理，可以用$\frac{{\mathrm{d}}^{2}s}{\mathrm{d}{t}^2}$来表征路径上某个位置处的加速度，它可以是不连续的，如下图中左上角的曲线所示。

–

   现在，我们假设把s拉成直线，对于匀加速运动，起点s=0处的速度为$v_0$，终点s=L处的速度为$v_L$，由基础的物理学公式可知 $v_L^2-v_0^2=2aL$，进一步可知:

   $$\underset{L\to 0}{\lim }\frac{V_L^2-V_0^2}{L}=2a$$

   也即$\frac{d{v}^2}{ds}=2a$，我们得到了一个不依赖于时间属性的微分关系，我们以弧长s为参量的话，$v^2$与2a是线性的微分关系，$v^2$可以用${\left(\frac{\mathrm{d}s}{\mathrm{d}t}\right)}^2$表示

   通过类比以上速度和加速度的概念，我们可以得到

   a ( s ) = d 2 s d t 2 , b ( s ) = ( d s d t ) 2 v s 2 − v 0 2 = 2 a s b ′ ( s ) = 2 a ( s )

$$\begin{gathered}a(s)=\frac{\mathrm{d}^2s}{\mathrm{d}t^2},b(s)=(\frac{\mathrm{d}s}{\mathrm{d}t})^2\\\\v_s^2-v_0^2=2as\\\\b^{\prime}(s)=2a(s)\end{gathered}$$ a(s)=dt2d2s​,b(s)=(dtds​)2vs2​−v02​=2asb′(s)=2a(s)​

   其实，我们想要在一系列的约束下，找一个s与s’的时间最优的轨迹

   我们想要整个轨迹在动力学约束下时间最短，也就是最小化总的时间T，由于我们缺乏时间信息，所以，需要进行换元，将对时间的积分转换成对弧长s的积分，如下式所示：

   $$T={\int }_0^{T}1\mathrm{d}t={\int }_{s(0)}^{s(T)}\frac{1}{\mathrm{d}s/\mathrm{d}t}\mathrm{d}s={\int }_0^L\frac{1}{\mathrm{d}s/\mathrm{d}t}\mathrm{d}s={\int }_0^L\frac{1}{\sqrt{b(s)}}\mathrm{d}s$$

   利用链式求导法则可以得到真实的速度$\frac{\mathrm{d}q}{\mathrm{d}t}$和加速度$\frac{{\mathrm{d}}^{2}q}{\mathrm{d}{t}^2}$，分别与$\frac{\mathrm{d}s}{\mathrm{d}t}$、$\frac{{\mathrm{d}}^{2}s}{\mathrm{d}{t}^2}$的关系，如下所示：

   $$\frac{\mathrm{d}q}{\mathrm{d}t}=q^{\prime }(s)\frac{\mathrm{d}s}{\mathrm{d}t}=q^{\prime }(s)\sqrt{b(s)}$$

   $$\frac{{\mathrm{d}}^{2}q}{\mathrm{d}{t}^2}=q^{\prime \prime }(s){\left(\frac{\mathrm{d}s}{\mathrm{d}t}\right)}^2+q^{\prime }(s)\frac{{\mathrm{d}}^{2}s}{\mathrm{d}{t}^2}=q^{\prime \prime }(s)b(s)+q^{\prime }(s)a(s)$$

   若我们只考虑向前运动的情况，则b(s)≥0应该严格成立，并仅在某个或某几个瞬间为0.

   因此，我们可以将这个简单的TOPP问题表述为：

   min ⁡ a ( s ) , b ( s ) ∫ 0 L 1 b ( s ) d s s . t . b ( s ) ≥ 0 , ∀ s ∈ [ 0 , L ] , b ′ ( s ) = 2 a ( s ) , ∀ s ∈ [ 0 , L ] , ∥ q ′ ( s ) b ( s ) ∥ ∞ ≤ v m a x , ∀ s ∈ [ 0 , L ] , ∥ q ′ ′ ( s ) b ( s ) + q ′ ( s ) a ( s ) ∥ ∞ ≤ a m a x , ∀ s ∈ [ 0 , L ] , b ( 0 ) = b 0 ,   b ( L ) = b L .

$$\begin{aligned} \min_{a(s),b(s)}& \int_0^{\color{blue}{L}}\frac{1}{\sqrt{b(s)}}\mathrm{d}s \\ \mathrm{s.t.}& b(s)\geq0, \forall s\in[0,L], \\ &b^{\prime}(s)=2a(s), \forall s\in[0,L], \\ &\left\|\color{blue}{q^{\prime}(s)}\color{black}\sqrt{b(s)}\right\|_\infty\leq\color{blue}{v_{max}}, \color{black}\forall s\in[0,L], \\ &\left\|\color{blue}{q^{\prime\prime}(s)\color{black}b(s)+\color{blue}q^{\prime}(s)\color{black}a(s)}\right\|_\infty\leq\color{blue}{a_{max}},\color{black}\quad\forall s\in[0,L], \\ &b(0)=\color{blue}{b_0},\color{black}~b(L)=\color{blue}{b_L}. \end{aligned}$$ a(s),b(s)min​s.t.​∫0L​b(s) ​1​dsb(s)≥0,∀s∈[0,L],b′(s)=2a(s),∀s∈[0,L], ​q′(s)b(s) ​ ​∞​≤vmax​,∀s∈[0,L],∥q′′(s)b(s)+q′(s)a(s)∥∞​≤amax​,∀s∈[0,L],b(0)=b0​, b(L)=bL​.​

   其中${\min }_{a(s),b(s)}{\int }_0^L\frac{1}{\sqrt{b(s)}}\mathrm{d}s$是我们优化的目标函数，即时间最短，$b(s)\ge 0$用于确保s关于t的变化率的平方是非负的，$b^{\prime }(s)=2a(s)$是前面推导出其满足的物理关系式，${\Vert q^{\prime }(s)\sqrt{b(s)}\Vert }_{\infty }\le v_{max}$即任意弧长在s处的速度要满足动力学约束，同理${\Vert q^{\prime \prime }(s)b(s)+q^{\prime }(s)a(s)\Vert }_{\infty }\le a_{max}$任意弧长在s处的加速度要满足动力学约束，$b(0)=b_0,b(L)=b_L$是让s对t变化率的平方在开始和结束时的值是我们人为给定的。

   此外，上式中的蓝色部分都是已知的常数，我们要求的优化变量是a(s)和b(s)这两个凸函数，也即以函数为优化变量的凸问题。

   以函数为优化变量的凸问题，在计算机里面不能处理连续时间的问题，我们需要对其进行离散化，即把路径分割成若干段小路径，在每段小路径上，$a^i$是一个常数，$b^i$是一个线性的函数，如下图所示

   离散化后的数学表达式如下所示：

   ∫ 0 L 1 b ( s ) d s ⇔ ∑ k = 0 K − 1 2 ( s k + 1 − s k ) b k + 1 + b k b ( s ) ≥ 0 , ∀ s ∈ [ 0 , L ] ⇔ b k ≥ 0 , 0 ≤ k ≤ K b ′ ( s ) = 2 a ( s ) , ∀ s ∈ [ 0 , L ] ⇔ b k + 1 − b k s k + 1 − s k = 2 a k , 0 ≤ k ≤ K ∣ q ′ ( s ) b ( s ) ∥ ∞ ≤ v m a x , ∀ s ∈ [ 0 , L ] ⇔ ∥ q ′ ( s k ) b k ∥ ∞ ≤ v m a x , 0 ≤ k ≤ K ∥ q ′ ′ ( s ) b ( s ) + q ′ ( s ) a ( s ) ∥ ∞ ≤ a m a x , ∀ s ∈ [ 0 , L ] ⇔ ∥ q ′ ′ ( s k ) b k + q ′ ( s k ) a k ∥ ∞ ≤ a m a x , 0 ≤ k ≤ K

$$\begin{aligned} \int_{0}^{L}\frac{1}{\sqrt{b(s)}}\mathrm{d}s& \Leftrightarrow\sum_{k=0}^{K-1}\frac{2(s^{k+1}-s^k)}{\sqrt{b^{k+1}}+\sqrt{b^k}} \\ b(s)\geq0,\forall s\in[0,L]& \Leftrightarrow b^k\geq0,0\leq k\leq K \\ b^{\prime}(s)=2a(s),\forall s\in[0,L]& \Leftrightarrow\frac{b^{k+1}-b^k}{s^{k+1}-s^k}=2a^k,0\leq k\leq K \\ \left|q^{\prime}(s)\sqrt{b(s)}\right\Vert_{\infty}\leq v_{max},\forall s\in[0,L]& \Leftrightarrow\left\|q^{\prime}(s^k)\sqrt{b^k}\right\|_\infty\leq v_{max},0\leq k\leq K \\ \left\|q^{\prime\prime}(s)b(s)+q^{\prime}(s)a(s)\right\|_{\infty}\leq a_{max},\forall s\in[0,L]& \Leftrightarrow\left\|q^{\prime\prime}(s^k)b^k+q^{\prime}(s^k)a^k\right\|_\infty\leq a_{max},0\leq k\leq K \end{aligned}$$ ∫0L​b(s) ​1​dsb(s)≥0,∀s∈[0,L]b′(s)=2a(s),∀s∈[0,L] ​q′(s)b(s) ​ ​∞​≤vmax​,∀s∈[0,L]∥q′′(s)b(s)+q′(s)a(s)∥∞​≤amax​,∀s∈[0,L]​⇔k=0∑K−1​bk+1 ​+bk ​2(sk+1−sk)​⇔bk≥0,0≤k≤K⇔sk+1−skbk+1−bk​=2ak,0≤k≤K⇔ ​q′(sk)bk ​ ​∞​≤vmax​,0≤k≤K⇔ ​q′′(sk)bk+q′(sk)ak ​∞​≤amax​,0≤k≤K​

   我们现在已经把以函数为优化变量的凸优化转换成了以离散序列$a^0$ ~ $a^{k-1}$、$b^0$ ~ $b^{k-1}$为优化变量的优化问题，其约束都是线性的等式或不等式。

   $$\underset{a^k,b^k}{\min }\boxed{\sum _{k=0}^{K-1}\frac{2(s^{k+1}-s^k)}{\sqrt{b^{k+1}}+\sqrt{b^k}}}$$

   b k ≥ 0 , 0 ≤ k ≤ K b k + 1 − b k = 2 ( s k + 1 − s k ) a k , 0 ≤ k ≤ K ∥ q ′ ( s k ) b k ∥ ∞ ≤ v m a x , 0 ≤ k ≤ K ∥ q ′ ′ ( s k ) b k + q ′ ( s k ) a k ∥ ∞ ≤ a m a x , 0 ≤ k ≤ K

$$\begin{aligned}&b^k\geq0,\quad&0\leq k\leq K\\&b^{k+1}-b^k=2(s^{k+1}-s^k)a^k,\quad&0\leq k\leq K\\&\left\|q^{\prime}(s^k)\sqrt{b^k}\right\|_\infty\leq v_{max},\quad&0\leq k\leq K\\&\left\|q^{\prime\prime}(s^k)b^k+q^{\prime}(s^k)a^k\right\|_\infty\leq a_{max},\quad&0\leq k\leq K\end{aligned}$$ ​bk≥0,bk+1−bk=2(sk+1−sk)ak, ​q′(sk)bk ​ ​∞​≤vmax​, ​q′′(sk)bk+q′(sk)ak ​∞​≤amax​,​0≤k≤K0≤k≤K0≤k≤K0≤k≤K​

   $$b(0)=b_0,b(L)=b_L.$$

   那么。我们如何将以上问题转化为锥规划问题呢？可以对优化的目标函数进行如下的转换：

   至此，我们得到了该问题的SOCP形式如下：

   min ⁡ a k , b k , c k , d k ∑ k = 0 K − 1 2 ( s k + 1 − s k ) d k ∥ 2 c k + 1 + c k − d k ∥ 2 ≤ c k + 1 + c k + d k , 0 ≤ k ≤ K − 1 ∥ 2 c k b k − 1 ∥ 2 ≤ b k + 1 , 0 ≤ k ≤ K .

$$\begin{aligned}&\min_{a^k,b^k,c^k,d^k}\sum_{k=0}^{K-1}2(s^{k+1}-s^k)d^k\\&\begin{Vmatrix}2\\c^{k+1}+c^k-d^k\end{Vmatrix}_2\leq c^{k+1}+c^k+d^k,\quad0\leq k\leq K-1\\\\&\left\|\begin{array}{c}2c^k\\b^k-1\end{array}\right\|_2\leq b^k+1,\quad&0\leq k\leq K.\end{aligned}$$ ​ak,bk,ck,dkmin​k=0∑K−1​2(sk+1−sk)dk ​2ck+1+ck−dk​ ​2​≤ck+1+ck+dk,0≤k≤K−1 ​2ckbk−1​ ​2​≤bk+1,​0≤k≤K.​

   b k ≥ 0 , 0 ≤ k ≤ K b k + 1 − b k = 2 ( s k + 1 − s k ) a k , 0 ≤ k ≤ K ∥ q ′ ( s k ) b k ∥ ∞ ≤ v m a x , 0 ≤ k ≤ K ∥ q ′ ′ ( s k ) b k + q ′ ( s k ) a k ∥ ∞ ≤ a m a x , 0 ≤ k ≤ K

$$\begin{aligned}&b^k\geq0,\quad&0\leq k\leq K\\&b^{k+1}-b^k=2(s^{k+1}-s^k)a^k,\quad&0\leq k\leq K\\&\left\|q^{\prime}(s^k)\sqrt{b^k}\right\|_\infty\leq v_{max},\quad&0\leq k\leq K\\&\left\|q^{\prime\prime}(s^k)b^k+q^{\prime}(s^k)a^k\right\|_\infty\leq a_{max},\quad&0\leq k\leq K\end{aligned}$$ ​bk≥0,bk+1−bk=2(sk+1−sk)ak, ​q′(sk)bk ​ ​∞​≤vmax​, ​q′′(sk)bk+q′(sk)ak ​∞​≤amax​,​0≤k≤K0≤k≤K0≤k≤K0≤k≤K​

   $$b(0)=b_0,b(L)=b_L.$$

–

–

–

---

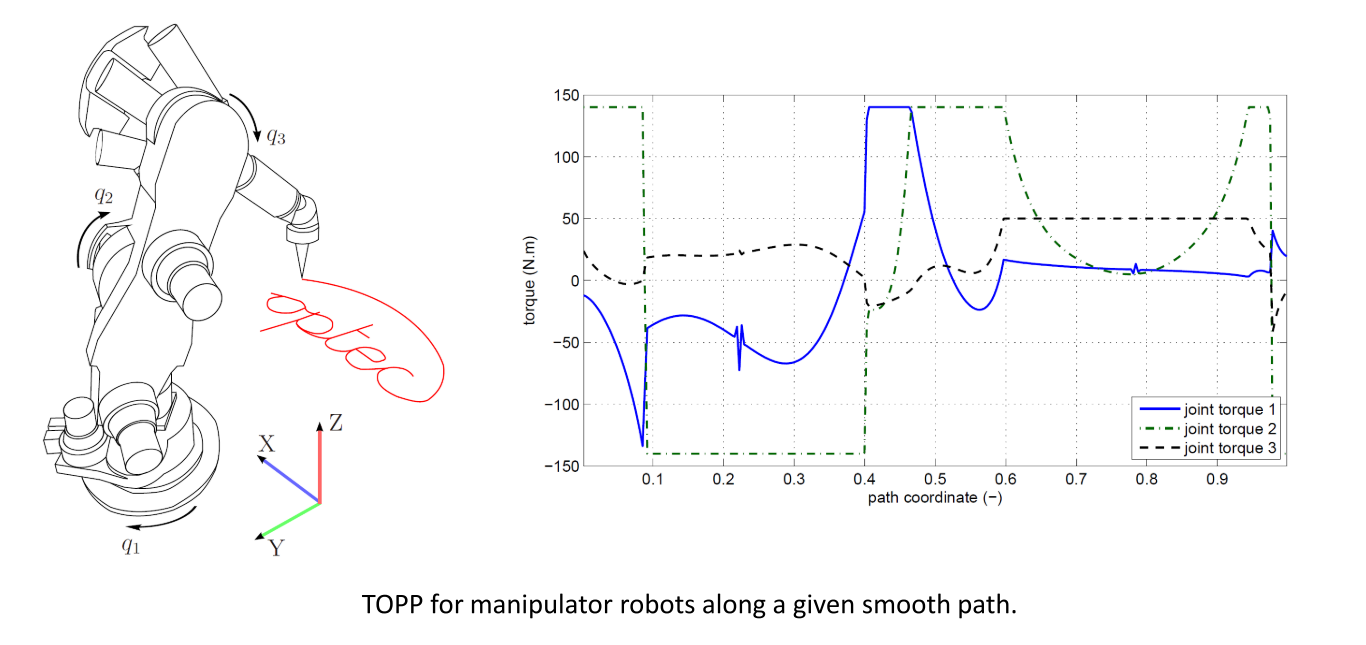
   参考资料：

   1、数值最优化方法（高立 编著）

   2、机器人中的数值优化

---