- 1基于web租车汽车租赁系统设计与实现_汽车租赁系统web
- 2LetCode 127. 单词接龙_python 127. 单词接龙
- 3Git warning:LF will be replaced by CRLF in readme.txt的原因与解决方案
- 4Windows SSH远程连接Linux服务器 无公网IP内网穿透_windows远程连接linux需要ip通隧道吗
- 5【Linux】进程2——管理概念,进程概念
- 6hive的load报错Error: EXECUTION FAILED: Task MOVE error HiveException: [Error 20531] Unable to move sour_unable to move source hdfs
- 7SpringBoot 实战:JUnit5+MockMvc+Mockito 做好单元测试_mockito怎么继承spring_springboot junit5 mocktio
- 8gitee使用之Pull Request_gitee pull request
- 9roboticslibrary的sg
- 10新质生产力赋能金融行业数字化建设方案_金融行业数字化 建设类任务
《Python算法教程》——2.2 渐近记法
赞
踩
本节书摘来自异步社区《Python算法教程》一书中的第2章,第2.2节,作者[挪威]Magnus Lie Hetland(赫特兰), 凌杰 译,更多章节内容可以访问云栖社区“异步社区”公众号查看。
2.2 渐近记法
还记得第1章中那个拿append与insert做对比的例子吗?似乎是出于某种原因,当我们选择将相关元素项添加到list尾端时,其在应对list大小变化时的性能弹性要比在其首端插入要好一些(关于list,读者稍后可以参考黑盒子专栏中的相关内容)。而且,这些内置操作通常还都是用C编写的。如果我们花点时间用纯Python重新实现一下list.append方法,(粗略)估计新版本会比原版本慢50倍左右。并且我们还可以做进一步估计,相较于这个较慢的、纯Python实现的append方法在一台速度非常慢的机器上的表现而言,那个较快的、优化版的insert方法在一台普通计算机上的速度大致要快上1 000倍。那么,如果我们现在将insert版所具有的速度优势设置为50 000一个单位,然后对比这两个实现在插入100 000个数字时的情况,您认为会是什么结果?
从直觉上来看,似乎显然应该是速度快的那个解决方案会胜出。但在这里,其“速度性”只是一个常数单位,而且它的运行时间增长得又比“较慢”的那一版要快一些。就眼前这个例子来说,运行环境较慢的、用纯Python实现的那一版代码完成时间实际上只有其他版本的一半。下面让我们再继续扩大问题的规模,如将数字增加到1 000万个。这时候我们会发现,慢机器上的Python版本(append方法)已经比快机器上的C版本(insert方法)快了近2 000倍1。这中间的区别几乎就相当于其中一个只需运行不到一分钟的时间,而另一个则需要运行近一天半!
这种常数单位上的差距(这通常取决于一些特定事物,如通用编程语言的性能、硬件速度等),以及其在问题规模扩大时运行时间的增长幅度,才是我们研究算法分析时所要关心的重点。也就是说,我们得将焦点集中在大局上——解决问题方法中那些能独立于具体实现的属性。我们希望能排除那些细节干扰,区分出核心问题所在,但要做到这些,我们就需要有一些形式主义方面的东西。


2.2.1 我看不懂这些希腊文
其实自19世纪以来,渐近记法就一直是人们用于分析算法与数据结构的重要工具(当然,在用法上会有一些变化)。其核心思想是想提供一种资源表示形式,主要用于分析某项功能在应对一定规模参数输入时所需要的资源(通常指的是时间,但有时候也包括内存)。例如,我们可以将一个程序所需要的运行时间表示为T (n ) = 2.4n + 7。
紧接着,我们面临的下一个重要问题是:这里用的单位是什么?毕竟乍看之下,无论我们在这里是选择用秒还是毫秒来表示运行时间,或是选择用字节位还是兆字节来表示问题规模,似乎都是无关紧要的。但即便真是这样,这个问题的实际答案也还是多多少少会让您觉得有些意外的,因为它不但无关紧要,而且根本就不会对其最终结果产生任何影响。我们甚至可以用木星年来测算时间,或者用kg(这似乎是用于表示质量的介质单位吧)来表示问题规模,都完全不会有任何问题。因为我们的初衷就是为了能忽略掉这些实现细节上的因素,而渐近记法正好能将它们通通都忽略掉!(虽然我们通常会将问题规模设定成一个正整数。)
最终,我们所获得的运行时间往往取决于某个特定基本操作被执行的次数,而对于问题的规模,我们既可以用待处理项的数量(如待排序的整数数量)来表示,或者在某些情况下,我们也可以用该问题实例在某些既定编码过程中所需要的比特数来表示。

请注意:
通常情况下,我们在对相关问题及其解决方案进行具体编码时所采用的位模式其实对渐近运行时间的影响并不大,但前提是编码方式必须合理。例如,我们应该避免使用一元数字系统(1=1, 2=11, 3=111…)来进行编号。
渐近记法使用的是一组由希腊字母构成的记号体系。这之中最重要的记号(也是我们今后要用到的)分别是O (原本应读作omicron,但我们一般将其读作“大O ”)、Ω(omega)、Θ(theta)。其中,O 记号的定义可以被当作其他两个符号的基础。表达式O (g )代表的是一组与某个函数g (n )有关的函数集合。若要让某函数f (n )属于该集合,该函数须满足以下关系:存在自然数n0和正数c ,对于所有的n ≥n0都有:
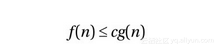
换句话说,即便我们允许对常数c 进行调整(例如让该算法运行在速度不同的机器上),函数g 的增长幅度最终还是会(在n0处)超过f ,如图2-1所示。
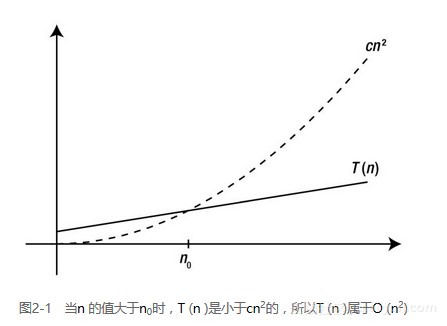
该定义非常简单,也很容易理解,尽管看上去会让人感觉有些陌生。首先是最基本的,O (g )所代表的是一个函数集,它的增长速度不会快于g 。例如,如果函数n2是函数集O (n2)中的一份子,或者如果在集合记法中,n2 ∈ O (n2),我们通常都可以直接认为“n2属于O (n2)”。
但事实上,n2的增长速度本来就不会快过自己,这个推论有点无聊。也许它在以下情况中会更有用一些:无论是2.4n2 + 7还是线性函数n ,我们都可以认为:
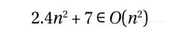
和
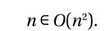
我们在第一个示例中展示的是一个函数在去除旁枝末节之后的表示方式。也就是说,我们可以将该函数中的2.4和7拿掉,直接将其表示为O (n2),这也正是我们所需要的信息。而第二个示例则用于说明:O 记号所能表示的只是一个松散的边界,即O (g )中的任何函数都会比g 更好(增长速度不会比它更快)。
那么,如何将其与我们原先的示例联系起来呢?好吧,联系是这样的:它可以使我们即便是在无法确定所有细节(毕竟,这取决于我们所用的Python版本及其硬件环境)的情况下,依然可以用渐近法来描述相关操作。如对于Python中的list而言,append n 个数字所需要的运行时间约为O (n ),而在其首端insert相同数量的数字需要的时间则约为O (n2)。
而另外两种记法Ω与Θ则可以被视为O 记法的变体。其中,Ω的定义正好与之相反。也就是说,若要让函数f (n )属于Ω(g ),该函数须满足以下关系:存在自然数n0和正数c ,对于所有的n ≥n0都有:
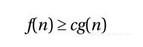
因此,O 记法所代表的其实是所谓的渐近上界,而Ω记法所代表的则是渐近下界。
请注意:
我们前两个渐近记号O 与Ω是相互可逆的,即如果f 属于O (g ),那么g 就属于Ω(f )。在习题1-3中,我们将会要求您证明这个关系。
而Θ记号所代表的集合正好是前面两种记号的交集,即Θ(g ) = O (g ) ∩ Ω(g )。换句话说,若要让某个函数属于Θ(g ),该函数须满足以下条件:存在自然数n0和正数c ,对于所有的n ≥n0都有
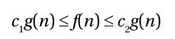
这意味着f 和g 有着相同程度的渐近式增长。例如,当3n2 + 2属于Θ(n2)成立时,同样的关系也可以被写成n2属于Θ(3n2 + 2)。而且,由于Θ记号同时提供了函数的上下界,这使得它成为了我们将来所能用到三个记号中最翔实的一个。
2.2.2 交通规则
虽然这些渐近记号的定义运用起来会有点难,但实际上它们也最大限度地简化了我们所面临的数学问题。我们可以忽略掉乘法或加法运算中的那些常数,以及函数中其他所有“影响较小的部分”,从而让事情得到很大程度的简化。
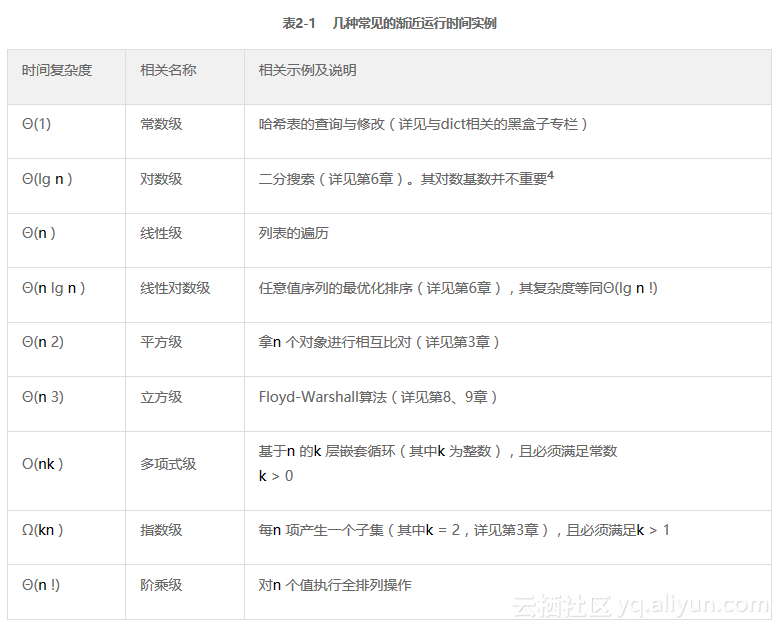
作为玩转这些渐近表达式的第一步,让我们先来看看一些典型的渐近类型,或优先顺序。我们在表2-1中列出了其中一些,内容包括它们的名称,以及对应的典型算法。这些渐近运行时间,有时候也叫作时间复杂度(如果读者对这些数学概念感到陌生,最好参考一下本章后面的“数学快速复习”专栏中的内容)。该表有一个重要特征,它是按照复杂度来排序的,所以它的每一行都要比前一行复杂,也就是如果f 在表中的位置比g 高,那么f 就一定属于O (g )。
请注意:
实际上,该关系更严格来说应该是:f 属于o (g ),这里所用的“小 O ”记号是一种相较于“大 O ”记号来说更严格的符号。直观上,它所表示的不再是谁“不增长得更快”,而是谁“增长得更慢”。形式上,它所表示的是当n 增长到无穷大时,f (n )/g (n )趋向于0的情况,尽管我们完全不必去操心这种情况。
也就是说,任何多项式级(polynomial,这里指任何指数k > 0的项,包括分数)算法的复杂度都要高于对数级(logarithm,包括任何基数),而任何指数级(exponential,包括任何基数k > 1的项)算法复杂度又都要高于多项式级(见习题2-5及2-6)。而且事实上,所有对数级算法都是渐近等效的——因为它们之间往往只相差一个常数因子。然而,多项式级与指数级算法在渐近增长上的差异则要取决于它们各自的指数或基数。所以,显然n5的增长要快于n4,而5n的增长要快于4n 。
该表中主要用的是Θ记法,但其中的多项式级与指数级有点特别,因为它们所处的位置正好分割着易处理问题(“有解”)和难处理问题(“无解”)。对此,我们会在第11章中做详细讨论。就基本而言,一个运行时间为多项式复杂度的算法是可以被接受的,而如果为指数复杂度,则通常是不被接受的。尽管这种说法在实践中未必完全正确(例如,复杂度为Θ(n100)的算法就不见得在实践中会比复杂度为Θ(2n)的更有用一些),但在多数情况下,这样的区分还是有用的5。因为根据这种区分,只要运行时间为O (nk ),并且k >0,我们就可以称其为多项式级,即便这种界限设置得并不严谨。例如,即便二分搜索(详见第6章中黑盒子专栏之二分法)的运行时间为Θ(lg n ),它依然可以被认为是一个“多项式级时间”(或直接简称为“多项式级”)的算法。反过来说,任何一个运行时间为Ω(kn )——甚至是Θ(n !)——的算法也都会被归于指数级。
基于我们目前对这些重要增长形式的优劣顺序所做的基本概述,可以得出两条简单规则。
- 在加法运算中,只以阶数最高的被加数为准。
- 例如,Θ(n2 + n3 + 42) = Θ(n3)。
- 在乘法运算中,常数因子可忽略不计。
- 例如,Θ(4.2n lg n ) = Θ(n lg n )。
通常情况下,我们都会尽可能地让渐近表达式保持简洁,使其可以省去许多不必要的部分。另外,对于O 与Ω,我们通常还有第三条规则,内容如下。
-
保持相关上界或下界的严谨性。
换句话说,我们试图要确保的是最低上限与最高下限。例如,尽管在技术上,n2应该也属于O (n3),但我们通常倾向于其更严格的界限:O (n2)。其实,在多数情况下,最好还是直接采用Θ记号来表示。
在实践中,渐近表达式在算法表达中的作用往往会比其实际值来得更大一些。尽管这在技术上是不准确的(毕竟每个渐近表达式代表的都是一个函数集),但它还是被运用得相当普遍。例如,我们可以直接用Θ(n2) + Θ(n3)来指代f + g 。对于某些(未知)函数f 和g 来说,f 就属于Θ(n2),而g 就属于Θ(n3)。即便我们在因为不能确切了解相关函数而得不到f + g 具体和值的情况下,也可以根据以下两条“福利规则(bonus rules)”,运用渐近表达式来弥补这方面的缺陷。
- Θ(f ) + Θ(g ) = Θ(f + g )
- Θ(f ) · Θ(g ) = Θ(f · g )
在习题2-8中,我们将会要求您证明它们的正确性。
2.2.3 让我们拿渐近性问题练练吧
下面我们来看一些简单的程序,看看您是否能确定它们的渐近运行时间。在这里,我们首先要考虑的是程序在(渐近)运行时间上的变化与问题规模之间的关系,而不是问题实例本身的细节(下一节再来详细讨论问题本身内容会对运行时间产生何种影响)。这意味着对于这些示例来说,if语句并不重要,重要的是循环语句中除纯代码块以外的那部分东西。并且,函数调用本身不会使事情复杂化,这里只会计算该调用本身的复杂度并确保被插入到了对的地方。
请注意:
这里有一种函数调用方案对我们来说会有点困难,即递归函数。对此,我们会在第3、4两章中做详细介绍。
当然,最简单的情况是没有循环。在这种情况下,相关语句是逐条被执行的,因此它们的复杂度是叠加而成的。例如,假设我们已经知道对于一个大小为n 的list来说,调用一次append的复杂度是Θ(1),而调用一次insert(插入位置是0)的复杂度则为Θ(n )。那么请考虑下面两行的程序片段在一个n 大小的list中执行的情况:

我们知道第一行复杂度为常数时间。而当我们执行到第二行时,list的大小已经变成了n + 1。也就是说,第二行现在的复杂度应该为Θ(n + 1),它与Θ(n )是等价的。这样一来,总运行时间就是这两种复杂度之和:Θ(1) + Θ(n ) = Θ(n )。
我们再来考虑一些简单的循环,下面是一个遍历n 个元素序列(也可说是数字序列,如seq=range(n))的循环:6
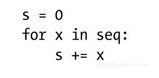
这段代码可以被视为sum函数的一个简单实现:它会对seq进行遍历,并将每个元素值累加到初始变量s上去。也就是说,这里对seq中的n 个元素都执行了常数时间操作(s += x),其运行时间应该是线性的,即Θ(n )。另外值得一提的是,这里还有个常数时间的初始化操作(s = 0),但它被占主导地位的循环操作忽略掉了。
而同样的逻辑也适用于那些“内藏式(camouflaged)”循环,此类循环通常存在于list(或set、dic)等类型的解析式(comprehensions)及生成器表达式(generator expressions)中。例如下面这个列表解析式,它的时间复杂度也是线性级的:
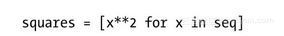
另外那几个内置函数和方法中也存在着一些“隐式(hidden)”循环。它们通常都是一些用于处理容器内各元素的函数和方法,如sum和map。
当我们开始涉及嵌套循环时,事情就会稍微麻烦一点(但也不会麻烦很多)了。例如,我们想要得出seq中所有元素两两之间的乘积之和:
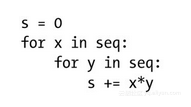
值得注意的是,在这段实现中,每种乘积都被累加了两次(例如,如果42和333都是seq中的元素,那么42333和33342就都会被累加),但这并不会真正影响运行时间(它不过是个常数因子罢了)。
那么,其运行时间究竟是多少呢?基本规则很简单:代码块的复杂度由其先后执行的语句累加而成。而嵌套循环的复杂度则在此基础上成倍增长。理由很简单:由于外循环每执行一次,内循环都要完整执行一遍。在这种情况下,其复杂度就相当于“线性级乘线性级”,即平方级。换句话说,其运行时间应该为Θ(n ·n ) = Θ(n 2)。实际上,这种乘法规则还可以被用于指代更多层嵌套,只需随之增加其乘方数即可(指数值)。例如,三层循环就是Θ(n3),而Θ(n4)则意味着四层,依此类推。
当然,顺序与嵌套这两种情况还可以被混合在一起。接下来,我们来考虑做些轻微地扩展:
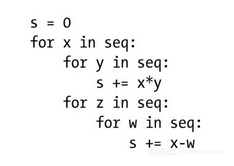
这段代码可能并不清楚我们在这里计算的是什么(当然,我也不清楚),但我们依然可以根据之前那套规则来找出它的运行时间。z循环所运行的是一个线性的数字迭代操作,并且其中还包含着一个线性循环,因此其总复杂度是平方级的,即Θ(n2)。而y循环的复杂度显然是Θ(n )。也就是说,x循环的代码块复杂度应该为Θ(n + n2)。而该代码块在x循环中每执行一次所需要的时间为n ,由此我们可以根据乘法规则推导出该循环的复杂度为Θ(n (n + n2)) = Θ(n2 + n3) = Θ(n3),即立方级。其实我们还可以让推导过程更简单一些,即y循环因占主导的z循环而被忽略掉了,所以其内部代码块应该是平方级运行时间,而“平方级乘线性级”自然就是立方级。
当然,也不是所有循环都需要重复Θ(n )次的。例如,我们有两组序列seq1和seq2,其中seq1中有n 个元素,而seq2中有m 个元素,下面代码的运行时间应该是Θ(nm ):

事实上,内循环在外循环每次迭代中的执行次数也未必非要相同。只不过这样的话,事情就会变得稍微复杂一些,不仅仅是两个迭代次数(就像上述例子中的m 与n )相乘就行了,我们现在必须累计出内循环的迭代次数。读者可以通过以下实例来理解我们所指的是什么。

在这段代码中,语句s += x 被执行了2 + 1 + 3 = 6次。Seq2的长度决定着内循环的运行时间,但由于它是变化的,我们不能直接拿它与外循环的迭代数相乘。下面我们来看一个更具现实意义的例子,重新回到我们先前的那个例子中——算出序列中各元素间的乘积之和:

为了避免对象自身相乘或者同一乘积被累加两次的情况,现在,我们让外循环避开该序列的最后一项,并让内循环的遍历动作从外循环当前位置的后一项开始。尽管在事实上,这种做法没有像看上去那样混乱,但想要找出其复杂度确实需要多费点心思了。而且,这是一个与计数操作(counting)有关的重要案例,属于下一章所要讨论的范围。7
2.2.4 三种重要情况
到目前为止,我们所设想的运行时间都是完全确定的,并且只取决于输入的规模,而与输入的实际内容无关。但这显然不是特别现实。例如,如果想要构建一个排序算法的话,我们或许会这样开始:

也就是在进入实际排序之前先做一个检查,如果目标序列是已排序过的,函数就直接返回。
请注意:
在Python中,如果一个循环没有被break语句提前中止,那么它的可选分支else就会被执行。
这意味着无论我们的主排序算法效率有多低,只要它遇到的是一个已排序的序列,其运行时间就始终是线性级的。而在一般情况下是没有排序算法能达到线性级运行时间的。也就是说,这里所谓的“最好的情况”其实是个异常情况——并且有一定的突然性,我们不能基于这个来预测可靠的运行时间。对于这个难题,我们需要更具体的解决方案。我们可以选择不针对某个一般性问题泛泛而谈,而是限定相关的输入内容,并且我们通常会讨论以下三种重要情况中的一种。
- 最好的情况:当算法遇上最理想输入时的运行时间。例如,当sort_w_chech()检测到输入序列已被排序时,我们所获得的就是最佳情况下的运行时间(线性级时间)。
- 最坏的情况:这通常也是最有用的情况——我们可能会遇上的最糟糕的运行时间之所以说它有用,是因为在通常情况下,我们希望对算法效率做出某些保证,而这就是我们所能给出的最佳保证。
- 平均情况:这是最复杂的一种情况,我们在大部分时间里都会回避这种情况,但对于某些情况,它还是有些用处的。简单而言,就是它是对于按照一定的概率分布的随机输入的期望运行时间值。
在我们工作时所用的许多算法中,这三种情况的复杂度基本上是一致的。当它们不一致时,我们的工作通常会以最坏的情况为准。但除非有明确说明,否则我们通常是不应该指出自己正在研究的是哪一种情况的。事实上,我们也许完全不该将自己局限在所有输入中的某个单一情况上。例如,如果我们想要描述的是sort_w_check()在平均情况下的运行时间,这可行吗?即使我们确实有可能做到,该描述也必然不会太精确。
例如,我们现在所使用的主排序算法(检查之后)是线性对数级的,即其运行时间为Θ(n lg n ),这对于排序算法来说是一个非常典型的情况(而且这事实上也往往是最佳情况了)。这样一来,该算法在最佳情况下的运行时间为Θ(n )(检查结果为已排序序列时),而在最坏情况下的运行时间则为Θ(n lg n )。如果这时我们想对该算法在一般情况下的运行时间做个描述,然而——由于针对的是所有输入——我们无法使用Θ记号,因为没有单一函数能描述该运行时间,不同种类的输入对应着不同的运行时间函数,因而其渐近复杂度也不尽相同。这使我们无法将其概括成一个单一的Θ表达式。
那么该如何解决呢?我们可以放弃Θ记号的“双边界”,而选择直接用上界或下界,即用O 或Ω来描述问题。例如,我们可以说sort_w_check()的运行时间为O(n lg n )。这就同时概括了最好的和最坏的情况。类似地,我们也可以说其运行时间为Ω(n )。但需要提醒的是,对于这些边界,我们应该尽可能设置得严格一些。
请注意:
我们可以使用任何一个渐近记号来描述上述三种情况中的任何一种情况。例如,我们完全可以说sort_w_check()在最坏情况下的运行时间是Ω(n lg n ),或者其最好的情况是O (n )。
2.2.5 实证式算法评估
本书的焦点主要集中在算法设计以及与之相关的算法分析。然而,算法学中还有一门重要学科,其在构建实际系统时所起的作用也是至关重要的,它就是算法工程(algorithm engineering)。这是一门有关如何有效实现相关算法的艺术。从某种程度上来说,算法设计可以被看成一种通过设计高效算法达成低渐近运行时间的方法,而算法工程则侧重于降低渐近复杂度中的隐藏常量。
尽管我们可以专门针对Python给出一些算法工程方面的提示,但很难预计这些调整及黑客技巧能否给我们工作中具体问题的解决带来最佳性能——或者说能否适用于我们所用的硬件环境或Python版本。(这也正是在设计复杂度的渐近表示法时要尽力避免的情况。)并且在某些情况下,我们也没有必要采用这类调整及黑客技巧,因为相对这些手段而言,我们的程序已经够快了。在大多数情况下,我们所能做的最有用的事情也就是试试看而已。如果您认为某种调整手段能对程序有所改善,那就试试吧!实施相关调整并实际验证一下,真的改善了吗?如果这种调整降低了您代码的可读性,而带来的改善却很小,这样做真值得吗?
请注意:
本节所讨论的是程序的评估方案,而不是算法工程本身。对于某些可用于提升Python程序速度的技巧,读者可以参考附录A中的相关内容。
虽然理论上确实存在一种叫作算法评估(experimental algorithmics,即与算法实践评估及其具体实现相关的内容)的东西,但它不在本书的讨论范围内。我们接下来要介绍的一些实践性提示也与此相去甚远。
提示1:
只要有可能,就不必去担心。
对渐近复杂度的担心可能很重要。有时候,它就相当于解决方案与非解决方案之间在实践中的不同之处。然而,运行时间当中的常数因子却往往没有那么重要。不妨试试先简单地实现一下您的程序,然后看看它是否足够好。事实上,我们甚至可以先试试朴素算法(naïve algorithm),引用编程大师Ken Thompson的话说:“当没有把握的时候,就用蛮力试试。”在算法学中,所谓的蛮力往往指的就是简单地将每种可能的解决方案都试一遍,运行时间可能很糟糕。只要它工作了,就是有用的了。
提示2:
请用timeit模块来进行计时。
timeit模块本身就是为执行相对可靠的计时操作而设计的。尽管要得到真正确切的结论(如发表一篇学术论文)需要做大量的工作,但timeit至少可以帮助我们简单地得到“实践中足够好”的计时操作。例如:

当然,您看到的时间值肯定不会与我完全相同。另外,如果想对某一函数进行计时(如用来封装您代码的某个测试函数),我们也可以更简单地通过命令行环境中的-m开关来调用timeit模块:

但当您调用timeit模块时,有一件事需要特别注意:避免一些因重复执行带来的副作用。因为timeit函数会通过多次运行相关代码的方式来提高计时精度,所以,如果早先执行的操作会影响其后面的运行,我们可能就遇上麻烦了。例如,如果我们要对mylist.sort()这样的函数进行计时,该列表只是在首次运行中得到了排序,而在该语句的其他数千次运行中,它都是一个已排序列表了,这显然会使我们的计时结果偏低。相同道理也适用于所有涉及迭代式(generator)或迭代器(iterator)的这类穷举操作。关于该模块的更多细节及其工作方式,读者可以自行参考标准库文档8。
提示3:
请使用profiler找出瓶颈。
在实践过程中,我们经常会去猜测自己代码中需要优化的是哪一部分,而这种猜测往往又都是错的。所以,与其这样胡乱猜测,不如让profiler来替我们找出来。Python语言中就自带了少量的profiler变体,但我们还是建议您使用cProfile模块,它使用起来与timeit一样简单,但能给出关于执行时间都花在哪里的更为详细的信息。例如,我们的主函数是main(),那么我们就可以像下面这样,通过profiler来运行程序:

这样就应该能打印出程序中各函数的计时结果。而如果cProfile模块在您的系统中不可用的话,我们用profile来代替它。同样,关于这方面的更多信息,读者可以自行查看相关库参考文件。而如果我们对实现细节不感兴趣,只是想对自己针对某既定问题实例提出的算法进行实证研究,那么标准库中的trace模块是个有用的选择——它可以对程序中各语句的执行次数进行计数操作。您甚至可以通过使用例如Python Call Graph9的工具,可视化地看到代码的调用情况。
提示4:
绘制出结果。
在需要理清某些事情的时候,可视化往往可以成为一种非常好的工具。在性能图形化方面,我们有两种常见的绘图,一种是反映问题规模与运行时间关系的图表10,另一种是如图2-2展示的相关运行时间的详细分布情况的盒形图。另外,在Python中,matplotlib是一个非常不错的绘制工具包(可以去http://matplotlib.org下载)。
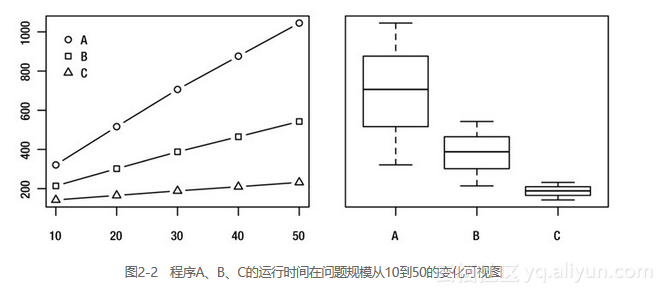
提示5:
在根据计时比对结果做出判断时要小心仔细。
这条提示有点模糊不清,这是因为在我们依据计时实验结果对“哪一种实现更好”的问题做判断时会遇到许多陷阱。首先,我们会观察到一些随机变量所带来的差异。例如,您使用了timeit这类工具的话,这样的风险就会少一些,因为这类工具是通过相关语句的多次重复执行来进行计时的(甚至我们可能会多次重复运行整个实验,然后将最佳的那一次运行保存下来)。但即便如此,随机变量依旧还是存在的。因此,如果这两种实现方式之间的差异大不过我们对这些随机因素的预期,我们就无法真正确定它们之间的差距在哪里。(其实,我们甚至也无法判断它们之间是否真的存在差距。)
请注意:
如果我们非做出判断不可的话,也可以用统计学中的假设性测试技术来解决问题。但就其实际作用而言,如果我们无法确定其间的差距究竟有多小,或许我们选择哪一种实现根本就无关紧要,所以您可以根据自己的喜好来。
但如果我们想要比较两个以上实现的话,问题就复杂了。其成对比较的操作数会随版本数呈平方级增长(关于这点,我们将会在第3章中做出解释),但其大幅增长的机会往往至少要存在于两个版本之间的差异当中,尽管这也仅仅是个机会。(这也就是所谓的多重比较问题。)尽管该类问题有现成的统计学解决方案,但最简单易行的解决方法还是对这两种实现再进行一次验证,甚至是多次验证,看看它们是否仍有什么不同。
其次,这种对平均值所进行的比较本身也存在一些问题。最起码,我们应该坚持对其实际计时结果来进行平均值比较。在实践中,我们在对各程序执行计时实验时需要得到更有意义的数字。对此,我们通常的做法是通过将每个程序的运行时间标准化,然后让它们分别去除以某种简单的标准算法的运行时间。这种做法的确能发挥一定的作用,但在某些情况下,它也会让我们获得的结果失去意义。关于这些方面,读者可以参考Fleming与Wallace在他们的论文《How not to lie with statistics: The correct way to summarize benchmark results》11中所做的一些指导性建议。而对于一些其他方面的观点,读者也可以阅读Bast和Weber所著的《Don’t compare averages》一文,或者Citron等人最近发表的论文《The harmonic or geometric mean: does it really matter?》。
再次,我们的判断也可能不具有普遍性。例如,几个相互类似的实验运行在其他问题实例和硬件环境上时,可能会产生截然不同的结果。因此,如果想让其他人去解释或重现您的实验,提供完备的执行记录文档是非常重要的。
提示6:
通过相关实验对渐近时间做出判断的时候要小心仔细。
如果我们想针对某个算法行为的渐近性做出某种判断,就必须像本章之前所描述的那样,对其进行详细分析。做实验确实能给我们带来一些提示,但其作用终究是有局限性的。而渐近性所代表的是任意规模下的数据处理情况。但从另一角度来说,除非我们从事的是纯计算机科学理论工作,否则我们进行渐近性分析的目的也主要是为了实现算法,以及在实际问题中运行算法时,能对该算法的行为做出某些描述,这意味着它与做实验还是应该有一定关联性的。
设想一下,如果您直觉上认为一个算法所拥有的时间复杂度是平方级的,却又无法证明自己的判断。这时候,您会通过实验来支持自己的论点吗?虽然我们之前曾解释过,(算法工程与)实验关注的主要是常数因子,但这也是有办法解决的。主要问题是您的判断本身是否真的具备可测试性(通过实验方式)。例如,如果您只是声称某一算法的运行时间为O (n2),那恐怕确实没有数据可以证实或反证这一说法。然而,如果我们能让这一说法变得更具体一些,使其具备可测试性。例如,我们可以先根据一些初步结果设定一个时间:0.24n2 + 0.1n + 0.03秒,然后确信相关运行时间绝不会超过这个设定。或许还可以更实际点,我们的设想也可以是某既定操作被执行的次数,您可以通过trace模块来完成这部分测试。那么,这就是一个可测试(或者说更具体、可反证)的假设。如果我们进行了大量的实验,却找不到任何反证,那么它就在一定程度上支持了我们的假设。同时,它也间接支持了我们认为相关算法复杂度为O (n2)的判断。



