人工智能 A*算法 八数码 Java_人工智能八数码问题java

一、问题描述

八数码问题是在3×3的九宫格，分布数字1～8。其中有一个空格，这里我们记为0。0可以移动，给定初始状态，问如何移动，实现从初始状态到目标状态的转变。

二、解决方法

1、定义状态空间

2、确定一组操作

0有四种移动操作：上、下、左、右移动，有一定的限制。
处于第0行时就不能上移，
处于第0列时就不能左移，
处于第2行时就不能下移，
处于第2列时就不能右移

3、A*算法简介（可跳过）

A* 算法是一种搜索，一种启(xuan)发(xue)式搜索。说到搜索，还是得先说最基本的搜索：深搜和广搜。深搜的好处是时间快，但是不一定能求出最优解；而广搜确实可以求出最优解，但由于广搜是一层层搜下去的，必须扩展每一个点，所以时间效率和空间效率都不高。而A*算法恰可以解决这两个缺点：既有极大概率求出最优解，又可以减少冗余的时间。
详情参考原文：https://blog.csdn.net/stevensonson/article/details/79393052
其特点在于对估价函数的定义上。对于一般的启发式图搜索，总是选择估价函数f值最小的节点作为扩展节点。
f(n) = d(n) + h(n)
其中：
d(n) 是在状态空间中从初始节点到n节点的实际代价
h(n) 是从n到目标节点最佳路径的估计代价
f(n) 是从初始点经由节点n到目标点的估价函数

4、算法具体实现（重要）

(1).设计估价函数f(n)

d(n)为从初始状态到当前状态移动了多少步（即节点深度）
h(n)为当前状态和目标状态数字不一样的个数

(2).流程图

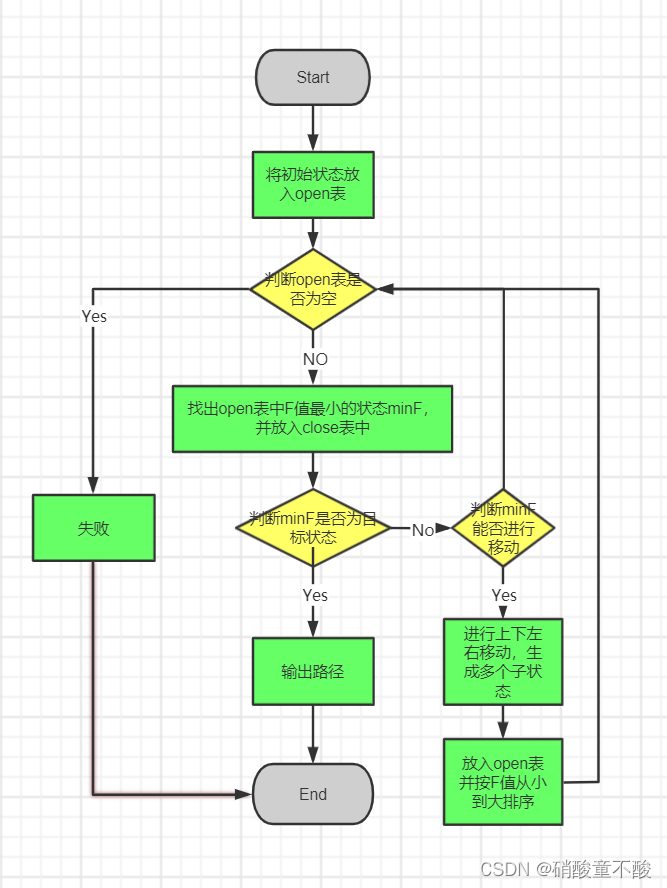
(3).搜索过程

open表存放已经生成而未考察的节点
close表存放已经访问过的节点

每次从open表中取出估计值f最小的的节点，并把该节点放到close表，如果和目标状态相同，退出循环。否则进行移动操作生成多个子状态，对每个子状态进行判断：
1.如果既不在open表中又不在close表，则计算该子状态估值函数的值，并将子状态放入open表中
2.如果在close表中，意味着相同的状态已经访问过，为避免重复，跳过
3.如果在open表中，就比较两者的实际代价的d(n),看谁移动的步数更少，用小的去覆盖大的
全部判断完之后，对open表按照估计函数值从小到大排序，重复此操作，直到找到目标状态。

三、代码实现

原文参考：https://blog.csdn.net/qq_41706670/article/details/90142802?spm=1001.2014.3001.5502

1.部分关键代码

成员变量：

	int[] number = new int[9];//存放状态
    int f;//估计函数
    int d;//实际代价，走到当前状态的步数
    int h;//估计代价，当前状态和目标状态有多少个数不同
    EightNum parent;//记录当前状态的父状态
    ArrayList<EightNum> result = new ArrayList<>();//保存最终路径
1
2
3
4
5
6

operation方法实现对子状态的判断和处理
1.如果既不在open表中又不在close表，则计算该子状态估值函数值f(n)，并将子状态放入open表中
2.如果在close表中，意味着相同的状态已经访问过，为避免重复，跳过
3.如果在open表中，就比较两者的实际代价的d(n),看谁移动的步数更少，用小的去覆盖大的

public void operation(ArrayList<EightNum> open, ArrayList<EightNum> close, EightNum minF, EightNum target) {
        if (this.isContains(close) == -1) {//判断是否在close表
            int position = this.isContains(open);//判断是否在open表，存在就返回其在open表中的位置
            if (position == -1) {//不在open表中
                this.parent = minF;//链接，设置minF为该子状态的父状态
                this.init(target);//计算估计函数
                open.add(this);//放入open表
            }
            else {//在open表中
                if (this.d < open.get(position).d) {//根据移动步数，小的覆盖大的
                    open.remove(position);
                    this.parent = parent;
                    this.init(target);
                    open.add(this);
                }
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

主函数：

public static void main(String[] args) {
        //open表存放已经生成而未考察的节点
        ArrayList<EightNum> open = new ArrayList<>();
        //close表存放已经访问过的节点
        ArrayList<EightNum> close = new ArrayList<>();
        EightNum start = new EightNum();//存放初始状态
        EightNum target = new EightNum();//存放目标状态
        int[] sNum = {2,1,3,8,0,4,6,7,5};//初始状态
        int[] tNum = {1,2,3,8,0,4,7,6,5};//目标状态
        start.number = sNum;
        target.number = tNum;
        System.out.println("初始状态：");
        start.output();
        System.out.println("目标状态：");
        target.output();
        if(start.isSolvable(target)){//判断从初始状态到目标状态是否可达
            start.init(target);//初始化，计算估价函数
            open.add(start);//加入open表
            while(!open.isEmpty()){//判断open表是否为空
                Collections.sort(open);//根据F值对open表进行从小到大排序
                EightNum minF = open.get(0);//取出最小的，也就是第0个
                open.remove(0);//从open表移出
                close.add(minF);//放入close表
                if(minF.isTarget(target)){//判断是否为目标状态
                    minF.printRoute();//输出完整路径
                    break;
                }
                int move;
                //由minF状态进行扩展并加入到open表
                //0的位置上移之后的状态不在close和open中设定minF为父状态，并初始化f的估值函数
                if(minF.isMoveUp()){
                    move = 0;
                    EightNum up = minF.moveUp(move);
                    up.operation(open,close,minF,target);
                }
                //0的位置下移之后状态不在close和open中设定minF为其父状态，并初始化f(n)估值函数
                if (minF.isMoveDown()) {
                    move = 1;
                    EightNum down = minF.moveUp(move);
                    down.operation(open, close, minF, target);
                }
                //0的位置左移之后状态不在close和open中设定minF为其父状态，并初始化f(n)估值函数
                if (minF.isMoveLeft()) {
                    move = 2;
                    EightNum left = minF.moveUp(move);
                    left.operation(open, close, minF, target);
                }
                //0的位置右移之后状态不在close和open中设定minF为其父状态，并初始化f(n)估值函数
                if (minF.isMoveRight()) {
                    move = 3;
                    EightNum right = minF.moveUp(move);
                    right.operation(open, close, minF, target);
                }
            }
        }
        else
            System.out.println("目标状态不可达");
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

2.全部代码

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;

public class EightNum implements Comparable {
    int[] number = new int[9];
    int f;//估计函数
    int d;//实际代价，走到当前状态的步数
    int h;//估计代价，当前状态和目标状态有多少个数不同
    EightNum parent;//记录当前状态的父状态
    ArrayList<EightNum> result = new ArrayList<>();//保存最终路径

    //目标状态的可达性判断，通过判断两个状态的逆序数是否相同来判断
    //注意：需要排除0
    public boolean isSolvable(EightNum target) {
        int num = 0;
        for (int i = 1; i < 9; i++) {
            for (int j = 0; j < i; j++) {
                if (number[j] > number[i] && number[j] != 0 && number[i] != 0)
                    num++;
                if (target.number[j] > target.number[i] && target.number[j] != 0 && number[i] != 0)
                    num++;
            }
        }
        //如果能被2整除，说明同奇或者同偶
        return num % 2 == 0;
    }
    //对状态进行初始化，计算估价函数
    public void init(EightNum target) {
        int h = 0;
        for (int i = 0; i < 9; i++) {
            if (number[i] != target.number[i])
                h++;//记录当前状态和目标状态的差距
        }
        this.h = h;
        if (this.parent == null)
            this.d = 0;
        else
            this.d = this.parent.d + 1;//实际代价
        this.f = this.d + this.h;//返回当前状态的估计值
    }
    public boolean isTarget(EightNum target) {
        //判断当前状态是否是目标状态
        return Arrays.equals(number, target.number);
    }
    //重写compareTo
    @Override
    public int compareTo(Object o) {
        EightNum e = (EightNum) o;
        return this.f - e.f;
    }
    //获取0的位置
    public int getZeroPosition() {
        int position = -1;
        for (int i = 0; i < 9; i++) {
            if (this.number[i] == 0) {
                position = i;
            }
        }
        return position;
    }
    //判断该状态是否在表中，如果在。就返回位置
    public int isContains(ArrayList<EightNum> arrayList) {
        for (int i = 0; i < arrayList.size(); i++) {
            if (Arrays.equals(arrayList.get(i).number, number))
                return i;
        }
        return -1;
    }
    //判断能否上移
    public boolean isMoveUp() {
        int position = getZeroPosition();
        return position > 2;
    }
    //判断能否下移
    public boolean isMoveDown() {
        int position = getZeroPosition();
        return position < 6;
    }
    //判断能否左移
    public boolean isMoveLeft() {
        int position = getZeroPosition();
        return (position) % 3 != 0;
    }
    //判断能否右移
    public boolean isMoveRight() {
        int position = getZeroPosition();
        return (position) % 3 != 2;
    }
    //实现移动
    public EightNum moveUp(int move) {
        EightNum newState = new EightNum();//创建一个对象
        newState.number = number.clone();//将当前状态赋值给新创建的对象
        int zero = getZeroPosition();//记录0的位置
        int position = 0;//记录移动后的位置
        switch (move) {
            case 0://上移
                position = zero - 3;
                break;
            case 1://下移
                position = zero + 3;
                break;
            case 2://左移
                position = zero - 1;
                break;
            case 3://右移
                position = zero + 1;
                break;
        }
        newState.number[zero] = number[position];
        newState.number[position] = 0;
        return newState;
    }
    //输出单个状态
    public void output() {
        for (int i = 0; i < 9; i++) {
            if (i % 3 == 2)
                System.out.println(this.number[i]);
            else
                System.out.print(this.number[i] + " ");
        }
    }
    //输出路径
    public void printRoute() {
        EightNum temp;
        int count = -1;
        temp = this;
        System.out.println("----开始移动----");
        //路径用链表的方式存放，所以是逆序的
        //所以把他放到result表中，方便输出
        while (temp != null) {
            result.add(temp);
            temp = temp.parent;
            count++;
        }
        for (int i = result.size() - 1; i >= 0; i--) {
            System.out.println("第"+ (count-i) +"步:");
            result.get(i).output();
        }
        System.out.println("最小移动步数:" + count);
    }

    public void operation(ArrayList<EightNum> open, ArrayList<EightNum> close, EightNum minF, EightNum target) {
        if (this.isContains(close) == -1) {//判断是否在close表
            int position = this.isContains(open);//判断是否在open表，存在就返回其在open表中的位置
            if (position == -1) {//不在open表中
                this.parent = minF;//链接，设置minF为该子状态的父状态
                this.init(target);//计算估计函数
                open.add(this);//放入open表
            }
            else {//在open表中
                if (this.d < open.get(position).d) {//根据移动步数，小的覆盖大的
                    open.remove(position);
                    this.parent = minF;
                    this.init(target);
                    open.add(this);
                }
            }
        }
    }

    public static void main(String[] args) {
        //open表存放已经生成而未考察的节点
        ArrayList<EightNum> open = new ArrayList<>();
        //close表存放已经访问过的节点
        ArrayList<EightNum> close = new ArrayList<>();
        EightNum start = new EightNum();//存放初始状态
        EightNum target = new EightNum();//存放目标状态
        int[] sNum = {2,1,3,8,0,4,6,7,5};//初始状态
        int[] tNum = {1,2,3,8,0,4,7,6,5};//目标状态
        start.number = sNum;
        target.number = tNum;
        System.out.println("初始状态：");
        start.output();
        System.out.println("目标状态：");
        target.output();
        if(start.isSolvable(target)){//判断从初始状态到目标状态是否可达
            start.init(target);//初始化，计算估价函数
            open.add(start);//加入open表
            while(!open.isEmpty()){//判断open表是否为空
                Collections.sort(open);//根据F值对open表进行从小到大排序
                EightNum minF = open.get(0);//取出最小的，也就是第0个
                open.remove(0);//从open表移出
                close.add(minF);//放入close表
                if(minF.isTarget(target)){//判断是否为目标状态
                    minF.printRoute();//输出完整路径
                    break;
                }
                int move;
                //由minF状态进行扩展并加入到open表
                //0的位置上移之后的状态不在close和open中设定minF为父状态，并初始化f的估值函数
                if(minF.isMoveUp()){
                    move = 0;
                    EightNum up = minF.moveUp(move);
                    up.operation(open,close,minF,target);
                }
                //0的位置下移之后状态不在close和open中设定minF为其父状态，并初始化f(n)估值函数
                if (minF.isMoveDown()) {
                    move = 1;
                    EightNum down = minF.moveUp(move);
                    down.operation(open, close, minF, target);
                }
                //0的位置左移之后状态不在close和open中设定minF为其父状态，并初始化f(n)估值函数
                if (minF.isMoveLeft()) {
                    move = 2;
                    EightNum left = minF.moveUp(move);
                    left.operation(open, close, minF, target);
                }
                //0的位置右移之后状态不在close和open中设定minF为其父状态，并初始化f(n)估值函数
                if (minF.isMoveRight()) {
                    move = 3;
                    EightNum right = minF.moveUp(move);
                    right.operation(open, close, minF, target);
                }
            }
        }
        else
            System.out.println("目标状态不可达");
    }
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222

四、运行结果

---

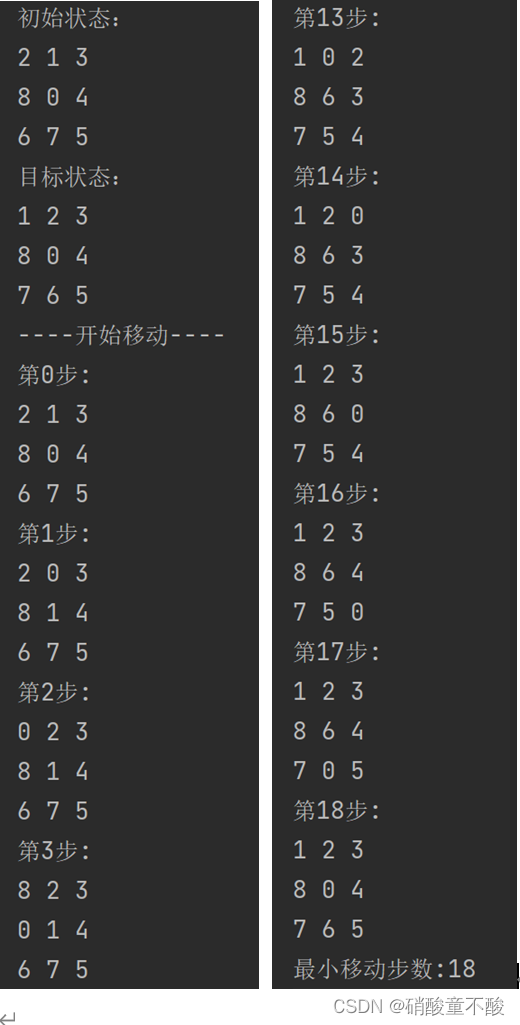
总结

给自己复习看的，因为刚开始网上找了一堆愣是看不明白，所以打算自己写一遍，也算是加深印象，说多了都是泪。
同时希望可以帮助到需要帮助的人。有问题可以留言，不保证能解决，我老菜了。