第4讲 -- 线性调频连续波LFMCW测量原理：测距、测速、测角_调频连续波测距

一、静止目标

1.1 测距原理

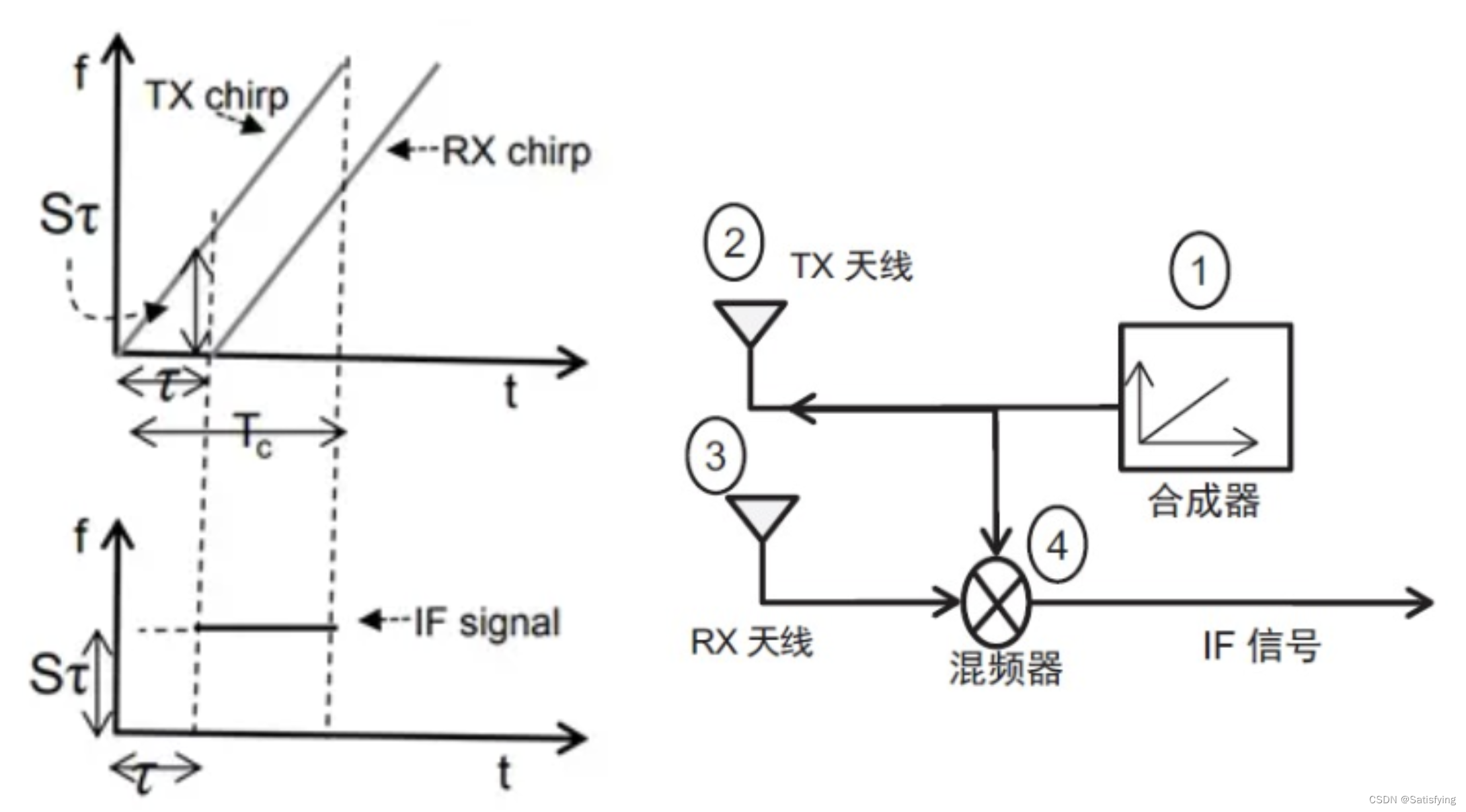
目标静止时，目标和雷达之间没有多普勒频偏，回波信号和发射信号之间只是存在一个时延，因此回波信号波形图是发射信号波形图沿时间轴的左右平移，如下左图。假设静止目标距雷达的距离为R，电磁波在空气中的传播速度为c，则接收信号和发射信号之间存在固定的信号延迟$\tau =\frac{2R}{c}$，因此理想情况下，回波信号模型可表示为：
$$s_r(t)=KAcos(2\pi (f_0(t-\tau )+\frac{S(t-\tau {)}^2}{2})+{\varphi }_0))$$
回波信号相位为：
$$p_r(t)=2\pi (f_0(t-\tau )+\frac{S(t-\tau {)}^2}{2})+{\varphi }_0)$$
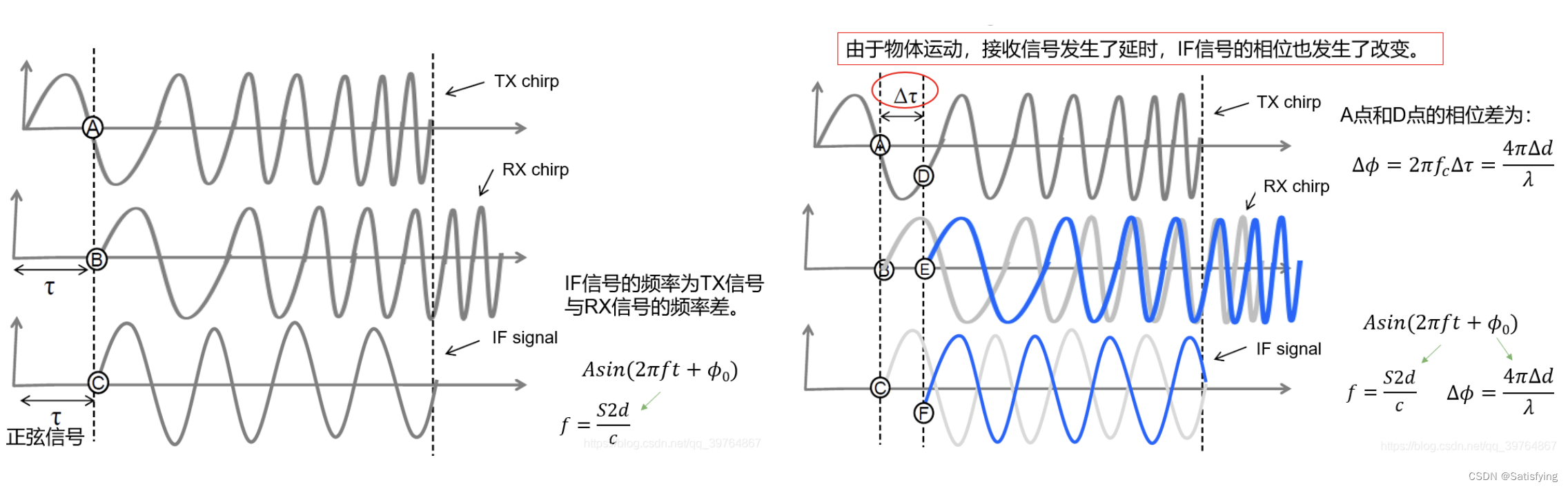
如下中图，将接收到的回波信号和发射信号经过混频器，再经过一个低通滤波器就可以得到一个单一频率的正弦波信号，叫做差频信号，如下左图中IF signal。差频信号的相位为：
$$p_t(t)-p_r(t)=2\pi f_0\tau +2\pi S\tau t-\pi S{\tau }^2$$
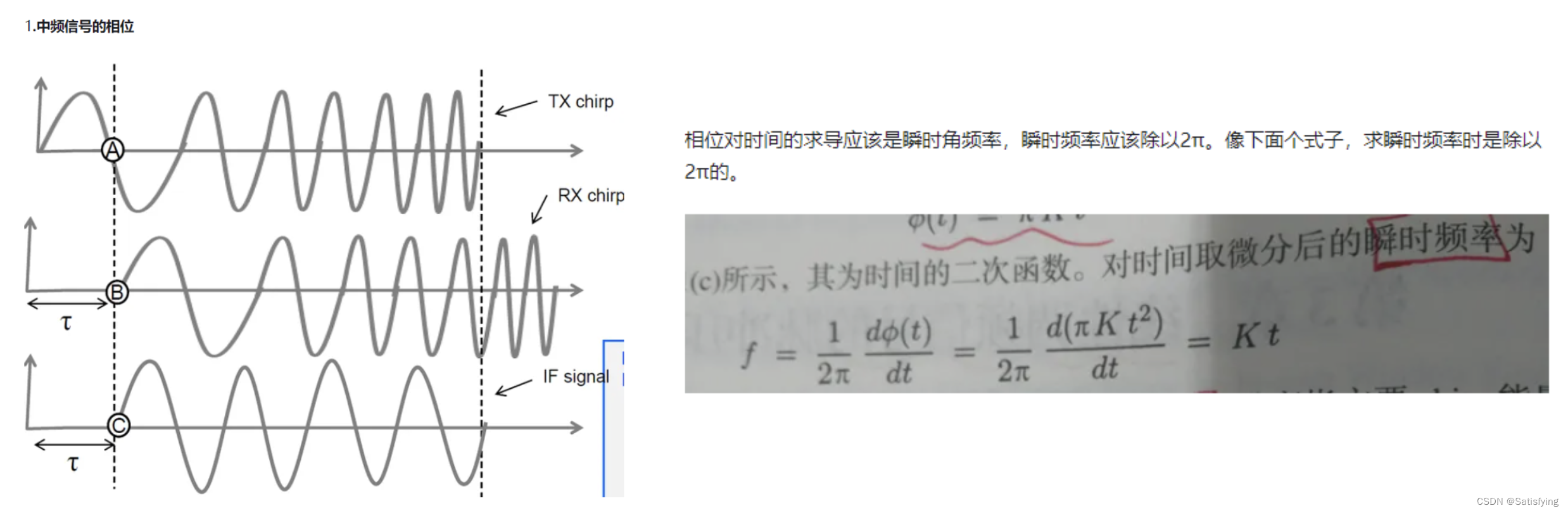
相位对时间求导为瞬时角频率，除以2pi就是瞬时频率，因此差频信号的频率为：
$$f_m=S\tau =\frac{B}{T}\frac{2R}{c}=\frac{2BR}{cT}$$
因此，可以从频谱图中得到谱峰值对应的频率fm，再倒推得到目标距离R为：
$$R=\frac{cT{f}_m}{2B}$$

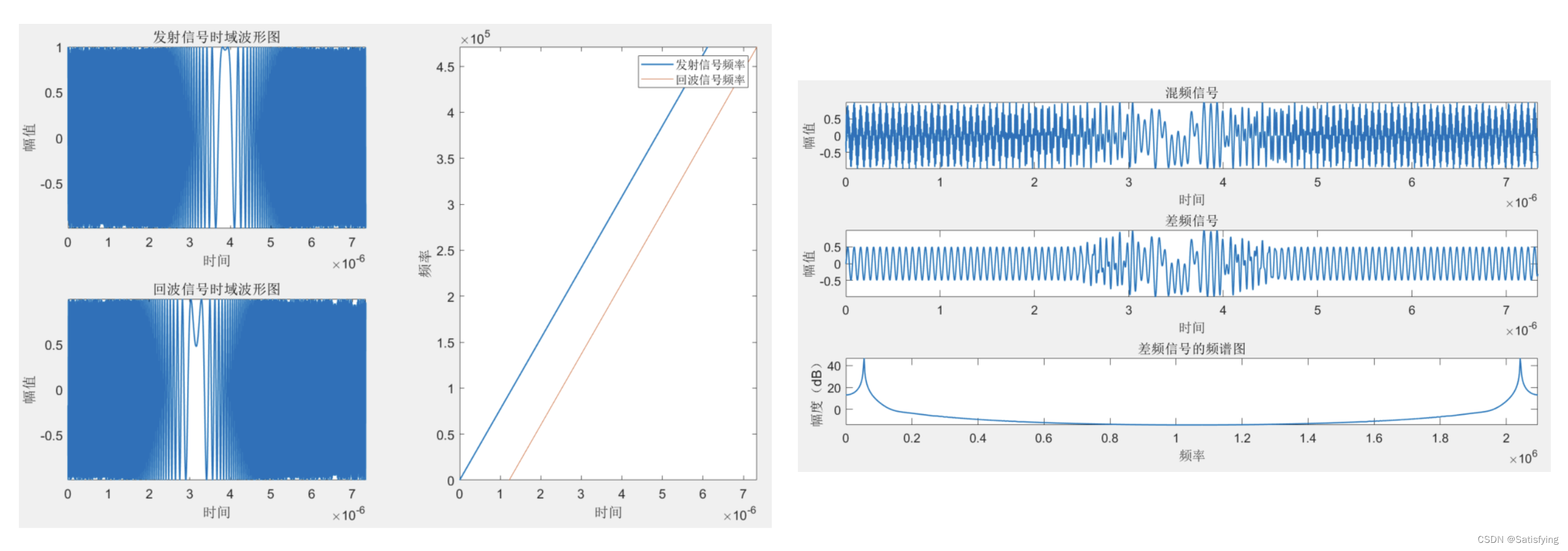
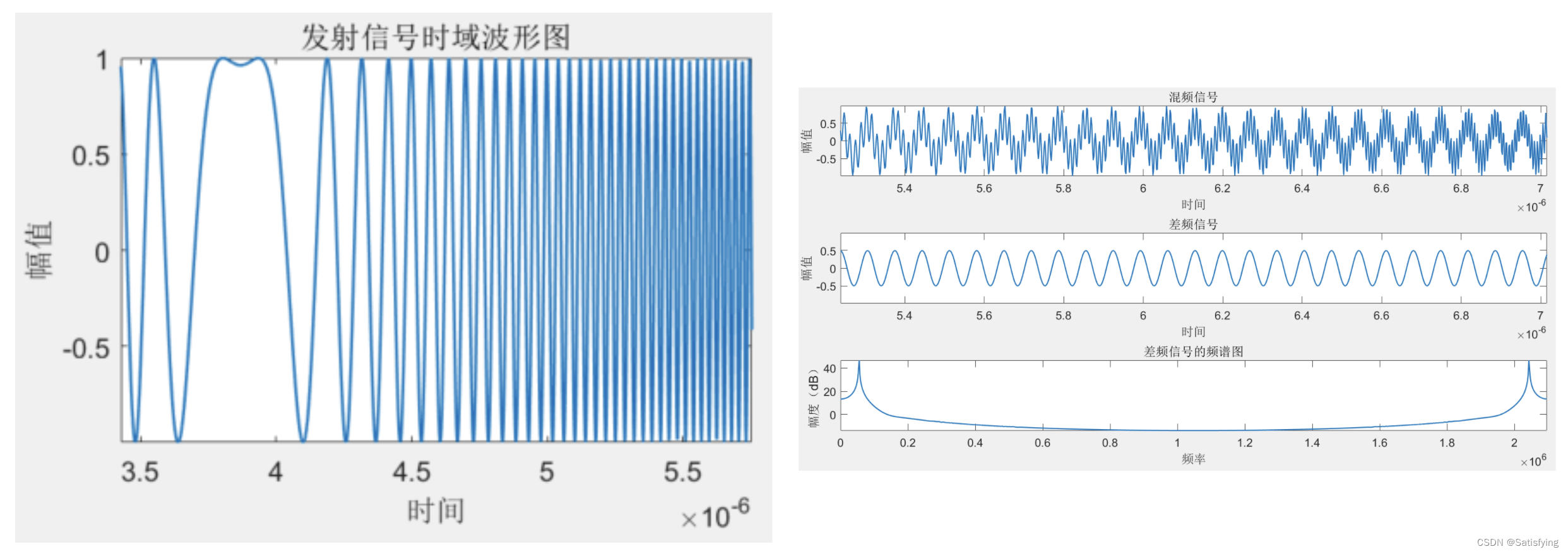
1.2 Matlab仿真

clear; clc; close all; warning off;

%% 参数设置
maxR = 200;  % 最大探测距离
rangeRes = 1;  % 距离分辨率
maxV = 70;  % 最大检测目标的速度
fc = 77e9;  % 工作频率（载频）
c = 3e8;  % 光速
r0 = 90;  % 目标距离设置 (max = 200m)
v0 = 10;  % 目标速度设置 (min =-70m/s, max=70m/s)

%% 产生信号
B = c / (2 * rangeRes);  % 扫频带宽（B = 150MHz）
Tchirp = 5.5 * 2 * maxR / c;  % 扫频时间 (x-axis), 5.5= sweep time should be at least 5 o 6 times the round trip time
S = B / Tchirp;  % 调频斜率
phi = 0;  % 初相位
N_chrip = 128;  % chirp数量           
Ns = 4096;  % ADC采样点数
t = linspace(0, N_chrip * Tchirp, N_chrip * Ns);  % 发射信号和接收信号的采样时间
ft = fc .* t + (S .* t.^2) ./ 2;
Tx = cos(2 * pi .* ft + phi);  % 发射信号
tau = Tchirp / 6;  % 时延
fr = fc .* (t - tau) + S .* (t - tau).^2;  % 回波信号频率
Rx = cos(2 * pi .* fr / 2 + phi);  % 回波信号

%% 经过混频器
Mix = Tx .* Rx;

%% 混频经过低通滤波器
fpass = 30e5;  % 截止频率fpass=30MHz
fs_lpf = 120e6;  % 采样频率fs=120MHz
Mix_filtered = lowpass(Mix(1:Ns), fpass, fs_lpf); 

%% 计算差频
N_fft = 1024;
f = (0 : N_fft - 1) / 2 * Ns;
Mix_filtered_fft = db(abs(fft(Mix_filtered, N_fft)));

%% 作图
figure(1); clf;
sp1 = subplot(2, 2, 1); plot(t(1:Ns), Tx(1:Ns), 'linewidth', 1.2); axis('tight');
xlabel('时间'); ylabel('幅值'); title('发射信号时域波形图'); set(gca, 'fontsize', 12);
sp3 = subplot(2, 2, 3); plot(t(1:Ns), Rx(1:Ns), 'linewidth', 1.2); axis('tight'); 
xlabel('时间'); ylabel('幅值'); title('回波信号时域波形图'); set(gca, 'fontsize', 12);
subplot(2, 2, [2, 4]); plot(t(1:Ns), ft(1:Ns), 'linewidth', 1.2); hold on;
plot(t(1:Ns), fr(1:Ns)); hold off; axis('tight'); ylim([0, max(fr(1:Ns))]);
xlabel('时间'); ylabel('频率'); legend('发射信号频率', '回波信号频率'); set(gca, 'fontsize', 12);
linkaxes([sp1, sp3], 'x'); 
figure(2); clf;
sp11 = subplot(3, 1, 1); plot(t(1:Ns), Mix(1:Ns), 'linewidth', 1.2); axis('tight');
xlabel('时间'); ylabel('幅值'); title('混频信号'); set(gca, 'fontsize', 12);
sp22 = subplot(3, 1, 2); plot(t(1:Ns), Mix_filtered(1:Ns), 'linewidth', 1.2); axis('tight'); 
xlabel('时间'); ylabel('幅值'); title('差频信号'); set(gca, 'fontsize', 12);
subplot(3, 1, 3); plot(f, Mix_filtered_fft, 'linewidth', 1.2); axis('tight'); 
xlabel('频率'); ylabel('幅度（dB）'); title('差频信号的频谱图'); set(gca, 'fontsize', 12);
linkaxes([sp11, sp22], 'x'); 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

运行结果：

二、运动目标

2.1 测距原理

当目标相对雷达有径向运动时，由于多普勒效应回波信号和发射信号之间存在频率偏移fd，回波信号波形图相对发射信号波形图不仅有左右平移，还有上下平移，如下图：

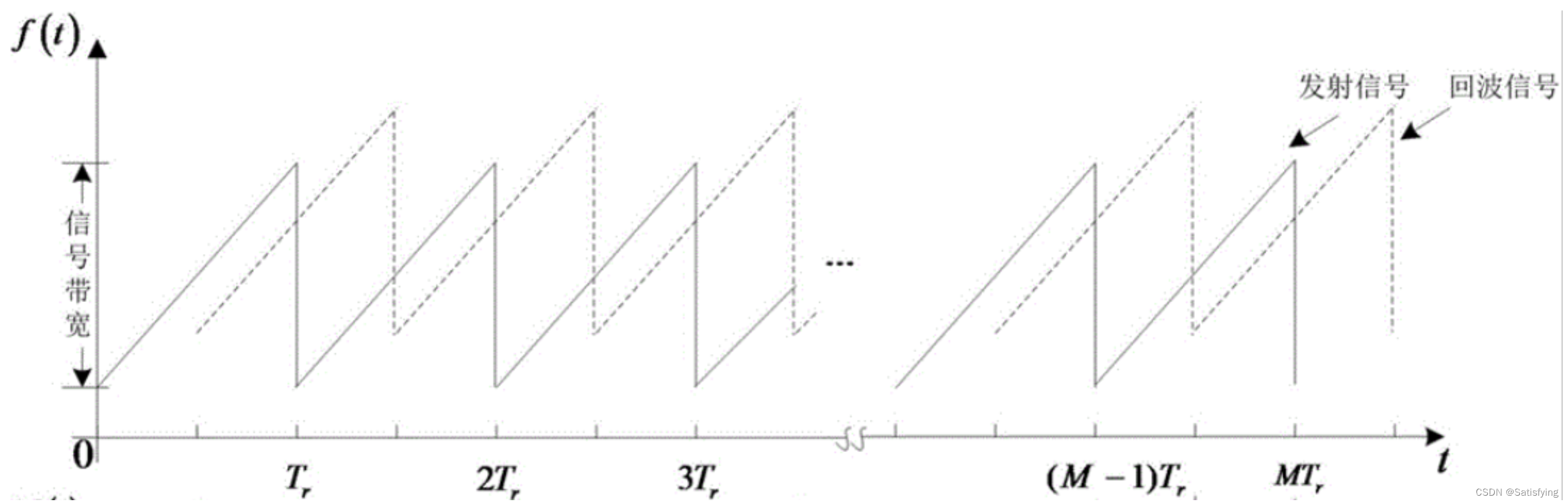
假设在电磁波区域内，有一个目标在t0时刻距离雷达的距离为R0，并以径向距离vr远离天线，那么回波信号依然可表示为：
$$s_r(t)=KAcos(2\pi (f_0(t-\tau )+\frac{S(t-\tau {)}^2}{2})+{\varphi }_0))$$
和静止目标不同的是，运动目标的时延不同，记为${\tau }_t=\frac{2R^{\prime }}{c}=\frac{2(R_0+v_{r}t)}{c}$，代入差频信号相位有：
p t ( t ) − p r ( t ) = 2 π f 0 τ t + 2 π S τ t t − π S τ t 2 = 2 π ( 2 f 0 v r c + 2 S R 0 c − 4 S R 0 v r c 2 ) t + 2 π ( 2 S v r c − 2 S v r 2 c 2 ) t 2 + ( 4 π R 0 f 0 c − 4 π S R 0 2 c 2 )

$$\begin{align} p_t(t)-p_r(t)&=2\pi f_0\tau_t+2\pi S\tau_t t-\pi S\tau_t^2 \notag\\ &=2\pi(\frac{2f_0v_r}{c}+\frac{2SR_0}{c}-\frac{4SR_0v_r}{c^2}) t+2\pi(\frac{2Sv_r}{c}-\frac{2Sv_r^2}{c^2}) t^2 + (\frac{4\pi R_0f_0}{c}-\frac{4\pi SR_0^2}{c^2}) \notag \end{align}$$ pt​(t)−pr​(t)​=2πf0​τt​+2πSτt​t−πSτt2​=2π(c2f0​vr​​+c2SR0​​−c24SR0​vr​​)t+2π(c2Svr​​−c22Svr2​​)t2+(c4πR0​f0​​−c24πSR02​​)​
因此可以知道，运动目标的中频信号依然是一个线性调频信号，调频斜率S’，差频fm’，初相phi’分别为：
$$S^{\prime }=\frac{2S{v}_r}{c}-\frac{2S{v}_r^2}{c^2}$$

$$f_m^{\prime }=\frac{2f_0{v}_r}{c}+\frac{2S{R}_0}{c}-\frac{4S{R}_0{v}_r}{c^2}$$

$${\varphi }^{\prime }=\frac{4\pi R_0{f}_0}{c}-\frac{4\pi S{R}_0^2}{c^2}$$

又由于：①光速的平方做分母，对应的项可约为0；②vr远小于c；③波长*频率=光速，因此可化简为：
$$S^{\prime }\approx \frac{2S{v}_r}{c}$$

$$f_m^{\prime }\approx \frac{2v_r}{\lambda }+\frac{2S{R}_0}{c}\approx f_m+f_d$$

$${\varphi }^{\prime }\approx \frac{4\pi R_0{f}_0}{c}=\frac{4\pi R_0}{\lambda }$$

2.2 测速原理

2.2.1 相位包含的信息

为表示振动方向引入了复数，用实部和虚部表示两个互相垂直的振动方向。以圆极化为例，红色曲线是电磁波在水平方向的投影，黄色曲线是电磁波在垂直方向的投影，黑色轴是电磁波的传播方向。当冲激信号1完整的转了一圈，电磁波在空间中走了多远呢？一个波长$\lambda$。即，电磁波在空间中转一圈$2\pi$，就传播了一个波长$\lambda$，反之也成立。发射信号的目标速度信息就体现在回波信号的相位变化上。雷达信号仿真的基本原理——时延与相位的变化


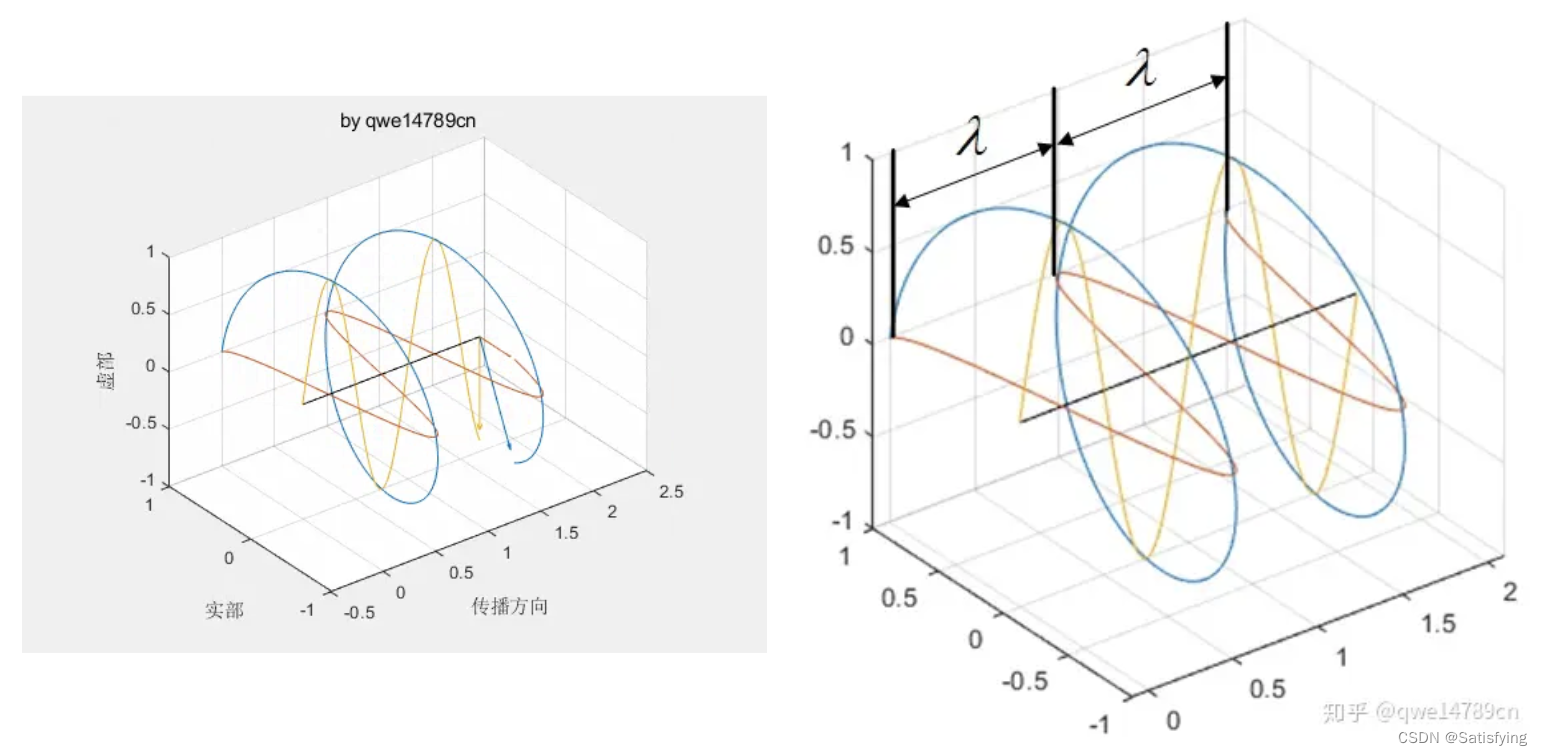
从上图可以看到，余下的长度是$\frac{2R}{\lambda }$的余数$r$，我们表示为
$r=2R-k\lambda$，其中k是整数，一个$\lambda$和一个$2\pi$对应，那么余下长度$r$对应的相位为：
$$\theta =\frac{r}{\lambda }\times 2\pi$$
因为相位变化也具有周期性，所以也可以表示为：
$$\theta =\frac{2R}{\lambda }\times 2\pi$$
将相位信息体现在指数上，那么发射信号的相位可以表示为：
$$e^{j\theta }=e^{j\frac{4\pi R}{\lambda }}$$
总之，回波信号由两部分决定：信号的时延（体现距离信息）、信号的相位变化（体现速度变化）。

2.2.2 原理推导

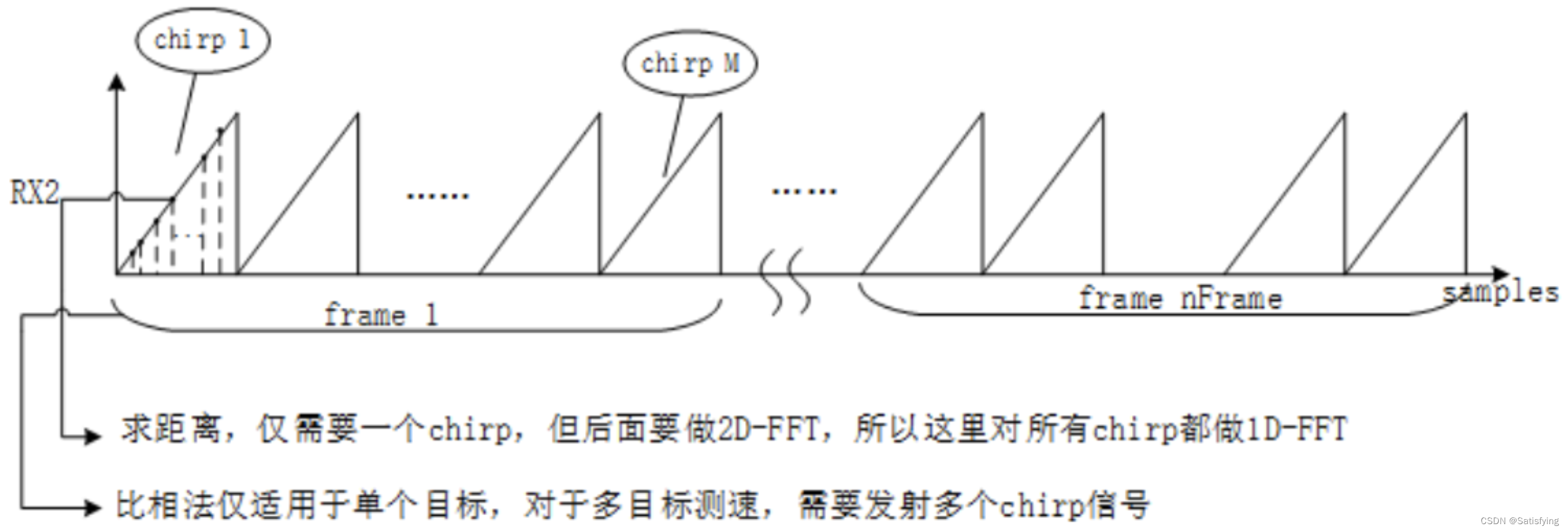
只有一个chrip就可以实现测距，因为频率信息内包含了距离信息（运动目标解算出来的是模糊距离）。因为一个chrip周期很短，近似将该时间段的目标看作是静止的，因此分析速度需要从多普勒维去看。也就是说，实现目标测速，必须发送多个chrip周期。

目标的速度信息是包含在不同chrip间回波信号的相位中的，连续发送L个chrip信号，其相位信息是随着chrip个数在不断变化的，因此对回波信号按照距离维-多普勒维排列存储之后，同一列的不同行对应的是相同频率、不同相位的回波信号（同频不同相）。具有相同频率、不同初始相位的正弦信号经过FFT变换，会在相同频率处产生峰值，但峰值信号的相位不同，峰值的相位等于正弦波的初始相位。因此对多普勒维做FFT，即可提取出回波信号的相位信息，即可解算出速度。中频信号对目标微小位移的灵敏度是非常高的。
$$\varphi =\frac{4\pi R_0}{\lambda }=\frac{4\pi v_r{T}_c}{\lambda }\Rightarrow v_r=\frac{\lambda \varphi }{4\pi T_c}$$

2.3 测角原理

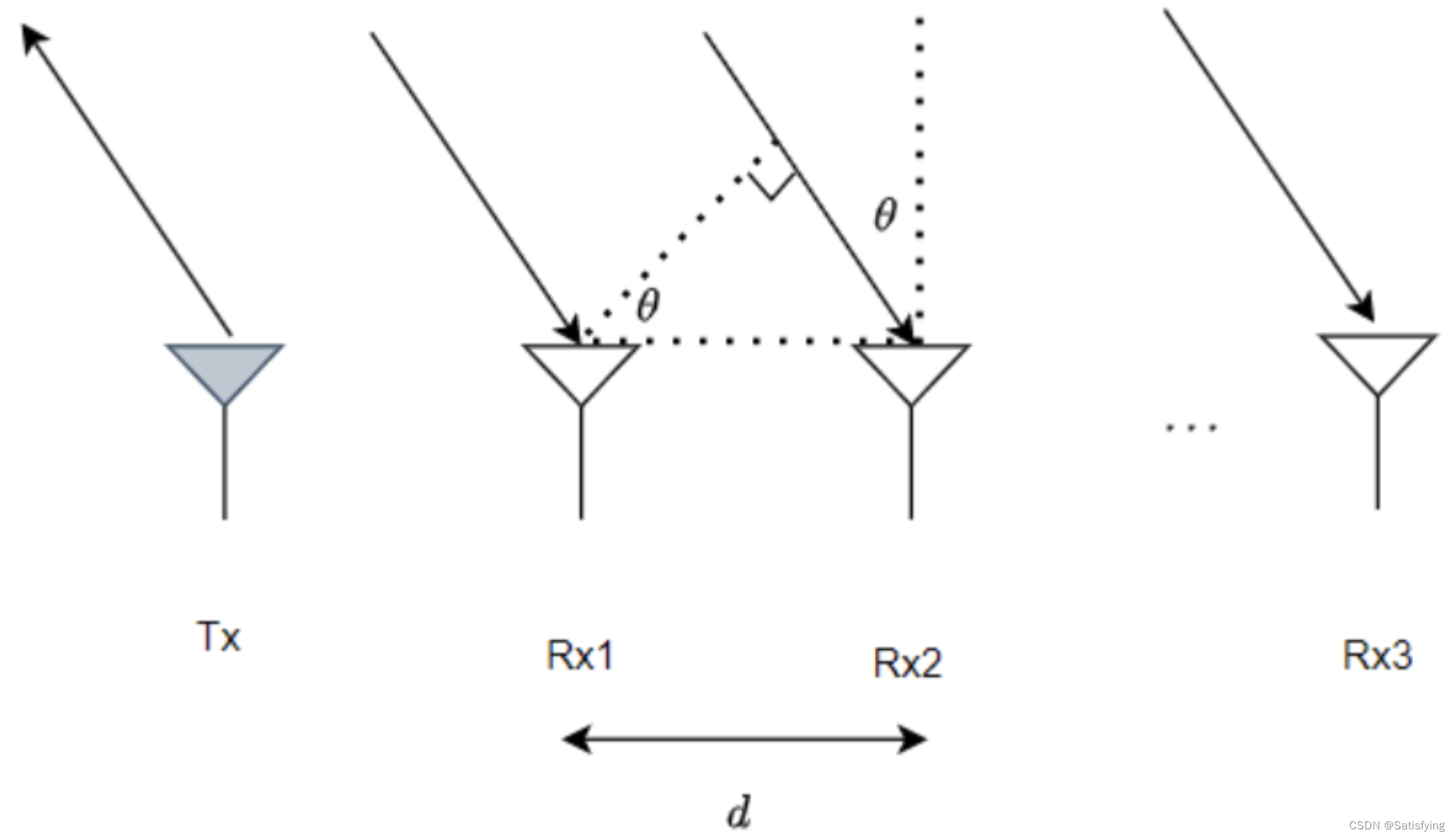
当目标距离发生微小变化时，Range-FFT峰值相位会发生较大的变化，因此可以利用物体与两个天线的距离差引起的相位变化估算到达角（Angle of Arrival, AOA）。实现测角原理，至少使用2个接收天线RX。

设相邻两个天线之间的排布间距为d，到达角为$\theta$，则相邻两个天线之间存在固定光程差$dsin\theta$，这个固定光程差会造成两个信道间的接收回波存在固定相位差，即：
$$\frac{dsin\theta }{\lambda }=\frac{\Delta \varphi }{2\pi }$$
因此，到达角可以求得：
$$\theta =arcsin(\frac{\lambda }{2\pi d}\Delta \varphi )$$

2.4 Matlab仿真

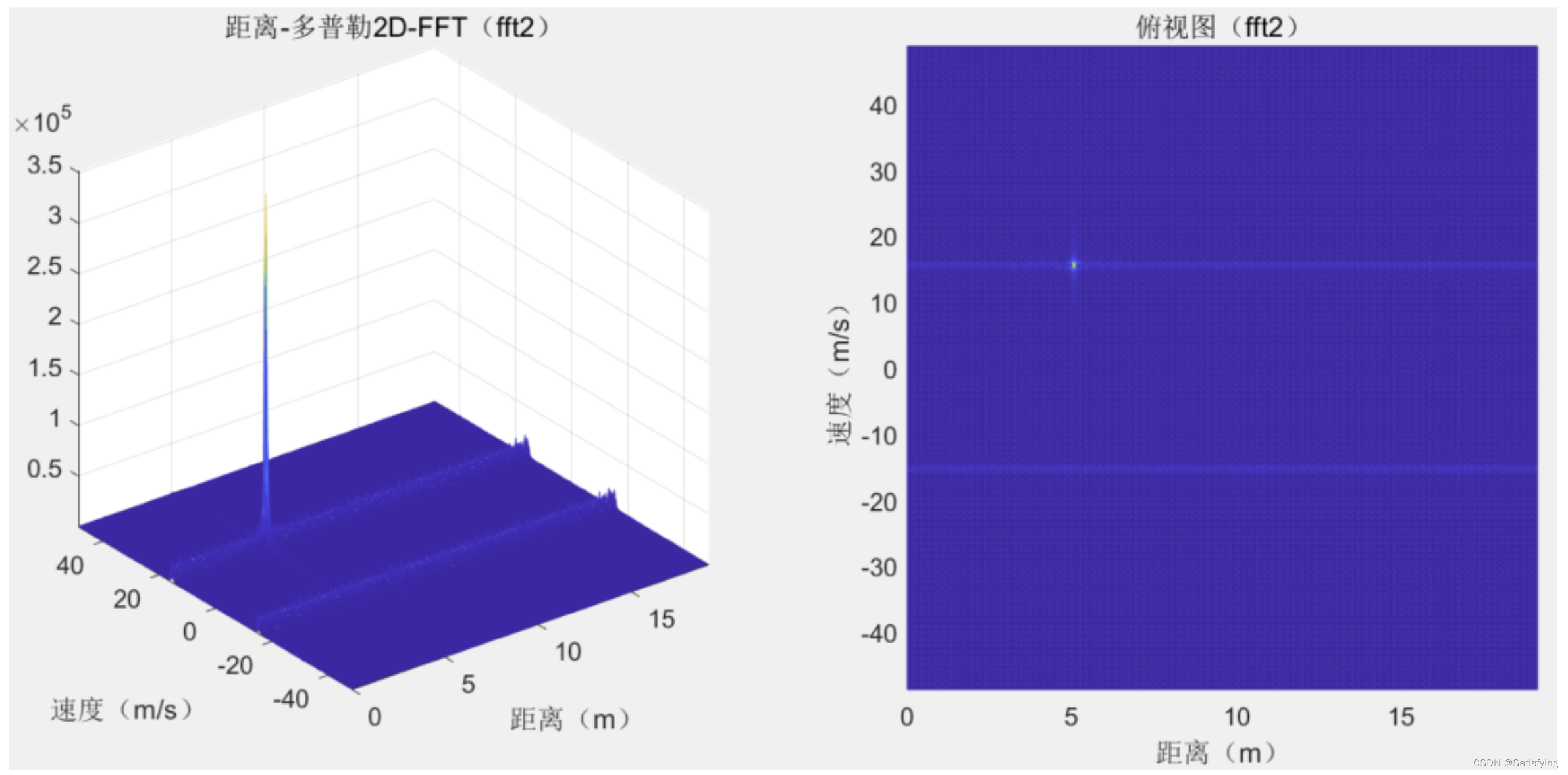
测速要进行RD分析。

clear; clc; close all; warning off;

%% 雷达参数设计
c = 3e8;  % 光速
fc = 77e9;  % 载频（77GHz）
lambda =  c / fc;  % 波长
B = 4e9;  % 扫频带宽（4GHz）
Tchrip = 20e-6;  % 扫频时宽（20us）
Nchrip = 256;  % 一个frame的chrip数量
fs = Nchrip / Tchrip;  % 采样率
Ns = 1024;  % 单个chrip周期内的采样点数
Tframe = Tchrip * Ns;  % 一个frame持续时长
S = B / Tchrip;  % 扫频斜率
Rx_num = 1;  % 接收天线数量

%% 测量参数计算
d_res = c / (2 * B);  % 距离分辨率
d_max = (c * fs) / (2 * S);  % 最大探测距离
v_max = lambda / (4 * Tchrip);  % 最大不模糊速度
v_res = lambda / (2 * Nchrip * Tchrip);  % 速度分辨率

%% 设置目标参数（单个目标）
d0 = 5;  % 目标位置
v0 = 15;  % 目标速度
rcs = 10;  % 目标RCS
sigma = 0.1;  % 高斯白噪声标准差

%% 产生混频信号
t = linspace(0, Tchrip, Ns);
ft = fc .* t + S .* t.^2 / 2;
St = cos(2 * pi .* ft);
Smix_frame = zeros(Nchrip, Ns);
for chrip = 1 : Nchrip
    d = d0 + v0 * (t + (chrip - 1) * Tchrip);
    tau = 2 .* d ./ c;  % 运动目标的时延是动态变化的
    Sr = zeros(1, Ns);
    for target = 1 : length(d0)
        fr = fc .* (t - tau(target, :)) + S * (t - tau(target, :)).^ 2 / 2;
        Sr = Sr + rcs(target) * cos(2 * pi * fr) + wgn(1, Ns, sigma(target));  % 总的回波信号=所有目标的回波信号之和
    end   
    Smix = St .* Sr;
    Smix_frame(chrip, :) = Smix;
end

%% 距离多普勒分析
Nfft_v = Nchrip * 2;
Nfft_d = Ns;
x = (0 : Nfft_d - 1) / Nfft_d * Ns * d_res;  % RDM横轴转换为距离
y = linspace(-v_max, v_max, Nfft_v);  % RDM横轴转换为速度
FFT_2D = abs(fftshift(fft2(Smix_frame, Nfft_v, Nfft_d), 1)); 

figure(1); clf;
subplot(1, 2, 1); mesh(x(1:Nfft_d/2), y, FFT_2D(:, 1:Nfft_d/2)); axis('tight'); set(gca, 'fontsize', 12);
xlabel('距离（m）'); ylabel('速度（m/s）'); title('距离-多普勒2D-FFT（fft2）');
subplot(1, 2, 2); mesh(x(1:Nfft_d/2), y, FFT_2D(:, 1:Nfft_d/2)); axis('tight'); set(gca, 'fontsize', 12); view(2);
xlabel('距离（m）'); ylabel('速度（m/s）'); title('俯视图（fft2）');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

三、总结

1. 测距仅需要一个chrip，如果是静止目标则计算的距离就是准确的，如果是运动目标那么就是有误差的模糊距离；测速需要多个chrip；测角需要多个天线；
2. 目标的距离信息包含在中频信息里，因此可以通过傅里叶变换求出fm’，再倒推出距离R0，但单个chrip只能完成测距功能；
3. FMCW雷达的差频信号依旧是个线性调频连续波，频率为收发信号频率差，相位为收发信号相位差；
4. 运动目标的差频 = 静止状态下的差频 + 多普勒频偏fd（fd为正还是为负取决于目标面向雷达还是远离雷达运动，目标远离雷达，回波信号频率低于发射信号频率，fd为负；反之fd为正）；
5. fm’不仅和目标距离R0有关，还和径向速度vr有关，而距离和径向速度有相关关系，通过fm’求得的距离R0存在误差，这就是距离速度耦合现象，最终得到的是模糊距离，当目标的运动速度越大时，耦合现象越严重，最终的测距误差也越大。因此需要进行速度补偿，也就是求出真实速度之后再对距离做修正。（三角波调制FMCW雷达可以无模糊地进行测距和测速，但会存在多目标配对的问题）
   

锯齿波调制的FMCW雷达差拍信号的推导及分析 - 晴天_en - 博客园

雷达原理 | 用MATLAB信号处理是如何解算目标的距离和速度信息的？

干货：FMCW雷达系统信号处理建模与仿真（含matlab代码）

TI 毫米波雷达基本原理(1)——测距原理_为什么fft变换能测距-CSDN博客

TI FMCW毫米波雷达基础(2)——测速原理_doppler range fft-CSDN博客

FMCW毫米波雷达基础原理学习一

Xiaojie雷达之路—毫米波雷达基础知识—中频信号的相位_雷达中频信号-CSDN博客

毫米波雷达：信号处理

FMCW毫米波雷达原理：测距、测速、测角

    

（本文完整的pdf请关注“张张学算法”，并回复“025”获取~）

    

本文由mdnice多平台发布