深度优先搜索基础篇（DFS算法）

一、基础概念

1、深度优先搜索

        深度优先搜索算法（Depth First Search，简称DFS）：一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(!n)。

       你可以把深度优先搜索想象成一个人在森林中探险。这个人从入口开始，选择一条路径一直走，直到走到这条路径的尽头。然后，他返回到上一个分叉点，选择另一条没有走过的路径继续探险，如此往复，直到他探索完所有可能的路径。

2、回溯

       想象你在森林里迷路了，你开始尝试各种方向，希望能找到出路。每当你觉得某个方向不对，或者走到了死胡同，你就会返回原来的地方，选择另一个方向继续前行。这就是回溯。在算法中，回溯意味着在搜索的过程中，每当遇到不符合条件的情况或者达到问题的边界时，就返回上一级状态，并尝试其他可能性，直到找到解或确定无解为止。

3、剪枝

        在森林里，有些方向你一看就知道是错的，比如朝着悬崖或者沼泽走。这时，你就不需要真的走过去再返回来，而是直接排除这些方向，选择其他更有希望的路。这就是剪枝。在算法中，剪枝是一种优化技术，通过提前判断某些选择不可能得到解，从而避免无效的搜索，减少计算量。

二、例题 

46. 全排列

此题是一道典型的深度优先搜索题，通过此题我们将了解dfs的基本思想以及解题模版步骤

画出决策树

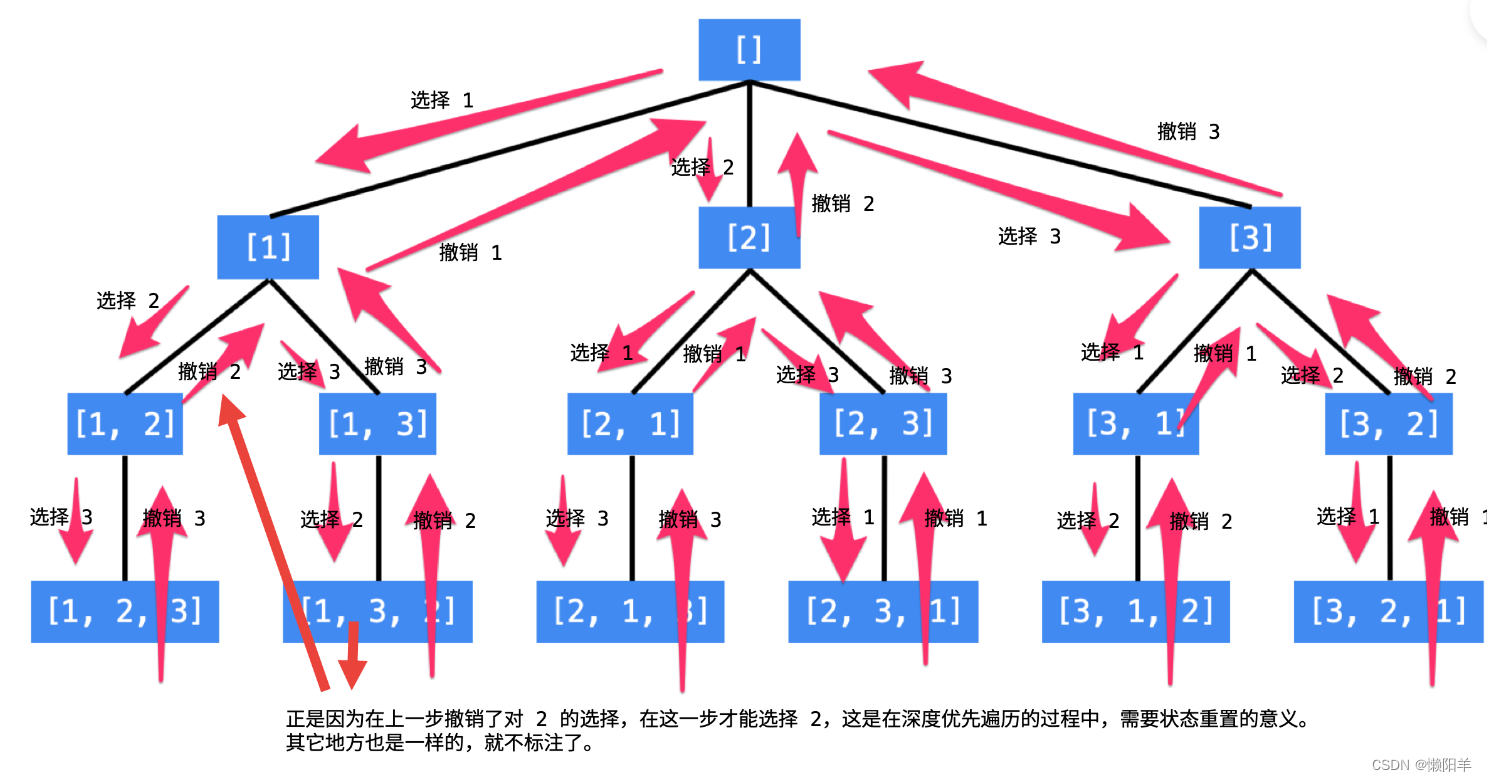
从以上决策树中不难看出，我们只需将这个树遍历完就可以得到所有全排列答案，决策树中的撤销操作就是回溯，而回溯完紧接着就需要剪枝

设计代码 

1、创建全局变量：

int** ret;   // 记录所有排列结果的二维数组  
int* path;   // 记录一种排列结果的一维数组  
bool* check; // 标记数组元素是否被使用的一维数组  

 设计主函数：

int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes) {  
// nums:需要排列的一维数组，numsSize:nums元素个数，returnSize:返回的二维数组的行数,returnColumnSizes:记录二维数组每行的列数的一维数组.*returnColumnSizes表示此数组的数组名
 
    //初始化变量
    *returnSize = 0;  
    *returnColumnSizes = (int*)malloc(sizeof(int) * INT_MAX);  
    ret = (int**)malloc(sizeof(int*) * INT_MAX);  
    path = (int*)malloc(sizeof(int) * numsSize);  
    check = (bool*)malloc(sizeof(bool) * numsSize);  
    for (int i = 0; i < numsSize; i++) {  
        check[i] = true;  
    }  
    // 开始深度优先搜索  
    dfs(nums, numsSize, returnSize, returnColumnSizes, 0); // 从深度 0 开始  
    // 释放中间使用的全局变量  
    free(path);  
    free(check);  
    return ret;  
}  

 2、设计dfs函数

dfs本质上是一个递归函数，我们还是用三步法设计：

• 确定函数返回类型和参数：由于我们直接修改全局变量的方式来返回答案，所以dfs函数返回值为void，函数参数在主函数的四个参数上新增一个depth，记录path数组（当前这种排列）下标
• 确定递归出口：将每种排列结果都记录在path这个数组中，所以当path下标增至与numsSize相等时，代表所有数都已被排列，则结束递归。
• 确定函数体：首先遍历check数组，如果哪个数未被使用(true)，则将其排列使用放到path中，随后在check将此数标记为已使用(false)，然后递归将其他数继续放到path中

void dfs(int* nums, int numsSize, int* returnSize, int** returnColumnSizes, int depth) {  
    if (depth == numsSize) {  
        int* temp = (int*)malloc(sizeof(int) * numsSize);  
        for (int i = 0; i < numsSize; i++) {  
            temp[i] = path[i];  
        }  
        ret[*returnSize] = temp;  
        (*returnColumnSizes)[*returnSize] = numsSize;  
        (*returnSize)++;  
        return;  
    }  
 
    for (int i = 0; i < numsSize; i++) {  
        if (check[i]) {  
            path[depth] = nums[i]; // 将当前数字放入 path 的正确位置  
            check[i] = false;  
            dfs(nums, numsSize, returnSize, returnColumnSizes, depth + 1); // 递归调用，深度增加  
            check[i] = true; // 回溯，重置 check[i]  
        }  
    }  
}  

回溯与剪枝

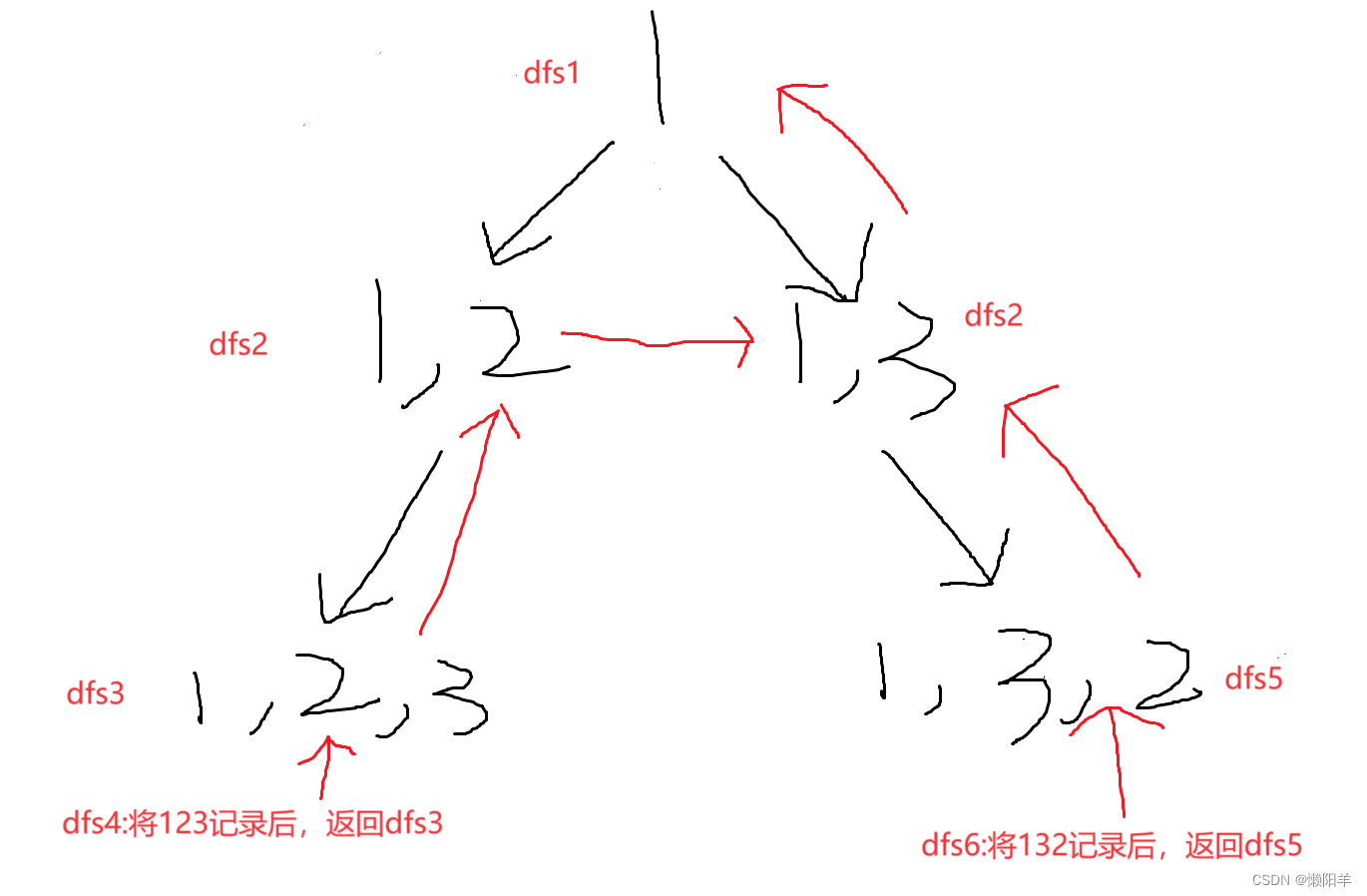
 先来看看dfs刚开始是怎么运行的：

在第一次dfs中将path第一个数赋为1

随后开始dfs2，1已被标记使用过，然后只能按顺序将2加入path数组

随后开始dfs3，1,、2已被标记，只能将3加入

最后dfs4进入递归边界直接返回到dfs3，开始回溯

在dfs3的for循环中，将3清除标记， i 已遍历完整个nums数组，直接结束for循环并返回到dfs2

dfs2中先将2清除标记，随后for循环继续进行，由于3已被清除标记，所以将3放入path中2的位置

随后进行dfs5将2放入path数组，以此类推，直到dfs6结束后，因为dfs2中 i 已遍历完整个nums数组，dfs2中for循环结束。所以dfs6结束后一口气直接回溯到的dfs1

随后dfs1中的for循环继续，将2放入path中1的位置以此类推，直至遍历完所有排列

关键点：

1、在dfs的for循环中，用 i 来遍历原本数组，用 depth 来记录当前排列数组下标，二者是分开不干扰的。所以for循环的本意为：遍历nums数组，将所有未使用的数依次赋给path中下标depth的位置，由此得到所有排列。所以不考虑递归，在同一次dfs中depth的值不变，每次进入for循环，只改变path中下标为depth的数，随后调用递归，改变下标depth+1的数。

2、剪枝中巧妙的一点：我们在dfs形参中直接传递的是depth+1常数值而不是指针，所以在递归中不改变depth的值，因此回溯时无需depth-1（depth的值与调用递归前一样，递归未改变depth的值）。

3、此题中对于剪枝的理解：每次在for循环中调用一次dfs时，由于不断递归深入，最终会得到将nums[i]放到path[depth]位置的所有排列结果，所以每次调用dfs后（depth位置是nums[i]这个数的所有排列都已得出），只需考虑将depth位置未放置过的数继续放到depth位置并求出其所有排列。所以将已排列过的nums[i]标记为false，随后继续for循环，继续将其他数放到depth位置求出其所有排列。

 总代码

int** ret;   // 记录所有排列结果的二维数组  
int* path;   // 记录一种排列结果的一维数组  
bool* check; // 标记数组元素是否被使用的一维数组  
  
void dfs(int* nums, int numsSize, int* returnSize, int** returnColumnSizes, int depth) {  
    if (depth == numsSize) {  
        int* temp = (int*)malloc(sizeof(int) * numsSize);  
        for (int i = 0; i < numsSize; i++) {  
            temp[i] = path[i];  
        }  
        ret[*returnSize] = temp;  
        (*returnColumnSizes)[*returnSize] = numsSize;  
        (*returnSize)++;  
        return;  
    }  
 
    for (int i = 0; i < numsSize; i++) {  
        if (check[i]) {  
            path[depth] = nums[i]; // 将当前数字放入 path 的正确位置  
            check[i] = false;  
            dfs(nums, numsSize, returnSize, returnColumnSizes, depth + 1); // 递归调用，深度增加  
            check[i] = true; // 回溯，重置 check[i]  
        }  
    }  
}  
  
int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes) {  
// nums:需要排列的一维数组，numsSize:nums元素个数，returnSize:返回的二维数组的行数,returnColumnSizes:记录二维数组每行的列数的一维数组.*returnColumnSizes表示此数组的数组名
 
    *returnSize = 0;  
    *returnColumnSizes = (int*)malloc(sizeof(int) * 1000);  
    ret = (int**)malloc(sizeof(int*) * 1000);  
    path = (int*)malloc(sizeof(int) * numsSize);  
    check = (bool*)malloc(sizeof(bool) * numsSize);  
    for (int i = 0; i < numsSize; i++) {  
        check[i] = true;  
    }  
    // 开始深度优先搜索  
    dfs(nums, numsSize, returnSize, returnColumnSizes, 0); // 从深度 0 开始  
    // 释放中间使用的全局变量  
    free(path);  
    free(check);  
    return ret;  
}