devbox
天景科技苑
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

算法——动态规划（DP）_dp动态规划

作者：天景科技苑 | 2024-07-23 15:44:34

赞

踩

dp动态规划

目录

DP

0/1背包问题和完全背包问题

1、完全背包问题

2、1100: 采药

3、1103: 开心的金明

4、1175: 金明的预算方案

 求解斐波那契数列

 爬楼梯

拿金币

印章

过河马

进击的青蛙

砝码称重

B君的希望

1108: 守望者的逃离

1174: 计算直线的交点数

1191: 化学品问题

1193: 半数集问题

1217: 换位置

5、最长回文串

动态规划通常用于求解最优化问题，如最长路径、最大值、最小值等。递归则更常用于遍历、搜索和排列组合等问题

DP

  • 动态规划通常以自底向上或自顶向下的方式进行求解。

    • 自底向上的动态规划从最简单的子问题开始，逐步解决更复杂的问题，直到达到原始问题。

    • 自顶向下的动态规划则从原始问题出发，分解成子问题，并逐步求解这些子问题。

  • 动态规划算法通常通过填表或递推的方式来求解最优解，以减少重复计算，提高计算效率。

  • 求解DP问题的步骤：
    • 1、定义状态
    • 2、状态转移 
      • 确定状态转移方程
    • 3、定义初始状态
  • DP可以解决的问题需满足三个条件：
    • 1、问题有最优解
    • 2、有大量子问题重复（DP可以把求解的结果存起来，后续用到时直接查询）
    • 3、当前阶段的求解只与前面的阶段有关，与之后的阶段无关

0/1背包问题和完全背包问题

  1. 0/1背包问题：

    • 每种物品最多只能选择一次放入背包中。
    • 物品的数量有限，即每种物品只有一个。
    • 物品放入背包后不可再取出。

  2. 完全背包问题：

    • 每种物品可以选择多次放入背包中。
    • 物品的数量无限，可以重复选择。
    • 物品放入背包后可以再取出。

针对这两种不同的情况，动态规划的状态转移方程稍有不同。

对于0/1背包问题，状态转移方程如下：

  • 当第 i 个物品放不进背包时，即 j<w[i] 时，有 dp[i][j]=dp[i-1][j]；
  • 当第 i 个物品可以放进背包时，即 j>=w[i] 时，有 dp[i][j]=max(dp[i-1][j], dp[i-1][j-w[i]]+v[i])。

对于完全背包问题，状态转移方程如下：

  • 当第 i 个物品放不进背包时，即 j<w[i] 时，有 dp[i][j]=dp[i-1][j]；
  • 当第 i 个物品可以放进背包时，即 j>=w[i] 时，有 dp[i][j]=max(dp[i-1][j], dp[i][j-w[i]]+v[i])。这里与0/1背包问题不同的是，这里是 dp[i][j-w[i]] 而不是 dp[i-1][j-w[i]]，表示可以重复选择第 i 个物品。 

1、完全背包问题

问题描述

　　有一個背包，容量為M。有N種物品，每種物品有其体积Wi与价值Vi。將這些物品的一部分放入背包，每種物品可以放任意多個，要求总体积不超過容量，且总价值最大。

输入格式

　　第一行為N, M。
　　之後N行，每行為Wi, Vi。

输出格式

　　一個數，為最大價值。

样例输入

3 20
15 16
6 6
7 5

样例输出

18

数据规模和约定

　　N, M<=1000。

分析：

  •  dp[j]表示背包容量为 j 时的最大总价值
  1. package no1_1;
  2. import java.util.Scanner;
  3.  
  4. public class Main {
  5.     public static void main(String[] args) {
  6.         Scanner scanner = new Scanner(System.in);
  7.         int n = scanner.nextInt(); // 读入物品数量
  8.         int m = scanner.nextInt(); // 读入背包容量
  9.  
  10.         int[] volumes = new int[n]; // 物品体积数组
  11.         int[] values = new int[n]; // 物品价值数组
  12.  
  13.         // 读入物品信息
  14.         for (int i = 0; i < n; i++) {
  15.             volumes[i] = scanner.nextInt();
  16.             values[i] = scanner.nextInt();
  17.         }
  18.  
  19.         int[] dp = new int[m + 1];
  20.  
  21.         // 动态规划求解
  22.         for (int i = 0; i < n; i++) { // 遍历每种物品
  23.             for (int j = volumes[i]; j <= m; j++) { // 遍历每种背包容量
  24.                 dp[j] = Math.max(dp[j], dp[j - volumes[i]] + values[i]); // 状态转移方程
  25.             }
  26.         }
  27.  
  28.         // 输出背包能装下的最大价值
  29.         System.out.println(dp[m]);
  30.     }
  31. }

2、1100: 采药

题目描述
辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。” 


如果你是辰辰，你能完成这个任务吗？

输入格式
输入第一行有两个整数T（1 <= T <= 1000）和M（1 <= M <= 100），用一个空格隔开，T代表总共能够用来采药的时间，M代表山洞里的草药的数目。接下来的M行每行包括两个在1到100之间（包括1和100）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式
输出一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

样例输入
70 3
71 100
69 1
1 2
样例输出
3

属于0/1背包问题类型

  1. package no1_1;
  2. import java.util.*;
  3.  
  4. public class Main {
  5.     public static void main(String[] args) {
  6.         Scanner scanner = new Scanner(System.in);
  7.         int t=scanner.nextInt();
  8.         int m=scanner.nextInt();
  9.         int[][] herbMedicine=new int[m][2];
  10.         for(int i=0;i<m;i++) {
  11.         	scanner.nextLine();
  12.         	herbMedicine[i][0]=scanner.nextInt();
  13.         	herbMedicine[i][1]=scanner.nextInt();
  14.         }
  15.         int[] dp=new int[t+1];//dp[j]表示时间为j时能采到的草药的最大价值
  16.         for(int i=0;i<m;i++) {//遍历每一种草药
  17.         	for (int j = t; j >= herbMedicine[i][0]; j--) {
  18.                 dp[j] = Math.max(dp[j], dp[j - herbMedicine[i][0]] + herbMedicine[i][1]);
  19.             }
  20.         }
  21.         System.out.println(dp[t]);
  22.     }
  23. }

3、1103: 开心的金明

题目描述
金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间他自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过N元钱就行”。今天一早金明就开始做预算，但是他想买的东西太多了，肯定会超过妈妈限定的N元。于是，他把每件物品规定了一个重要度，分为5等：用整数1~5表示，第5等最重要。他还从因特网上查到了每件物品的价格（都是整数元）。他希望在不超过N元（可以等于N元）的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第j件物品的价格为v[j]，重要度为w[j]，共选中了k件物品，编号依次为j1，j2，……，jk，则所求的总和为：

v[j1]*w[j1]+v[j2]*w[j2]+ …+v[jk]*w[jk]。（其中*为乘号）

请你帮助金明设计一个满足要求的购物单。

输入格式
输入第1行，为两个正整数，用一个空格隔开：N m

（其中N（<30000）表示总钱数，m（<25）为希望购买物品的个数。）

从第2行到第m+1行，第j行给出了编号为j-1的物品的基本数据，每行有2个非负整数v p

（其中v表示该物品的价格(v<=10000)，p表示该物品的重要度(1~5)）

输出格式
输出只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值（<100000000）。

样例输入
1000 5
800 2
400 5
300 5
400 3
200 2
样例输出
3900

  1. package no1_1;
  2. import java.util.*;
  3. public class Main {
  4.     public static void main(String[] args) {
  5.         Scanner scanner = new Scanner(System.in);
  6.         int n=scanner.nextInt();
  7.         int m=scanner.nextInt();
  8.         int[][] things=new int[m][2];
  9.         for(int i=0;i<m;i++) {
  10.         	scanner.nextLine();
  11.         	things[i][0]=scanner.nextInt();
  12.         	things[i][1]=scanner.nextInt();
  13.         }
  14.         int[] dp=new int[n+1];//dp[j]表示使用j元购买到的物品与其重要度的乘积和
  15.         for(int i=0;i<m;i++) {//枚举这m件物品
  16.         	for(int j=n;j>=0;j--) {
  17.         		if(j>=things[i][0]) {//j元可以购买该物，再考虑要不要买
  18.             		dp[j]=Math.max(dp[j], dp[j-things[i][0]]+things[i][0]*things[i][1]);
  19.         		}
  20.         	}
  21.         }
  22.         System.out.println(dp[n]);
  23.     }
  24. }

4、1175: 金明的预算方案

题目描述
金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用 的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过N元钱就行”。今天一早，金明就开始做预 算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：

主件 附件
电脑 打印机，扫描仪
书柜 图书
书桌 台灯，文具
工作椅 无

如果要买归类为附件的物品，必须先买该附件所属的主件。每个主件可以有0个、1个或2个附件。附件不再有从属于自己的附件。金明想买的东西很 多，肯定会超过妈妈限定的N元。于是，他把每件物品规定了一个重要度，分为5等：用整数1~5表示，第5等最重要。他还从因特网上查到了每件物品的价格 （都是10元的整数倍）。他希望在不超过N元（可以等于N元）的前提下，使每件物品的价格与重要度的乘积的总和最大。
设第j件物品的价格为v[j]，重要度为w[j]，共选中了k件物品，编号依次为j1，j2，……，jk，则所求的总和为：
v[j1]*w[j1]+v[j2]*w[j2]+ …+v[jk]*w[jk]。（其中*为乘号）
请你帮助金明设计一个满足要求的购物单。

输入格式
第1行，为两个正整数，用一个空格隔开：
N m
（其中N（<32000）表示总钱数，m（<60）为希望购买物品的个数。）
从第2行到第m+1行，第j行给出了编号为j-1的物品的基本数据，每行有3个非负整数
v p q
（其中v表示该物品的价格（v<10000），p表示该物品的重要度（1~5），q表示该物品是主件还是附件。如果q=0，表示该物品为主件，如果q>0，表示该物品为附件，q是所属主件的编号）

输出格式
只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值（<200000）。

样例输入
1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0
样例输出
2200

与上一道题类似

区别在于，在计算要不要买当前这件物品时，还要算上它的主件的价格（如果有的话）

  1. import java.util.*;
  2.  
  3. public class Main {
  4.     public static void main(String[] args) {
  5.     	Scanner scanner=new Scanner(System.in);
  6.     	int n=scanner.nextInt();
  7.     	int m=scanner.nextInt();
  8.     	int[][] things=new int[m][3];
  9.     	for(int i=0;i<m;i++) {//i+1为该物品的编号
  10.     		scanner.nextLine();
  11.     		things[i][0]=scanner.nextInt();//物品的价格
  12.     		things[i][1]=scanner.nextInt();//物品的重要度
  13.     		things[i][2]=scanner.nextInt();//物品是主件还是附件
  14.     	}
  15.     	
  16.     	int[] dp=new int[n+1];
  17.     	for(int i=0;i<m;i++) {//枚举m个物品
  18.     		for(int j=n;j>=0;j--) {
  19.     			int sumValue=things[i][0];
  20.     			int sumImportance=things[i][0]*things[i][1];
  21.     			if(things[i][2]>0) {
  22.     				int number=things[i][2]-1;//该附件对应的主件的编号
  23.     				sumValue+=things[number][0];//加上该附件对应的主件的价格
  24.     				sumImportance+=things[number][0]*things[number][1];
  25.     			}
  26.     			if(j>=sumValue) {//j元可以购买该物（及其主件），再考虑要不要买
  27.     				dp[j]=Math.max(dp[j], dp[j-sumValue]+sumImportance);
  28.     			}
  29.     		}
  30.     	}
  31.     	System.out.println(dp[n]);
  32.     }
  33. }

 求解斐波那契数列

  1. public class Fibonacci {
  2.     // 计算斐波那契数列的值，使用动态规划方法
  3.     public int calculateFibonacci(int n) {
  4.         if (n <= 1) {
  5.             return n;  // 当n为0或1时，直接返回n，无需计算
  6.         }
  7.         // 创建一个数组来保存中间结果，避免重复计算
  8.         int[] dp = new int[n + 1];
  9.         dp[0] = 0; // 初始化数组第一个元素为0
  10.         dp[1] = 1; // 初始化数组第二个元素为1
  11.         // 从第三个位置开始计算斐波那契数列的值
  12.         for (int i = 2; i <= n; i++) {
  13.             dp[i] = dp[i - 1] + dp[i - 2];  // 根据动态规划定义计算第i个斐波那契数列的值
  14.         }
  15.         return dp[n];  // 返回第n个斐波那契数列的值
  16.     }
  17.  
  18.     public static void main(String[] args) {
  19.         Fibonacci fib = new Fibonacci();
  20.         int n = 10;
  21.         int result = fib.calculateFibonacci(n);
  22.         System.out.println("第 " + n + " 个斐波那契数列的值为：" + result);
  23.     }
  24. }

 爬楼梯

假设有n(1\leq n\leq 50)级楼梯，每次只能爬1级或2级，有多少种方法可以爬到楼梯的顶部？

分析：

  • 在爬上第 i 级楼梯之前 ，爬楼梯的人一定站在第 i-1 级楼梯或第 i-2 级楼梯上，两种情况
  • 所以爬上第 i 级楼梯的方法等于两种走法之和（站在第i-1级楼梯，站在第i-2级楼梯上）
  • 此处涉及到应用组合数学的加法规则：（“或”）
    • 如果一个事件以 a 种方式发生，第二个事件以 b 种（不同）方式发生，那么存在 a+b 种方式
  • dp[i]表示爬上第i级楼梯有多少种走法
    • dp[1]=1
    • dp[2]=2
    • dp[i]=dp[i-1]+dp[i-2]，i>2（状态转移方程）

1、辅助数组

时间复杂度O(n)，空间复杂度O(n)

  1. package no1_1;
  2. import java.util.Scanner;
  3. public class example {
  4. 	public static void main(String[] args) {
  5. 		Scanner sc=new Scanner(System.in);
  6. 		int n=sc.nextInt();
  7. 		int[] dp=new int[n+1];
  8. 		dp[1]=1;
  9. 		dp[2]=2;
  10. 		for(int i=3;i<=n;i++) {
  11. 			dp[i]=dp[i-2]+dp[i-1];
  12. 		}
  13. 		System.out.println(dp[n]);
  14. 	}
  15. }

2、只使用两个变量记录前两项的值

时间复杂度O(n)，空间复杂度O(1)

  1. package no1_1;
  2. import java.util.Scanner;
  3. public class example {
  4. 	public static void main(String[] args) {
  5. 		Scanner sc=new Scanner(System.in);
  6. 		int n=sc.nextInt();
  7. 		int val1=1,val2=2,result=0;;
  8. 		for(int i=3;i<=n;i++) {//val1：前一项；val2：当前项
  9. 			result=val1+val2;
  10. 			val1=val2;
  11. 			val2=result;
  12. 		}
  13. 		System.out.println(result);
  14. 	}
  15. }

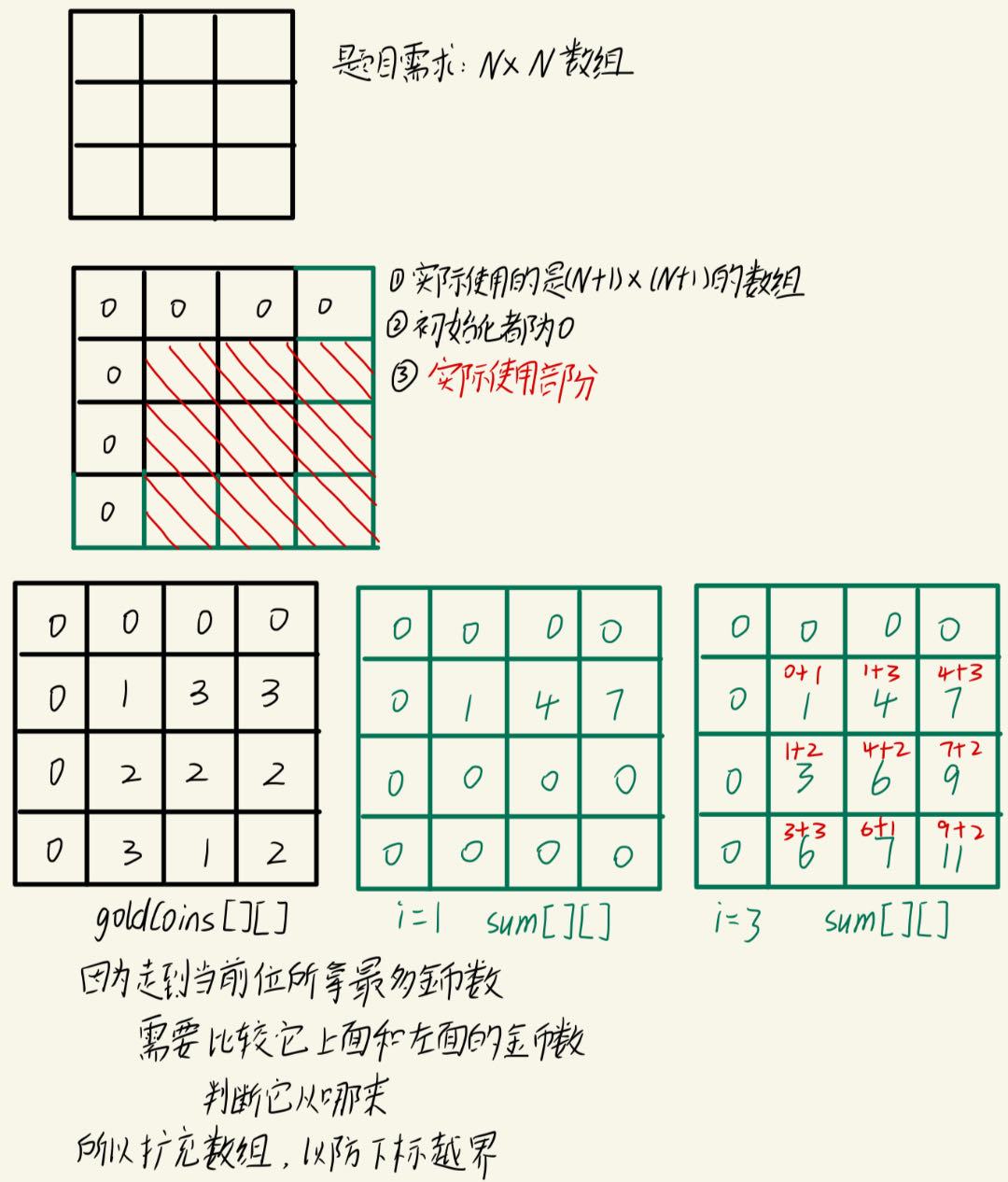
拿金币

有一个N x N的方格,每一个格子都有一些金币,只要站在格子里就能拿到里面的金币。你站在最左上角的格子里,每次可以从一个格子走到它右边或下边的格子里。请问如何走才能拿到最多的金币。

分析：

  • 当前位的最大金币数，需要上一位也拿到最大金币数

  1. package no1_1;
  2. import java.util.Scanner;
  3. public class Main {
  4. 	public static void main(String[] args) {
  5. 		Scanner scanner = new Scanner(System.in);
  6. 		int n = scanner.nextInt();
  7. 		//根据输入，把金币放入数组中对应的位置
  8. 		int[][] goldCoins = new int[n + 1][n + 1];
  9. 		for (int i = 1; i <= n; i++) {
  10. 			for (int j = 1; j <= n; j++) {
  11. 				goldCoins[i][j] = scanner.nextInt();
  12. 			}
  13. 		}
  14. 		//该数组存储的是走到当前位置所拿的最多金币数
  15. 		int[][] sum = new int[n + 1][n + 1];
  16. 		for (int i = 1; i <= n; i++) {
  17. 			for (int j = 1; j <= n; j++) {
  18. 				//当前位的最大金币数，需要上一位也拿到最大金币数，
  19. 				//该循环看的是sum[i][j]，一直是往前走的，不要被i-1和j-1误了眼，觉得是倒退着走，i-1和j-1只是判断上一步是应该在哪里
  20. 				if (sum[i][j - 1] > sum[i - 1][j]) {
  21. 					sum[i][j] = sum[i][j - 1] + goldCoins[i][j];
  22. 				} else {
  23. 					sum[i][j] = sum[i - 1][j] + goldCoins[i][j];
  24. 				}
  25. 			}
  26. 		}
  27. 		
  28. 		System.out.println(sum[n][n]);
  29. 	}
  30. }

印章

共有n种图案的印章，每种图案的出现概率相同。小A买了m张印章，求小A集齐n种印章的概率。

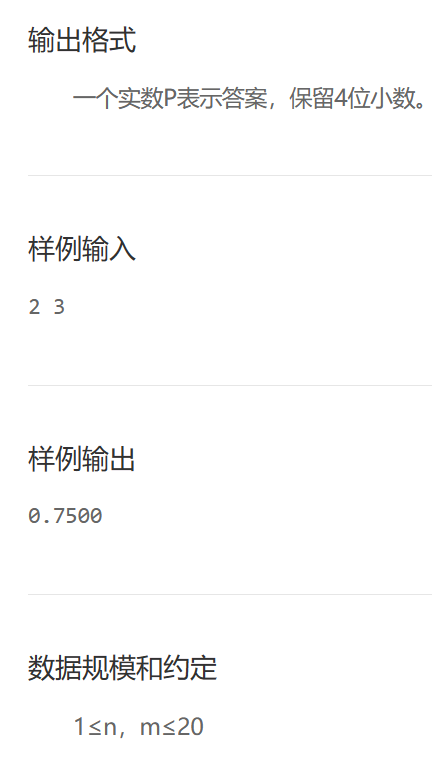
分析：

  • i：买的印章数
  • j：凑齐的印章数
  • dp[i][j]：买了 i 个印章，凑齐了 j 种的概率
  • 概率 p=1 / n 
  • 情况一：
    • i < j
    • 不可能凑齐，dp[i][j]=0
  • 情况二：
    • j == 1
    • 买了 i 张印章，凑齐的印章为图案1时，概率为p^{i}
    • 但有 n 种印章图案，总的概率等于每个种图案的概率和（应用组合数学的加法规则 ）
    • 即p^{i}\times n，而 p = 1 / n，所以
    • dp\left [ i \right ]\left [ 1 \right ]=(\frac{1}{n})^{i-1}
  • 情况三：

    • i >= j

    • 为下面两种情况相加（应用组合数学的加法规则）

    • 1、买了 i - 1 张 已经得到了 j 种，最后一张随便

      • dp[i] [j] = dp[i-1] [j] * ( j / n )

        • dp[i-1] [j]是买了 i - 1 张 已经得到了 j 种的概率

        • j / n是最后一张随便哪种的概率

    • 2、买了 i - 1 张 只得到了 j - 1 种，最后一张是第 j 种

      • dp[i] [j] = dp[i-1] [j-1] * （n-（j-1）） / n

        • dp[i-1] [j-1]是买了 i - 1 张 只得到了 j - 1 种的概率

        • （n-（j-1）） / n是买最后一张是第 j 种的概率

  1. package no1_1;
  2. import java.util.*;
  3. public class Main {
  4.     public static void main(String[] args) {    	
  5.         Scanner sc=new Scanner(System.in); 
  6.         int n=sc.nextInt();
  7.         int m=sc.nextInt();
  8.         double[][] array=new double[m+1][n+1];
  9.         System.out.printf("%.4f",probability(array,n,m));//动态规划
  10.     }
  11.     public static double probability(double[][] array,int n,int m) {
  12.     	double p=1.0/n;
  13.     	for(int i=1;i<=m;i++) {//买的印章数
  14.     		for(int j=1;j<=n;j++) {//凑齐的印章数
  15.     			if(i<j) {//买的印章数少于种类数，不可能凑齐
  16.     				array[i][j]=0;
  17.     			}else if(j==1) {//只凑齐了一种
  18.     				array[i][j]=Math.pow(p, i-1);
  19.     			}else {
  20.     				//为下面两种情况相加，（应用组合数学的加法规则）
  21.     				//1、买了 i - 1 张 已经得到了 j 种，最后一张随便， dp[i] [j] = dp[i-1] [j] * ( j / n )
  22.     				//2、买了 i - 1 张 只得到了 j - 1 种，最后一张是第 j 种， dp[i] [j] = dp[i-1] [j-1] * (n-j+1) / n
  23.     				array[i][j]=array[i-1][j]*(j*p)+array[i-1][j-1]*((n-j+1)*p);
  24.     			}
  25.     		}
  26.     	}
  27.     	return array[m][n];
  28.     }
  29. }

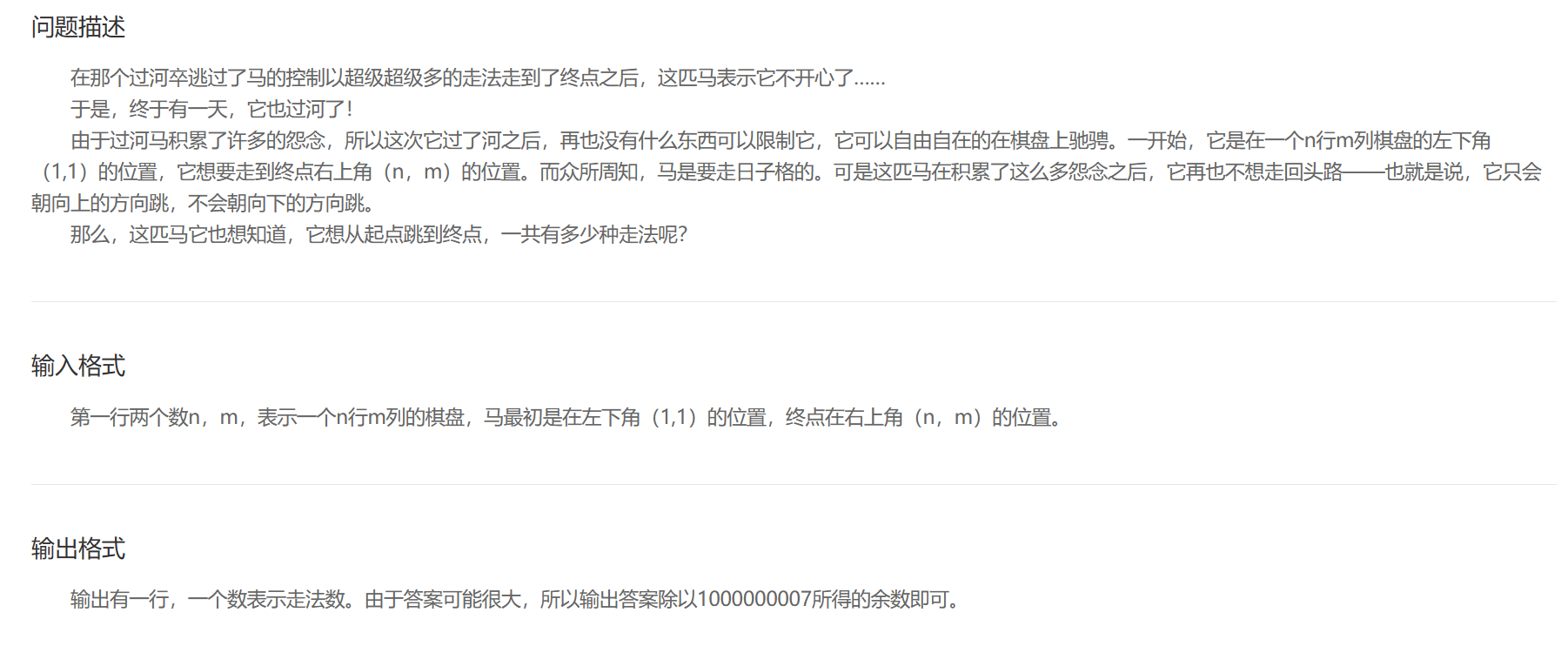
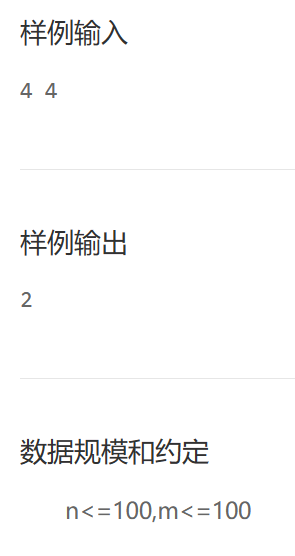
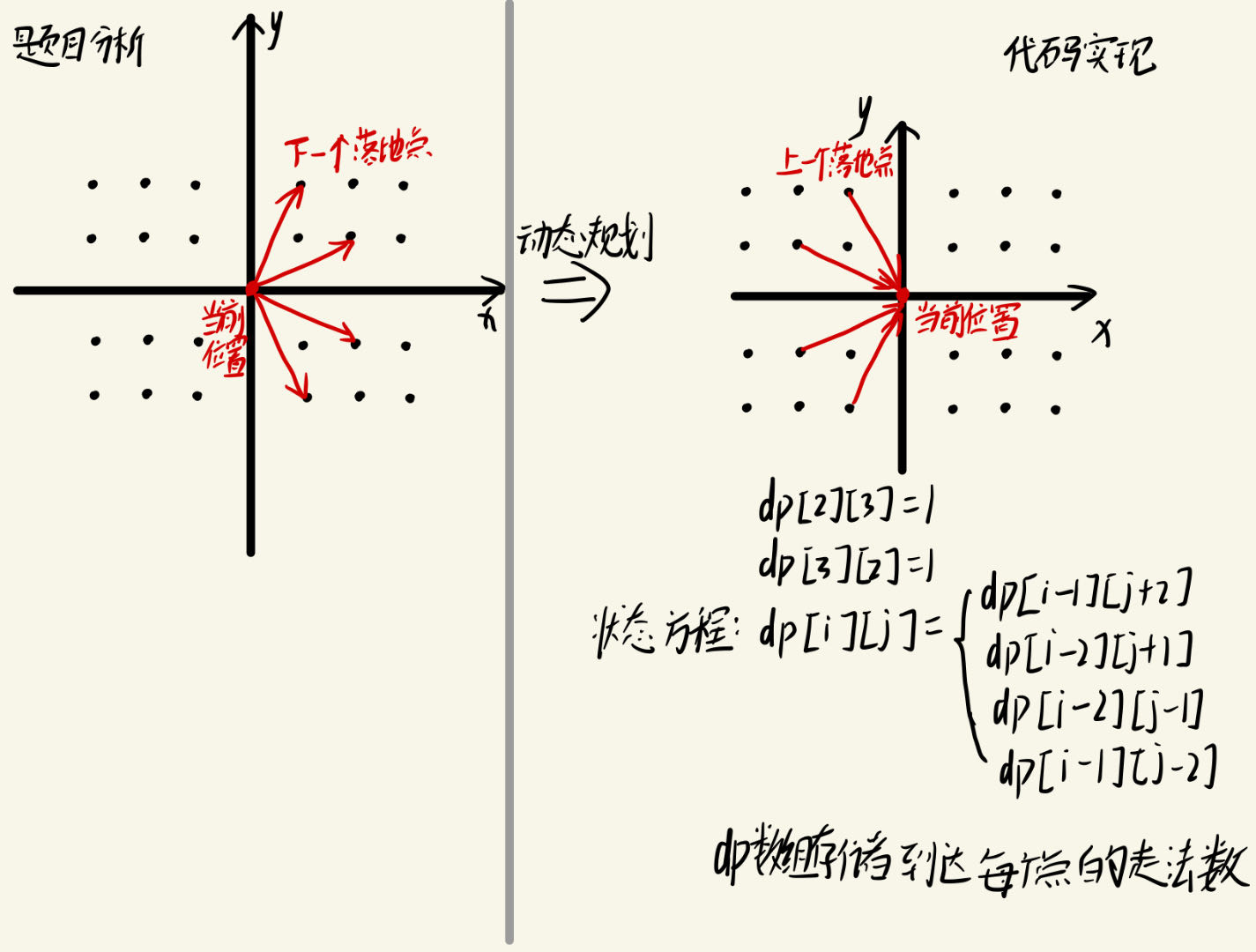
过河马

分析：

  •  马不会走回头路的意思是：跳的下一个点的行坐标必须大于现在的行坐标
  1. import java.util.*;
  2. public class Main {
  3.     public static void main(String[] args) {
  4.         Scanner input=new Scanner(System.in);
  5.         int n=input.nextInt();
  6.         int m=input.nextInt();
  7.         long[][] methods=new long[102][102];//methods[i] [j] 表示马从（1,1）跳到（i，j）的走法种数。
  8.         int i,j;
  9.         //初始状态
  10.         methods[1][1]=0;
  11.         methods[2][3]=1;
  12.         methods[3][2]=1;
  13.  
  14.     	for(i=1;i<=n;i++){
  15.     		for(j=1;j<=m;j++){
  16.     			if(i-2>=1&&j-1>=1){
  17.     				methods[i][j]+=methods[i-2][j-1];//马从（i-2,j-1）跳到（i,j），则点（i,j）的走法加上（i-2,j-1）的走法数
  18.         			methods[i][j]%=1000000007;//每次更新methods的值时，都进行取余运算，如果全部运算完再做取余运算，数字容易溢出
  19.     			}
  20.     			if(i-1>=1&&j-2>=1){
  21.     				methods[i][j]+=methods[i-1][j-2];//马从（i-1,j-2）跳到（i,j）
  22.         			methods[i][j]%=1000000007; 
  23.     			}
  24.     			if(i-1>=1&&j+2<=m){
  25.     				methods[i][j]+=methods[i-1][j+2];//马从（i-1,j+2）跳到（i,j）
  26.         			methods[i][j]%=1000000007; 
  27.     			}
  28.     			if(i-2>=1&&j+1<=m){
  29.     				methods[i][j]+=methods[i-2][j+1];//马从（i-2,j+1）跳到（i,j）
  30.         			methods[i][j]%=1000000007; 
  31.     			}
  32.     		}
  33.     	}
  34.         //methods[n][m]表示马从（1，1）到（n，m）点的走法数
  35.     	System.out.println(methods[n][m]);
  36.  
  37.     }
  38. }

进击的青蛙

分析：

  • 跟爬楼梯的题目类似，照着写，然后根据题目的具体要求再修改一下即可
  • BufferedReader类相对于 Scanner 类，这种方法会占用更少的内存，特别是在处理大量输入时。
  • 该题如果用Scanner，只能拿20分，内存超限
  1. package no1_1;
  2. import java.io.*;
  3.  
  4. public class Main {
  5.     public static void main(String[] args) throws NumberFormatException, IOException {
  6.     	BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
  7.     	int n = Integer.parseInt(reader.readLine());//读取一整行的字符串，然后转成int类型
  8.         int MOD = 1000000007;
  9.         long[] dp = new long[n+1];//dp数组先用来存石头，然后覆盖着存储到达该的方法数，（省点内存）
  10.         for(int i = 1; i <= n; i++) {
  11.             dp[i] = Integer.parseInt(reader.readLine());
  12.         }
  13.         //初始化
  14.         dp[1] = (dp[1] == 0) ? 1 : 0;
  15.         dp[2] = (dp[2] == 0) ? dp[1] + 1 : 0;
  16.         dp[3] = (dp[3] == 0) ? dp[1] + dp[2] + 1 : 0;
  17.         
  18.         for (int i = 4; i <= n; i++) {
  19.             if (dp[i] == 1) {//该点有石头，无法到达
  20.                 dp[i] = 0;
  21.             } else {//每次更新dp的方法数时，都要取余
  22.                 dp[i] = (dp[i-1]% MOD + dp[i-2]% MOD + dp[i-3]% MOD) % MOD;
  23.             }
  24.         }
  25.         if(dp[n]==0) {//无法到达
  26.             System.out.println("No Way!");
  27.         }else {//输出到达该点的方法数
  28.             System.out.println(dp[n]);
  29.         }
  30.     }
  31. }

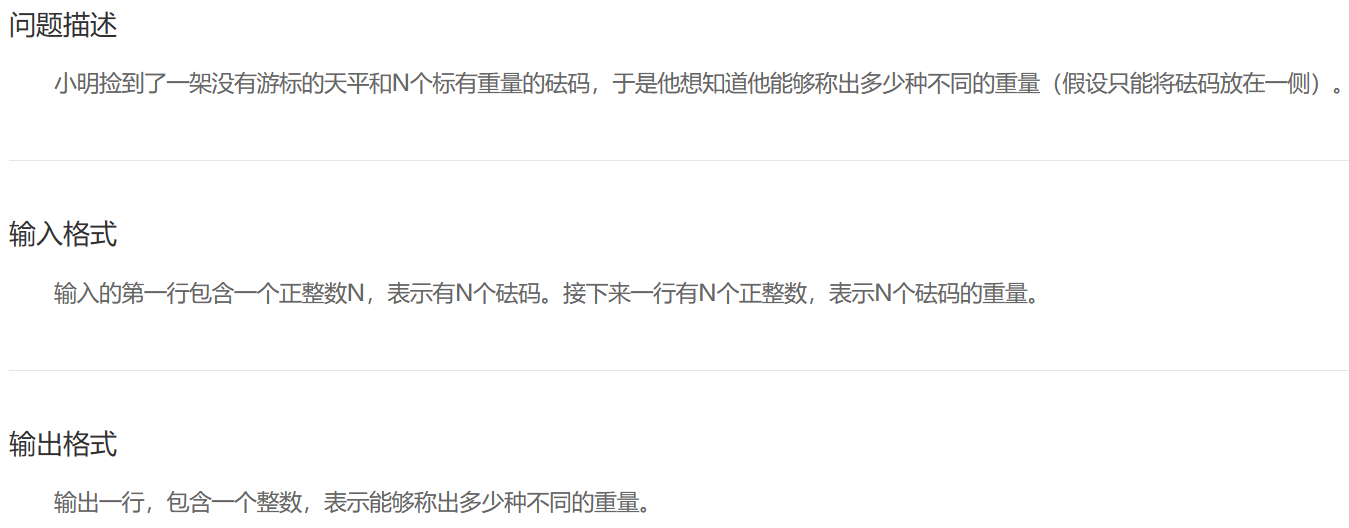
砝码称重

分析：

  •  实际上就是这堆砝码的组合问题，另外再注意称出的重量不要重复即可
  • 代码思路：

    • 创建一个布尔类型的动态规划数组dp[ ]，下标是重量，值为true时，表示是否可以称出该重量

    • 遍历每个砝码weight，判断weight ~ sum中的每个重量 i 减去weight的重量是否能称出

  1. package no1_1;
  2. import java.util.*;
  3.  
  4. public class Main {
  5.     public static void main(String[] args) {
  6.         Scanner sc = new Scanner(System.in);
  7.         int n = sc.nextInt();
  8.         int[] weights = new int[n];
  9.         for (int i = 0; i < n; i++) {
  10.             weights[i] = sc.nextInt();
  11.         }
  12.         Arrays.sort(weights); // 对重量进行排序
  13.         System.out.println(countUniqueWeights(weights));
  14.     }
  15.  
  16.     public static int countUniqueWeights(int[] weights) {
  17.     	  int sum = 0;
  18.           for (int weight : weights) {  // 计算所有砝码的总重量
  19.               sum += weight;
  20.           }
  21.  
  22.           boolean[] dp = new boolean[sum + 1];  // 创建一个布尔类型的动态规划数组，下标是重量，值表示是否可以称出该重量
  23.           dp[0] = true;  // 初始化动态规划数组的第一个元素为true，表示重量为0的情况
  24.  
  25.           for (int weight : weights) {  // 遍历每个砝码的重量
  26.               for (int i = sum; i >= weight; i--) {
  27.                   dp[i] = dp[i] || dp[i - weight];  // 使用动态规划递推式更新数组的值
  28.                   //1、dp[i]为true时，意味着i的重量已经被称出过
  29.                   //2、如果dp[i]为false时，再判断dp[i-weight]是否为true
  30.                   //3、当前要称出的目标重量为i，但当前拥有重量为weight，需要判断是否能称出剩余重量i-weight
  31.                   //4、如果dp[i-weight]为true，则(i-weight)+weight=i，则dp[i]=true
  32.                   //5、i-weight < i，所以可以查看之前的处理结果
  33.               }
  34.           }
  35.  
  36.           // 统计可以测量出的不同重量的数量
  37.           int count = 0;
  38.           for (int i = 1; i <= sum; i++) {
  39.               if (dp[i]) {
  40.                   count++;
  41.               }
  42.           }
  43.           return count;  
  44.     }
  45. }

B君的希望

问题描述

　　你有个同学叫B君，他早听闻祖国河山秀丽，列了一张所有可能爬的山的高度表，因“人往高处走”的说法，所以他希望要爬的山按照表上的顺序，并且爬的每一座山都要比前一座高，爬的山数最多，请贵系的你帮他解决这个问题。(cin,cout很坑)

输入格式

　　输入第一行为num(1~1000)和maxHeight(1~8848)，代表山的个数和最大高度
　　输入第二行有num个整数，代表表上每座山的高度height(1~maxHeight)

输出格式

　　输出只有一个数，为符合要求的最大爬山数

样例输入

10 10
8 6 8 5 9 5 2 7 3 6 3 4

样例输出

3

样例输入

10 20
8 19 9 10 3 3 15 3 10 6

样例输出

4

数据规模和约定

　　num(1~1000)，maxHeight(1~8848)，height(1~maxHeight)，都是正整数

分析：

  • dp[i]表示最高高度为height[i]的最长序列元素个数

  • 当前位置的山，只需要找到前面比它矮的山中序列最长的，再加上本身这一座山，即得最高高度为当前这座山的最长序列个数

  1. import java.util.*;
  2.  
  3. public class Main {
  4.     public static void main(String[] args) {
  5.         Scanner scanner = new Scanner(System.in);
  6.         int num = scanner.nextInt();
  7.         int maxHeight=scanner.nextInt();
  8.         scanner.nextLine();
  9.         int[] height=new int[num];
  10.         int[] dp=new int[num];//dp[i]表示最高高度为height[i]的最长序列元素个数
  11.         for(int i=0;i<num;i++) {
  12.         	height[i]=scanner.nextInt();
  13.         }
  14.         dp[0] = 1;
  15.         for (int i = 1; i < num; i++) {
  16.             dp[i] = 1; // 初始化为1，表示当前山峰本身构成一个递增序列，即最少也是爬当前这一座山
  17.             for (int j = 0; j < i; j++) {
  18.                 if (height[j] < height[i]) {
  19.                     dp[i] = Math.max(dp[i], dp[j] + 1); // 更新dp[i]为最长递增序列长度
  20.                 }
  21.             }
  22.         }
  23.         Arrays.sort(dp);//从小到大排序
  24.         System.out.println(dp[num-1]);
  25.     }
  26. }

1108: 守望者的逃离

题目描述
恶魔猎手尤迫安野心勃勃.他背叛了暗夜精灵，率深藏在海底的那加企图叛变：守望者在与尤迪安的交锋中遭遇了围杀.被困在一个荒芜的大岛上。为了杀死守望者，尤迪安开始对这个荒岛施咒，这座岛很快就会沉下去，到那时，刀上的所有人都会遇难：守望者的跑步速度，为17m/s， 以这样的速度是无法逃离荒岛的。庆幸的是守望者拥有闪烁法术，可在1s内移动60m，不过每次使用闪烁法术都会消耗魔法值10点。守望者的魔法值恢复的速度为4点/s，只有处在原地休息状态时才能恢复。

现在已知守望者的魔法初值M，他所在的初始位置与岛的出口之间的距离S，岛沉没的时间T。你的任务是写一个程序帮助守望者计算如何在最短的时间内逃离荒岛，若不能逃出，则输出守望者在剩下的时间内能走的最远距离。注意:守望者跑步、闪烁或休息活动均以秒(s)为单位。且每次活动的持续时间为整数秒。距离的单位为米(m)。

输入格式
输入仅一行，包括空格隔开的三个非负整数M，S，T。

输出格式
输出包含两行:

第1行为字符串"Yes"或"No" (区分大小写)，即守望者是否能逃离荒岛。

第2行包含一个整数，第一行为"Yes" (区分大小写）时表示守望着逃离荒岛的最短时间

第一行为"No" (区分大小写) 时表示守望者能走的最远距离。

样例输入
39 200 4
样例输出
No
197

每秒的当前总位移是选择闪烁（分为位移和休息）和选择跑步两者间的最大值

  1. package no1_1;
  2. import java.util.Scanner;
  3.  
  4. public class Main {
  5.     public static void main(String[] args) {
  6.         Scanner scanner = new Scanner(System.in);
  7.  
  8.         int M = scanner.nextInt(); // 守望者的魔法初值
  9.         int S = scanner.nextInt(); // 守望者所在的初始位置与岛的出口之间的距离
  10.         int T = scanner.nextInt(); // 岛沉没的时间
  11.  
  12.         int[] move = new int[T + 1]; // 当前这一秒选择跑步后的总位移
  13.         int[] blink = new int[T + 1]; // 当前这一秒选择闪烁后的总位移
  14.         int[] maxLen = new int[T + 1]; // 当前这一秒总位移的最优解
  15.  
  16.         //每秒的当前总位移是选择闪烁（分为位移和休息）和选择跑步两者间的最大值
  17.         for (int i = 1; i < T + 1; i++) {
  18.             move[i] = maxLen[i - 1] + 17; // 跑步，随时可以开跑，但闪烁需要蓝量支持
  19.             if (M >= 10) {
  20.                 // 有蓝就blink
  21.                 blink[i] = blink[i - 1] + 60;
  22.                 M -= 10;
  23.             } else {
  24.                 // 没蓝就rest
  25.                 blink[i] = blink[i - 1];
  26.                 M += 4;
  27.             }
  28.             maxLen[i] = Math.max(move[i], blink[i]); // 注意这并非局部最优解
  29.             if (maxLen[i] >= S) {
  30.                 System.out.println("Yes");
  31.                 System.out.println(i);
  32.                 return;
  33.             }
  34.         }
  35.         System.out.println("No");
  36.         System.out.println(maxLen[T]);
  37.     }
  38. }

1174: 计算直线的交点数

题目描述
平面上有n条直线，且无三线共点，问这些直线能有多少种不同交点数。
比如,如果n=2,则可能的交点数量为0(平行)或者1(不平行)。

输入格式
输入数据包含多个测试实例,每个测试实例占一行,每行包含一个正整数n（n<=20）,n表示直线的数量.

输出格式
每个测试实例对应一行输出，从小到大列出所有相交方案，其中每个数为可能的交点数,每行的整数之间用一个空格隔开。

样例输入
2
3
样例输出
0 1
0 2 3

分析：

  •  将n条直线排成一个序列，直线2和直线1最多只有一个交点，直线3和直线1和直线2最多有两个交点......直线n和其他n-1条直线最多有n-1个交点,由此得出n条直线互不平行且无三线共点的最多交点数：max=1+2+...+(n-1)=n(n-1)/2

  • m条直线的交点方案数：
    =（m-r）条平行线与r条直线交叉的交点数 + r条直线本身的交点方案 
    =（m-r）* r + r条之间本身的交点方案数（0<=r<m）

    m-r条平行线无交点

  1. import java.util.*;
  2.  
  3. public class Main {
  4.     public static void main(String[] args) {
  5.         int[][] dp = new int[21][200];//dp[i][j]==1表示i条直线可以有j个交点，dp[i][j]==0表示i条直线不可能有j个交点
  6.  
  7.         for (int i = 1; i < 21; i++) {//i条直线
  8.             dp[i][0] = 1;//i条直线有0个交点
  9.             for (int j = 1; j < i; j++) {
  10.                 int n = i - j; // j条直线平行，n条直线不平行于j条直线，然后查找n条直线的交点数
  11.                 for (int k = 0; k <= n * (n - 1) / 2; k++) {//n条直线互不平行且无三线共点的最多交点数:n(n-1)/2
  12.                     if (dp[n][k] == 1) { // 寻找i-j条直线内部交点种类
  13.                         dp[i][k + j * n] = 1; // k+j*m为总的交点种类
  14.                     }
  15.                 }
  16.             }
  17.         }
  18.  
  19.         //打印输出
  20.         Scanner scanner = new Scanner(System.in);
  21.         while (scanner.hasNext()) {
  22.             int n = scanner.nextInt();
  23.             System.out.print("0");
  24.             for (int i = 1; i <= n * (n - 1) / 2; i++) {
  25.                 if (dp[n][i] == 1) {
  26.                     System.out.print(" " + i);
  27.                 }
  28.             }
  29.             System.out.println();
  30.         }
  31.  
  32.         scanner.close();
  33.     }
  34. }

1191: 化学品问题

题目描述
一个实验室有N个放化学品的试管，排列在一条直线上。如果连续M个试管中放入药品，则会发生爆炸，于是，在某些试管中可能不放药品。
任务：对于给定的N和M，求不发生爆炸的放置药品的方案总数

输入格式
第一行是一个正整数L，代表输入数据的组数
接下来L行，每行有两个正整数N，M( 1＜N＜32，2≤M≤5)

输出格式
输出L行，每行只有一个正整数S，表示对应输入数据的方案总数。

样例输入
2
4 3
3 2
样例输出
13
5

 分析：

  • 分三种情况：
  • 1、n<m：随便放，对于每个试管，都有放或不放药品两种选择，所以方案数为2*2*……，累乘
  • 2、n==m：随便放，再减去一种连续放m个的情况
  • 3、n>m：随便放，再减去会爆炸的情况。
    • 爆炸的情况为：i-1的最后m支试管的第一支没放药，之后的m-1支连续放药，同时，到i时添加的试管放药了
  1. import java.util.Scanner;
  2.  
  3. public class Main {
  4.     public static void main(String[] args) {
  5.         Scanner scanner = new Scanner(System.in);
  6.         int l = scanner.nextInt();
  7.  
  8.         while (l-- > 0) {
  9.             int n = scanner.nextInt();
  10.             int m = scanner.nextInt();
  11. 			long[] dp = new long[50];//dp[i]表示i支试管可行方案数
  12.             dp[0] = 1;//试管都不放药品
  13.  
  14.             for (int i = 1; i <= n; i++) {
  15.                 if (i < m) {//随便放
  16.                     dp[i] = 2 * dp[i - 1];
  17.                 }
  18.                 if (i == m) {//随便放，再减去一种连续放m个的情况
  19.                     dp[i] = 2 * dp[i - 1] - 1;
  20.                 }
  21.                 if (i > m) {//随便放，再减去会爆炸的情况
  22.                     dp[i] = 2 * dp[i - 1] - dp[i - m - 1];
  23.                 }
  24.             }
  25.  
  26.             System.out.println(dp[n]);
  27.         }
  28.     }
  29. }

1193: 半数集问题

题目描述
给定一个自然数n，由n开始可以依次产生半数集set(n)中的数如下。
(1) n∈set(n)；
(2) 在n的左边加上一个自然数，但该自然数不能超过最近添加的数的一半；
(3) 按此规则进行处理，直到不能再添加自然数为止。
例如，set(6)={6,16,26,126,36,136}。半数集set(6)中有6 个元素。
注意半数集是多重集。

编程任务：
对于给定的自然数n，编程计算半数集set(n)中的元素个数。

输入格式
输入数据m行，每行给出一个整数n。(0〈n〈1000)

输出格式
输出只有m行，每行给出半数集set(n)中的元素个数。

样例输入
6
99
样例输出
6
9042

分析：

  • 存在大量可重复利用的结果
  • 利用记忆化搜索 
  1. import java.util.Scanner;
  2.  
  3. public class Main {
  4.     public static void main(String[] args) {
  5.         Scanner scanner = new Scanner(System.in);
  6.         while(scanner.hasNext()) {
  7.         	int n=scanner.nextInt();
  8.         	long []a=new long[1000];//a[i]表示i的半数集个数
  9.             a[1]=1;
  10.             int sumA=1;//n这个数本身也算一种
  11.             for (int i =1; i <=n/2; i++) {
  12.                 int sum=0;//sum表示i的半数集个数
  13.                 for (int j =1; j <=i/2; j++) {
  14.                     sum+=a[j];
  15.                 }
  16.                 a[i]=sum+1;
  17.                 sumA+=a[i];
  18.             }
  19.             a[n]=sumA;
  20.             System.out.println(a[n]);
  21.         }
  22.     }
  23. }

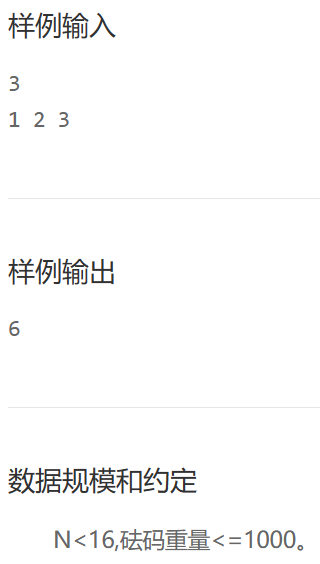
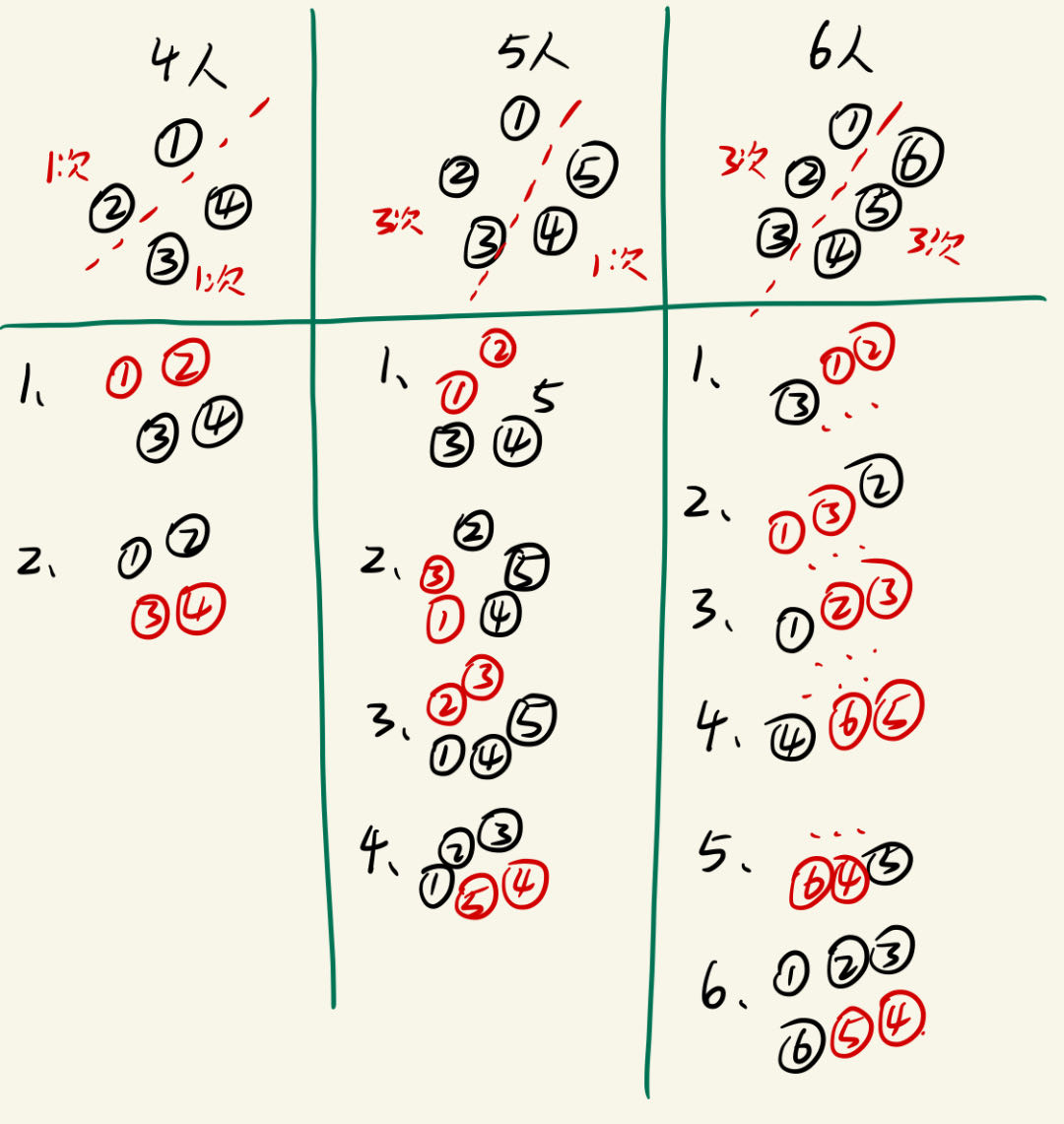
1217: 换位置

题目描述
M个人围成一圈，每分钟相邻的两个人可以交换位置（只能有一对交换）。求使M个人的顺序颠倒（即每个人左边相邻的人换到右边，右边相邻的人换到左边）所需的最少时间（分钟数）。

输入格式
第一行为测试数据的组数n，以后n行中每行为一个小于32767的正整数，表示M

输出格式
对于每组测试数据，输出一个数，表示最少需要的分钟数。

样例输入
3
4
5
6
样例输出
2
4
6
 

分析：

  • 观察上述例子，可猜想得到规律：
    • 把圈子划成左右两半，左半边的人走左半边的道最近，右边人的走右边
    • 不断细分，后面的结果与前面的结果息息相关，所以该题用动态规划做
    • （实际上，结果符合斐波那契数列的规律，也可从该点入手）
  1. import java.util.Scanner;
  2.  
  3. public class Main {
  4. 	public static void main(String[] args) {
  5.         Scanner scanner = new Scanner(System.in);
  6.         int n=scanner.nextInt();
  7.         int[] dp=new int[32767];
  8.         dp[1]=0;
  9.         dp[2]=1;
  10.         dp[3]=3;
  11.         for(int i=4;i<32767;i++) {//把人群划分成两半进行交换
  12.         	if(i%2==0) {//偶数个人
  13.         		dp[i]=dp[i/2]+dp[i/2];
  14.         	}else {//奇数个人
  15.         		dp[i]=dp[i/2]+dp[i/2+1];
  16.         	}
  17.         }
  18.         while(n-->0) {
  19.         	int m=scanner.nextInt();
  20.         	System.out.println(dp[m]);
  21.         }
  22.     }
  23. }

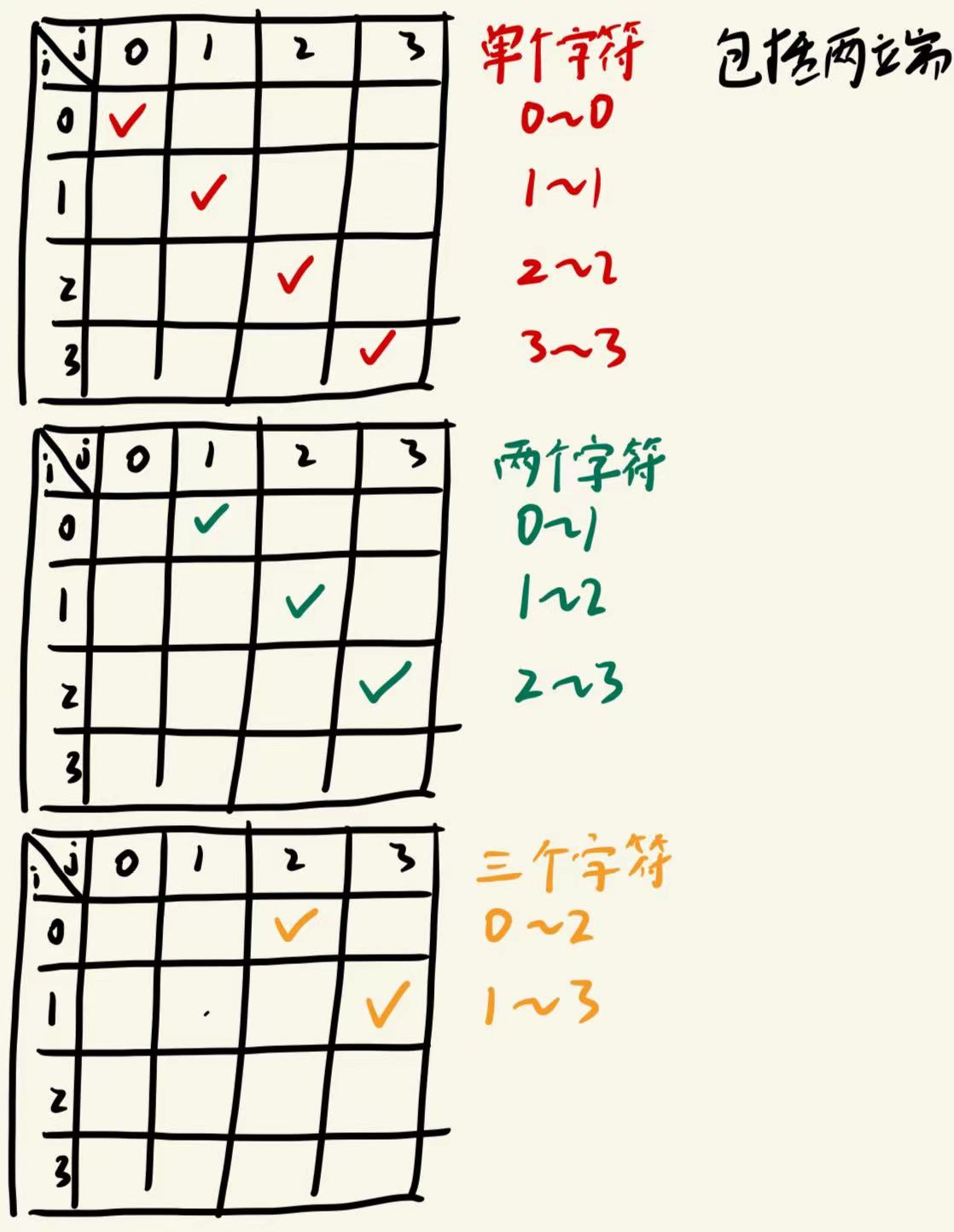
5、最长回文串

给你一个字符串 s，找到 s 中最长的 回文子串

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

提示：

  • 1 <= s.length <= 1000
  • s 仅由数字和英文字母组成

  1. class Solution {
  2.     public String longestPalindrome(String s) {
  3.         if (s == null || s.length() == 0) {
  4.             return "";
  5.         }
  6.         
  7.         int n = s.length();
  8.         //dp[i][j]表示从索引i到索引j（包括两端）的子串是否为回文串
  9.         boolean[][] dp = new boolean[n][n];
  10.         int start = 0;
  11.         int maxLength = 1;
  12.         
  13.         // 单个字符都是回文串
  14.         for (int i = 0; i < n; i++) {
  15.             dp[i][i] = true;
  16.         }
  17.         
  18.         // 两个字符的情况
  19.         for (int i = 0; i < n - 1; i++) {
  20.             if (s.charAt(i) == s.charAt(i + 1)) {
  21.                 dp[i][i + 1] = true;
  22.                 start = i;
  23.                 maxLength = 2;
  24.             }
  25.         }
  26.         
  27.         // 三个及以上字符的情况
  28.         for (int len = 3; len <= n; len++) {
  29.             for (int i = 0; i < n - len + 1; i++) {
  30.                 int j = i + len - 1;
  31.                 //检查当前子串的两端字符是否相等，并且判断去掉两端字符后的子串是否为回文串
  32.                 if (s.charAt(i) == s.charAt(j) && dp[i + 1][j - 1]) {
  33.                     dp[i][j] = true;
  34.                     start = i;
  35.                     maxLength = len;
  36.                 }
  37.             }
  38.         }
  39.         
  40.         return s.substring(start, start + maxLength);
  41.     }
  42. }

10、正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

  • '.' 匹配任意单个字符
  • '*' 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

 

示例 1：

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

示例 2:

输入：s = "aa", p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3：

输入：s = "ab", p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

提示：

  • 1 <= s.length <= 20
  • 1 <= p.length <= 20
  • s 只包含从 a-z 的小写字母。
  • p 只包含从 a-z 的小写字母，以及字符 . 和 *。
  • 保证每次出现字符 * 时，前面都匹配到有效的字符

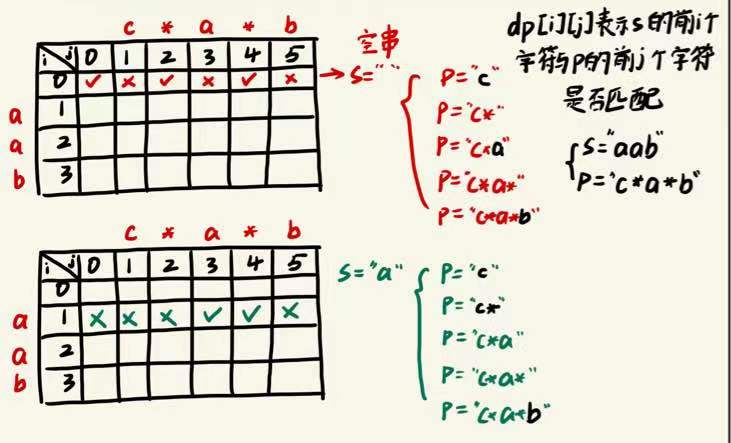
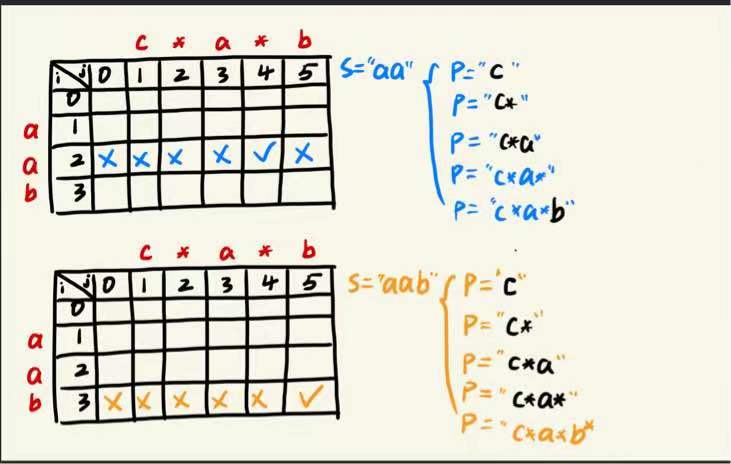
分析：

  1. class Solution {
  2.     public boolean isMatch(String s, String p) {
  3.         int m = s.length();
  4.         int n = p.length();
  5.         // 创建动态规划数组，dp[i][j] 表示 s 的前 i 个字符与 p 的前 j 个字符是否匹配
  6.         boolean[][] dp = new boolean[m + 1][n + 1];
  7.  
  8.         // 初始状态：空字符串与空模式匹配
  9.         dp[0][0] = true;
  10.  
  11.         // 初始化第一行：空字符串与模式的匹配情况
  12.         for (int j = 1; j <= n; j++) {
  13.             // 当 p 的当前字符为 '*' 时，表示可以忽略该字符和前一个字符，因此取值为 j-2 的状态
  14.             if (p.charAt(j - 1) == '*') {
  15.                 dp[0][j] = dp[0][j - 2];
  16.             }
  17.         }
  18.  
  19.         // 填充dp数组
  20.         for (int i = 1; i <= m; i++) {
  21.             for (int j = 1; j <= n; j++) {
  22.                 // 当前字符匹配或者 p 的当前字符为 '.' 时，取决于前一个字符的匹配状态
  23.                 if (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.') {
  24.                     dp[i][j] = dp[i - 1][j - 1];
  25.                 } else if (p.charAt(j - 1) == '*') {
  26.                     // 当前字符为 '*' 时，有两种情况：
  27.                     // 1. 忽略当前字符和前一个字符，即取值为 j-2 的状态
  28.                     dp[i][j] = dp[i][j - 2];
  29.                     // 2. 当前字符匹配前一个字符（或者前一个字符为 '.'），取决于当前字符与前一个字符匹配的状态
  30.                     if (p.charAt(j - 2) == '.' || p.charAt(j - 2) == s.charAt(i - 1)) {
  31.                         dp[i][j] = dp[i][j] || dp[i - 1][j];
  32.                     }
  33.                 }
  34.             }
  35.         }
  36.         return dp[m][n];
  37.     }
  38. }

 

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/天景科技苑/article/detail/870530
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号