入门：“A Survey on Multi-view Learning” 辅助学习（中）_gpy.models.sgplvm

写在前面：

不知道是由于作者电脑原因还是csdn的原因，在试图一次性上传这篇论文时卡爆了，事实上即便分三次也很卡，简单的说，本篇论文的辅助阅读分三次上传：

上篇是这篇论文的前四章之前

中篇是5-7章，也是个人认为比较重要的部分

下篇是后三章+总结

希望查看的各位大佬按需选择，如果有出错之处也欢迎大家指正与讨论，写这个辅助学习一个是记录一下自己的学习过程，另一个是希望能帮到读论文的你，本文仅供参考，还是看论文原文最为清晰。

---

“5. Co-training Style Algorithms” 5. 协同训练风格算法

协同训练（Blum 和 Mitchell，1998）是最早的多视图学习方案之一。从那时起，开发了许多变体。除了设计各种算法的研究之外，还有大量关于协同训练假设的工作，这保证了算法的成功。

“5.1 Assumptions for Co-training” 5.1 协同训练的假设

协同训练考虑这样一种环境，其中每个示例可以分为两个不同的视图，并做出三个主要假设：

（a）充分性：每个视图本身足以进行分类

（b）兼容性：两个视图中的目标函数以高概率预测同时出现的特征的相同标签，以及

（c）条件独立性：给定类标签，视图是条件独立的。条件独立性假设起着至关重要的作用，但它通常太强而在实践中无法满足，因此考虑了几种较弱的替代方案。

“5.1.1 Conditional Independence Assumption”  5.1.1 条件独立假设

Blum 和 Mitchell (1998) 证明，当两个足够的视图在给定类别标签的情况下条件独立时，协同训练可以成功。

他们给出了一个定理，尽管存在分类噪声，如果视图 X1,2 上的概念类 C1,2 在 PAC 模型中是可学习的，并且如果满足条件独立性假设，则 (C1, C2) 在仅根据未标记数据训练的协同训练模型中是可学习的，给定初始弱有用预测变量 h(x1)。

具体来说，让分类噪声 (α, β) 为这样的设置，其中真实的正例被错误地（独立地）标记为概率 α，真实的负例被错误地（独立地）标记为概率 β。再次将 f (x) 定义为目标概念，并将 p = PrD(f (x) = 1) 定义为 D 中的随机示例为正的概率。两个噪声率之和满足

概率最多为 1 − 4ε2。

上述不等式为基于规则的引导的协同训练限制提供了一定程度的合理性。然而，它并没有提供泛化误差作为经验可测量量的函数的界限；因此，基于相同的条件独立假设，Dasgupta 等人(2002) 给出了协同训练的 PAC 风格界限。令 S 为由各个样本 s1、····、sm 组成的 i.i.d 样本。数据集 X 上的部分规则 h 是从 X 到标签集 {1,···,k,⊥} 的映射，其中 k 是类标签的数量，⊥ 表示部分规则 h 不给出任何意见。然后，对于概率至少为 1 − δ 的 S 的选择，对于所有规则h1 和 h2，我们有以下结果：如果对于 1 ≤ i ≤ k ，γi(h1, h2, δ/2) > 0，则 f 是一个排列，且对于所有 1 ≤ i ≤ k，

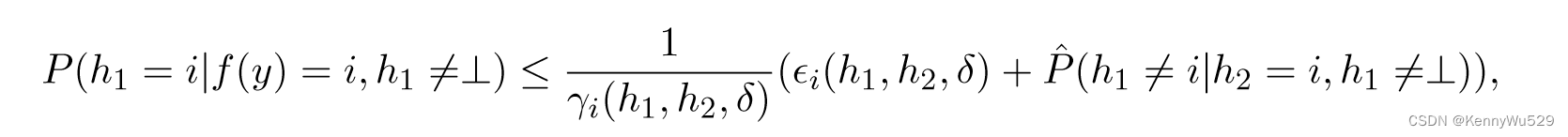
其中

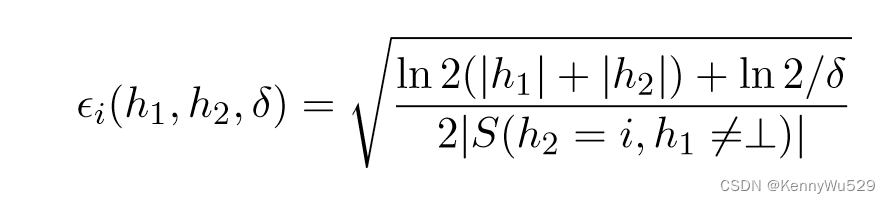
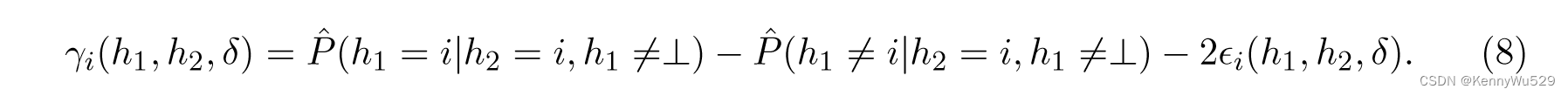
请注意，如果样本量足够大（相对于 |h1| 和 |h2|），则 ϫi(h1, h2, δ) 接近于零。另请注意，如果 h1 和 h2 几乎完全一致，且两者都不是 ⊥，则 γi(h1, h2, δ) 接近 1。 h1 和 h2 之间的一致性限制了 h1 误差的上限。因此，协同训练算法需要在条件依赖假设下最大化基于不同视图的分类器之间对未标记数据的一致性，以提高每个假设的准确性。

“5.1.2 Weak Dependence Assumption”  5.1.2 弱依赖假设

上述条件独立性假设对于实际应用中的两种视图来说过于强烈而无法满足。 Abney（2002）放宽了假设，发现仅弱依赖性就可以导致成功的协同训练。给定映射函数 Y = y，相反视图规则 h1 和 h2 的条件依赖定义为

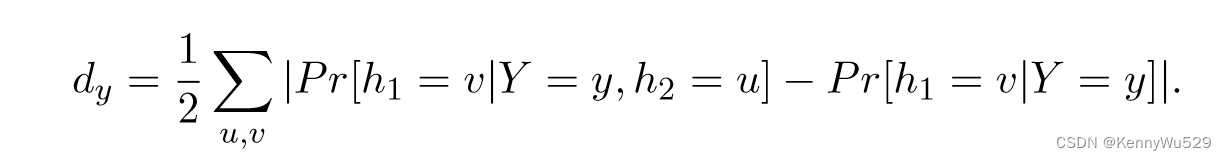
如果 h1 和 h2 条件独立，则 dy = 0。 以防万一，h1 和 h2 满足弱规则依赖：

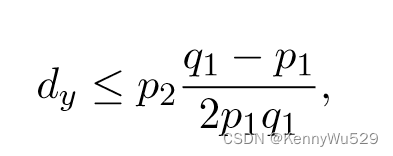其中 p1 = minu Pr[h2 = u|Y = y]，p2 = minu Pr[h1 = u|Y = y]，并且 q1 = 1 − p1。

“5.1.3 Expansion Assumption” 5.1.3 扩展假设

巴尔坎等人 (2004) 对底层数据分布提出了一个弱得多的“扩展”假设，并证明只要在每个特征集上有适当强大的 PAC 学习算法，迭代协同训练就足以成功。

假设样本是从实例空间 X 上的分布 D 中抽取的。令 X+ 和 X− 分别表示 X 的正区域和负区域。对于 S1 ⊆ X1 和 S2 ⊆ X2，设 Si(i = 1, 2) 表示示例 <x1, x2> 具有 xi ∈ Si  的事件。如果我们将 S1 和 S2 视为每个视图中的置信集，则 Pr(S1 ∧ S2) 表示我们对两个视图都有信心的示例的概率质量，Pr(S1 ⊕ S2) 表示示例上的概率质量我们仅对一种视图有信心的例子。

扩展假设：

定义 D+ 正在扩展:如果对于任何 S1 ⊆ X1+ 和 S2 ⊆X2+，

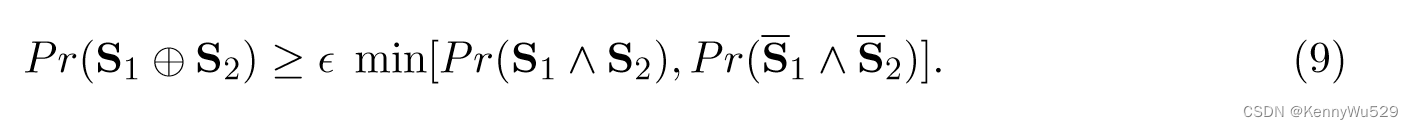
另一种稍强的扩展称为“左右扩展 left-right expansion” ，可以定义如下。

D+ 是右展开的:如果对于任何 S1 ⊆ X1+ 和 S2 ⊆X2+，若

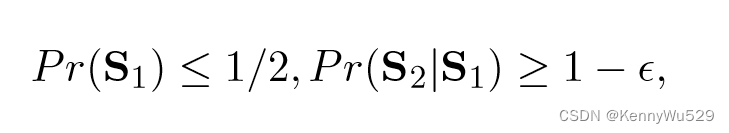
则

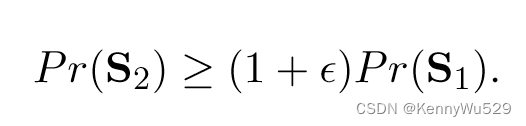
如果上面的索引 1 和 2 颠倒，假设成立，则 D+ 是左扩展的。

可以清楚地看出，如果 Si  是 Xi+ 中的置信集，并且该集很小（Pr(Si) ≤ 1/2），则一个分类器从服从 Si 在 X3−i (i = 1, 2) 上诱导的条件分布的正数据中学习，被训练直到它在该分布上的误差error ≤ ε 。该定义意味着 X3−i 上的置信集将比 Si 具有明显更大的概率，因此很清楚为什么这对于协同训练有用。

“5.1.4 Large Diversity Assumption” 5.1.4 大多样性假设

Goldman 和 Zhou (2000) 使用了两种不同的监督学习算法，Zhou 和 Li (2005b) 使用了同一基学习器的两种不同参数配置来进行没有冗余视图的协同训练式算法，但他们都没有阐述他们成功的原因。随后，Wang 和 Zhou（2007）表明，当两个学习器之间的多样性大于它们的误差时，可以通过协同训练式算法来提高学习器的性能。两个分类器 hi 和 hj 之间的差异 d(hi, hj) 意味着它们之间不同的偏差，并且两个分类器将用不同的标签来标记一些实例。如果分类器 hi 标记的样本对于分类器 hj 有用，那么 hi 应该知道一些 hj 不知道的信息。换句话说，hi 和 hj 应该有显着差异。随着协同训练过程的进行，两个分类器将变得越来越相似，并且随着两个分类器为彼此标记越来越多的未标记实例，它们之间的差异将变得越来越小。因此，经过多轮学习后，协同训练过程不会进一步提高性能。

“5.2 Co-training” 5.2 协同训练

协同训练最初是针对半监督学习问题提出的，其中可以访问标记数据和未标记数据。它考虑了一种设置，其中每个示例都可以分为两个不同的视图，并为其成功做出三个主要假设：充分性、兼容性和条件独立性。

在原始协同训练算法中（Blum 和 Mitchell，1998），给定一组标记示例 L 和一组未标记示例 U，该算法首先创建一个包含 u 个未标记示例的较小池 U '。然后它会迭代以下过程。

首先，使用 L 分别在视图 x1 和 x2 上训练两个朴素贝叶斯分类器 h1 和 h2。其次，允许这两个分类器中的每一个都检查未标记的集合 U ' 并将其最有把握标记为正的 p 个示例和最有把握将其标记为负的 n 个示例添加到 L 中，以及相应分类器分配的标签。最后，通过从 U 中随机抽取 2p + 2n 个示例来补充池 U '。

“5.3 Co-EM”

协同训练算法背后的直觉是分类器 h1 将示例添加到标记集中，然后分类器 h2 将能够使用该示例进行学习。如果条件独立性假设成立，那么平均而言，每个添加的示例都将与随机示例一样提供信息，并且学习应该取得进展，但会添加许多属于错误类别的示例。如果违反独立性假设，那么平均而言，添加的示例信息量将较少，并且协同训练可能不会成功。因此，我们没有为未标记的示例提交标签，而是选择在每个视图中运行 EM，并为未标记的示例提供可能从一次迭代到另一次迭代的概率标签。这是 co-EM（Nigam 和 Ghani，2000）的主要思想。

对于许多问题，Co-EM 的性能优于协同训练，但它需要算法处理概率标记的训练数据，并需要分类器输出类别概率。因此，尽管已知支持向量机 (SVM) 能够更好地适应许多分类问题的特征，但仅以朴素贝叶斯作为基础学习器来研究 co-EM 算法。通过以概率方式重新表述 SVM 并用概率估计未标记数据的标签，Brefeld 和 Scheffer (2004) 成功开发了 SVM 的 co-EM 版本来缩小这一差距。

“5.4 Co-regularization” 5.4 共正则化

假设我们有两个假设空间 H1 和 H2，每个假设空间都包含一个很好地逼近目标函数的预测变量。在协同训练的情况下，这两者是在数据的不同表示或“视图”上定义的，并交替训练以最大程度地提高对未标记示例的相互一致性。

最近，几篇论文将这些直觉表述为 H1 和 H2 之间的联合复杂性正则化或共同正则化（Sindhwani 等人，2005 年；Sindhwani 和 Rosenberg，2008 年），H1 和 H2 被视为在输入空间 X 上定义函数的再现核希尔伯特空间“Reproducing Kernel Hilbert Spaces” （RKHSs）。

给定一些标记示例 (xi, yi)i∈L 和一组未标记数据 {xi}i∈U ，共正则化学习预测函数，

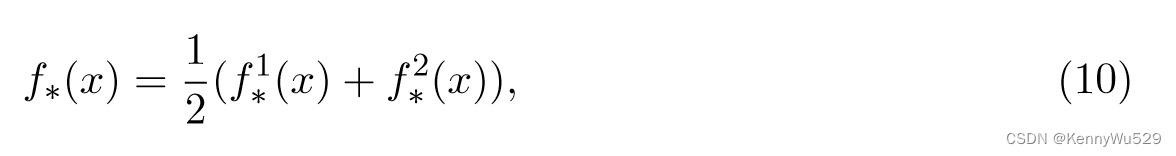
其中 f*1 ∈ H1 和 f*2 ∈ H2 通过求解以下优化问题得到，

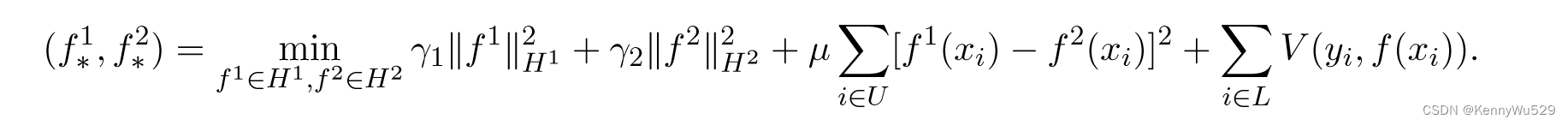
在此目标函数中，前两项分别通过 H1 和 H2 中的 RKHS 范数 ‖ · ‖2H1 和 ‖ · ‖2H2 衡量复杂性，第三项强制预测变量之间对未标记示例的一致性，最后一项评估标记数据上关于损失函数 V (·,·) 的平均函数 f − (f 1 + f 2)/2。实值参数 γ1、γ2 和 μ 允许正则化项之间进行不同的权衡。 L 和 U 分别是标记和未标记示例的索引集。

“5.5 Co-regression” 5.5 协回归

大多数多视图和半监督学习的研究都集中在分类问题上，回归问题也可以用类似的方式解决。例如，Zhou 和 Li (2005a) 开发了一种名为 CoREG 的协同训练式半监督回归算法。该算法采用两个 k 最近邻 (kNN) 回归器，每个回归器在学习过程中为另一个回归器标记未标记的数据。为了选择合适的未标记示例进行标记，CoREG 通过参考未标记示例的标记对标记示例的影响来估计标记置信度。最终预测是通过对两个回归器生成的回归估计进行平均来做出的。

受共同正则化算法的启发，Brefeld 等人 (2006)提出了一种协回归算法。正式给出 M 个视图，训练实例 {Xv}Mv=1 ，标签为 y(x) ∈ R，以及标签未知的有限实例集 Z ⊆ X，我们尝试找到最小化

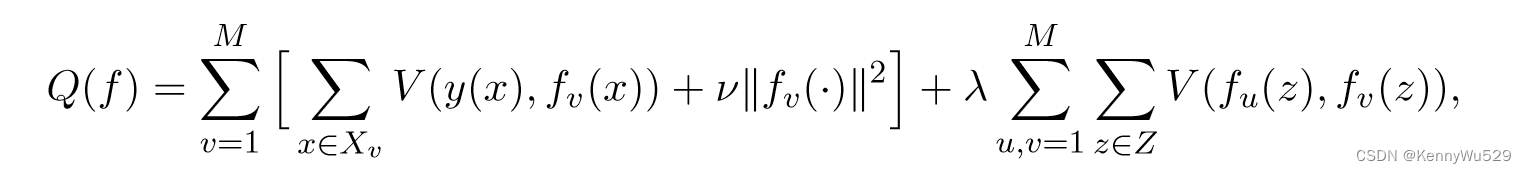
的 f1 : X → R, ···，fM：X → R。

其中衡量复杂性的范数位于各自的希尔伯特空间中，V (y(x), fv(x)) 评估预测变量和标记示例的目标值之间的损失，并且 V (fu(z), fv(z))强加了未标记的示例的预测变量之间的一致性。

“5.6 Co-clustering” 5.6 共聚类

协同训练算法最初是为半监督学习而设计的，但协同训练的思想也可以应用于无监督和监督学习环境。假设真正的底层聚类将每个视图中的对应点分配给同一聚类，已经使用多视图方法开发了几种聚类技术。 Bickel 和 Scheffer (2004) 研究了最常用的聚类方法（例如 k-means、k-medoids 和 EM）的多视图版本。以k-means为例：在每次迭代中，在一个视图中运行k-means，然后将分区信息交换到另一个视图并再次在第二个视图中运行k-means。终止后，计算每个簇和视图的一致均值，然后将每个示例分配给通过封闭概念向量确定的一个不同簇。

考虑到谱聚类算法在任意形状的聚类上具有良好的性能并且有一个明确定义的数学框架，一些方法被设计为利用协同训练的思想来进行谱聚类（Kumar et al., 2010, 2011; Kumar and Daume ́ III, 2011）。例如，Kumar 和 Daume III (2011) 开发了一种多视图谱聚类算法，该算法在各个图上求解谱聚类，以获得每个视图中的判别特征向量 U1(U2)，然后使用 U1(U2) 对点进行聚类，使用此聚类分别修改视图 2(1) 中的图结构。该过程重复多次。

“5.7 Graph-based Co-training” 5.7 基于图的协同训练

大多数协同训练风格的算法关注如​​何最小化两个分类器之间的不一致，以获得多视图学习者满意的性能，因此这些方法可以被视为基于分歧的方法。

基于图的协同训练方法也存在；例如，Yu等人（2007，2011）提出了一种通过高斯过程（GP）进行协同训练的贝叶斯无向图模型。

假设我们对 n 个数据示例 {xi} 有 m 个不同视图，输出为 {yi}。令 fj 表示第 j 个视图的潜在函数，并令 fj ∼ GP (0, κ) 为其在视图 j 中的 GP 先验。然后引入潜在函数 fc 以确保输出 y 和 m 个视图的 m 个潜在函数 fj 之间的条件独立性。在功能层面，输出 y 仅依赖于 fc，潜在函数 fj 仅通过共识函数 fc 相互依赖。也就是说，我们有联合概率：

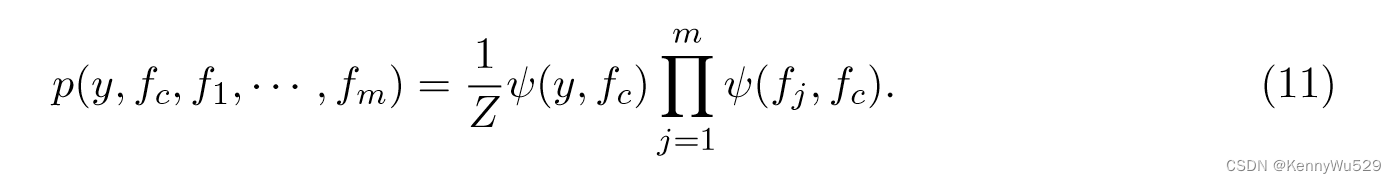
在具有 n 个数据示例xi的地面网络中，令 fc = {fc(xi)}ni=1 且 fj = {fj(xji )}ni=1。该图形模型导致以下因式分解：

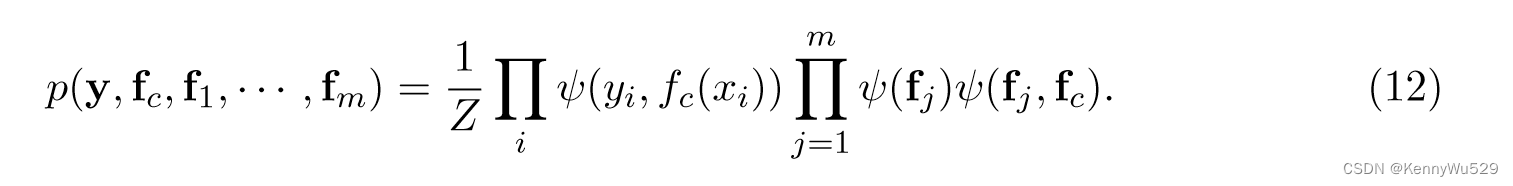
这里，视图内的势ψ(fj)指定每个视图j内的依赖结构，共识的势ψ(fj,fc)描述每个视图中的潜在函数如何与共识函数fc相关。对每个视图使用 GP 先验，我们可以定义以下潜力：

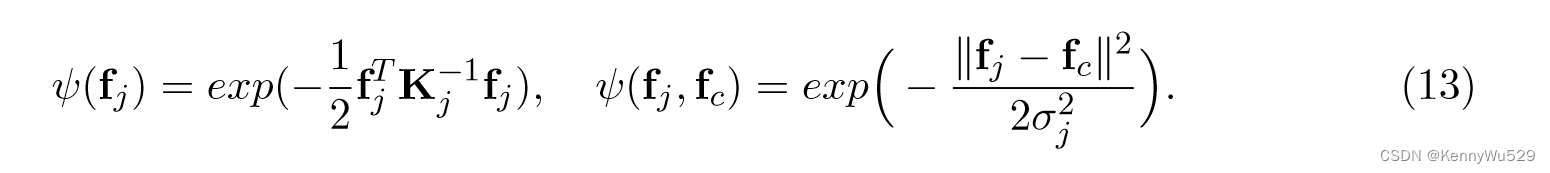
对方程 (12)中所有 m 个潜在函数进行整合，我们得到多视图学习的协同训练核为

这个协同训练内核揭示了以前不清楚的见解关于来自不同视图的内核如何在多视图学习中组合，并让我们可以简单地解决 GP 分类问题。

Wang 和 Zhou (2010) 将协同训练过程视为两种视图的组合传播，并将基于图和分歧的半监督学习统一到一个框架中：

在一个视图中，标签可以从初始标记的示例传播到未标记的示例，并且这些新标记的示例可以添加到另一视图中。然后，另一个视图可以将初始标记示例和这些新标记示例的标签传播到剩余的未标记实例。这个过程可以重复进行，直到满足停止条件。

“5.8 Multi-learner Algorithms”  5.8 多学习器算法

Goldman 和 Zhou（2000）提出了一种新的“协同训练”策略，使用未标记的数据来提高标准监督学习算法的性能。在不假设两种视图都足以实现完美分类的情况下，这种协同训练策略的唯一要求是其假设将示例空间划分为一组等价类。假设A和B是两种不同的监督算法，U是未标记数据，L是原始标记数据，LA是B为A标记的数据，LB是A为B标记的数据。在每次迭代开始时，在标记示例 L ⋃ LA 上训练 A 以获得假设 HA。同理，在L⋃LB上训练B得到HB。每个算法都会考虑其每个等价类，并决定使用哪个等价类来为其他算法标记来自 U 的数据。这种协同训练算法会重复进行，直到迭代过程中 LA 和 LB 都不会发生变化。

Zhou and Li (2005b)提出了另一种协同训练风格的半监督算法，称为三训练“tri-training” ，它不需要用足够和冗余的视图来描述实例空间，也不像Goldman和zhou（2000）那样对监督算法施加任何约束。三重训练从原始标记示例集中生成三个分类器，然后在迭代中使用未标记示例进行细化。对于每次迭代，如果其他两个分类器在某些条件下就标记达成一致，则为分类器标记一个未标记的示例。

当标记反馈样本数量较小时，传统的基于 SVM 的相关性反馈方法的性能通常较差，因此 Li 等人(2006) 开发了一种新的机器学习技术，即多重训练 SVM (MTSVM)，来缓解这个问题。 MTSVM 结合了协同训练技术和特征空间中随机采样方法的优点。然而，简单地将协同训练算法与SVM结合使用是不现实的，因为协同训练算法要求在协同训练过程开始之前初始子分类器具有良好的泛化能力。因此，作者采用分类器委员会学习“classifier committee learning” 来增强每个子分类器的泛化能力。最初，一系列特征子集 - 换句话说，数据的多个视图 - 可以使用随机子空间方法从原始输入特征中获得，然后可以在这些生成的视图上学习多个分类器，并可以在半监督相关性反馈设置环境中相互训练。最后，使用多数投票规则生成最优分类器。

分类器委员会学习是一种集成学习方法，它通过构建多个分类器来完成学习任务。每个分类器都是由不同的训练数据集训练出来的，因此它们之间具有差异性。在测试时，每个分类器都会对测试样本进行预测，最后将所有分类器的预测结果进行投票或加权投票，以决定测试样本的类别。这种方法可以有效地提高分类器的准确性和泛化能力. 与多数投票规则不同，分类器委员会学习可以生成最优分类器。因为它可以通过合理地选择和组合不同的分类器来达到最优性能.

“6. Multiple Kernel Learning” 6. 多核学习

多核学习（MKL）最初是为了控制可能的核矩阵的搜索空间容量以实现良好的生成而开发的，但它已广泛应用于涉及多视图数据的问题。这是因为 MKL 中的内核自然对应于不同的视图，适当地组合内核可以提高学习性能。 G ̈ onen 和 Alpaydın (2011) 回顾了 MKL 的文献。由于MKL可以被视为多视图学习的一部分，因此我们更重视MKL与这些部分之间的联系；在本节中，我们将阐述代表性的 MKL 算法和理论研究，以呈现本次调查的完整情况。

“6.1 Boosting Methods” 6.1 提升方法

受到集成和增强方法的启发（Duffy 和 Helmbold，2000；Friedman 等人，2001），Bennett 等人(2002) 提出了多重加性回归核 (MARK) 算法，该算法考虑由不同核函数和参数形成的大型核矩阵库。决策函数修改为

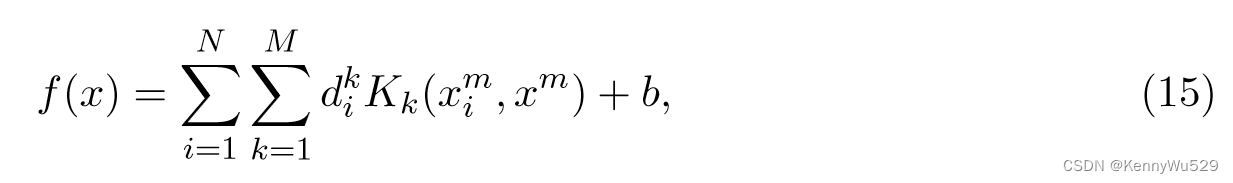
由异构核函数 K1,····,KM 的线性组合组成，每个核可以是任意类型；例如，{Kk} 可以是具有不同参数的 RBF 核。与集成方法一样，内核的每一列都被视为假设，并且内核列是动态生成的。基于梯度的集成算法，例如梯度提升，可以适应这个优化问题。

列生成（CG）技术已广泛用于求解大规模线性规划（LP）。毕等人(2004) 使用 2-范数正则化方法将 LPBoost 扩展到二次规划 (QP)，因此许多成功的公式，例如经典的 SVM、岭回归等，都可以从 CG 技术中受益。

克拉默等人 (2002) 使用 boosting 范式来执行内核构建过程。由于对 AdaBoost 及其变体的多种解释都将 boosting 过程视为尝试最小化分类错误的过程，因此可以通过重写一对示例 (x1, y1) 和 (x2, y2) 的损失函数为：

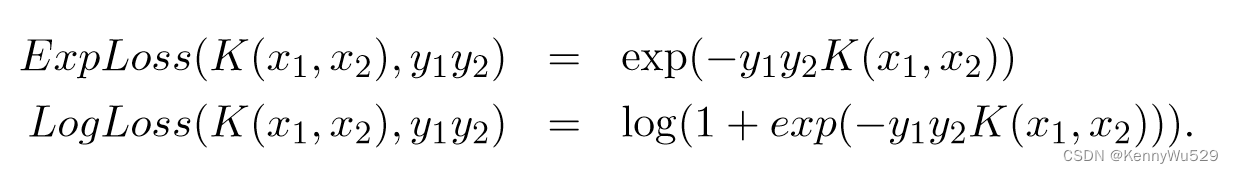
来修改 boosting 方法以与内核一起使用。

一对实例被视为单个示例，成对的相同标签被视为正标记示例，而成对的相反标签被视为负标记示例。与增强分类算法“boost algorithms for classification” 类似，可以使用这两个损失函数之一迭代更新组合核矩阵。

“6.2 Semi-Definite Programming”  6.2 半定规划

半定规划（SDP）的一般形式是

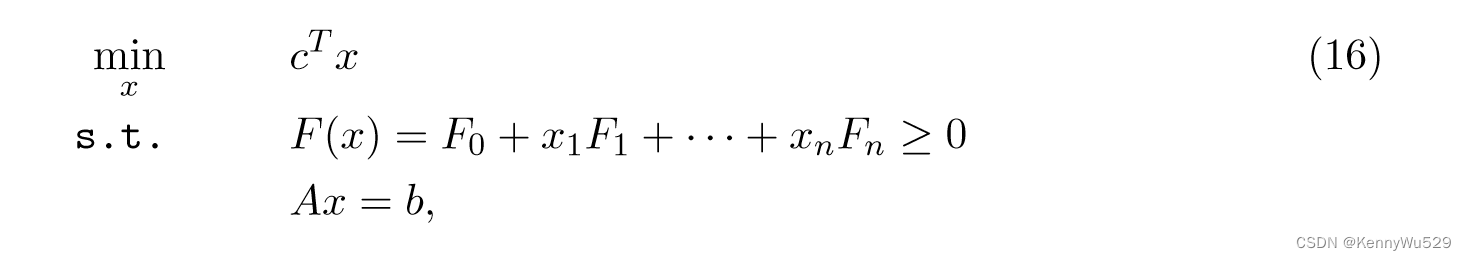其中 x ∈ Rp 且 Fi = Fi T ∈ Rp×p。

请注意，对象在未知 x 中是线性的，并且不等式和等式约束在 x 中都是线性的。

兰克里特等人 (2002, 2004) 展示了如何通过 SDP 技术从数据中学习核矩阵。特别地，如果数据的所有标签已知，则任务是找到与标签集 y 最大对齐的核矩阵 K，然后该问题被表述为

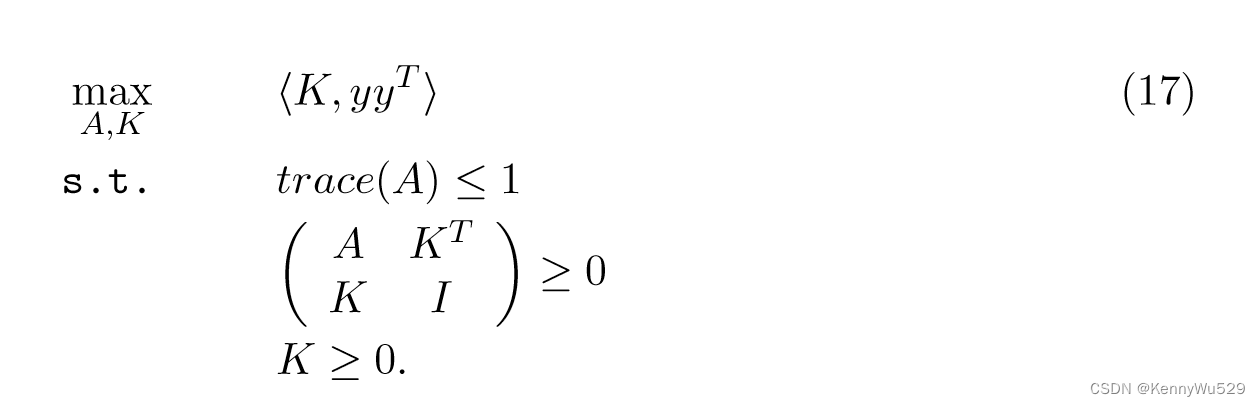
给定标记的训练集 Sn tr = {(x1, y1), · · · , (xn tr , yn tr )} 和未标记的测试集 Tn t {xn tr + 1, · · · , xn tr + n t}，形式上，我们考虑一个内核矩阵的形式为：

其中 Kij = 〈Φ(xi), Φ(xj)〉, i, j = 1, · · · , ntr, ntr + 1, ntr + nt 。

然后，目标是通过优化“训练数据块training data block” Ktr 上的成本函数来学习最佳混合块 the optimal mixed block Ktrt  和最佳“测试数据块 test data block” Kt。在约束 K = ΣMi−1 μiKi 的情况下，其中给定集合 K = {K1,···,KM } 且需要优化 μi，我们可以将式（17）中的 K 替换为 Ktr并获得用于学习核矩阵的SDP公式。

？？？这里是指在（17）中把K代为Ktr，求解SDP得到Ktr，再优化“训练数据块training data block” Ktr 上的损失函数（指的是6.1中的那俩吗？？）来学习最佳混合块 the optimal mixed block Ktrt  和最佳“测试数据块 test data block” Kt。？？？

“6.3 Quadratically Constrained Quadratic Program (QCQP)”  6.3 二次约束二次规划（QCQP）

Bach等人 (2004) 引入了一种称为支持核机 (SKM) 的新颖分类算法。

假设将 Rk 分解为 m 个块的乘积：Rk = Rk1 × · · · × Rkm，则每个数据 xi 可以分解为 m 个块分量，xi = {x1i, · · · , xmi}。类同（15）目的是找到一个线性分类器，y=sign(wTx+b)，在数学和计算机运算中，sign函数的功能是取某个数的符号（正或负）： 当x>0，sign (x)= 1；当x=0，sign (x)= 0；当x<0，sign (x)= -1 ，其中w=w1，····，wm 。

为了获得向量w的稀疏性并使w中的大部分分量为零，使用1-范数和2-范数对w进行惩罚。因此，原始问题可以表述如下：

该优化问题可以看作二阶锥规划（SOCP）问题，然后对偶问题由下式给出：

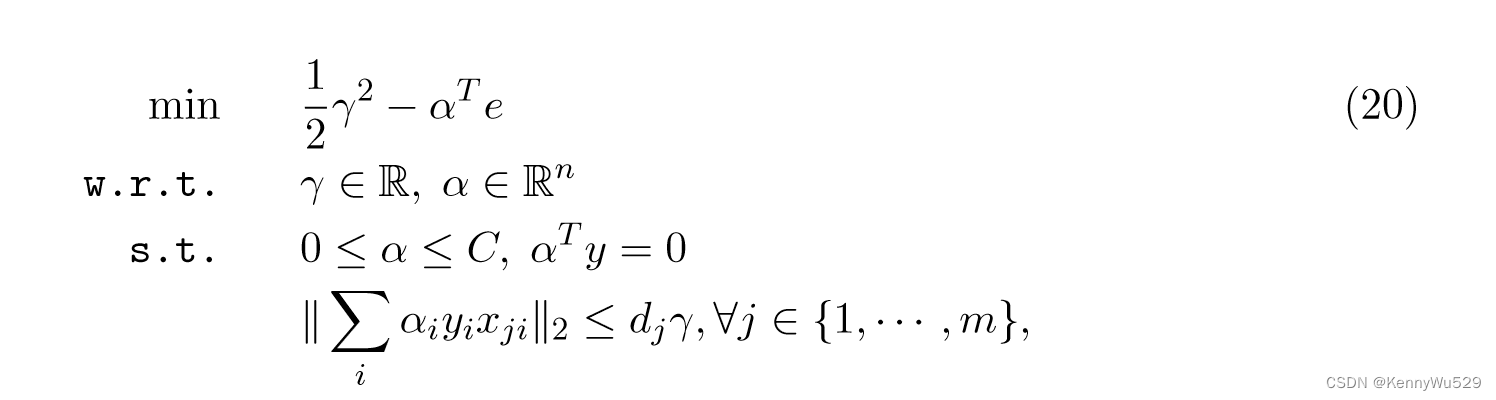
这与 Lanckriet 等人（2004）的 QCQP 公式完全相同。然而，这种 SOCP 公式的优点是 Bach 等人(2004) 为具有 Moreau-Yosida 正则化的 SKM 开发了一种 SMO 算法，并将原始问题转化为：

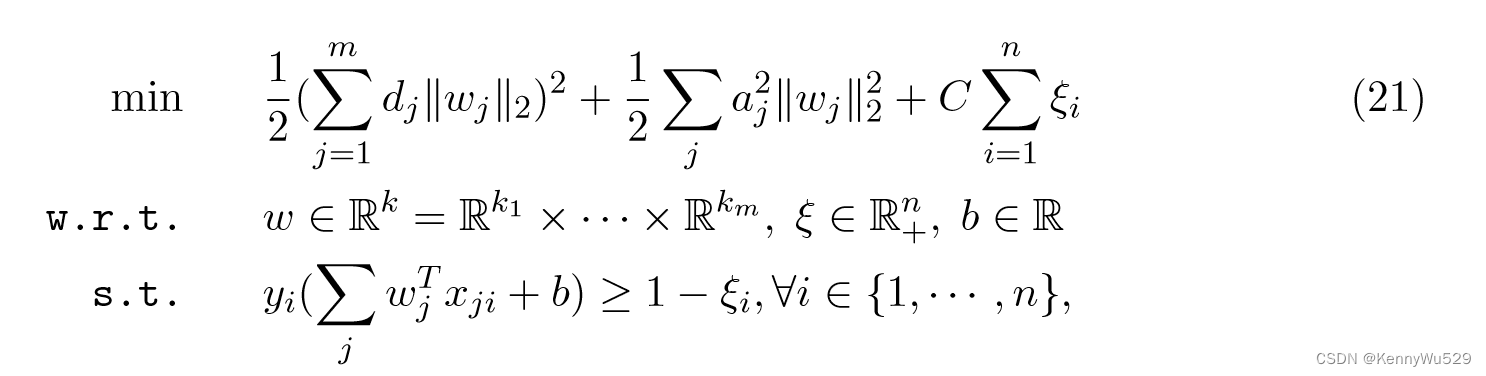
其中 {aj} 是 MY-正则化参数。

“6.4 Semi-infinite Linear Program (SILP)” 6.4 半无限线性规划（SILP）

索南伯格等人 (2006a,b) 遵循不同的方向，并将问题表述为半无限线性规划 (SILP)。从方程式(20) 开始等价的多核学习对偶修改为：

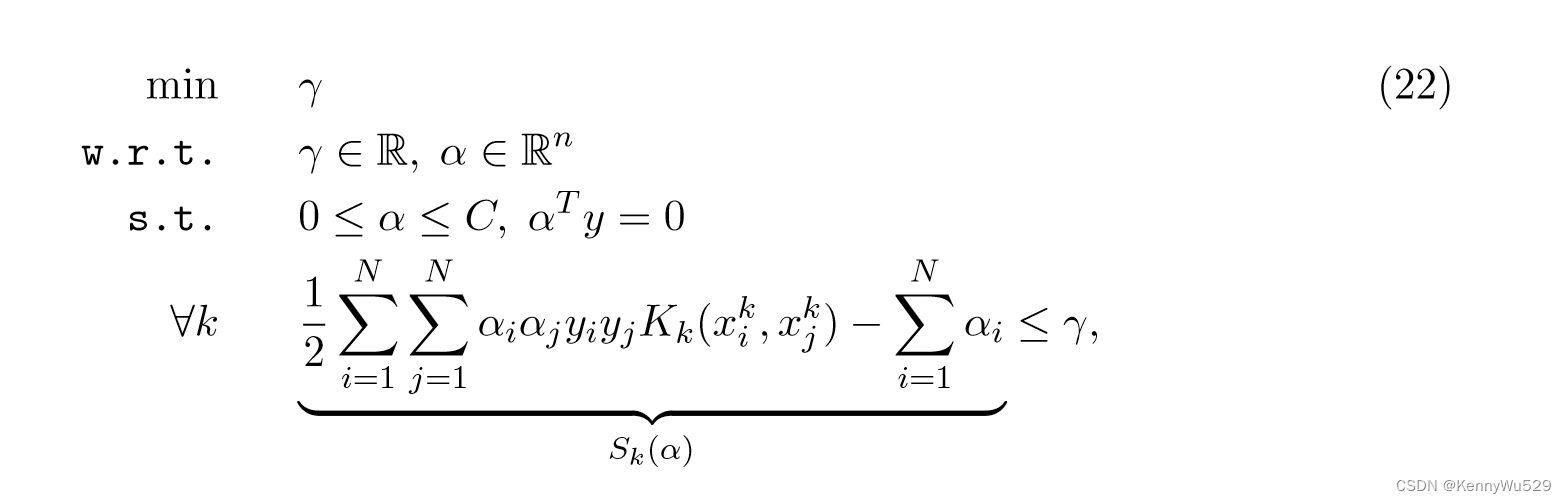
这可能可以通过以下方式解决

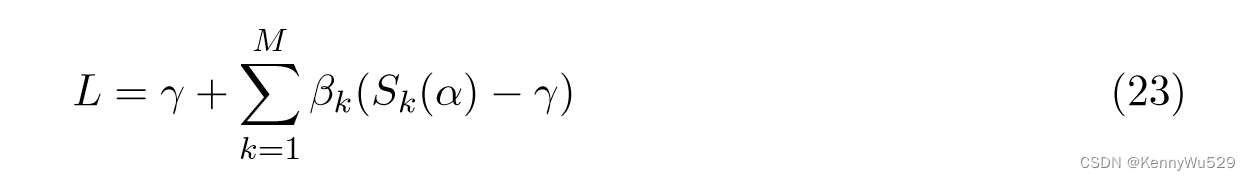
最小化 w.r.t α 和最大化 w.r.t β。对 γ 求导并为零，得到约束 Σ k βk = 1。等式(23) 可以简化为最小-最大问题

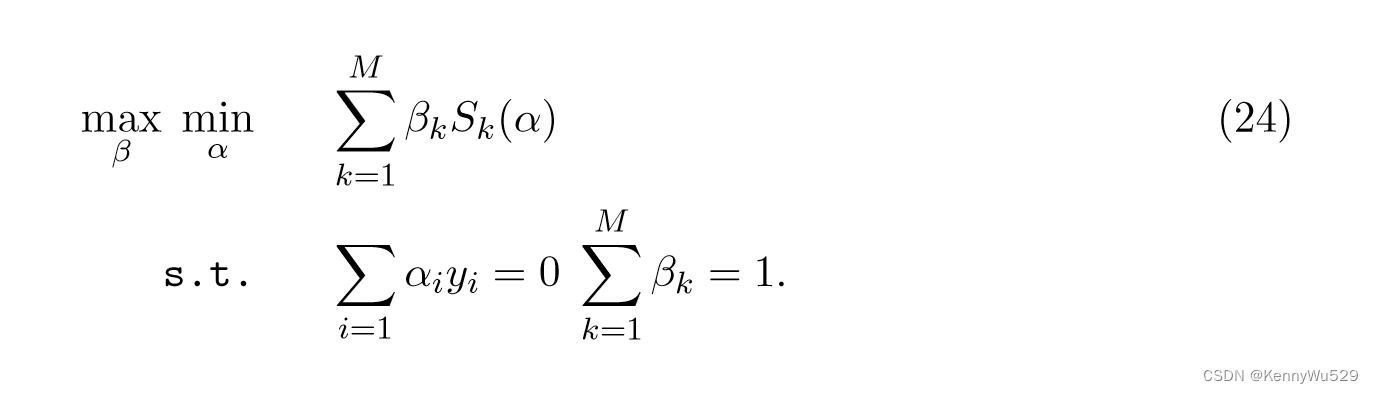
假设α*是最优解，并给出 θ=L=S(α*,β) 的定义，式(23) 等价于下面的 SILP 问题：

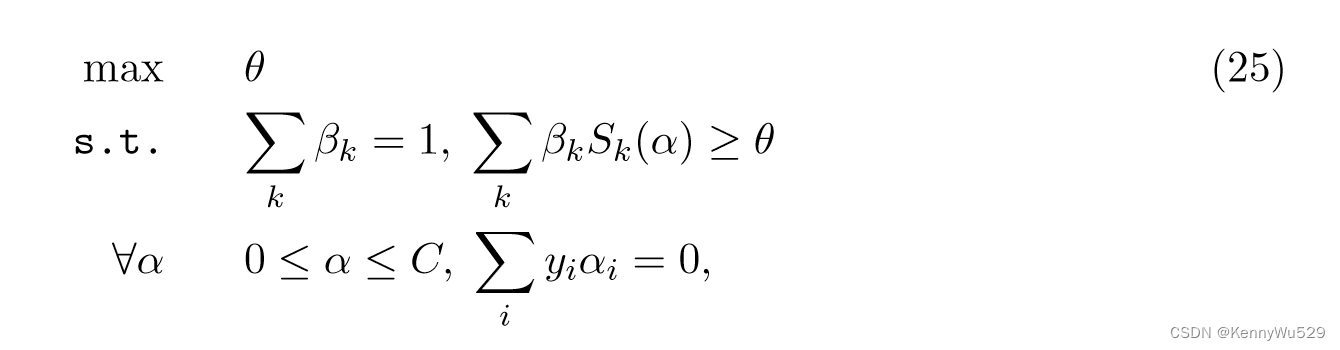
其中 θ 和 β 仅受到线性约束，但由于 α 的可能值，存在大量约束。

与 SDP 和 QCQP 相比，SILP 公式的计算复杂度较低，并且可以使用现成的 LP 求解器和标准 SVM 实现来有效解决该 SILP 问题。因此，它使我们能够有效地处理超过十万个示例或数百个内核。

“6.5 Simple MKL” 6.5 简单MKL

拉科托马蒙吉等人（2007，2008）背离了巴赫等人(2004) 提出的框架。 并通过自适应 2-范数正则化公式提出了多核学习的不同原始问题。受多重平滑样条框架（Wahba，1990）的启发，提出的原始公式是

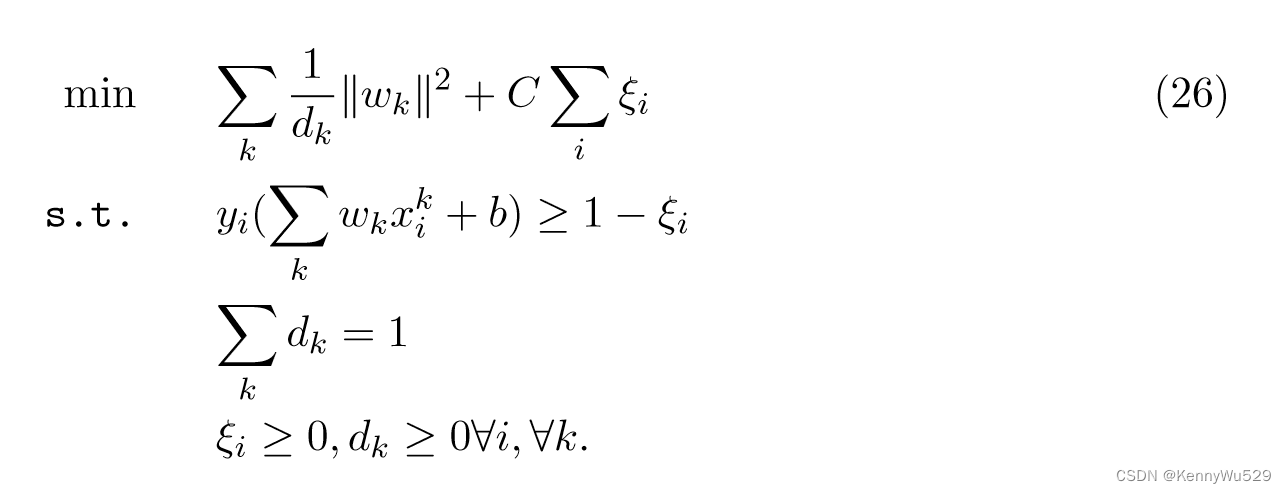
请注意，dk 控制核函数的平滑度，向量 d 上的 1-范数约束将导致具有少数基核的稀疏决策函数。

通过定义最优SVM目标值J(d)为

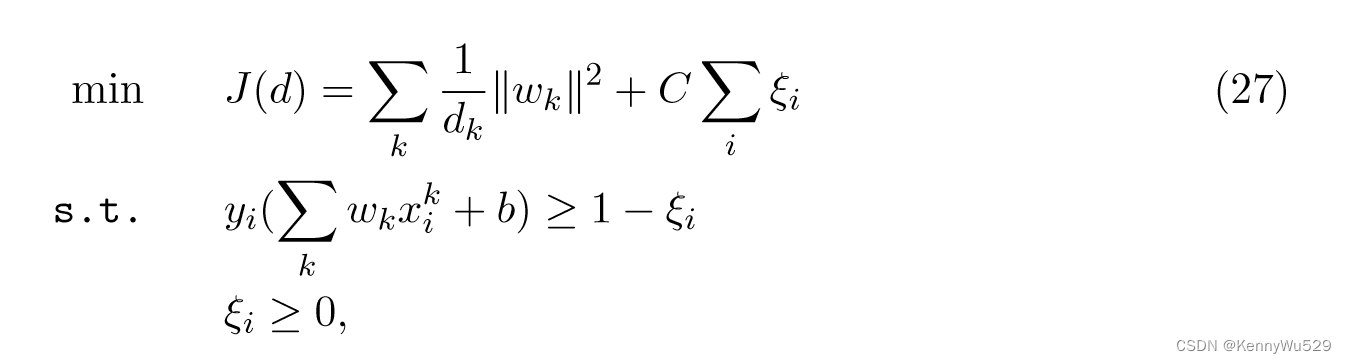
原始优化问题可以重新表述为

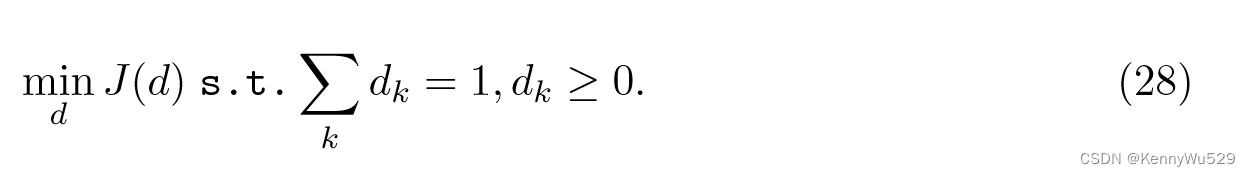
解决该问题的总体过程包括两个步骤：

首先，在给定 d 的情况下求解典型的 SVM 优化问题 J(d)；

其次，通过梯度下降更新 d，同时确保满足 d 的约束。

这种新颖的多核学习框架称为简单 MKL，它已被证明比 SILP 问题更有效。

Chapelle 和 Rakotomamonjy (2008) 研究了使用二阶优化方法来解决 MKL 问题，并提出 hessian MKL 作为简单 MKL 的扩展。在每次迭代中，第二步，hessian MKL 使用通过最小化 QP 问题找到的牛顿步来更新内核权重。结果表明，hessian MKL 在计算效率方面优于简单 MKL。

SILP 方法经常会遇到收敛速度慢的问题，因为它仅根据割平面模型更新核权重。简单的MKL是高效的；但是，它不使用先前迭代中计算的梯度，这些梯度对于提高搜索效率很有用。徐等人 (2009a) 扩展了the level method，并将其应用于多核学习，以克服 SILP (Sonnenburg et al., 2006b) 和简单 MKL (Rakotomamonjy et al., 2007) 的缺点。遵循 SILP 方法，该算法有一个额外的步骤，通过投影到水平集来调整从切割计划模型获得的核权重的解。这种调整确保新解接近当前解并减小目标函数。

“6.6 Group-LASSO Approaches”  6.6 群-LASSO方法

当内核可以划分为与输入或源的子集相对应的组时，考虑组合内核之间的组结构是合理的。在学习过程中，最好抑制与分类任务无关的核或组，否则将选择所有属于与任务相关的同一组的核。

基于这个想法，Szafranski 等人（2008，2010）开发了复合核学习（CKL）方法，该方法扩展多核学习问题到考虑核之间的组结构和构建与group-LASSO 的关系（Yuan 和 Lin，2006）。 Rakotomamonjy 等人的 MKL 公式 (2008) 被修改以获得以下的 CKL 公式：

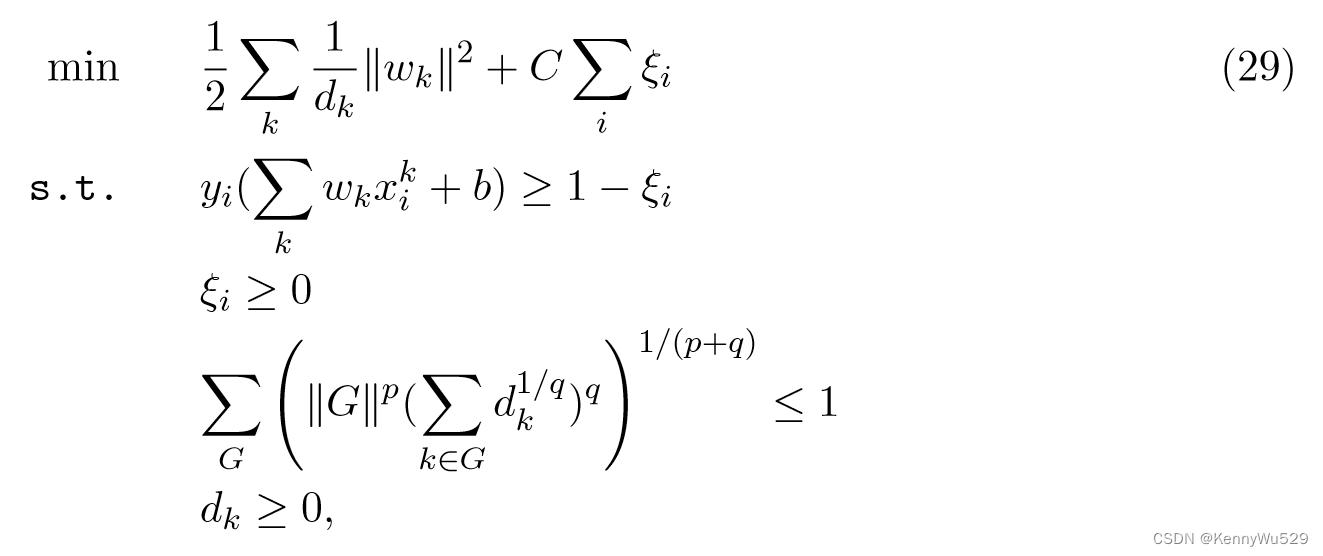
与MKL相比，目标函数多乘1/2，多了第三个约束

其中 p 和 q 根据当前问题设置，G 表示核的一个子集，‖G‖ 是组 G 的大小。

注意第三个约束：在 p = 0、q = 1 的特定情况下，第三个约束为ΣGΣk∈Gdk，对 RKHS 范数施加LASSO类型惩罚，当 p = 1、q = 0 时，第三个约束为ΣG||G||#{k∈G|dk≠0｝对 RKHS 范数施加 group-LASSO类型惩罚。

徐等人 (2010) 讨论了多核学习和 group-LASSO 正则化器之间的联系，并将 MKL 推广到 Lp-MKL，限制了 p 范数核权重。该算法为整个 Lp 模型系列提供了统一的解决方案，此外，可以通过封闭形式的公式计算核权重，而不依赖于其他商业软件。

Subrahmanya 和 Shin (2010) 提出了一种称为稀疏多核学习 (SMKL) 的算法，该算法通过在组上引入基于对数的惩罚，将组特征选择推广到核选择。与现有的多核学习框架相比，该方法可以从带有一个更稀疏的解的一个大量候选列表中自动选择最佳数量的源。

“6.7 Bounds for Learning Kernels” 6.7 学习核的界限

多核学习中检查的最常见的核系列是受trace条件约束的某些固定核的非负或凸组合，可以将其视为 L1 或 L2 正则化，或其他 p 值的 Lp 正则化。

兰克里特等人(2004) 表明，当从 k 个基核的凸组合中选择一个核时，学习分类器的估计误差受 O(√ k/γ2n ) 限制，其中 γ 是学习分类器在该核下的边际。该界限收敛，并且可以被视为该内核系列的第一个信息泛化界限；

然而，边际复杂度项 1/γ2 和基核数量 k 之间的乘法交互并不鼓励使用太多基核。它表明，即使学习几个内核参数也会导致所需样本量的成倍增加。

Srebro 和 Ben-David (2006) 提出了具有伪维度 dΦ 的核族的泛化界限。大多数内核族的伪维度与我们对一族维度的直观概念相似；特别是，k 个基核的线性或凸组合族的伪维度至多为 k。具有边际 γ 的 SVMs 的估计误差以 √[O(dΦ + 1/γ2)/n] 为界，这表明受所需样本量的限制，O(dΦ + 1/γ2) 仅随着允许的内核家族的增加而增长。

Ying 和 Campbell (2009) 表明，正则化核学习系统的泛化分析简化为对在候选核上的二阶 Rademacher 混沌过程上界的研究，并且他们使用了度量熵积分和候选核集合的伪维度来估计经验 Rademacher 混沌复杂度“empirical Rademacher chaos complexity” 。对于伪维度 k，如 k 个基核的凸组合的情况一样，它们的界限为 O(√k(R2/ρ2)(log(m)/m))，因此与 k 相乘。

基于对所考虑的假设集的 Rademacher 复杂度的组合分析，Cortes 等人 (2010) 提出了另一个具有 L1 约束的泛化边界，该约束仅对核数 k 具有对数依赖性。界限在 O( √(log k)R2/ρ2m ) 中，因此它对于大量内核有效，特别是对于 k ≫ m，并且它仅包含对内核数量的 √log k 依赖性，这是紧的并且相当有利。

假设不同核对应的不同视图不相关，Kloft 和 Blanchard (2011) 得出了 Lp 范数多核学习的局部 Rademacher 复杂度的上界。给定核数 M 和半径 D，中心相同独立内核的边界的量级为 O( √Σj∞ min (rM, D2M2/p*λj))。从上限来看，获得了比以前的方法更紧的超额风险界限，从而实现了 O(n−α/(1+α) ) 量级的快速收敛速度，其中 α 是各个内核的最小特征值衰减率。

“7. Subspace Learning-based Approaches” 7. 基于子空间学习的方法

基于子空间学习的方法旨在通过假设输入视图是从该子空间生成的来获得由多个视图共享的潜在子空间。除了众所周知的典型相关分析（CCA）之外，最近还出现了其他更有效的构建子空间的方法。

“7.1 Algorithms based on CCA”  7.1 基于CCA的算法

典型相关分析（CCA）是一种对两组（或多组）变量之间的关系进行建模的技术，它已在处理多视图数据的各种学习问题上取得了巨大成功。

“7.1.1 A review of CCA” 7.1.1 CCA 回顾

对于 X ∈ RD1×N 和 Y ∈ RD2×N ，CCA 计算两个投影向量 wx ∈ RD1 和 wy ∈ RD2，从而以下相关系数：

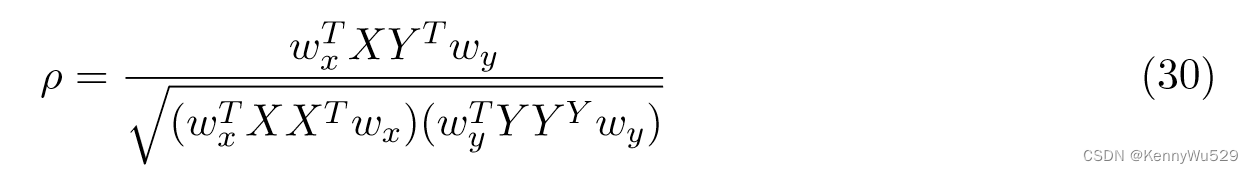
被最大化。由于 ρ 对于 wx 和 wy 的缩放是不变的，因此 CCA 可以等价地表述为

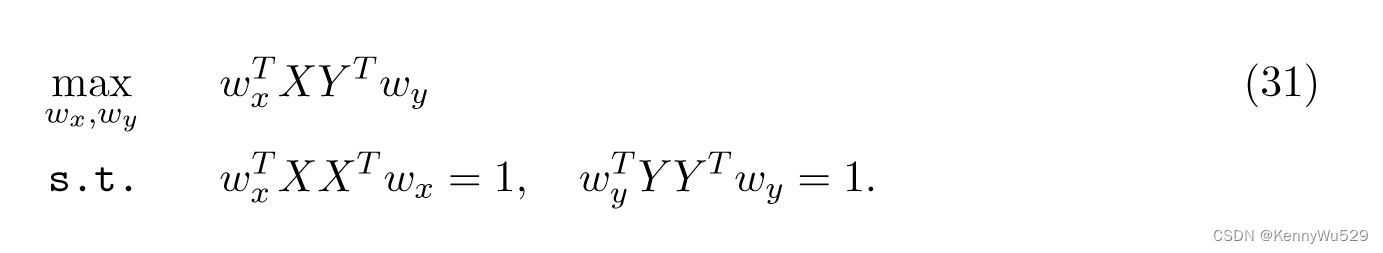
假设YYT是非奇异的，则wx可以通过求解以下优化问题得到：？？？(怎么推出的？？)

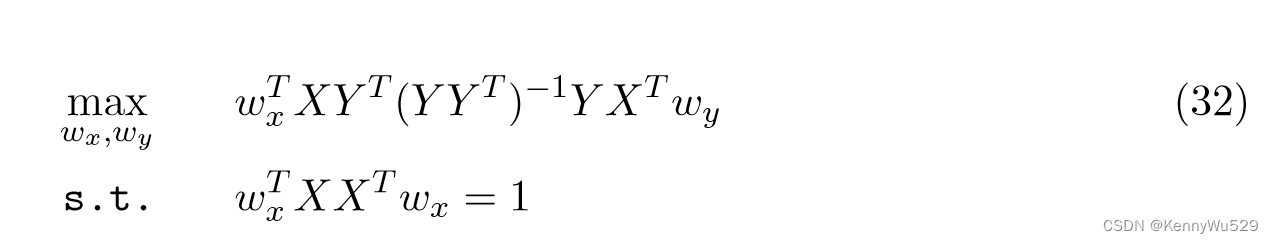
方程中的两种公式 (31) 和 (32) 尝试找到与以下广义特征值问题的最大特征值相对应的特征向量：

从（32）推（33）

L = f - λ/2(wxTXXTwx -1)

dL/dwx = XYT(YYT)-1YXTwy - λXXTwx = 0 ？？？   （33）中为wx

从（31）推（33）：

a=wx,b=wy,Σ11 = XXT,Σ12=XYT，Σ22 = YYT

由λ = θ，简化方程得：

把（2）代入（1），并令η = λ2，即得（33）

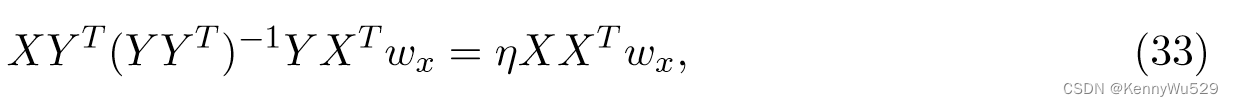
其中 η 是对应于特征向量 wx 的特征值。

“7.1.2 Kernel CCA” 7.1.2 内核CCA

典型相关分析（CCA）是一种线性特征提取算法，但对于许多表现出非线性的现实世界数据集，线性投影不可能捕获数据的属性。核方法提供了一种通过将数据映射到更高维空间然后在该空间中应用线性方法来处理非线性的方法。

正式给定一对数据集 X ∈ RD1×N 和 Y ∈ RD2×N ，CCA 寻求找到线性投影 wx ∈ RD1 和 wy ∈ RD2 ，使得在投影之后，两个数据集中的相应示例在投影空间中最大程度地相关。为了获得 CCA 的核公式，通过将投影方向表示为 wx = Xα 和 wy = Yβ 来进行对偶表示，其中 α 和 β 是大小为 N 的向量。在对偶公式中，X和Y之间的相关系数可以写为：

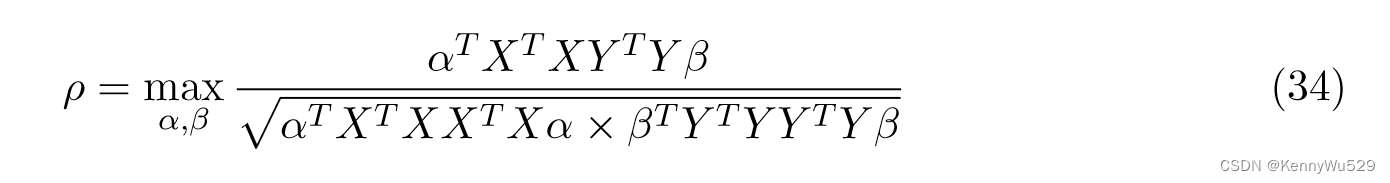
把 wx = Xα 和 wy = Yβ 代入（30）得到（34）

现在，利用 Kx = XTX 和 Ky = YTY 是 X 和 Y 的核矩阵这一事实，核 CCA 相当于解决以下问题：

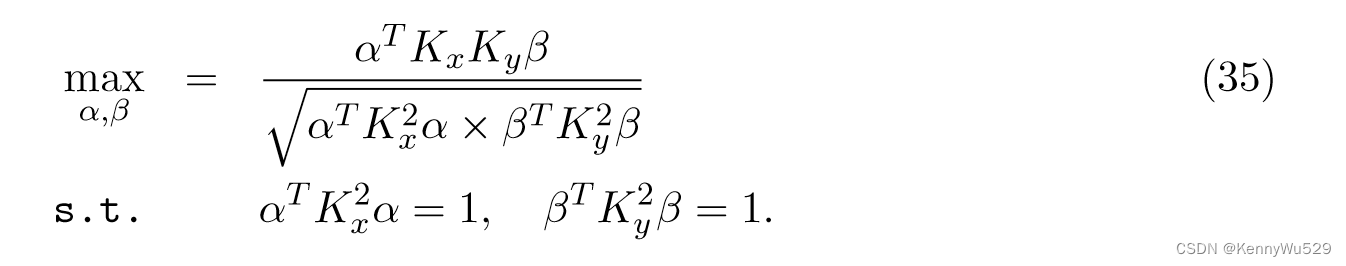
KCCA 通过在数据的两个视图 X 和 Y 中使用示例的核矩阵 Kx 和 Ky 来工作。与通过执行协方差矩阵特征分解来工作的线性 CCA 相比，KCCA 的特征值问题由下式给出：

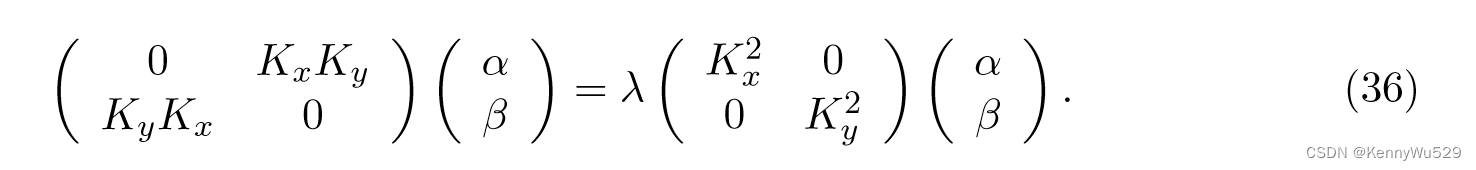
（35）--> (36): 类同前面（31）--> (33) 的推导，得到 λ = θ后，把俩偏导=0 的式子写成矩阵形式，即得（36）

在线性核的情况下，KCCA退化为标准CCA。

KCCA 可以隔离两个视图之间相关的特征空间方向，并且可能期望代表共同的相关信息；因此，实验表明 KCCA 可以成为提高支持向量机 (SVM) 等分类算法性能的有效预处理步骤。

Farquhar 等人 (2005)将 KCCA 与 SVM 组合成单一优化器，提出了一种称为 SVM-2K 的方法，它可以看作是两个不同 SVM 的全局优化，两个特征空间中各有一个 SVM。与 KCCA 表征的 2-范数略有不同，SVM-2K 使用松弛变量采用一个 ε-不敏感的 1-范数，来衡量不满足 ε 相似性的点的数量：

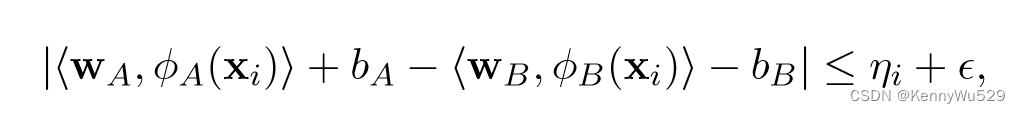
其中wA,bA和wB分别是第一个和第二个SVM的权重weight和偏差bias。然后对于通常的1范数支撑向量机SVM约束，目标问题可以写成：

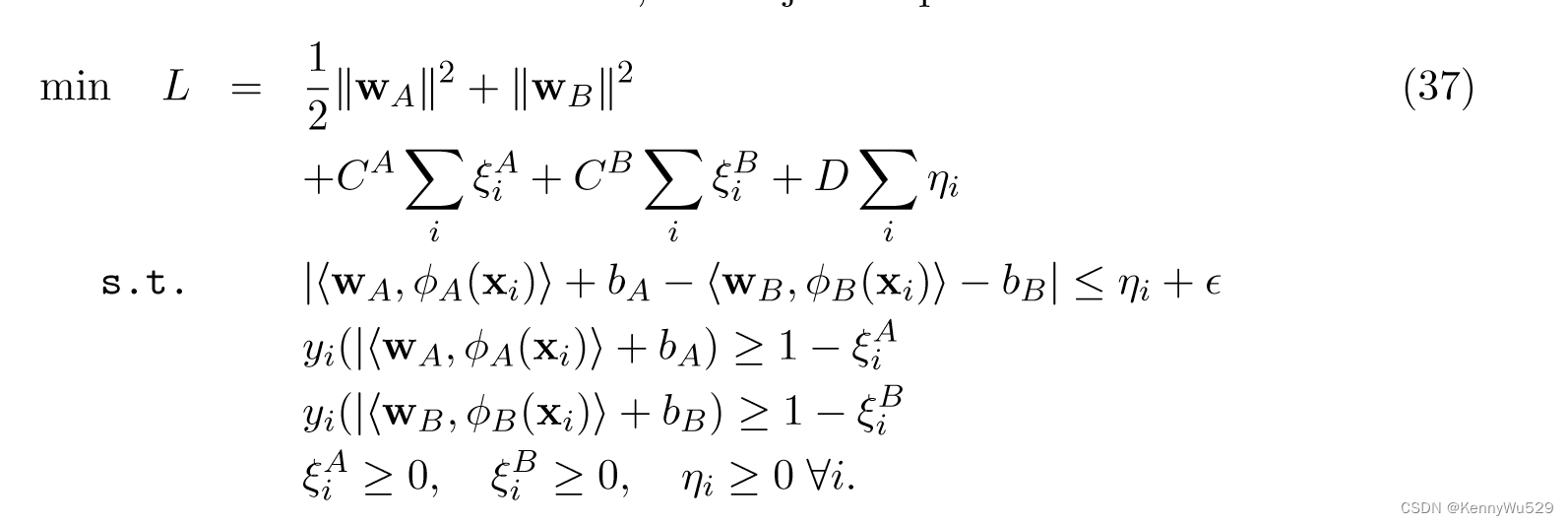
最终的决策函数为：

“7.1.3 Theoretical analysis of CCA” 7.1.3 CCA理论分析

典型相关分析 (CCA) 可以被视为寻找两组变量的基向量，使得这些基向量 xa = waT Φa(x) 和 yb = wbTΦb(y) 上的投影之间的相关性相互最大化。

KCCA 使用核技巧来生成 CCA 的非线性版本，通过寻找函数 f ∈ Hx 和 g ∈ Hy 使得随机变量 f (x) 和 g(y) 具有最大相关性。这导出了内核化形式 KCCA

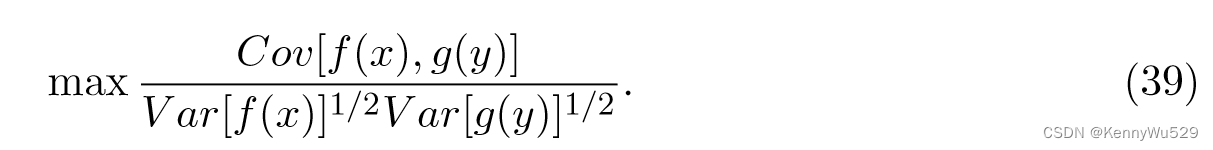
在实践中，我们必须从有限样本中估计所需的函数，则方程(39)的一个经验估计是

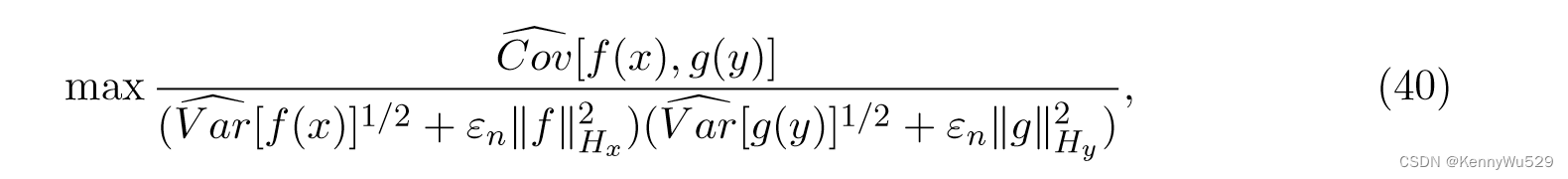
其中 εn 是正则化系数，n 是示例数。Fukumizu等人 (2007) 通过提供正则化参数的比率研究了建立 KCCA 一致性的一般问题，并证明了当

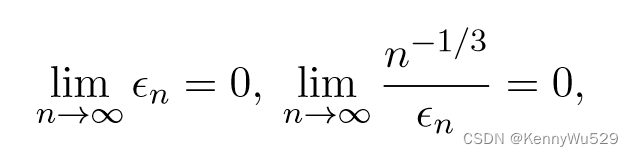
对于正则化系数εn的衰减，保证了核CCA的L2范数的收敛性。

Hardoon 和 Shawe-Taylor (2009) 使用回归公式提出了 KCCA 的有限样本统计分析。通过计算  ga,b(x, y) := ̂ E[‖WaTΦa(x)−WbTΦa(y)‖2]  的经验期望值，新数据的误差界限可以通过使用 Rademacher 复杂度来获得。形式上，给定由根据分布 D 绘制 i.i.d 的有界核 ka 和 kb 定义的特征空间中大小为 L 的配对训练集 S = {(xi, yi)}，则在概率大于 1 − δ 的 S生成过程中，新数据上ga,b(x, y) 的期望值的边界为

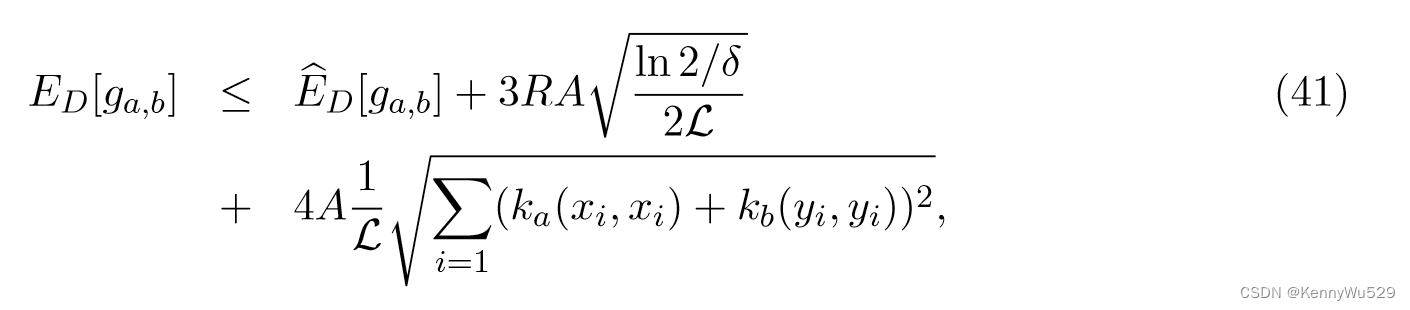
其中

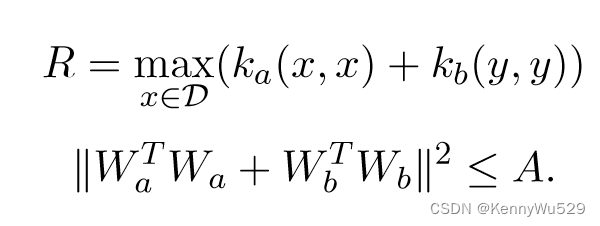
这表明了 KCCA 的正则化，因为它表明相关模式函数的泛化质量由权重向量范数的平方和控制。

Cai and Sun (2011)给出了核CCA的收敛速度分析。假设（Hx，Hy）分别是X和Y上函数的RKHS，VYX是从Hx到Hy的紧凑运算，并且存在算子Wl，Wr使得

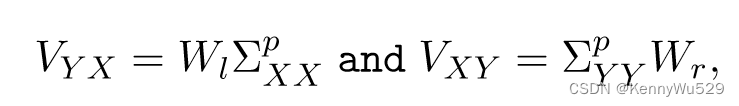
其中 ΣpXX 和 ΣpYY 是协方差算子。取 εn = ε1n−α 且 0 < α < 1/3，则概率至少为 1 − δ，我们有

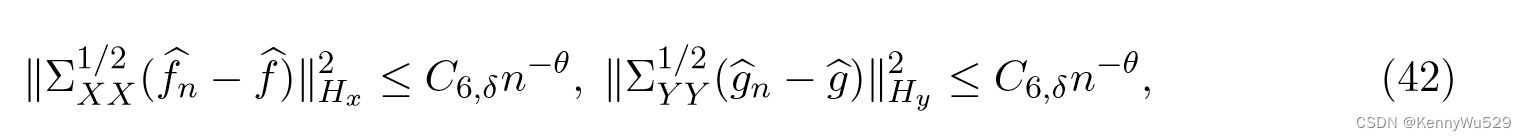其中 θ = min{1 − 3α, 2pα, α} 且 C6,δ 是与 n 无关的常数。所以当 0 < p ≤ 1 2 时，收敛速度为 min{1 − 3α, 2pα, α}。

“7.1.4 Related algorithms with CCA” 7.1.4 与CCA相关的算法

CCA作为进行多视图降维的通用工具已在不同领域得到广泛研究。最近，许多基于CCA的新算法被提出，以在不同的应用中扩展原始的CCA。

CCA 的一个流行用途是用于监督学习，其中一种视图源自数据，另一种视图源自类标签。在这种设置环境中，数据可以被投影到由标签信息引导的低维空间中（Yu et al., 2006）。然而，该算法实际上并没有使用数据的多个视图；它只是带有标签信息的单一视图方法。

Sharma等人(2012) 提出了广义多视图分析 (GMA)，它利用了最流行的监督和无监督特征提取技术是二次约束二次规划的特殊形式的解决方案这一事实。该算法可以被视为 CCA 的监督扩展，并且只要以分类或检索为目的并且标签信息可用，就有可能取代 CCA。

Chaudhuri 等人 (2009) 利用 CCA 将数据投影到由数据的均值为基组成的子空间，然后将标准聚类算法应用于该子空间。该子空间对于后续聚类很有价值，因为当投影到该子空间时，分布的均值分离良好，但来自相同分布的点之间的典型距离小于原始空间中的距离。传统的 CCA 和 KCCA 都假设所有视图的特征都可以用于示例，但对于许多多视图数据集来说，情况可能并非如此。

为了在此类数据集上应用多视图聚类，Anusua Trivedi（2010）利用拉普拉斯正则化的思想找到了一种处理不完整视图中数据缺乏的方法。给定K的已知部分，可以通过求解优化问题来找到核矩阵K的缺失部分；构建完整内核后，标准算法可以执行后续任务。

在半监督学习中，通常需要许多标记示例来训练初始的弱有用预测器，该预测器又用于利用未标记示例。通过 CCA 利用视图之间的相关性，Zhou 等人（2007）提出了一种仅用一个标记训练样本即可进行半监督学习的方法。在CCA的帮助下，可以测量原始未标记实例和原始标记实例之间的相似性。因此，可以分别选择具有最高和最低相似度的几个未标记示例作为额外的正例和负例。随着标记训练样本数量的增加，可以执行传统的半监督学习算法。

王等人 (2008) 结合 CCA 开发了一种新颖的多核学习算法。最初，输入数据由 m 个不同的内核映射到 m 个不同的特征空间，其中每个生成的特征空间被视为输入数据的一个视图。借用 CCA 的激励论点，即变换后的坐标中的 m 个视图可以最大程度地相关，可以提高分类器的泛化能力。

Zhu 等人(2012) 将 CCA 与 PCA 相结合提出了一种称为 MKCCA 的新方法来实现降维。 MKCCA 通过先执行 PCA 再执行 CCA 来改进内核 CCA，以更好地去除噪声并处理琐碎学习的问题。此外，通过将 CCA 与进行回归和分类的最小二乘法比较，Sun 等人 (2008) 将多标签分类中的 CCA 表述为最小二乘问题。

“7.2 Multi-view Fisher Discriminant Analysis” 7.2 多视图Fisher判别分析

与忽略标签信息的 CCA 不同，Dithe 等人(2008) 推广了费舍尔的判别分析，以在监督环境中找到多视图数据的信息预测。

“7.2.1 Two view Fisher Discriminant Analysis” 7.2.1 二视图Fisher判别分析

给定从同一底层语义对象的两个视图中提取的示例，分别表示为 Xa 和 Xb，二视图 Fisher 判别式选择两组权重 wa 和 wb 来解决以下优化问题

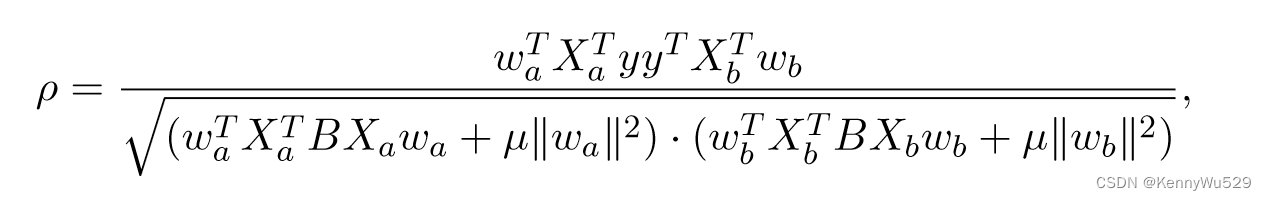其中 wa 和 wb 是每个视图的权重向量。由于方程不受 wa 或 wb 重新缩放的影响，因此优化可以受到以下约束

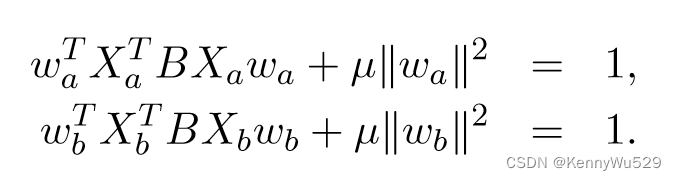
此优化的相应拉格朗日量可以写为

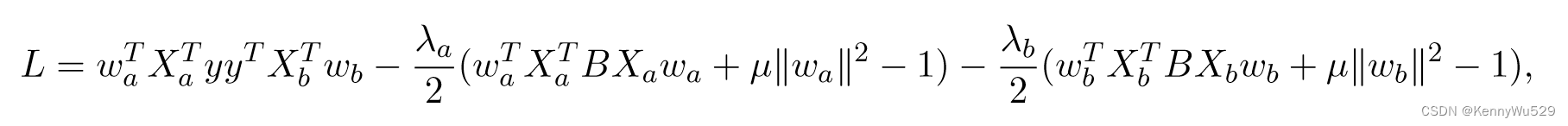
这可以通过对权重向量 wa 和 wb 求导来解决。

具体过程和7.1.1相同。

“7.2.2 Kernel two view Fisher Discriminant Analysis” 7.2.2 核二视图Fisher判别分析

通过引入两个对偶权重向量 wa = Xa T α 和 wb =Xb T β，我们有

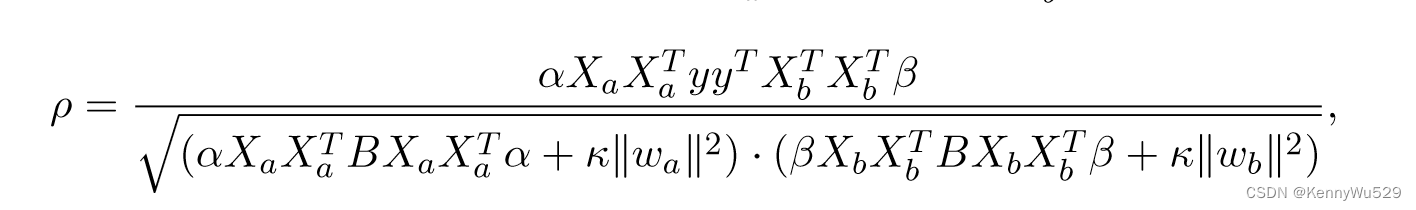
及其内核形式

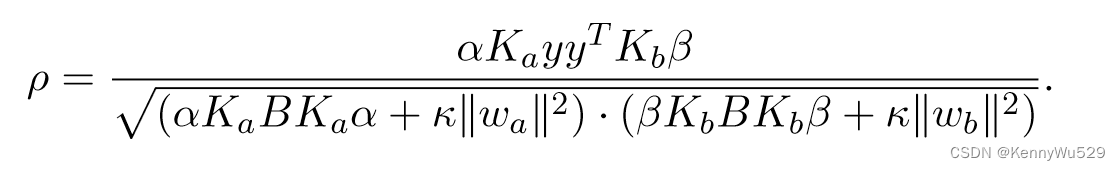
考虑到约束条件

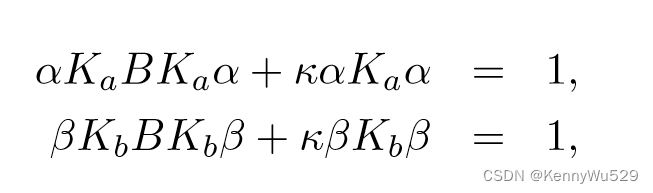
此优化的相应拉格朗日量可以写为

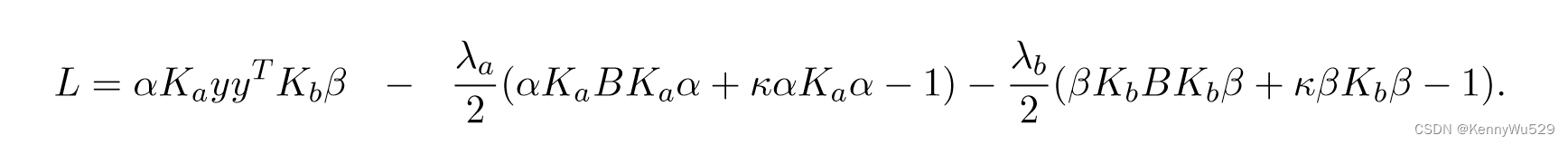对权向量α和β求导，即可解决上述问题。

具体过程和7.1.1相同。

“7.3 Multi-view Embedding” 7.3 多视图嵌入

由于高维数，即大量的输入特征，可能会导致估计的较大方差、噪声、过拟合，并且通常会导致学习器的复杂度较高和效率低下，因此有必要对这些特征进行降维并生成低维表示。然而，当面对多个特征时，考虑到它们之间的潜在联系，对每个特征执行降维并不是理想的解决方案。因此，可能需要采用先进的方法来同时对多个特征进行嵌入，并输出所有特征共享的有意义的低维嵌入。

现有的光谱嵌入算法假设样本是从向量空间中提取的，因此无法直接处理多视图数据。

夏等人（2010）开发了一种新的光谱嵌入算法，即多视图光谱嵌入（MSE），它对多视图特征进行编码以实现物理上有意义的嵌入。基于他们之前的补丁对齐工作（Zhang et al., 2009），MSE 可以描述如下。

MSE首先在一个视图上为一个样本构建一个补丁，然后给定来自不同视图的补丁，执行部分优化以获得每个视图的最佳低维嵌入。

然后，来自不同补丁的所有低维嵌入通过全局坐标对齐统一为一个整体。更正式地，给定第 i 个视图 Xi = [xi1, · · · , xin]，考虑任意点 xij 及其 k 个最近邻点，xij 定义为 Xij = [xij , xij1, · · · , xijk] 。对于 Xij ，我们想要找到一个局部映射 fij ：Xij  → Yij  ，其中 Yij  = [yij , yij1, · · · ,yijk]。第 i 个视图上第 j 个补丁的局部优化定义为

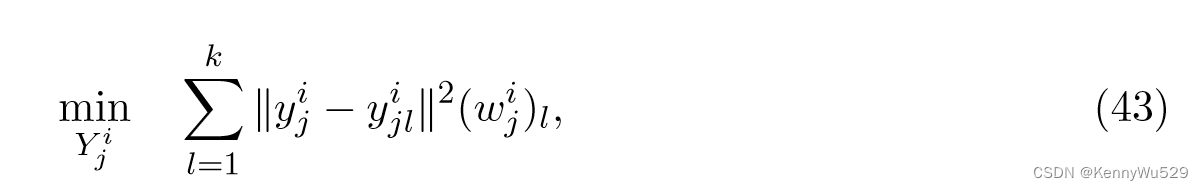
其中 (wij)l = exp(−‖xij − xijl ‖2/t)。等式 (43) 可以重新表述为

其中 tr(·) 是迹算子，Lij 对第 i 个视图上第 j 个补丁的目标函数进行编码。为了探索多视图的互补性，对部分优化施加一组非负权重α=[α1,···,αm]，因此第j个补丁的多视图局部优化为

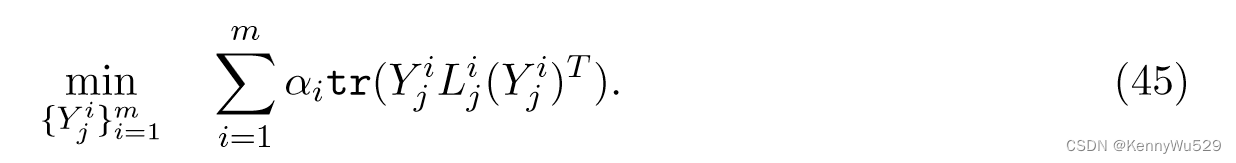
为了确保不同视图中的低维嵌入彼此全局一致，假设Yij  = [yij , yij1, · · · ,yijk]的坐标是从全局坐标 Y = [y1, · · · , yn]中选择的，则得到 Yij  = Y Sij ，其中 Sij 是用于对原始高维空间中的补丁中的样本关系进行编码的选择矩阵。通过总结所有局部优化，全局坐标对齐可以写为

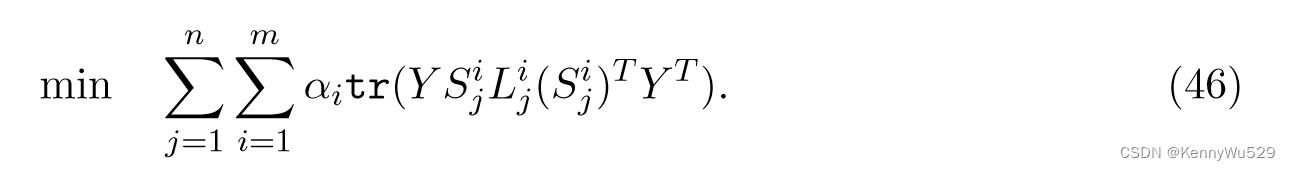
从方程(mse8)，第 i 个视图的对齐矩阵可以写为

为了确保每个视图对最终的低维嵌入做出特定的贡献，并考虑对变量的一些约束，最终的目标函数定义为

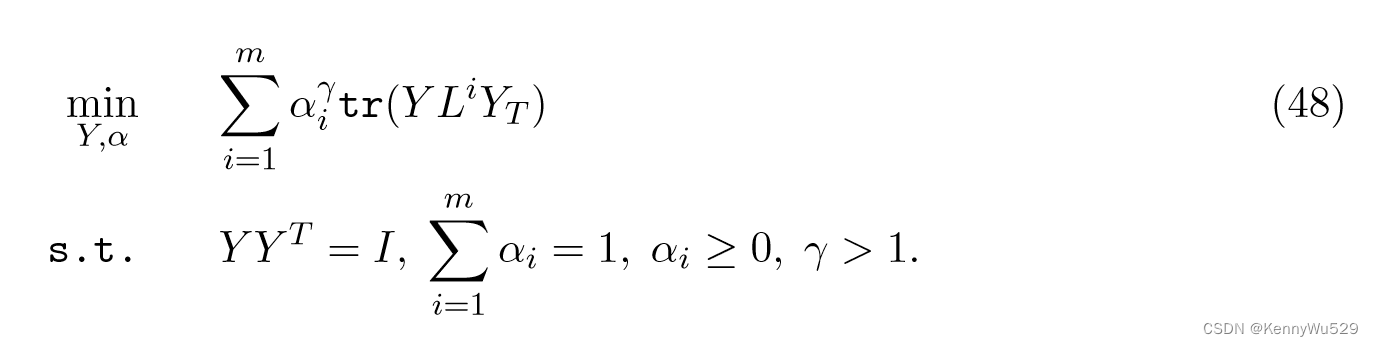
最后，MSE 可以通过同时保留每个视图的局部性来生成足够平滑的低维嵌入。

随机邻域嵌入（SNE）的主要思想是从成对距离 pair-wise distance 构建概率分布，其中较大的距离对应较小的概率，反之亦然。形式上，假设我们有高维数据点 {xi}ni=1，样本对上的联合概率分布可以用对称矩阵 P ∈ Rn×n 表示，其中 pii = 0 且 Σ i,j pij = 1。设yi为xi对应的低维数据，则低维嵌入embedding 中的概率分布Q定义为

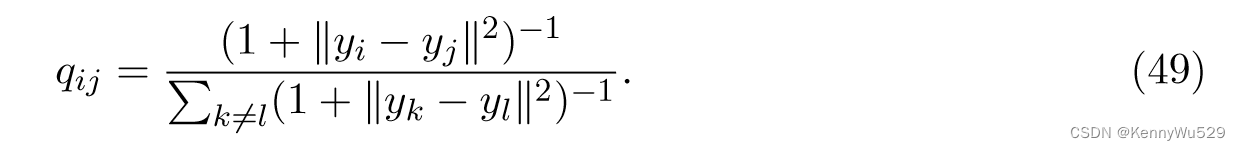
这种嵌入可以通过最小化两个概率分布的 KL 散度来获得

 

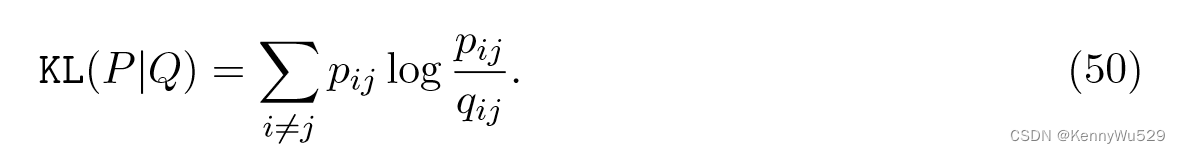
谢等人 (2011) 提出了 m-SNE 算法，通过向每个视图引入一个组合系数来推广 SNE 来处理多视图数据。最终高维空间上的概率分布为

其中 αt 是视图 t 的组合系数，ptij 是视图 t 上的概率分布。该组合系数在利用多视图数据中的互补信息和抑制噪声上起着重要作用。另外，原始目标函数仅包含KL散度；添加 2-范数正则化项来平衡所有视图的系数

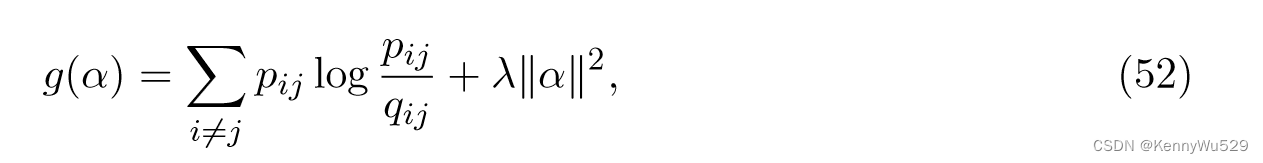
其中 λ 是权衡系数。

韩等人 (2012)提出了一种新的多视图数据稀疏无监督降维框架。

考虑到每个视图的特定统计属性，该算法首先使用主成分分析（PCA）算法从这些视图中学习低维模式。将学习到的每个视图的低维模式组合成一个统一模式后，低维共识表示的构造可以通过低维共识基础矩阵和一个加载矩阵来近似模式矩阵。

为了为多个视图的光谱嵌入选择最具辨别力的特征，将 1-范数添加到加载矩阵的列中，并对基础矩阵施加正交约束。随后开发了一种称为光谱稀疏多视图嵌入“Spectral Sparse Multi-View Embedding” （SSMVE）的新方法来有效地获得解。

此外，由于加载矩阵的每一行都是由几个部分连接而成的向量，这些部分对应于从不同视图学习到的不同模式，因此对加载矩阵的行施加了一种新颖的结构化稀疏诱导范数惩罚，以获得跨视图的子集的共享信息的灵活度。因此，提出了另一种具有结构化稀疏性惩罚的多视图降维方法，即结构化稀疏多视图降维“Structured Sparse Multi-View Dimensionality reduction” （SSMVD）。

“7.4 Multi-view Metric Learning” 7.4 多视图度量学习

多视图数据的度量学习的目标是将不同表示的数据构建到共享特征空间的嵌入投影，使得该空间中的欧几里得距离不仅在单个视图内有意义，而且在不同视图之间也有意义。

受跨媒体检索任务的推动，Quadrianto 和 Lampert (2011) 研究了度量学习问题，以找到允许最近邻查询的联合欧几里得距离函数。遵循以下经典原则：如果相关，则将样本拉到一起；如果不相关，则将样本分开，多视图度量学习的公式如下。

假设有两组 m 个数据点，X = {x1, · · ·, xm} 和 Y = {y1, · · ·, ym} 从两个不同的视图描述相同的对象，并且对于每个 xi ∈ X 存在来自 Y 的与 xi 相似的数据点的集合 Sxi。给定 X = Rd1 和 Y = Rd2，我们求投影函数

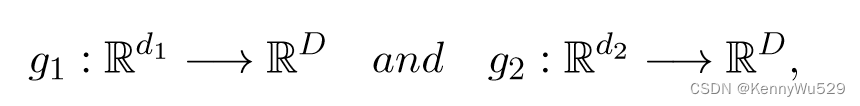
其中 D ≪ min(d1, d2) 尊重邻域关系 {Sxi }mi=1。考虑函数 g1(xi) = 〈w1, Φ(xi)〉 和 g2(yi) = 〈w2, Φ(yi)〉 的线性参数化，则度量 w1 和 w2 是学习的目标，并且目标函数可以写为

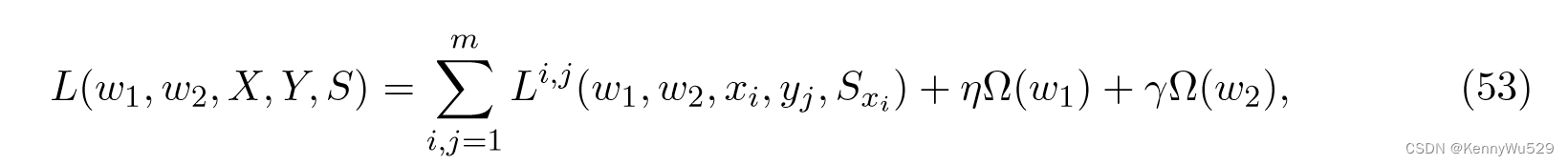
其中 Li,j(·) 是损失函数，Ω(·) 是参数的正则化器，η 和 γ 是权衡变量。

通过适当选择损失函数，可以表达投影数据预期具有的属性。特别是，如果希望确保不同视图中的相似对象被映射到附近的点，而不同视图中的不同对象将被分开，则损失函数可以设计为两个不同部分的并集

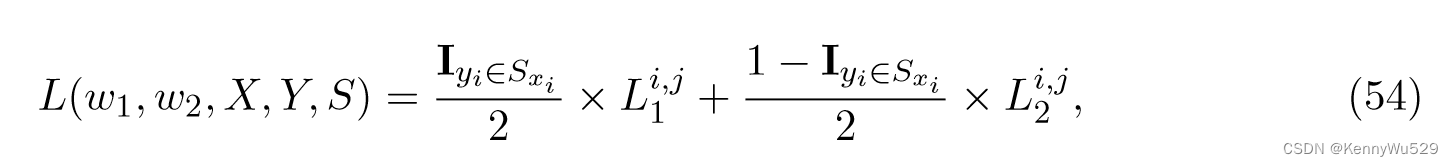
其中相似项 L1i,j 迫使相似的对象位于潜在空间中的邻近位置，而不同项 L2i,j 将不同的对象推离彼此。该目标函数可以分解为两个凹函数的差，因此可以通过凹凸过程（CCCP）有效地求解。

由于图像处理中可以提取各种不同的低级视觉特征来综合表示图像，因此很难选择依靠哪种特征来衡量图像之间的相似性。因此，Yu 等人(2012b)提出了一种半监督多视图距离度量学习（SSM-DML）算法来构建精确的度量来精确测量与多个视图相关的不同示例之间的差异。形式上定义一个矩阵 F = [F1T , · · · , FNT ]T ，其中 Fij 是带有标签 yj 的 xi 的置信度，然后可以通过最小化以下目标函数来获得该矩阵 F：

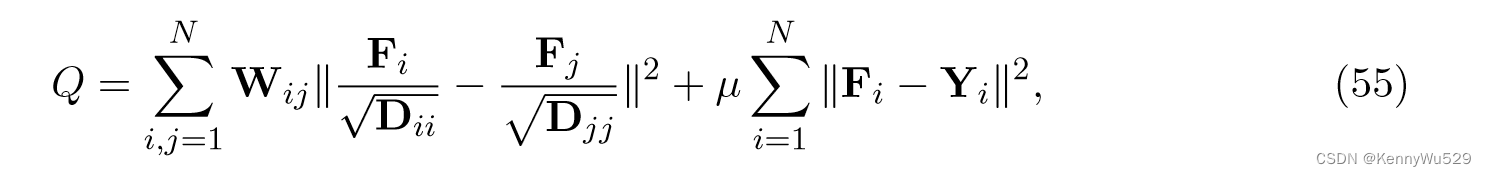
其中 W 是亲和矩阵，Wij 表示 xi 和 xj 之间的相异性度量，D 是对角矩阵，Dii 等于 W 第 i 行的总和。 方程(55)的第一项表示图上标签的平滑度，第二项表示训练数据的约束。假设 Xi 代表示例的第 i 个视图；

通过权重 α 线性组合由多视图特征集构建的图，方程 (55) 可以扩展到多视图特征集

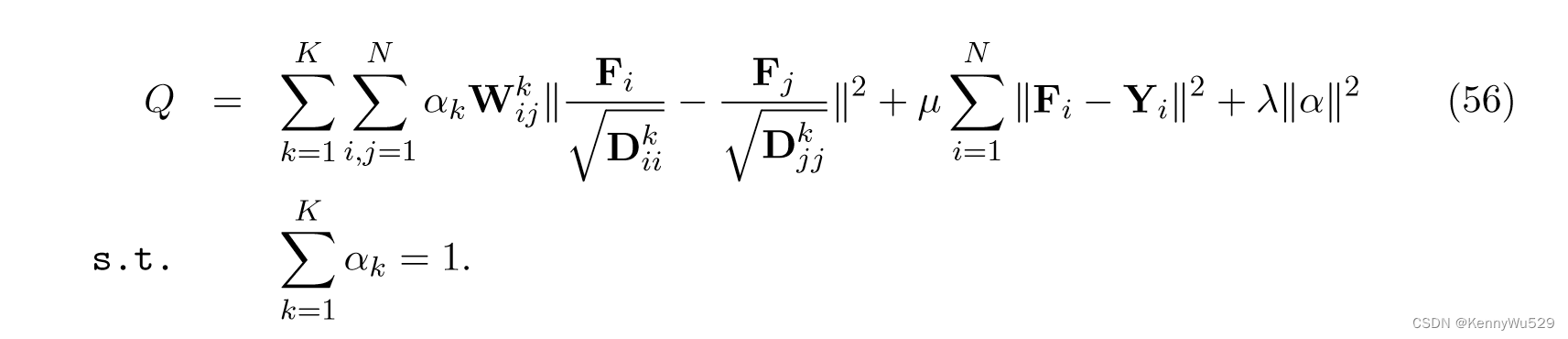
然后通过采用交替优化来解决上述优化问题，SSM-DML可以同时从多个特征集和未标记数据的标签中学习多视图距离度量。

翟等人 (2012)还研究了半监督学习环境中的多视图度量学习问题，提出了一种新方法，称为具有全局一致性和局部平滑性的多视图度量学习（MVML-GL），该方法共同考虑全局一致性和局部平滑性。

该算法分两步完成：

（1）寻找一个共享的潜在特征空间，建立来自关于标记实例的多视图观察空间的数据之间的关系；

（2）学习每个观察的输入空间与未标记和测试数据的共享潜在空间之间的关系。

值得注意的是，第一步是全局一致的，因为它同时考虑了每个视图中包含的几何结构以及不同视图数据之间的连接，而第二步是局部平滑的，这使得每个实例都有自己的特定距离指标而不是对所有实例应用统一的指标。此外，这两个步骤都可以表示为具有封闭形式解的凸优化问题，因此可以有效地解决它们。

“7.5 Latent Space Models” 7.5 潜在空间模型

除了上述旨在对多视图数据进行有意义的降维的方法外，还有专注于分析不同视图之间关系的工作。这些方法用于构建潜在空间模型，多个视图可以通过潜在变量相互连接，并且信息可以从一个视图传播到另一个视图。

“7.5.1 Shared Gaussian Process Latent Variable Model”  7.5.1 共享高斯过程潜变量模型

高斯过程 (GP) 是用于分类和回归的强大模型，它包含众多类别的函数逼近器，例如单隐藏层神经网络和 RBF 网络。 Lawrence (2004) 首先提出高斯过程潜变量模型（GPLVM）作为非线性降维的新技术。肖恩等人 (2006) 提出了共享 GPLVM (SGPLVM) 作为 GPLVM 模型的泛化，它可以处理多个观察空间，其中每组观察都由一组不同的内核参数进行参数化。

令 Y , Z 分别为从维度 DY , DZ 的空间绘制的观测值矩阵，X 为维度 DX << DY , DZ 的潜在空间。假设每个潜在点 xi 通过 GPs 参数化非线性函数 fY : X → Y 和 fZ : X → Z 生成一对观测值 yi, zi。通过使用指数 (RBF) 核来定义两个数据点 x,x’ 之间的相似度

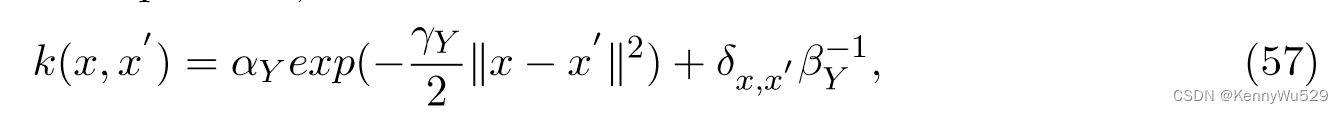
Y、Z 观测空间的先验 P (θY )、P (θZ )、P (θX ) (θ = {α, β, γ}) 和似然 P (Y )、P (Z) 由下式给出

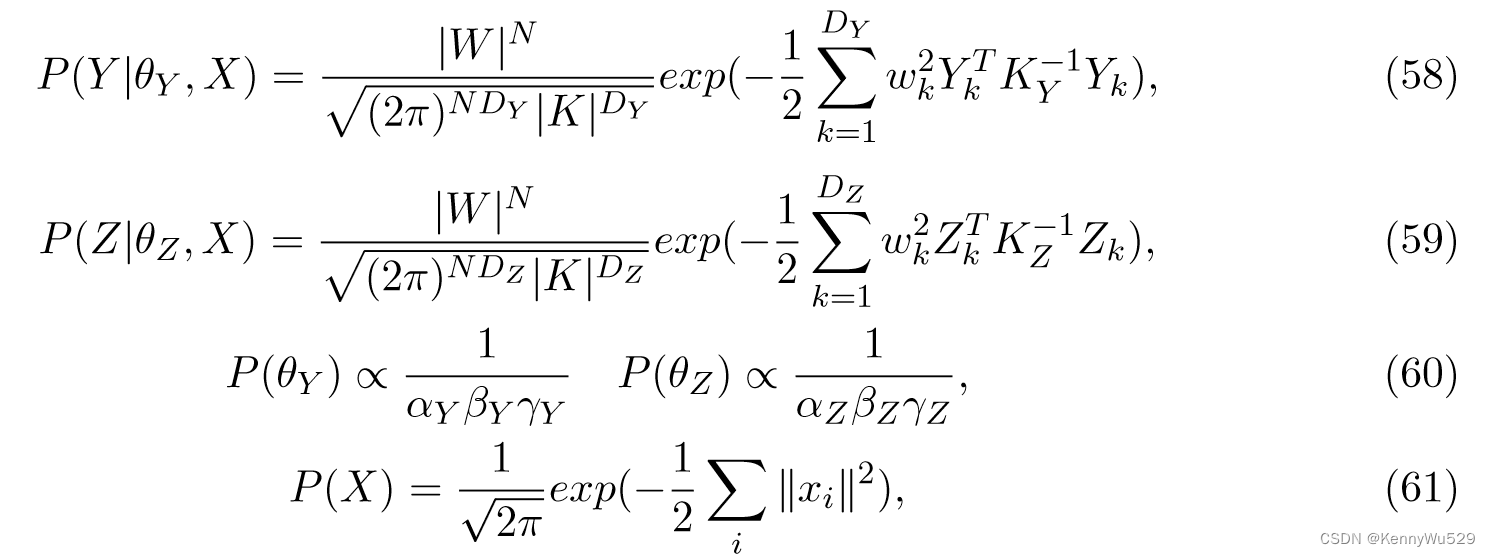
那么联合似然可以写为

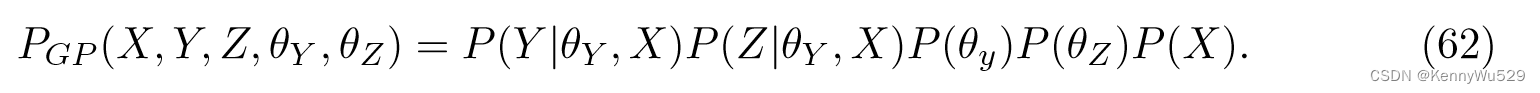
通过使用共轭梯度求解器来最大化方程(62)，该模型可以为每个观察空间学习一个单独的内核和一组公共潜在点。

给定一个经过训练的 SGPLVM，我们希望根据另一个观察空间中的参数来推断另一个观察空间中的参数。这个问题可以分两步解决。

首先，给定观测值 y ，我们使用 maxx Lx(x, y) 确定的最可能的潜在坐标 x。

一旦针对给定 y 推断出正确的潜在坐标 x，该模型就会使用经过训练的 SGPLVM 来预测相应的观测值 z。

“7.5.2 Shared Kernel Information Embedding” 7.5.2 共享内核信息嵌入

给定从分布 p(x) 中抽取的样本，内核信息嵌入KIE“Kernel Information Embedding” （Memisevic，2006）旨在找到一个低维潜在分布 p(z)，它捕获数据的结构，以及潜在空间和数据空间之间的显式双向概率映射。特别是，KIE 找到最大化潜在分布和数据分布之间的互信息的联合分布 p(x, z)：

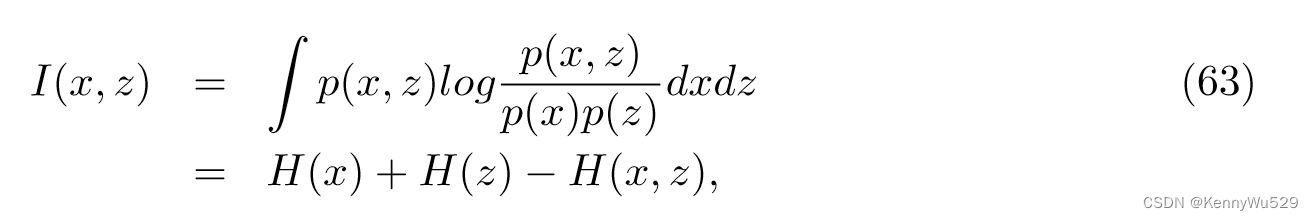
其中H(·)是通常的香农熵，可以通过核密度来估计。

共享 KIE (sKIE)(Sigal et al., 2009; Memisevic et al., 2012) 可以看作是 KIE 的扩展，通过最大化互信息 I((x, y) , z) 来构造两个视图的联合嵌入。假设给定 z 时 x 和 y 条件独立，I((x, y), z) 可以表示为两个互信息项之和，

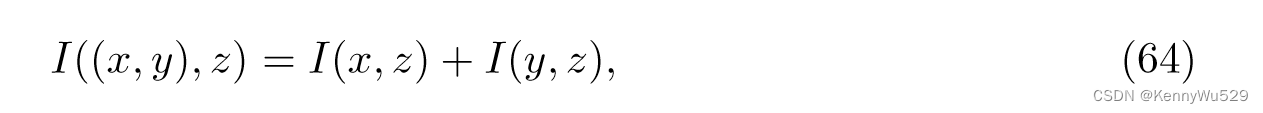
其中 I(x, z) 和 I(y, z) 可以表示为 KIE。

该算法的一个应用是人体姿势推断。对于判别姿势推断，目的是找到以输入图像特征 x* 为条件的可能姿势 y。那么条件姿态分布为：

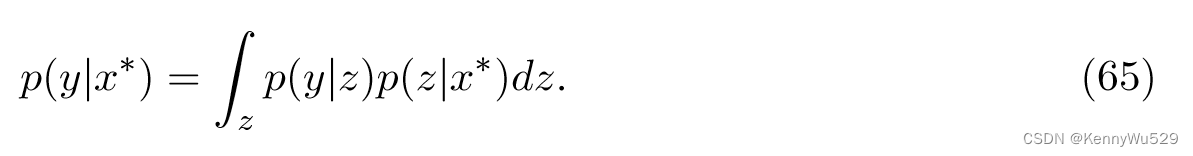
或者，重点可以放在识别 p(y|x*) 的主要模式上。为此，假设 p(y|x*) 的主模与条件潜在分布 p(z|x*) 的主模一致。也就是说，首先搜索 p(z|x*) 的局部最大值，K 个模式就表示为 {z* k}Kk=1 。从这些潜在点可以直接执行 MAP 推断或对条件姿态分布 p(y|z* k ) 进行期望。

“7.5.3 Factorized Orthogonal Latent Space” 7.5.3 分解正交潜在空间

sGPLVM和sKIE都只考虑数据视图中的共享信息，而忽略每个视图中的私有部分。萨尔兹曼等人(2010) 提出了一种名为 FOLS 的鲁棒方法，通过引入正交性约束将潜在空间分解为共享空间和私有空间，从而惩罚冗余的潜在表示。

对于最小分解，共享和私有潜在空间需要是非冗余的；换句话说，最好惩罚不同私人空间的冗余，从而鼓励在共享空间中表达公共信息。更正式地，将 Y i = [yi1, · · · , yiN ]T 定义为来自单个视图 i 的观测值集合，其中 1 ≤ i ≤ V 。另外，令 X = [x1, · · · , xN ]T 为不同视图之间共享的潜在空间，Z i = [zi1, · · · , ziN ]T  为第 i 个视图的私有空间，M i =  [mi1, · · · , miN ]T  是每个视图的联合共享-私有潜在空间，其中 mij = [xj, zij]。通过施加上述非冗余约束作为软惩罚，一个FOLS模型可以通过最小化

正交 + 低秩 + 能量守恒（节能）

其中 si 是 Mi 的奇异值，Ei 0 是流 i 的能量energy，L 是引入分解约束的特定模型的损失函数。在sGPLVM和sKIE模型中，L表示平方损失，或者每个联合潜在空间与其对应的数据流之间的负互信息。

“7.5.4 Factorized Latent Spaces with Structured Sparsity” 7.5.4 具有结构化稀疏性的因式分解潜在空间

受到稀疏编码技术的启发，Jia 等人（2010）提出了一种寻找潜在空间的新方法，其中信息被正确地分解为共享部分和私有部分，同时避免了先前技术的计算负担。特别是，该算法将每个视图表示为依赖于视图的字典条目的线性组合。虽然字典特定于每个视图，但这些字典的权重充当潜在变量，并且对于所有视图都是相同的。

更正式地说，为了找到表示多个输入模态的潜在嵌入 α 的共享-私有分解，该算法采用结构化稀疏性的思想，旨在找到一组字典 D = {D1, · · ·, DV }。这个问题可以表述为，

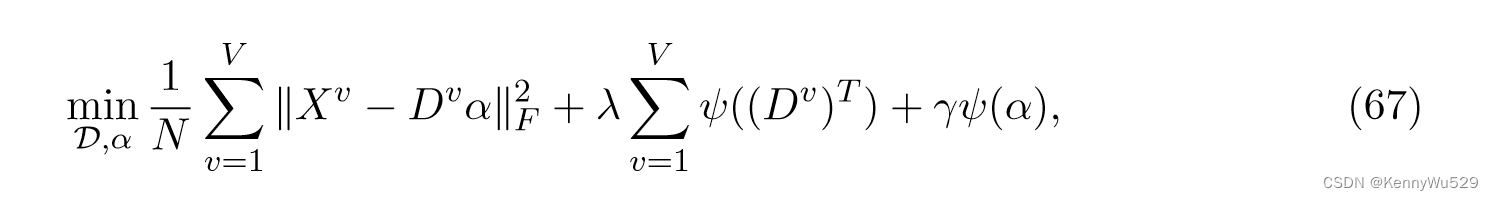
其中第一项衡量损失，第二项鼓励每个视图仅使用有限数量的潜在维度，第三项表示放宽秩约束以发现潜在空间的维度。

推理时，给定一个新的观测值{x1*,···,xV*}，可以通过求解以下凸问题得到相应的潜在嵌入α*

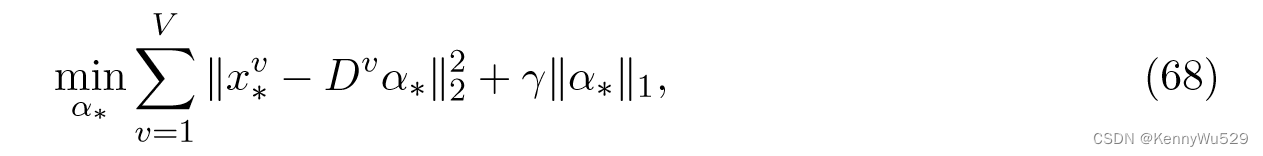
其中正则化器允许我们处理观测中的噪声。

“7.5.5 Latent Space Markov network” 7.5.5 潜在空间马尔可夫网络

在数据来自不同视图和给定一组潜在变量，响应变量是条件独立的假设下，陈等人（2010）基于通用多视图潜在空间--马尔可夫网络“Markov network” （MN）-- 构建了多视图数据共享的预测子空间。

双视图潜在空间马尔可夫网络由输入数据为 X : {Xn} 和 Z : {Zm} 的两个视图以及一组潜在变量 H : {Hk} 组成。根据随机场理论，两个视图的边际分布分别可以写成指数形式

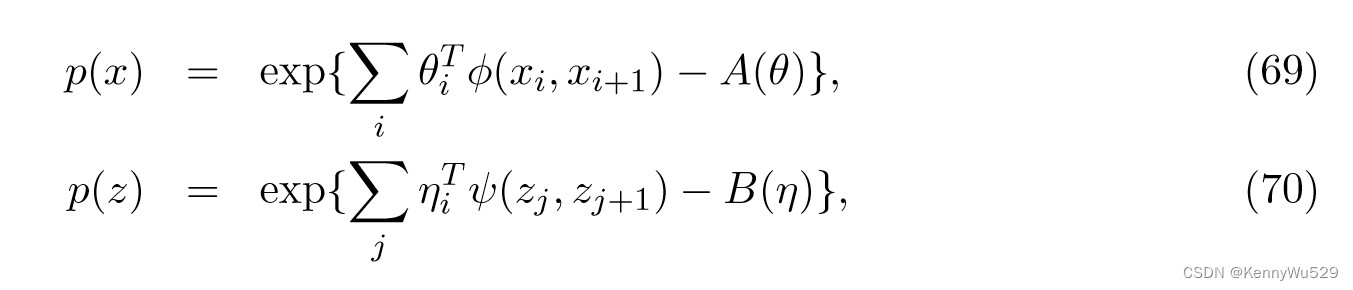
其中 φ 和 ψ 是特征函数，A 和 B 是对数配分函数。对于潜在变量，边际分布为

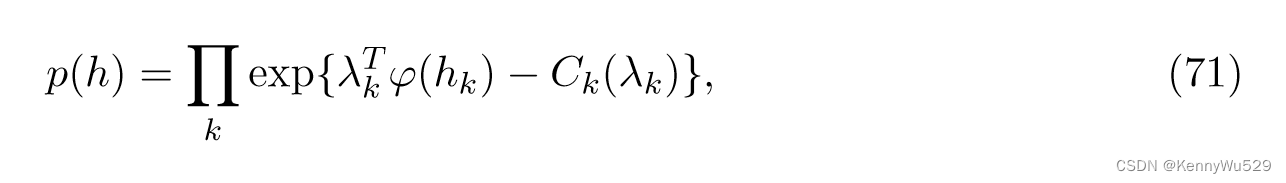
其中 φ(hk) 是 hk 的特征向量，Ck 是对数划分函数。通过在对数域中组合上述分量，联合模型分布定义为

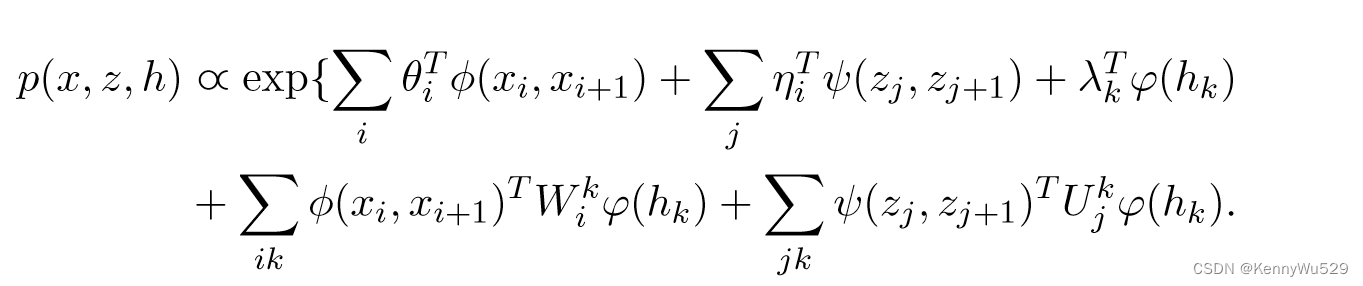
另外考虑到每个输入样本都与一个监督响应变量 y ∈ {1, · · · , T } 相关联，我们可以定义

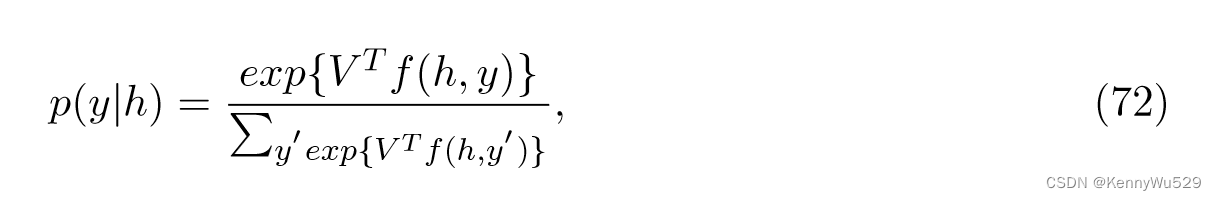
其中，f (h, y) 为特征向量，其从 (y − 1)K + 1 到 yK 的元素为 h ，其他均为 0。因此，V 是 T 个子向量 Vy 的堆叠参数向量，每个子向量其中对应于类标签 y。

尽管这种多视图潜在空间 MN 可以通过最大似然估计（MLE）来学习，Chen 等人（2010）直接以large-margin方法估计决策边界。假设判别函数 F (y, h; V ) 是线性的，即 F (y, h; V ) = V T f (h, y)，这看起来像 SVM 中的判别函数 W T X 。

机器学习算法（一）SVM_机器学习svm_不吃饭就会放大招的博客-CSDN博客

机器学习.pdf   ---- 论文/机器学习pdf中关于SVM部分

那么目标函数是

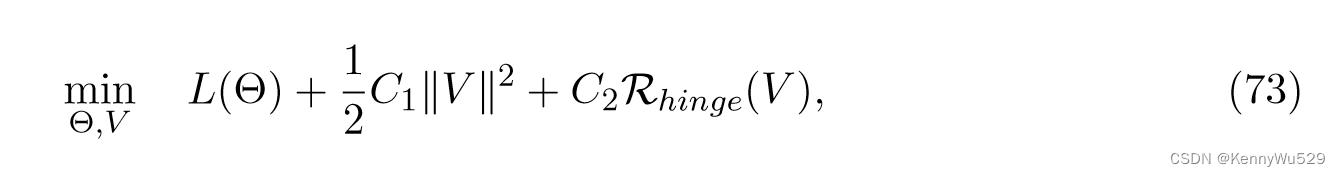
其中第一项 L(θ) = − Σ d log p(xd, zd) 是负数据似然，第二项是决策边界的约束，第三项铰链损失充当 SVM 中的松弛变量 xi 。由于方程 (73) 最大化数据似然并最小化训练损失，可以预期，通过解决这个问题，我们可以同时找到预测潜在空间表示 p(h|x, z) 和预测模型参数 V。