从中序与后序遍历序列构造二叉树

文章内容是自己刷leetcode题目的一些总结。
文章内容参考公众号： 代码随想录。
喜欢的话，希望大家可以点点赞 ^ - ^

一.题目描述

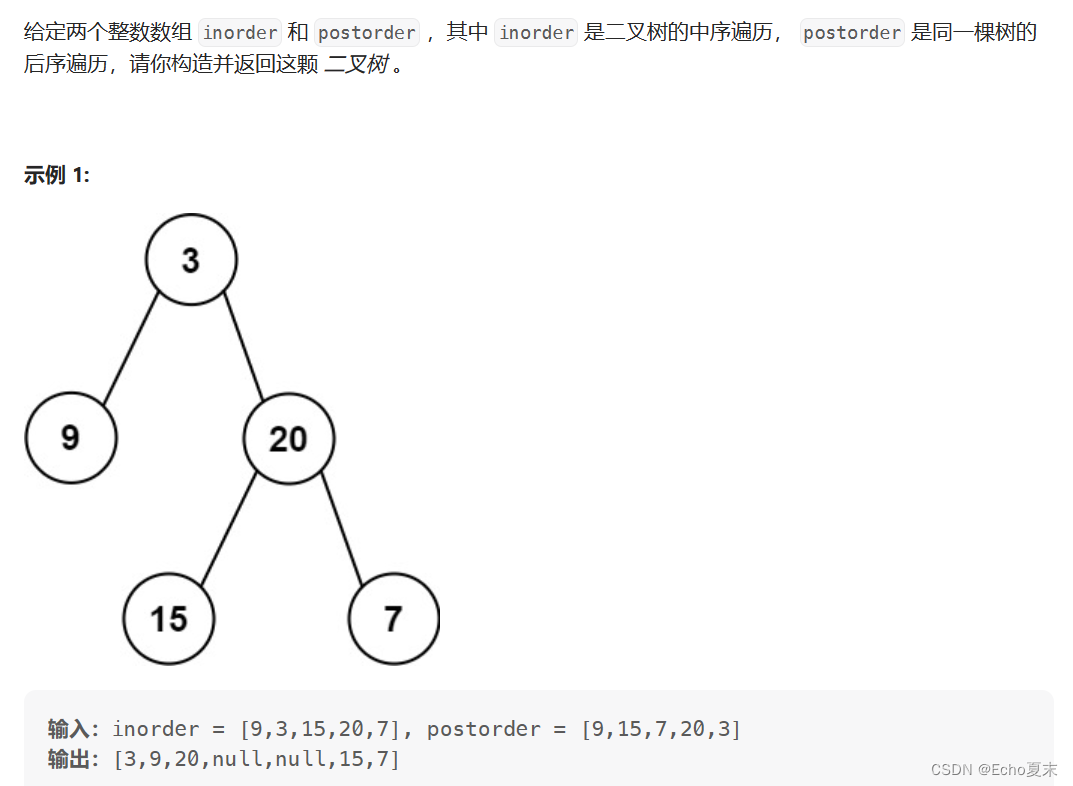
二.题目分析

我们知道中序遍历是左中右，后序遍历是左右中，那么我们可以根据中间节点在中序与后序遍历中的的位置来构造二叉树。

我们采用递归的方式来处理这道问题。

终止条件是遇到空节点终止。

在每次递归中，我们先取出根节点，也就是后序遍历的最后一个元素，那么用它构造树的根节点。

然后在中序遍历中寻找根节点的位置作为切割点，将中序遍历分为左右子树，根据中序遍历左右子树的大小来分割后序遍历，也将其分为左右区间。分割中序遍历与后序遍历为两个左右区间，他们代表的就是根节点的左右子树。

最后根据分割后的左右子树进行递归。

三.递归代码

class Solution {
public:
    TreeNode* traversalTree(vector<int>& inorder, vector<int>& postorder) {
        //空数组直接终止
        if(postorder.size() == 0) {
            return nullptr;  
        }

        //后序遍历最后一个元素为根节点
        int rootValue = postorder[postorder.size() - 1];
        TreeNode* root = new TreeNode(rootValue);

        //根据根节点在中序遍历划分左右区间
        //找切割点
        int idx;
        for(idx = 0; idx < inorder.size(); idx ++) {
            if(inorder[idx] == rootValue) break;
        }

        vector<int> inleft(inorder.begin(), inorder.begin() + idx); //左闭右开
        vector<int> inright(inorder.begin() + idx + 1, inorder.end());

        //切割后序遍历数组(利用中序遍历和后序遍历个数相同)
        postorder.resize(postorder.size() - 1); //根节点已经用过了
        vector<int> postleft(postorder.begin(), postorder.begin() + inleft.size());
        vector<int> postright(postorder.begin() + inleft.size(), postorder.end());

        //递归
        root->left = traversalTree(inleft, postleft);
        root->right = traversalTree(inright, postright);

        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(inorder.size() == 0) {
            return nullptr;  
        }
        return traversalTree(inorder, postorder);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

三.总结

通过此题我们可以知道根据一棵二叉树的中序遍历与后序遍历可以还原出这棵二叉树。

那么同样的，给出一颗二叉树的前序遍历与中序遍历也可以还原出二叉树。

但是只给出前序遍历和后序遍历无法构造出唯一的一棵二叉树。

前序和后序在本质上都是将父节点与子结点进行分离，但并没有指明左子树和右子树的能力，因此得到这两个序列只能明确父子关系，而不能确定一个二叉树。而中序遍历在知道根节点后可以指明左右子树的关系。

所以只能根据前序或者后序遍历先确定根节点，然后再利用中序遍历划分左右子树。