热门标签
热门文章
- 1正在走进现实的“飞行汽车”,能否颠覆地面交通?
- 2spring、springBoot、mybatis_spring springboot mybatis
- 3Linux 性能调优之硬件资源监控_virtio gpu
- 4关系型数据库和非关系型数据库_非关系型数据库伸缩性强
- 5esp32s3下i2s开发记录_esp32s3 i2s
- 6【Linux】解锁操作系统潜能,高效进程管理的实战技巧
- 7DES加密解密算法(简单、易懂、超级详细)
- 8配置tomcat_Tomcat配置HTTPS安全认证
- 9【跟着慕课网学习Python】(1)_慕课网中国大学mooc python
- 10超文本传输协议HTTP_具有隐私的超文本传输协议
当前位置: article > 正文
动态规划算法(C++)(3、路径问题)
作者:寸_铁 | 2024-07-15 22:33:43
赞
踩
动态规划算法(C++)(3、路径问题)
本文为动态规划算法的第3篇,前两篇主要分享一维动态规划算法。本篇将分享二维动态规划算法的用法,主要用于处理路径问题,如:不同路径,最短路径... 下面通过例题来一起学习动态规划算法吧!
一、不同路径问题(对应Leetcode62)
对应习题链接:62. 不同路径 - 力扣(LeetCode)
1.题目描述:

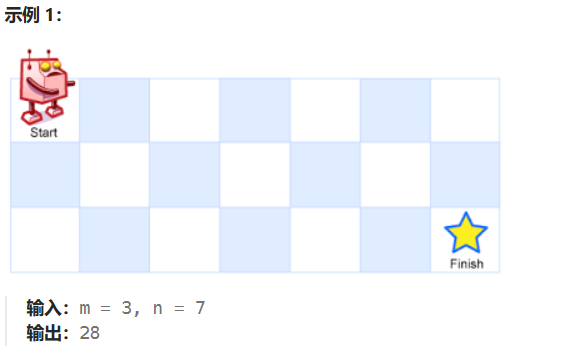
2.解题思路:
1.创建一个二维的dp表,dp[ i ][ j ]表示走到 i, j 位置时一共有多少种方法。
2.初始化问题,机器人起点(如果只有一个格子,也就是只有一条路径,所以dp[ 0 ][ 1 ]或者dp[ 1 ][ 0 ]要初始化为1,机器人此时的位置是1,1。所以要多开1行1列。)
3.解题代码:
- class Solution {
- public:
- int uniquePaths(int m, int n) {
- vector<vector<int>>dp(m+1,vector<int>(n+1)); //多开1行1列
- dp[0][1]=1;
- for(int i=1;i<=m;i++) //初始位置从1,1(假如从0,0开始循环会越界)
- {
- for(int j=1;j<=n;j++)
- {
- dp[i][j]=dp[i-1][j]+dp[i][j-1];
- }
- }
- return dp[m][n];
- }
- };
二、最小路径和(对应LeetCode64)
对应习题链接:64. 最小路径和 - 力扣(LeetCode)
1.题目描述:

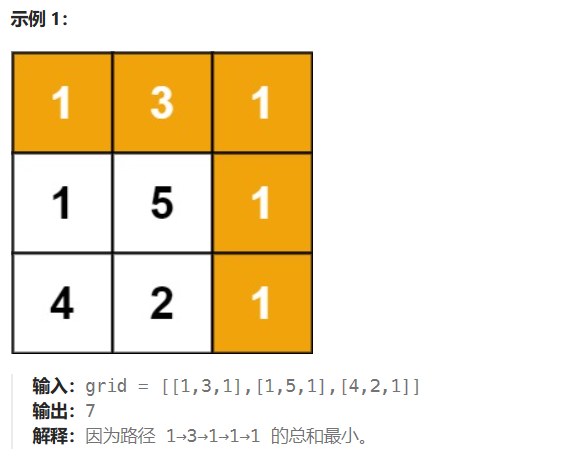
2.解题思路:
3.解题代码:
- class Solution {
- public:
- int minPathSum(vector<vector<int>>& grid) {
- int m=grid.size(),n=grid[0].size();
- vector<vector<int>>dp(m+1,vector<int>(n+1,INT_MAX));
- dp[0][1]=dp[1][0]=0;
- for(int i=1;i<=m;i++)
- {
- for(int j=1;j<=n;j++)
- {
- dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
- }
- }
- return dp[m][n];
- }
- };

总结
本篇通过两篇二维数组中的动态规划思想解决了问题,希望可以对大家的解题有所帮助,后续我会继续在本专栏更新动态规划算法的其他应用。
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/寸_铁/article/detail/831222
推荐阅读
相关标签



