devbox
小丑西瓜9
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

最近最久未使用（LRU）置换算法的C++实现_最近最久未使用算法

作者：小丑西瓜9 | 2024-02-29 04:12:34

赞

踩

最近最久未使用算法

操作系统实验 最近最久未使用（LRU）置换算法

实验题目

  1. 最近最久未使用（LRU）置换算法原理就是：当需要淘汰某页面时，选择当前一段时间内最久未使用过的页先淘汰，即淘汰距当前最远的上次使用的页。

    • 例如: 分配给该进程的页块数为3，一个20位长的页面访问序列为:12560,36536,56042,70435，则缺页次数和缺页率按下图给出:

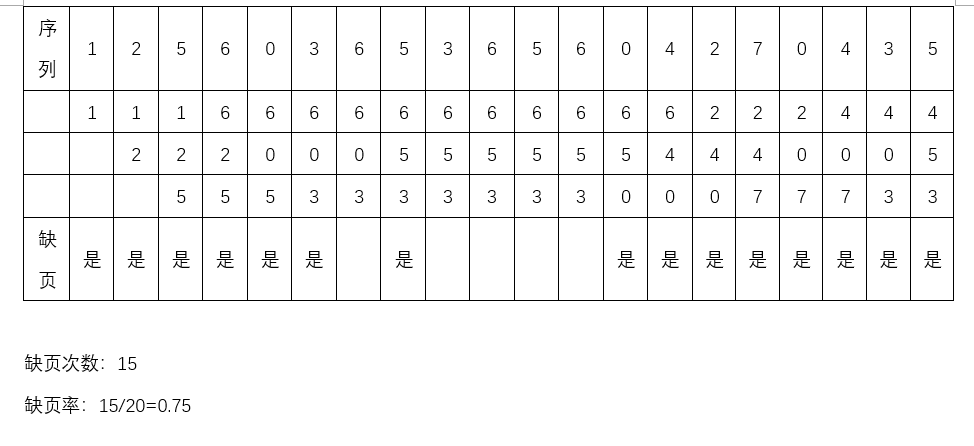
      image-20211207201735320

      注：原实验指导书上图示有误，该图为笔者制作。

  2. 假定分配给该进程的页块数为3，页面访问序列长度为20。本实验可以采用数组结构实现，首先随机产生页面序列，当发生请求调页时，若内存已满，则需要利用LRU算法，将当前一段时间内最久未使用过的页替换出去。

    • 模拟程序的算法如下图：

      image-20211207202046671

程序中使用的数据结构及符号说明

  1. 数组（数据结构）记录信息

    int memory[1001];      //记录进程内存中的页
bool flag[1001];       //标记：访问的页面是否在内存中
int l_time[1001];      //记录页面的最近使用时间
int vis[1001];         //记录访问序列
bool miss[1001];       //记录每次访问的缺页状态
int state[1001][1001]; //记录每次访问后的进程的内存页面状态

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6

  2. 整型变量

    int n;                 //进程内存的页块数
int now_num = 0;       //进程内存当前的页个数
int now_time = 0;      //当前时间(访问次数)
int m;                 //页面访问序列的长度
int miss_num = 0;      //缺页次数

    • 1
    • 2
    • 3
    • 4
    • 5

  3. 缺页率

    double miss_rate;      //缺页率

    • 1

  4. 自定义函数

    • void init()：初始化
    • void LRU(int a)：LRU算法的实现
    • void display()：输出信息

源程序及注释

#include <iostream>
#include <queue>
#include <iomanip>
using namespace std;

int n;                 //进程内存的页块数
int now_num = 0;       //进程内存当前的页个数
int now_time = 0;      //当前时间(访问次数)
int m;                 //页面访问序列的长度
int miss_num = 0;      //缺页次数
double miss_rate;      //缺页率
int memory[1001];      //记录进程内存中的页
bool flag[1001];       //标记：访问的页面是否在内存中
int l_time[1001];      //记录页面的最近使用时间
int vis[1001];         //记录访问序列
bool miss[1001];       //记录每次访问的缺页状态
int state[1001][1001]; //记录每次访问后的进程的内存页面状态

//初始化
void init()
{
	cout << "请输入分配给该进程的页块数：";
	cin >> n;
	cout << "请输入页面访问序列的长度：";
	cin >> m;
	cout << "请输入访问序列：";
	for (int i = 0; i < m; i++)
	{
		cin >> vis[i];
	}
	//进程的内存中刚开始没有页，初始化为-1
	for (int i = 0; i < n; i++)
	{
		memory[i] = -1;
	}
	//在内存中的标记初始化为false
	for (int i = 0; i < 1000; i++)
	{
		flag[i] = false;
	}
	//页面的最近使用时间初始化为0
	for (int i = 0; i < 1000; i++)
	{
		l_time[i] = 0;
	}
	return;
}

//LRU算法
void LRU(int a)
{
	//检查请求访问的页是否在进程的内存中
	if (flag[a] == false)
	{
		miss[now_time] = 1; //此次标记：缺页
		miss_num++;
		if (now_num == n) //内存已满
		{
			int min_time = 0x3f3f3f, min_num = -1;
			//在内存中的页中，最早被访问时间和最久未使用过的页在内存中的编号
			for (int i = 0; i < now_num; i++)
			{
				if (l_time[memory[i]] < min_time)
				{
					min_time = l_time[memory[i]];
					min_num = i;
				}
			}
			flag[a] = true;            //将当前访问的页“是否在内存中”的标记设为1
			flag[memory[min_num]] = 0; //将被替换的页“是否在内存中”的标记设为0
			memory[min_num] = a;       //当前页替换最久未使用过的页
		}
		else //内存未满
		{
			flag[a] = true;
			memory[now_num] = a; //当前页进入内存的下一个位置
			now_num++;           //内存中页的个数加1
		}
	}
	else
	{
		miss[now_time] = 0; //标记：未缺页
	}
	//保存内存中页面的序列
	for (int i = 0; i < n; i++)
	{
		state[now_time][i] = memory[i];
	}
	l_time[a] = now_time; //更新当前页的被访问时间为当前时间
	now_time++;           //访问完一个页面，当前时间加1
	return;
}

void display()
{
	//输出表头
	cout << "|访问|";
	int left = n - n / 2 - 1;
	int right = n / 2;
	while (left--)
		cout << "    ";
	cout << "序列";
	while (right--)
		cout << "    ";
	cout << "|是否缺页|" << endl;
	for (int i = 0; i < m; i++)
	{
		cout << "|" << setw(4) << vis[i] << "|";
		for (int j = 0; j < n; j++)
		{
			if (state[i][j] != -1)
				cout << setw(4) << state[i][j];
			else
				cout << "    ";
		}
		if (miss[i] == 1) //输出“是”和“否”比较丑
			cout << "|    1   |" << endl;
		else
			cout << "|    0   |" << endl;
	}
	cout << "缺页次数：" << miss_num << endl;
	miss_rate = (double)miss_num / m;
	cout << "缺页率：" << miss_num << "/" << m << "=" << setprecision(2) << miss_rate << endl;
	return;
}

int main()
{
	init();
	for (int i = 0; i < m; i++)
	{
		LRU(vis[i]);
	}
	display();
	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136

程序运行时的初值及运行结果

初值

分配给该进程的页块数：3

页面访问序列的长度：20

访问序列：1 2 5 6 0 3 6 5 3 6 5 6 0 4 2 7 0 4 3 5

运行结果

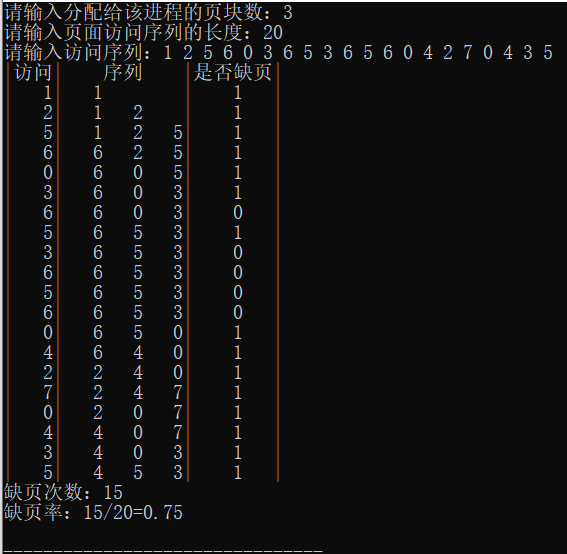
image-20211221083746165

思考题

  • 比较LRU和其他置换算法各自的优缺点，能够实现其他置换算法模拟设计，分析内存页面数的变化对各种置换算法命中率。

FIFO算法

与前文LRU算法的实现不同的是，在FIFO算法中，l_time[1001]记录页面进入内存的时间。算法实现如下：

//FIFO算法
void FIFO(int a)
{
  //检查请求访问的页是否在进程的内存中
  if (flag[a] == false)
  {
  	miss[now_time] = 1; //此次标记：缺页
  	miss_num++;
  	if (now_num == n) //内存已满
  	{
  		int min_time = 0x3f3f3f, min_num = -1; //被替换的页的入内存时间最早的页和位置
  		//在内存中的页中，先进先出（将入内存时间最早的页移出内存）
  		for (int i = 0; i < now_num; i++)
  		{
  			if (l_time[memory[i]] < min_time)
  			{
  				min_time = l_time[memory[i]];
  				min_num = i;
  			}
  		}
  		flag[a] = true;            //将当前访问的页“是否在内存中”的标记设为1
  		flag[memory[min_num]] = 0; //将被替换的页“是否在内存中”的标记设为0
  		memory[min_num] = a;       //当前页替换最早入内存的页
  	}
  	else //内存未满
  	{
  		flag[a] = true;
  		memory[now_num] = a; //当前页进入内存的下一个位置
  		now_num++;           //内存中页的个数加1
  	}
  	l_time[a] = now_time; //更新当前页的入内存时间为当前时间
  }
  else
  {
  	miss[now_time] = 0; //标记：未缺页
  }
  //保存内存中页面的序列
  for (int i = 0; i < n; i++)
  {
  	state[now_time][i] = memory[i];
  }
  now_time++; //访问完一个页面，当前时间加1
  return;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
运行结果

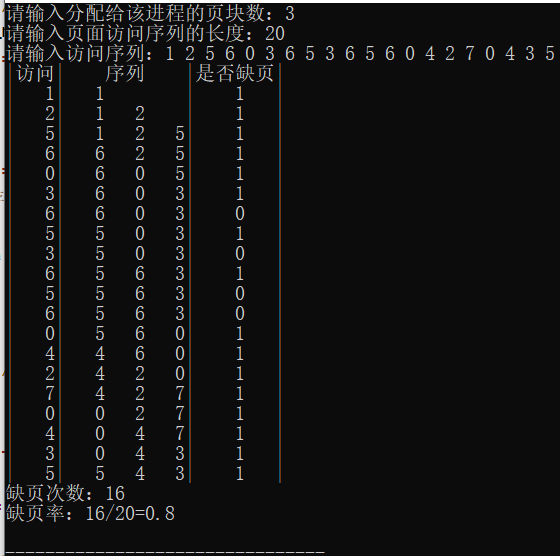
image-20211221084045884

NRU算法（CLOCK）

简单的NRU算法是给每一帧关联一个附加位，称为使用位。当某一页首次装入主存时，该帧的使用位设置为1；当该页随后再被访问到时，它的使用位置为0。

对于页替换算法，用于替换的候选帧集合看做一个循环缓冲区，并且有一个指针与之相关联。当某一页被替换时，该指针被设置成指向缓冲区中的下一帧。当需要替换一页时，操作系统扫描缓冲区，以查找使用位被置为0的一帧。每当遇到一个使用位为1的帧时，操作系统就将该位重新置为0；如果在这个过程开始时，缓冲区中所有帧的使用位均为0，则选择遇到的第一个帧替换；如果所有帧的使用位均为1,则指针在缓冲区中完整地循环一周，把所有使用位都置为0，并且停留在最初的位置上，替换该帧中的页。

int u[1001];      	   //记录页面的使用位
int point; 			   //指针

  • 1
  • 2

算法实现如下：

//NRU算法
void NRU(int a)
{
	//检查请求访问的页是否在进程的内存中
	if (flag[a] == false)
	{
		miss[now_time] = 1; //此次标记：缺页
		miss_num++;
		int num; //被替换的页的位置
		if (now_num == n) //内存已满
		{
			//指针遍历内存
			while (1)
			{
				if (u[memory[point]] == 1)
				{
					u[memory[point]] = 0; //将使用位为1的页面置为0
				}
				else //若使用位为0，被替换
				{
					num = point;
					flag[a] = true;        //将当前访问的页“是否在内存中”的标记设为1
					flag[memory[num]] = 0; //将被替换的页“是否在内存中”的标记设为0
					memory[num] = a;       //当前页替换最久未使用过的页
					break;
				}
				point++;
				if (point >= n - 1)
				{
					point %= (n - 1);
				}
			}
		}
		else //内存未满
		{
			flag[a] = true;
			memory[now_num] = a; //当前页进入内存的下一个位置
			u[now_num] = 1;	     //使用位：置为1
			now_num++;           //内存中页的个数加1
			point = now_num; 		 //指针指向下一位置
		}
	}
	else
	{
		miss[now_time] = 0; //标记：未缺页
		u[now_num] = 0;	//使用位：置为0
	}
	//保存内存中页面的序列
	for (int i = 0; i < n; i++)
	{
		state[now_time][i] = memory[i];
	}
	now_time++;           //访问完一个页面，当前时间加1
	return;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
运行结果

image-20211221092549071

最佳置换算法（OPT）（理想置换算法）

无法预知一个进程中的若干页面哪一个最长时间不被访问，故无法实现。

各算法优缺点

最近最久未使用（LRU）

优点：由于考虑程序访问的时间局部性，一般能有较好的性能；实际应用多。
缺点：实现需要较多的硬件支持，会增加硬件成本。

先进先出（FIFO）

优点：先进先出算法实现简单，是最直观的一个算法。
缺点：先进先出的性能最差，因为与通常页面的使用规则不符合，所以实际应用少。

最近不用算法（NRU/CLOCK）

优点：近似于LRU算法，考虑了时间局部性，一般性能比LRU好。
缺点：同样需要较多的硬件支持，会增加硬件成本。

最佳置换算法（OPT）（理想置换算法）

缺点：最佳置换算法是一种理想化算法，具有较好的性能，但是实际上无法实现（无法预知一个进程中的若干页面哪一个最长时间不被访问）；
优点：最佳置换算法可以保证获得最低的缺页率

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小丑西瓜9/article/detail/163644
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号