IEEE754标准

IEEE754标准

1、什么是IEEE754标准

我们知道, 计算机内部实际上只能存储或识别二进制.

在计算机中, 我们日常所使用的文档, 图片, 数字等, 在储存时, 实际上都要以二进制的形式存放在内存或硬盘中, 内存或硬盘就好像是一个被划分为许多小格子的容器, 其中每个小格子都只能盛放0或1…

我们日常使用的 浮点数 也不例外, 最终也要被存储到这样的二进制小格子中.

这就涉及到了 应该怎么存 的问题, 比如, 对于浮点数 20.5, 是应该存储为 0100011 呢, 还是应该存储为 1100110 呢?

事实上直到20世纪80年代, 还是计算机厂商各自为战, 每家都在设计自己的浮点数存储规则, 彼此之间并不兼容. 直到1985年, IEEE754标准问世, 浮点数的存储问题才有了一个通用的工业标准.

IEEE754标准提供了如何在计算机内存中,以二进制的方式存储十进制浮点数的具体标准,

IEEE754标准发布于1985年. 包括 javascript, Java, C在内的许多编程语言在实现浮点数时, 都遵循IEEE754标准.

IEEE754的最新标准是IEEE754-2008, 但本篇文章主要参考的是IEEE754-1985, 好在两者相差并不大, 而参照1985的标准可以让我们对一些基础概念有更好的理解

IEEE754提供了四种精度规范, 其中最常用的是 单精度浮点型 和 双精度浮点型 , 但IEEE754并没有规定32位浮点数类型需要叫做 float, 或64位浮点数需要叫做 double. 它只是提供了一些关于如何存储不同精度浮点数的规范和标准. 不过一般情况下, 如果我们提到 float, 其实指的就是IEEE754标准中的32位单精度浮点数. 如果我们提到 double, 其实指的就是IEEE754标准中的64位双精度浮点数

下面是单精度浮点数和双精度浮点数的一些信息, 可以先简单看一下, 看不懂也没关系, 下文会对这里的信息做详细的解释…

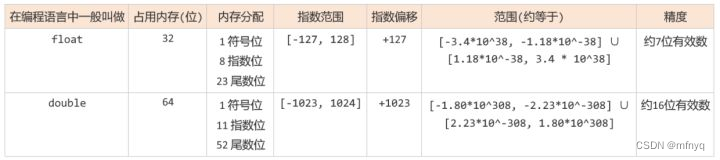
单双精度浮点数对比

好啦, 铺垫完了, 开始正文吧~

2、32位单精度浮点数在内存中的存储方式
上文说到: IEEE754标准提供了如何在计算机内存中, 以二进制的方式存储十进制浮点数的具体标准, 并制定了四种精度规范.

这里我们主要研究 32位浮点数 (或者说单精度浮点数, 或者说float类型) 在计算机中是怎么存储的. 其他精度, 比如64位浮点数, 则大同小异.

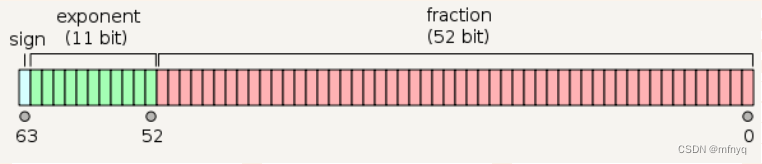
想要存储一个32位浮点数, 比如20.5, 在内存或硬盘中要占用32个二进制位 (或者说32个小格子, 32个比特位)

这32个二进制位被划分为3部分, 用途各不相同:

32位浮点数内存占用示意图, 共使用了32个小格子

这32个二进制位的内存编号从高到低 (从31到0), 共包含如下几个部分:

sign: 符号位, 即图中蓝色的方块

biased exponent: 偏移后的指数位, 即图中绿色的方块

fraction: 尾数位, 即图中红色的方块

下面会依次介绍这三个部分的概念, 用途.

1. 符号位: sign
   
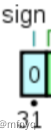
   以32位单精度浮点数为例, 以下不再赘述:

符号位: 占据最高位(第31位)这一位, 用于表示这个浮点数是正数还是负数, 为0表示正数, 为1表示负数.

举例: 对于十进制数20.5, 存储在内存中时, 符号位应为0, 因为这是个正数

2. 偏移后的指数位: biased exponent

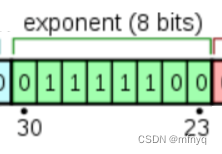
指数位占据第30位到第23位这8位. 也就是上图的绿色部分.

用于表示以2位底的指数. 至于这个指数的作用, 后文会详细讲解, 这里只需要知道: 8位二进制可以表示256种状态, IEEE754规定, 指数位用于表示[-127, 128]范围内的指数.

不过为了表示起来更方便, 浮点型的指数位都有一个固定的偏移量(bias), 用于使 指数 + 这个偏移量 = 一个非负整数. 这样指数位部分就不用为如何表示负数而担心了.

规定: 在32位单精度类型中, 这个偏移量是127. 在64位双精度类型中, 偏移量是1023. 所以, 这里的偏移量是127

⭐ 即, 如果你运算后得到的指数是 -127, 那么偏移后, 在指数位中就需要表示为: -127 + 127(偏移量) = 0

如果你运算后得到的指数是 -10, 那么偏移后, 在指数位中需要表示为: -10 + 127(偏移量) = 117

看, 有了偏移量, 指数位中始终都是一个非负整数.

看到这里, 可能会觉得还不是很清楚指数的作用到的是什么. 没关系, 让我们先继续往下看吧…

3. 尾数位:fraction
   

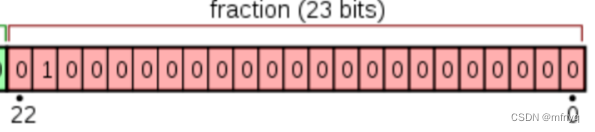
尾数位: 占据剩余的22位到0位这23位. 用于存储尾数.

在以二进制格式存储十进制浮点数时, 首先需要把十进制浮点数表示为二进制格式, 还拿十进制数20.5举例:

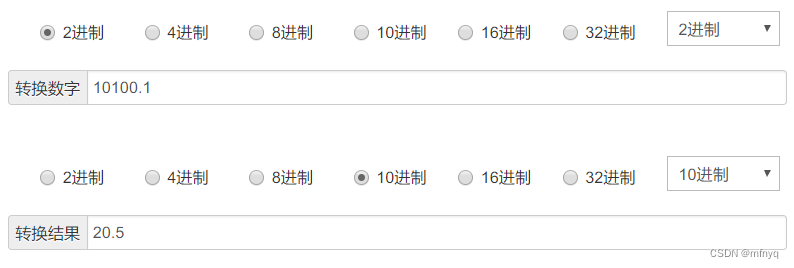
十进制浮点数20.5 = 二进制10100.1

然后, 需要把这个二进制数转换为以2为底的指数形式:

二进制10100.1 = 1.01001 * 2^4

注意转换时, 对于乘号左边, 加粗的那个二进制数1.01001, 需要把小数点放在左起第一位和第二位之间. 且第一位需要是个非0数. 这样表示好之后, 其中的1.01001就是尾数.

用 二进制数 表示 十进制浮点数 时, 表示为 尾数*指数的形式, 并把尾数的小数点放在第一位和第二位之间, 然后保证第一位数非0,这个处理过程叫做 规范化(normalized)

我们再来看看规范化之后的这个数: 1.01001 * 2^4

其中1.01001是尾数, 而4就是偏移前的指数(unbiased exponent), 上文讲过, 32位单精度浮点数的偏移量(bias)为127, 所以这里加上偏移量之后, 得到的偏移后指数(biased exponent)就是 4 + 127 = 131, 131转换为二进制就是1000 0011

现在还需要对尾数做一些特殊处理

1. 隐藏高位1.

你会发现, 尾数部分的最高位始终为1. 比如这里的 1.01001, 这是因为前面说过, 规范化之后, 尾数中的小数点会位于左起第一位和第二位之间. 且第一位是个非0数. 而二进制中, 每一位可取值只有0或1, 如果第一位非0, 则第一位只能为1. 所以在存储尾数时, 可以省略前面的 1和小数点. 只记录尾数中小数点之后的部分, 这样就节约了一位内存. 所以这里只需记录剩余的尾数部分: 01001

所以, 以后再提到尾数, 如无特殊说明, 指的其实是隐藏了整数部分1. 之后, 剩下的小数部分

2. 低位补0

有时候尾数会不够填满尾数位(即图中的红色格子). 比如这里的, 尾数01001不够23位

此时, 需要在低位补零, 补齐23位.

之所以在低位补0, 是因为尾数中存储的本质上是二进制的小数部分, 所以如果想要在不影响原数值的情况下, 填满23位, 就需要在低位补零.

比如, 要把二进制数1.01在不改变原值的情况下填满八位内存, 写出来就应该是: 1.010 0000, 即需要在低位补0

同理, 本例中因为尾数部分存储的实际上是省略了整数部分 1. 之后, 剩余的小数部分, 所以这里补0时也需要在低位补0:

原尾数是: 01001(不到23位)

补零之后是: 0100 1000 0000 0000 000 (补至23位)

3、实例: 表示十进制浮点数20.5
在上面的讨论中, 我们已经得出, 十进制浮点数 20.5 的:

符号位是: 0

偏移后指数位是: 1000 0011

补零后尾数位是: 0100 1000 0000 0000 000

现在, 把这三部分按顺序放在32位浮点数容器中, 就是 0 1000 0011 0100 1000 0000 0000 000

这就在32位浮点数容器中, 以二进制表示了一个十进制数20.5的方式

这里有一个可以验证的IEEE754浮点数内存状态的网站, 我们来验证一下:

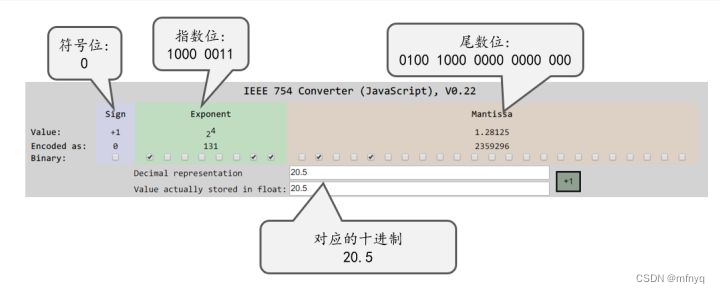
可见验证是通过的. 不过为了加深理解, 我们再反向推导一遍:

假设现在我们有一个用二进制表示的32位浮点数: 0 1000 0011 0100 1000 0000 0000 000, 求它所代表的十进制浮点数是多少?

观察可知:

符号位是0: 所以这是个正数.

尾数是: 0100 1000 0000 0000 000

去掉后面的补零, 再加上隐藏的整数部分1. 得到完整的尾数(含隐藏的整数部分)为: 1.01001

偏移后的指数位为: 1000 0011, 转换为十进制为131, 减去偏移量127, 得到真正的指数是 4

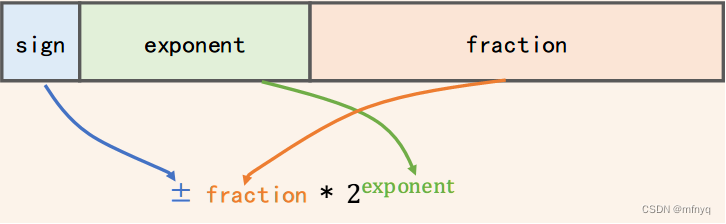
所以, 最后得到的浮点数 = 尾数(含隐藏的整数部分) * 以2为底的指数次幂

= 二进制的: 1.01001 * 2^4

= 把小数点向右移动4位

= 二进制的10100.1

= 十进制位20.5

注意, 直到最后一步才把二进制转换为十进制.

附带的, 这里还有一个进制转换网站, 可以看到二进制的10100.1, 确实等于十进制的20.5

到这里就讲解的差不多了,

随后是一张大体的计算方法示意图

还有双精度类型的内存状态示意图: