- 1c语言输出2-500的素数,C程序设计:输入2个正整数m和n(1<=m,n<=500),统计并输出m和n之间的素数个数以及这些素数的和。输入:m和...
- 2python:collisions=pygame.sprite.groupcollide(bullets,aliens,True,True)
- 3中文自然语言处理--基于 Keras 的 LSTM中文文本分类_tokenizer=tokenizer(filters='!"#$%&()*)
- 4BERT模型中的input_ids和attention_mask参数_bertmodel attention mask
- 5web前端开发零基础入门8_2、创建一个无序列表,包括10个列表项,再加一个按钮,点击按钮,隐藏或显示无序列表
- 6android屏幕适配density,Android屏幕适配方案分析
- 7Weblogic,静默安装!
- 8在苹果电脑MAC上安装Windows10(双系统安装的详细图文步骤教程)_mac装双系统win10详细教程
- 9Android Paint之 setXfermode PorterDuffXfermode 讲解_paint.setxfermode
- 10Stable Diffusion 安装教程_stablediffusion如何安装
机器学习中的数学原理——随机梯度下降法
赞
踩
这个专栏主要是用来分享一下我在机器学习中的学习笔记及一些感悟,也希望对你的学习有帮助哦!感兴趣的小伙伴欢迎私信或者评论区留言!这一篇就更新一下《白话机器学习中的数学——随机梯度下降法》!
一、什么是随机梯度下降法
随机梯度下降是随机取样替代完整的样本,主要作用是提高迭代速度,避免陷入庞大计算量的泥沼。 对于整个样本做GD又称为批梯度下降(BGD,batch gradient descent)。 随机梯度下降(SGD, stochastic gradient descent) :名字中已经体现了核心思想,随机选取一个店做梯度下降,而不是遍历所有样本后进行参数迭代。
二、算法分析
之前我们介绍过最速梯度下降法,即只要向与导数的符号相反的方向移动 x,g(x) 就会自然而然地沿着最小值的方向前进了。也就是自动更新参数。但是最速下降法除了计算花时间以外,还有一个缺点——容易陷入局部最优解。在讲解回归时,我们使用的是平方误差目标函数。这个函数形式 简单,所以用最速下降法也没有问题。现在我们来考虑稍微复杂 一点的,比如下列的图这种形状的函数:

用最速下降法来找函数的最小值时,必须先要决定从哪个 x 开始 找起。之前我们用 g(x) 说明的时候是从 x = 3 或者 x = −1 开始的,这是我们随便选择的,选用随机数作为初始值的情况比较多。不过这样每次初始值都会变,进而导致陷入局部最优解的问题。假设这张图中标记的位置就是初始值:
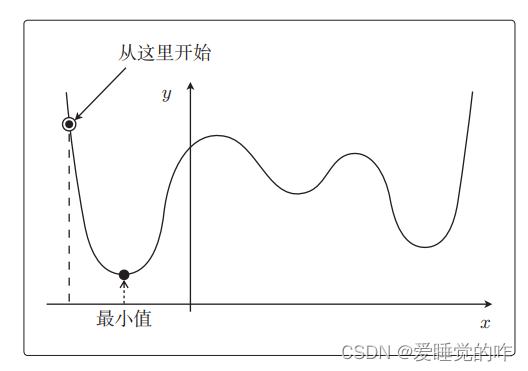
那么从这个点开始找,可以求出最小值。但是如果将下列这个点作为初始值,还没计算完就会停止,这就叫陷入了局部最优解。
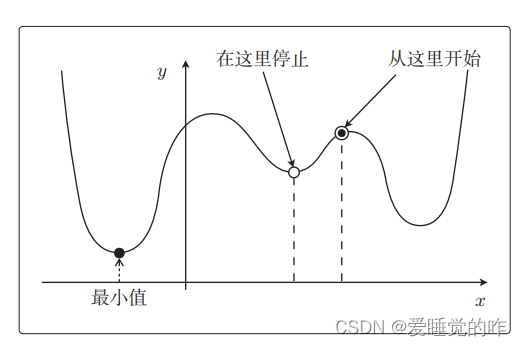
随机梯度下降法就是以最速下降法为基础的。我们先复习一下最速下降法,还记得最速下降法的参数更新表达式吗?

这个表达式使用了所有训练数据的误差,而在随机梯度下降法中会随机选择一个训练数据,并使用它来更新参数。这个表达 式中的 k 就是被随机选中的数据索引。
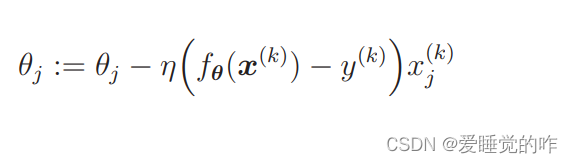
所以最速下降法更新 1 次参数的时间,随机梯度下降法可以更新 n 次,速度上明显提升。 此外,随机梯度下降法由于训练数据是随机选择的,更新参数时使用的又是选择数据时的梯度,所以不容易陷入目标函数的局部最优解。并且在实际计算过程中,的确会收敛!这样的做法就叫做随机梯度下降法!
上述提到的是随机选择1个训练数据的做法,此外还有随机选择 m 个训练数据来更新参数的做法。设随机选择 m 个训练数据的索引的集合为 K,那么我们这样来更新参数:
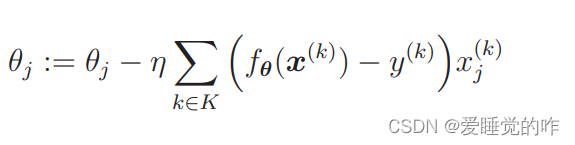
假设训练数据有 100 个,那么在 m = 10 时,创建一个有 10 个随机数的索引的集合,例如 K = {61, 53, 59, 16, 30, 21, 85, 31, 51, 10},然后重复更新参数就可以了,这样的做法称为小批量(mini-batch)梯度下降法,这是一种介于最速下降法和随机梯度下降法之间的方法。
三、总结
不管是随机梯度下降法还是小批量梯度下降法,我们都必须考虑学习率 η。把 η 设置为合适的值是很重要的。学习率的决定是一个很难的问题,可以通过反复尝试来找到合适的值,除此之外还有其他的几个办法,这是我们后续所要学习的!这三个算法总结成一句话:最速梯度下降法是用每个对应的估计值减去实际值求和,随机梯度下降法是用选定的一个估计值减去实际值求和,批量梯度下降法是用选定的多个估计值减去实际值求和。


