SCA(successive convex approximation)学习
赞
踩
参考1 https://www.zhihu.com/question/424944253
successive: 连续的含义,就是通过不断的迭代去完成的。
convex: 就是说在迭代的过程中采用的是凸函数来代替非凸函数。

参考2 https://zhuanlan.zhihu.com/p/164539842
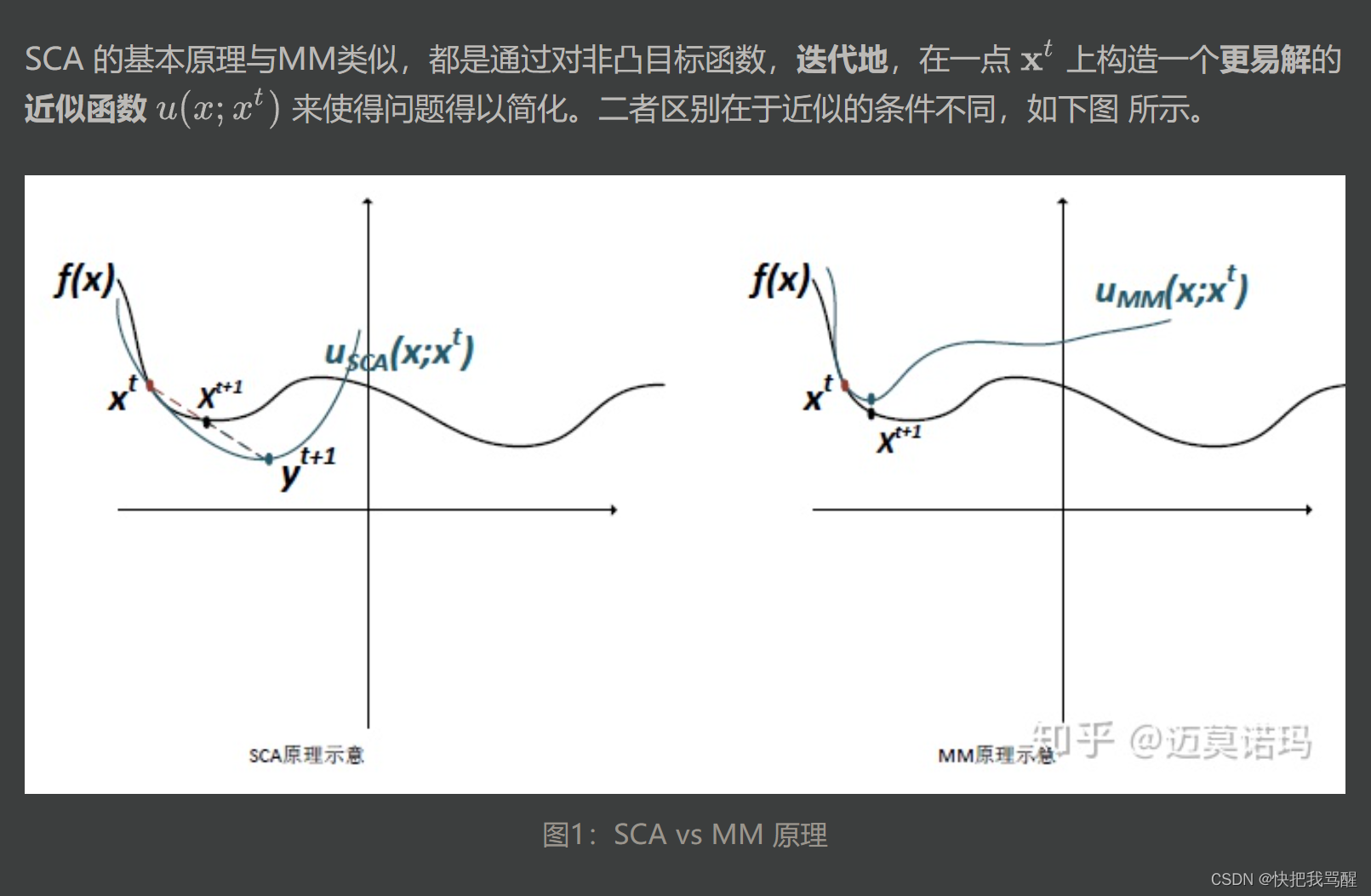

两者前三点要求相同,分别是
- 近似函数连续性
- 近似函数和原函数在近似点函数值相同
- 近似函数和原函数在近似点的一阶导数(方向导数)相同
第四点不同
SCA 要求近似函数是凸函数 而MM要求近似函数在近似点是原函数的upper bound(在原函数“上面“).
Part II A. SCA 算法
SCA的出现是为了解决实际应用中满足MM的条件的近似函数很难找的问题 (主要是第四点,满足uppder bound 又好解的近似函数很难找)。 然而根据no free lunch 的原则,我们在寻找近似函数上省了力气,就得在求解的时候付出更多力气。这是因为近似函数如果不满足upper bound那么直接取近似函数的最小值会导致“步子迈的太大”“走过了”的情况。如图1所示
y
t
+
1
y^{t+1}
yt+1为近似函数的最小值,它“超过了”目标函数的local minima. 因此需要调整步长。调整的方法非常简单,采用moving average(移动平均?),公式如下
Block Successive Convex Approximation

参考1 https://www.zhihu.com/question/424944253
successive: 连续的含义,就是通过不断的迭代去完成的。
convex: 就是说在迭代的过程中采用的是凸函数来代替非凸函数。

参考2 https://zhuanlan.zhihu.com/p/164539842


两者前三点要求相同,分别是
- 近似函数连续性
- 近似函数和原函数在近似点函数值相同
- 近似函数和原函数在近似点的一阶导数(方向导数)相同
第四点不同
SCA 要求近似函数是凸函数 而MM要求近似函数在近似点是原函数的upper bound(在原函数“上面“).
Part II A. SCA 算法
SCA的出现是为了解决实际应用中满足MM的条件的近似函数很难找的问题 (主要是第四点,满足uppder bound 又好解的近似函数很难找)。 然而根据no free lunch 的原则,我们在寻找近似函数上省了力气,就得在求解的时候付出更多力气。这是因为近似函数如果不满足upper bound那么直接取近似函数的最小值会导致“步子迈的太大”“走过了”的情况。如图1所示
y
t
+
1
y^{t+1}
yt+1为近似函数的最小值,它“超过了”目标函数的local minima. 因此需要调整步长。调整的方法非常简单,采用moving average(移动平均?),公式如下
Block Successive Convex Approximation


红框是寻找参数
α
\alpha
α的过程。
对比MM

多了搜索参数和移动平均的过程。
SCA算法的收敛



[2]的文章 Regularized Robust Estimation of Mean and Covariance Matrix Under Heavy-Tailed Distributions https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=7069228
参考4 Stochastic Successive Convex Approximation for Non-Convex Constrained Stochastic Optimization https://arxiv.org/pdf/1801.08266.pdf
论文Meisam Razaviyayn, “Successive Convex Approximation: Analysis and Applications”
https://conservancy.umn.edu/bitstream/handle/11299/163884/Razaviyayn_umn_0130E_14988.pdf?sequence=1
块坐标下降法(BCD)被广泛用于求多个块变量的连续函数f的最小值。在该方法的每次迭代中,优化单个变量块,而其余变量保持固定。为了保证BCD算法的收敛性,每个块变量的子问题需要求解到其唯一的全局最优解。不幸的是,这个要求对于许多实际场景来说常常限制性太强。在这篇论文中,我们首先研究了一种替代的非精确BCD方法,它通过连续地最小化f的一系列逼近来更新变量块,这些逼近要么是f的局部紧上界,要么是f的严格凸局部逼近。考虑不同的块选择规则,例如循环(Gauss-Seidel)、贪婪(Gauss-Southwell)、随机化或甚至多个(并行)同时块。我们刻画了这类方法的收敛条件和迭代复杂度界,特别是对于目标函数不可微或非凸的情况。同时,利用交替方向乘子法(ADMM)的思想,对存在线性约束的情况进行了简要的研究。除了确定性情形外,还研究了由随机变量参数化的代价函数的期望值最小化问题。基于逐次凸逼近思想,提出了一种非精确样本平均逼近(SAA)方法,并研究了其收敛性。我们的分析统一和推广了许多经典算法已有的收敛性结果,如BCD方法、凸函数差分(DC)方法、期望最大化(EM)算法以及经典的随机(次)梯度(SG)方法,这些算法都是大规模优化问题的流行算法.
在论文的第二部分,我们将我们提出的框架应用于两个实际问题:无线网络中的干扰管理和稀疏表示的字典学习问题。首先,研究了这些问题的计算复杂性。然后利用逐次凸近似框架,提出了求解这些实际问题的新算法。通过对真实的数据的大量数值实验对所提出的算法进行了评估。
参考4 Stochastic Successive Convex Approximation for Non-Convex Constrained Stochastic Optimization https://arxiv.org/pdf/1801.08266.pdf
https://www.cnblogs.com/kailugaji/p/11731217.html
G. Scutari, F. Facchinei, P. Song, D. P. Palomar, and J.-S. Pang, “Decomposition by partial linearization: Parallel optimization of multiuser systems,” IEEE Trans. on Signal Processing, vol. 63, no. 3, pp. 641–656, Feb. 2014.
F. Facchinei, G. Scutari, and S. Sagratella, “Parallel selective algorithms for nonconvex big data optimization,” IEEE Trans. on Signal Processing, vol. 63, no. 7, pp. 1874–1889, April 2015.


