- 1Java数据存储之---ArrayList
- 2DatawhaleAI夏令营第三期 - 基于论文摘要的文本分类与关键词抽取挑战
- 3openstack 管理 四十一 创建自己的 glance image_虚机镜像制作glance imange
- 4HW自学:蓝队初级到中级_蓝队初级要干什么
- 5[已解决]OSError: Unable to load weights from pytorch checkpoint file
- 6Doris系列1-Doris介绍
- 7鸿蒙core是什么,一文看懂HMS Core到底是什么
- 8玩客云内置EMMC存储刷入Armbian_玩客云可以刷成小主机吗
- 9Python元组:不可变的神话_fpj movie
- 10[AIGC] SQL中的数据添加和操作:数据类型介绍
第五章 图像复原与重建_图像重建
赞
踩
第五章 图像复原与重建
5.1图像复原与增强的概念
- 图像增强:是一个主观过程,我们根据自己的需求增强图片的某一部分内容
- 图像复原:客观过程,相关技术面向退化模型
5.2噪声
噪声是图像的一个重要特征,它通常表现为图像中的随机噪声和失真。
-
空间特性:通常表现为图像上的随机点、线,它们自由分布,可能影响图像的亮度、对比度等参数
-
频率特性:噪声通常是随机的,通常表现在图像的高频部分,低频部分基本不收噪声影响
-
噪声类型主要分为:高斯、瑞利、伽马、指数、均匀、椒盐,只看图像的话很难看出它们之间的区别,因此需要借助直方图
-
举例:为一张图片做“高斯噪声”处理
代码如下:import cv2 import numpy as np from matplotlib import pyplot as plt # 读取图片并转换为灰度图像 img = cv2.imread('images/circle.tif', 0) # 显示原始图片和灰度直方图 plt.subplot(121) plt.imshow(img, cmap='gray') plt.title('Original Image') plt.subplot(122) hist,bins = np.histogram(img.flatten(),256,[0,256]) plt.hist(img.flatten(),256,[0,256], color = 'r') plt.xlim([0,256]) plt.title('Histogram') plt.show() # 添加高斯噪声并显示处理后的灰度直方图 mean = 0 # 高斯分布均值为0 variance = 50 # 高斯分布标准差为50 sigma = variance ** 0.5 # sigma即为高斯函数中的标准差 gaussian_noise = np.random.normal(mean,sigma,img.shape) gaussian_noise_img = img + gaussian_noise.astype(np.uint8) plt.subplot(121) plt.imshow(gaussian_noise_img,cmap='gray') plt.title('Gaussian Noise Image') plt.subplot(122) hist,bins=np.histogram(gaussian_noise_img.flatten(),256,[0,256]) y_max=np.max(hist) for i in range(len(hist)): hist[i]=float(hist[i])/y_max cdf=hist.cumsum() # 计算累积直方图 plt.plot(cdf,color='b') plt.hist(gaussian_noise_img.flatten(),256,[0,256],color='r') plt.xlim([0,256]) plt.legend(('cdf','histogram'),loc='upper left') plt.title('Histogram after Gaussian Noise Processing') plt.show() # 进行高斯噪声处理 sigma = 2.0 img_noisy = cv2.GaussianBlur(img, (sigma, sigma), 0) # 计算高斯噪声后的灰度直方图 hist, bins, counts = cv2.countHist(img_noisy, cv2.HIST_BINARY) # 显示高斯噪声后的灰度直方图 cv2.imshow("deal_pic", hist) cv2.waitKey(0) cv2.destroyAllWindows()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
效果:
原图与直方图 
| 处理结果及其直方图 |
|---|
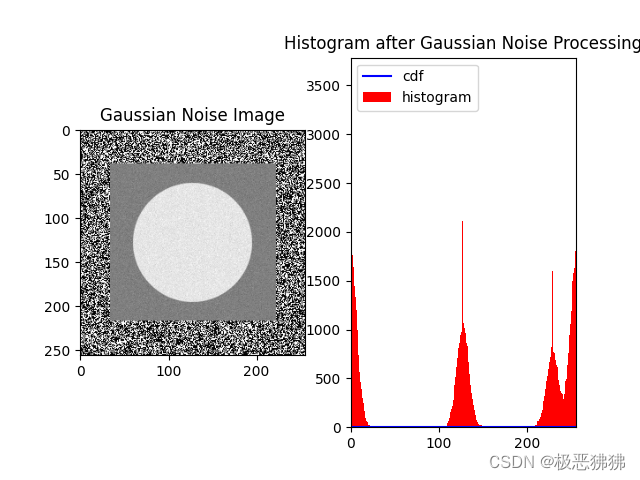 |
解析:
本实验读取一张tif图片,将其转换为RGB格式,使用Matplotlib中pyplot模块里的subplot函数创建2个subplot窗口,用于显示原图和直方图;使用 imshow 将原始图像显示在第一个 subplot 窗口中;使用hist计算、显示直方图并添加到第2个subplot窗口;
使用 NumPy 的 histogram 函数计算图像中每个灰度值出现的次数,并将其存储在变量 hist 和 bins 中。使用 plt.hist 函数将直方图显示在第二个 subplot 窗口中,并将其 x范围设置为 [0,256];
然后,添加高斯噪声到图像中。使用 np.random.normal 函数生成高斯分布的随机数,将其与原始图像相加,得到添加高斯噪声的图像。使用相同的方法计算添加高斯噪声后的图像的灰度直方图,并将其添加到第二个 subplot 窗口中;
下一步,进行高斯噪声处理。使用 OpenCV 的 GaussianBlur 函数进行高斯滤波处理,得到处理过的图像。然后,使用相同的方法计算处理过的图像的灰度直方图,并将其添加到第二个 subplot 窗口中;
最后,使用 cv2.imshow 函数显示处理后的灰度直方图
5.3空间滤波
如果图片存在噪声而没有损坏,可以考虑用“空间滤波”的方法,去除噪声、恢复图像的清晰度和细节
空间滤波:在图像的像素空间内进行操作,根据像素点附近的像素值做滤波处理。比如美颜相机里给人脸去皱,就是通过过滤掉一些深色的像素值,保留或替换浅色的像素,从而实现美白、祛疤等
均值滤波器
书本介绍了:1算术均值滤波器、2几何均值滤波器、3谐波均值滤波器、4逆谐波均值滤波器这几种;
其中:1,2适合高斯、均匀随机噪声;如果知晓噪声类型(暗、亮),则3适合处理脉冲噪声
统计排序滤波器
-
中值滤波器:是一种常见的非线性滤波器,主要原理是将像素点周围的像素值按照大小排序,取中间值作为当前像素的值,如式(1):
f ^ ( x , y ) = m e d i a n g ( s , t ) , ( s , t ) ∈ S x y (1) \hat{f}(x,y)=median{g(s,t)},(s,t)∈S_{xy}\tag1 f^(x,y)=mediang(s,t),(s,t)∈Sxy(1)
主要作用是去除图像中的椒盐噪声和斑点噪声,同时保持图像的边缘信息不被模糊化。优点是简单、快速、易于实现,适用于各种图像类型和噪声类型。缺点是对于图像中的细节信息会有一定的影响,同时处理大尺寸的图像时会降低其效率。 -
最大值和最小值滤波器:最大值滤波器的原理是将像素点周围的像素值按照大小排序,如式2所示,取最大值作为当前像素的值。这种滤波器主要用于图像中的边缘检测和图像增强;最小值滤波器的原理与最大值滤波器类似,不同的是取的是周围像素值的最小值,如式3所示,主要用于去除图像中的椒盐噪声和斑点噪声。
f ^ ( x , y ) = m a x { g ( s , t ) } , ( s , t ) ∈ S x y (2) \hat{f}(x,y)=max\{g(s,t)\},(s,t)∈S_{xy}\tag2 f^(x,y)=max{g(s,t)},(s,t)∈Sxy(2)f ^ ( x , y ) = m i n { g ( s , t ) } , ( s , t ) ∈ S x y (3) \hat{f}(x,y)=min\{g(s,t)\},(s,t)∈S_{xy}\tag3 f^(x,y)=min{g(s,t)},(s,t)∈Sxy(3)
-
举例:先对一张图片添加椒盐噪声,然后用最大值和最小值滤波器对被污染的照片进行处理
代码如下:import cv2 import numpy as np # 读取图像 img = cv2.imread("images/ax.jpg", 0) # 添加椒盐噪声 noise_img = img.copy() p = 0.1 # 假设有10% 的噪音 for i in range(noise_img.shape[0]): for j in range(noise_img.shape[1]): rdn = np.random.rand() if rdn < p/2: noise_img[i][j] = 0 # 盐噪声 elif rdn < p: noise_img[i][j] = 255 # 椒噪声 cv2.imwrite("results/jiaoyan.jpg",noise_img) img2 = cv2.imread('results/jiaoyan.jpg', 0) # 最大值滤波器 max_img = cv2.dilate(img2, np.ones((3,3),np.uint8)) # 最小值滤波器 min_img = cv2.erode(img2, np.ones((3,3),np.uint8)) # 显示经过最大值和最小值滤波处理后得到的新图像 cv2.imwrite("results/jiaoyanbig.jpg",max_img) cv2.imwrite("results/jiaoyansmall.jpg",min_img) cv2.waitKey(0)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
效果(处理结果并不符合我的预期,且可能引起不适):
原图 
| 加入椒盐噪声 |
|---|
 |
| 最大值滤波 |
|---|
 |
| 最小值滤波 |
|---|
 |
分析:我们首先用imread()函数读取一张彩色图片,并将其转换为灰度图像。然后,我们定义一个变量p来表示所添加的椒盐噪声占整幅图像的比例(例如上述代码中设置为10%),并使用两个循环遍历每个像素点,并根据随机数生成器产生的随机值以及占比参数p来决定是否给当前位置添加白色或黑色。最后,使用imshow()函数来分别显示原始图像和加入了椒盐噪声的新图像。
然后用滤波器处理,分别使用dilate()函数和erode()函数来实现最大值滤波器和最小值滤波器。其中,dilate()函数将每个像素点替换成它周围窗口内所有像素中的最大值;而erode()函数则将每个像素点替换成它周围窗口内所有像素中的最小值。
接着,我们使用imshow()函数来分别显示原始图像、经过了最大/小过滤器处理后得到的新图像,但最后的处理结果显示,噪声更离谱了。
5.4频率域滤波
频率域滤波是一种常用的图像处理方法,可以用来消除周期噪声(在一定时间内,周期性出现的噪声,容易对数据处理造成一定的干扰)。在频率域中,信号可以表示为不同频率的正弦波的叠加,所以我们可以通过将信号分解成不同频率的成分,再对每个频率成分进行滤波处理
常见的频率域滤波器包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。这些滤波器可以通过对信号的频谱进行分析,从而实现对信号的滤波处理。例如,低通滤波器可以滤除信号中的高频成分,高通滤波器则可以滤除信号中的低频成分。
讨论2种滤波器消除“周期噪声”的贡献
带阻滤波器:通常为尖锐的窄滤波器,才能在“去噪”过程中,尽可能保留原有的细节;它能抑制噪声的频率分量,如果处理的是连续稳定的信号,则不适用(稳定信号不存在周期噪声)
带通滤波器:可以在不降低信号质量的前提下,有效地抑制噪声,不能彻底消除
5.5图象复原相关技术
线性、位置不变的退化:指在图像处理中,图像的退化过程是线性的,且退化过程不随图像位置的变化而改变。这种退化过程通常可以用数学模型来描述,例如点扩散函数,这种退化可以由多种因素引起,例如光学系统的散射、运动模糊、噪声等。
估计退化函数:一般用 观察法、试验法、数学建模法
- 图像观察估计:图像增强(直方图均衡化)->目标检测->特征提取->图像分割
- 试验法:使用亮度很大的“点”来模拟冲激,对其成像,得到退化的冲激响应,变换形如H(u,v)=AG(u,v)。优点是可以更准确地估计算法参数,提高数字图像处理算法的性能指标
- 数学建模法:通过使用数学建模法,可以提高图像的质量和清晰度
逆滤波:用于恢复原始图像,其中包含了运动模糊的影响。在逆滤波中,可以使用已知的模糊函数来推导出原始图像;但是,逆滤波对加性噪声特别敏感,使得恢复的图像几乎不可用
例:处理一份由于运动造成模糊的图片
代码:
import cv2 # 读取模糊照片 img_blurry = cv2.imread('images/ydmh.jpg') # 由于运动造成的模糊 img_blurry_blur = cv2.GaussianBlur(img_blurry, (5, 5), 0) # 清晰图像 img_clear = cv2.imread('images/ydzc.jpg') # 计算模糊图像和清晰图像之间的差异 diff = cv2.absdiff(img_blurry_blur, img_clear) # 将差异图像转换为灰度图像 gray = cv2.cvtColor(diff, cv2.COLOR_BGR2GRAY) # 显示模糊照片和清晰照片 cv2.imwrite('results/1Blurry.jpg', img_blurry) cv2.imwrite('results/2Clear.jpg', img_clear) cv2.imwrite('results/3Difference.jpg', gray)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
效果:
| 运动模糊图 |
|---|
 |
| 清晰图 |
|---|
 |
| 处理结果 |
|---|
 |
实验分析:先读取由于运动造成模糊的图片和物体比较清晰的图片,再使用GaussianBlur函数模糊图像,得到一个模糊图像.使用absdiff函数计算模糊图像和清晰图像之间的差异,得到一个差异图像。最后,我们使用cvtColor函数将差异图像转换为灰度图像.
最小均方误差滤波(也叫 维纳滤波)
维纳滤波是一种基于线性时不变系统的滤波技术,其主要思想是 对数字信号进行滤波,以去除信号中的噪声和干扰。维纳滤波器是一个线性系统,该系统可以用一个线性微分方程来描述。通过求解这个线性微分方程,可以得到滤波后的信号
在维纳滤波中,信号被看作是一个复变量,并且滤波器是一个线性系统,该系统可以通过一个线性微分方程来描述。这个线性微分方程可以表示为:
d
x
d
t
=
A
x
+
b
(1)
\frac{dx}{dt} = Ax + b \tag1
dtdx=Ax+b(1)
其中,
x
x
x是信号的复变量,
t
t
t是时间,
A
A
A是滤波器的传递矩阵,
b
b
b是滤波器的输出向量。维纳滤波可以用于去除信号中的噪声和干扰,提高信号的质量和可靠性。
使用维纳滤波恢复图像清晰度的步骤如下:
1. 读入模糊图像
- 设计点扩散函数(PSF)
- 对模糊图像进行傅里叶变换
- 对PSF进行傅里叶变换
- 计算维纳滤波器的频率响应
- 对模糊图像和维纳滤波器进行卷积
- 对卷积结果进行傅里叶反变换
- 取反变换结果的实部作为恢复后的图像
约束最小二乘方滤波
该算法通过最小化目标函数来寻找最优滤波器,该目标函数考虑到图像中的噪声和图像本身的特征。
具体来说,约束最小二乘方滤波在求解滤波器时,考虑了图像中的像素值相关性,即像素之间的相邻关系。该算法使用一组约束条件来确保滤波器不会破坏图像中的像素值相关性,从而保留图像的细节和特征。这些约束条件可以通过像素之间的相关性或结构信息来定义。约束最小二乘方滤波的核心是解决退化函数对噪声的敏感性问题。降低噪声敏感的一种方法是,以平滑度量的最佳复原为基础,如图像的二阶导数(拉普拉斯算子),其数学描述是求一个带约束条件的准则函数的最小值:式(1)为最小准则函数C,式(2)为约束条件
C
=
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
[
▽
2
f
(
x
,
y
)
]
2
(1)
C=\sum^{M-1}_{x=0}\sum^{N-1}_{y=0}[\bigtriangledown^2f(x,y)]^2\tag1
C=x=0∑M−1y=0∑N−1[▽2f(x,y)]2(1)
∣ ∣ g − H f ^ ∣ ∣ 2 = ∣ ∣ η ∣ ∣ 2 (2) ||g-H\hat{f}||^2=||η||^2\tag2 ∣∣g−Hf^∣∣2=∣∣η∣∣2(2)
流程:
- 预处理:对图像进行预处理,如去除噪声、图像增强等。
- 求解滤波器:使用约束最小二乘法求解最优滤波器。
- 滤波:使用求解的滤波器对图像进行滤波。
- 后处理:对滤波后的图像进行后处理,如图像增强、恢复等。
例:比较维纳滤波与约束最小二乘方滤波(借鉴于CSDN)
代码:
import numpy as np import matplotlib.pyplot as plt import cv2 def getMotionDsf(shape, angle, dist): xCenter = (shape[0] - 1) / 2 yCenter = (shape[1] - 1) / 2 sinVal = np.sin(angle * np.pi / 180) cosVal = np.cos(angle * np.pi / 180) PSF = np.zeros(shape) # 点扩散函数 for i in range(dist): # 将对应角度上motion_dis个点置成1 xOffset = round(sinVal * i) yOffset = round(cosVal * i) PSF[int(xCenter - xOffset), int(yCenter + yOffset)] = 1 return PSF / PSF.sum() # 归一化 def makeBlurred(image, PSF, eps): # 对图片进行运动模糊 fftImg = np.fft.fft2(image) # 进行二维数组的傅里叶变换 fftPSF = np.fft.fft2(PSF) + eps fftBlur = np.fft.ifft2(fftImg * fftPSF) fftBlur = np.abs(np.fft.fftshift(fftBlur)) return fftBlur def wienerFilter(input, PSF, eps, K=0.01): # 维纳滤波,K=0.01 fftImg = np.fft.fft2(input) fftPSF = np.fft.fft2(PSF) + eps fftWiener = np.conj(fftPSF) / (np.abs(fftPSF) ** 2 + K) imgWienerFilter = np.fft.ifft2(fftImg * fftWiener) imgWienerFilter = np.abs(np.fft.fftshift(imgWienerFilter)) return imgWienerFilter def getPuv(image): h, w = image.shape[:2] hPad, wPad = h - 3, w - 3 pxy = np.array([[0, -1, 0], [-1, 4, -1], [0, -1, 0]]) pxyPad = np.pad(pxy, ((hPad // 2, hPad - hPad // 2), (wPad // 2, wPad - wPad // 2)), mode='constant') fftPuv = np.fft.fft2(pxyPad) return fftPuv def leastSquareFilter(image, PSF, eps, gamma=0.01): # 约束最小二乘方滤波 fftImg = np.fft.fft2(image) fftPSF = np.fft.fft2(PSF) conj = fftPSF.conj() fftPuv = getPuv(image) # absConj = np.abs(fftPSF) ** 2 Huv = conj / (np.abs(fftPSF) ** 2 + gamma * (np.abs(fftPuv) ** 2)) ifftImg = np.fft.ifft2(fftImg * Huv) ifftShift = np.abs(np.fft.fftshift(ifftImg)) imgLSFilter = np.uint8(cv2.normalize(np.abs(ifftShift), None, 0, 255, cv2.NORM_MINMAX)) # 归一化为 [0,255] return imgLSFilter # # 读取原始图像 img = cv2.imread("images/ydzc.jpg", 0) # flags=0 读取为灰度图像 hImg, wImg = img.shape[:2] # 带有噪声的运动模糊 PSF = getMotionDsf((hImg, wImg), 45, 100) # 运动模糊函数 imgBlurred = np.abs(makeBlurred(img, PSF, 1e-6)) # 生成不含噪声的运动模糊图像 scale = 0.01 # 噪声方差 noisy = imgBlurred.std() * np.random.normal(loc=0.0, scale=scale, size=imgBlurred.shape) # 添加高斯噪声 imgBlurNoisy = imgBlurred + noisy # 带有噪声的运动模糊 imgWienerFilter = wienerFilter(imgBlurNoisy, PSF, scale, K=0.01) # 对含有噪声的模糊图像进行维纳滤波 imgLSFilter = leastSquareFilter(imgBlurNoisy, PSF, scale, gamma=0.01) # 约束最小二乘方滤波 plt.figure(figsize=(9, 7)) plt.subplot(231), plt.title("blurred image (dev=0.01)"), plt.axis('off'), plt.imshow(imgBlurNoisy, 'gray') plt.subplot(232), plt.title("Wiener filter"), plt.axis('off'), plt.imshow(imgWienerFilter, 'gray') plt.subplot(233), plt.title("least square filter"), plt.axis('off'), plt.imshow(imgLSFilter, 'gray') scale = 0.1 # 噪声方差 noisy = imgBlurred.std() * np.random.normal(loc=0.0, scale=scale, size=imgBlurred.shape) # 添加高斯噪声 imgBlurNoisy = imgBlurred + noisy # 带有噪声的运动模糊 imgWienerFilter = wienerFilter(imgBlurNoisy, PSF, scale, K=0.01) # 维纳滤波 imgLSFilter = leastSquareFilter(imgBlurNoisy, PSF, scale, gamma=0.1) # 约束最小二乘方滤波 plt.subplot(234), plt.title("blurred image (dev=0.1)"), plt.axis('off'), plt.imshow(imgBlurNoisy, 'gray') plt.subplot(235), plt.title("Wiener filter"), plt.axis('off'), plt.imshow(imgWienerFilter, 'gray') plt.subplot(236), plt.title("least square filter"), plt.axis('off'), plt.imshow(imgLSFilter, 'gray') plt.tight_layout() plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
实验效果:

实验步骤:
1.导入一副比较清晰的图像,调整为灰度图像以便后期处理。读取其长宽,设置PDF函数及其参数,生成不含噪声的运动模糊图片
2.设置一个方差为0.01的高斯噪声添加到原图
3.分别用维纳滤波器和最小二乘方滤波器处理模糊图像
4.将噪声方差调整为0.1,重复2,3步骤
实验分析:
函数 getMotionDsf,用于生成运动模糊的点扩散函数, makeBlurred,用于对输入图像进行运动模糊处理,wienerFilter,实现维纳滤波的算法,getPuv,用于生成一个二维数组, leastSquareFilter实现了约束最小二乘方滤波的算法。实验表明:最小二乘方滤波在处理中高等噪声图像时有不俗的效果,参数合适的话效果至少优于维纳滤波。
5.6由投影重建图像
投影重建图像是指通过将三维场景投影到二维平面上,来重建图像的过程。其基本原理是将三维场景中的点、边或面在二维平面上投影,然后通过这些信息来重构二维图像
雷登变换
这是一种 用于将 三维空间中的点或多边形 转换为 二维平面上的点 的数学变换。雷登变换可以用于将三维模型转换为二维图像,反之亦可。
傅里叶切片定理
设 D D D是一个无限大的离散集合,信号可以表示为以下形式:
f ( x ) = ∑ k = 0 ∞ a k cos ( 2 π k x ) + i ∑ k = 0 ∞ b k sin ( 2 π k x ) f(x) = \sum_{k=0}^{\infty} a_k \cos(2\pi k x) + i\sum_{k=0}^{\infty} b_k \sin(2\pi k x) f(x)=k=0∑∞akcos(2πkx)+ik=0∑∞bksin(2πkx)
如果把区域 D D D切割成很多的小片,并且在每个切片上定义一个函数 f s ( x ) f_s(x) fs(x),使得 f s ( x ) f_s(x) fs(x) 在切片上的值域是 [ − 1 , 1 ] [-1,1] [−1,1],那么这些函数 f s ( x ) f_s(x) fs(x) 可以等价于 f ( x ) f(x) f(x) 在整个 D D D 上的傅里叶展开。具体地, f s ( x ) f_s(x) fs(x) 可以表示为以下形式的傅里叶级数:
f s ( x ) = ∑ k = 0 ∞ a s k cos ( 2 π k x ) + i ∑ k = 0 ∞ b s k sin ( 2 π k x ) f_s(x) = \sum_{k=0}^{\infty} a_{sk} \cos(2\pi k x) + i\sum_{k=0}^{\infty} b_{sk} \sin(2\pi k x) fs(x)=k=0∑∞askcos(2πkx)+ik=0∑∞bsksin(2πkx)
其中, a s k a_{sk} ask 和 b s k b_{sk} bsk 是 f s ( x ) f_s(x) fs(x) 在切片 s s s 上的系数,满足与 a k a_k ak 和 b k b_k bk 相同的条件。
平行射线束滤波反投影的重建
计算反投影前,先做简单的滤波,能够避免部分“模糊的结果”,如式(1)所示
f
(
x
,
y
)
=
∫
−
∞
∞
∫
−
∞
∞
F
(
u
,
v
)
e
j
2
π
(
u
x
+
v
y
)
d
u
d
v
(1)
f(x,y) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} F(u,v) e^{j2π(ux+vy)}du dv\tag1
f(x,y)=∫−∞∞∫−∞∞F(u,v)ej2π(ux+vy)dudv(1)
使用傅里叶切边定理有式(2),范围是[0,360],可拆分成[0,180]与[180,360]
f
(
x
,
y
)
=
∫
0
2
π
∫
0
∞
G
(
w
,
θ
)
e
j
2
π
w
(
x
c
o
s
θ
+
y
s
i
n
θ
)
w
d
w
d
θ
(2)
f(x,y) = \int_{0}^{2π} \int_{0}^{\infty} G(w,θ) e^{j2πw(xcosθ+ysinθ)}wdw dθ\tag2
f(x,y)=∫02π∫0∞G(w,θ)ej2πw(xcosθ+ysinθ)wdwdθ(2)
平行射线束滤波反投影的重建过程可以分为以下几个步骤:
- 平行射线束投影:将输入的图像通过一组平行射线束投影到二维平面上。
- 滤波:对投影到二维平面上的射线束图像进行滤波,以去除噪声和不必要的细节。
- 反投影:将滤波后的图像从二维平面上反投影回三维空间中。
- 重建:通过计算反投影后的图像与真实三维图像之间的差异,然后使用误差函数进行优化,以最小化差异。


