计算智能——蚁群算法_蚁群算法伪代码

蚁群算法

1、基本原理

蚁群算法是对自然界蚂蚁的寻径方式进行模似而得出的 一种仿生算法：蚂蚁在运动过程中，能够在它所经过的路 径上留下信息素(pheromone)的物质进行信息传递，而蚂蚁在运动过程中能够感知这种物质，并以此指导自己的 运动方向。由大量蚂蚁组成的蚁群集体行为便表现出一种信息正反馈现象：某一路径上走过的蚂蚁越多，则后来者选择该路径的概率就越大。

2、基本概念和流程

在ACO 算法中，人工蚂蚁实际上代表的是一个解的随机构建过程，从最初的空解开始，通过不断地向部分解添加解的成分而构建出一个完整的解。
• 解的构建：每只蚂蚁最初都从随机选择出来的城市出发，每经过一次迭代蚂蚁就向解中添加一个还没有访问过的城市。当所有城市都被蚂蚁访问过之后，解的构建就终止。对于每只蚂蚁k，路径记忆向量按照访问顺序记录了所有k已经经过的城市序号。设蚂蚁k当前所在城市为i， 则其选择城市j作为下一个访问对象的概率为：

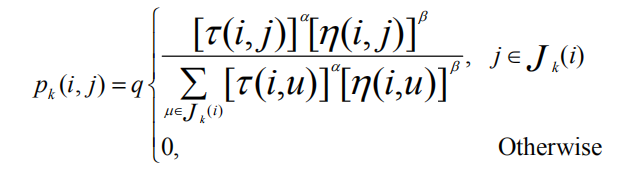
• 信息素更新：这里m是蚂蚁个数, ρ是信息素的蒸发率，规定0≤ρ≤1,在AS中通常设置为ρ=0.5，△ζ_ij是第k只蚂蚁在它经过的边上释放的信息素量，它等于蚂蚁k本轮构建路径长度的倒数。C表示路径长度，它是R^k中所有边的长度和。

3、流程图和伪代码

4、代码实现

%% 导入数据
load citys_data.mat

%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \n');
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
    for j = 1:n
        if i ~= j
            D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
        else
            D(i,j) = 1e-4;      
        end
    end    
end

%% 初始化参数
fprintf('Initializing Parameters... \n');
m = 75;                              % 蚂蚁数量
alpha = 1;                           % 信息素重要程度因子
beta = 5;                            % 启发函数重要程度因子
rho = 0.5;                           % 信息素挥发因子
Q = 1;                               % 常系数
Eta = 1./D;                          % 启发函数
Tau = ones(n,n);                     % 信息素矩阵
Table = zeros(m,n);                  % 路径记录表
iter = 1;                            % 迭代次数初值
iter_max = 160;                      % 最大迭代次数 
Route_best = zeros(iter_max,n);      % 各代最佳路径       
Length_best = zeros(iter_max
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30