- 1【python】python二手房数据抓取分析可视化(源码)【独一无二】_基于python的xx地区二手房数据采集与可视化分析
- 2Macbook M1使用vscode+iverilog+gtkwave实现Verilog代码的编译与运行
- 3PyTorch指标计算库TorchMetrics详解_pytorchlighning torchmetrics f1
- 4大众点评文字反爬_大众点评爬数据 页面数据会二次刷新
- 5大数据01-Hadoop3.3.1伪分布式安装_hadoop伪分布式安装
- 6未来的云计算基础设施长什么样?
- 7基于Echarts的超市销售可视化分析系统(数据+程序+论文)
- 8【愚公系列】2024年03月 《AI智能化办公:ChatGPT使用方法与技巧从入门到精通》 033-ChatGPT的更多场景应用(ChatGPT+教育)
- 9推荐系统-概述:基本架构_推荐系统 实时特征
- 10SpringBoot--热部署--方案_
true
数学建模——评价模型
赞
踩
一.模糊综合评价模型
1.基础知识
模糊子集的隶属函数:设
U
U
U是论域(论域是指对象的不空集合)则称定义在论域
U
U
U上的映射
A
(
x
)
A(x)
A(x)为模糊子集A的隶属函数。隶属函数的值域是
[
0
,
1
]
[0,1]
[0,1],反映的是模糊子集中的元素
x
x
x对论域中某个元素的隶属度。当
A
(
x
)
=
1
A(x)=1
A(x)=1说
x
x
x隶属,当
A
(
x
)
=
0
A(x)=0
A(x)=0说明
x
x
x不隶属,值取在
(
0
,
1
)
(0,1)
(0,1)则反映的是隶属于论域某个元素的真实程度。
矩阵的模糊运算:
∧
\wedge
∧表示逻辑乘法 ,
∨
\vee
∨表示逻辑加法。前者取左右操作数中小的一个,后者取左右操作数中大的一个。
2.一级模糊综合评价
一级模糊综合评价是指评价因素较少,评价指标只有一级的情况下的模糊综合评价。
一级模糊综合评价的基本步骤:
得到的评价结果向量R反映的是评价对象对于各个评语的隶属度。
示例:有甲乙丙三项科研成果,使用模糊综合评价模型从中选出最优秀的一项成果。
| 项目 | 科技水平 | 实现可能性 | 经济效益 |
|---|---|---|---|
| 甲 | 国际先进 | 70% | >100万 |
| 乙 | 国内先进 | 100% | >200万 |
| 丙 | 一般 | 100% | >20万 |
(1)定性评价指标值的量化。假设通过专家打分的方式记录各个评语占比的方式得到如下定性指标量化后的指标值:
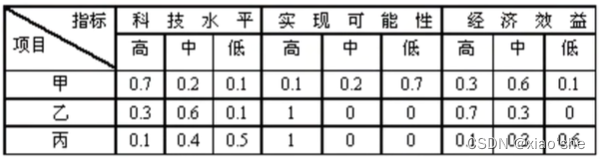
(2)确定评价指标集合A和评语集合B。有
A
=
{
科技水平,实现可能性,经济效益
}
A=\{科技水平,实现可能性,经济效益\}
A={科技水平,实现可能性,经济效益},
B
=
{
高,中,低
}
B=\{高,中,低\}
B={高,中,低}。
(3)求各个评价对象的模糊评价矩阵
P
(
x
)
=
{
P
i
j
}
P(x)=\{P_{ij}\}
P(x)={Pij},其中
P
i
j
P_{ij}
Pij的含义是评价对象
x
x
x在第
i
i
i个评价指标下对于第
j
j
j个评语的隶属度。这里隶属度用各个评语占比表示。于是可知一个评价对象的模糊评价矩阵的形状
(
m
,
n
)
(m,n)
(m,n)满足
m
=
评价指标集大小
,
n
=
评语集大小
m=评价指标集大小,n=评语集大小
m=评价指标集大小,n=评语集大小。有:
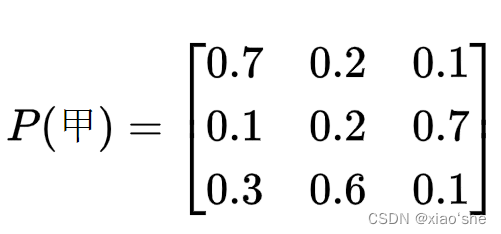
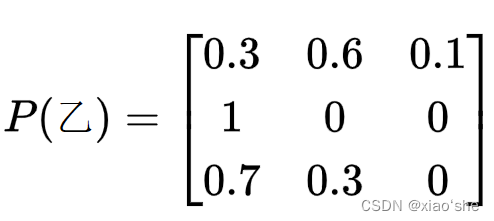
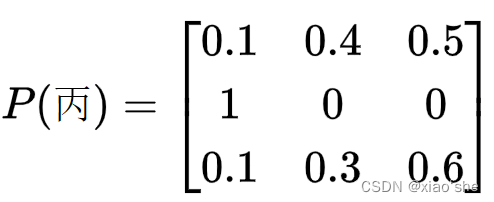
(4)确定指标权重系数向量。假设通过成对比较法得到权重向量
W
=
(
0.2
,
0.3
,
0.5
)
W=(0.2,0.3,0.5)
W=(0.2,0.3,0.5)。
(5)利用矩阵模糊运算得到评价结果向量
R
R
R,其中
R
=
W
P
R=WP
R=WP。有:

评价结果向量的含义是对象 x x x隶属于评语 B j , j = 0 , 1... , l e n ( B ) B_{j},j=0,1...,len(B) Bj,j=0,1...,len(B)的可信程度。分析评价结果向量可知对于甲大多数专家的评价是中的;对于乙大多数专家的评价是高的;对于丙大多数专家的评价是不好的。于是最佳的科研项目应该是乙。
3.二级模糊综合评价
二级模糊综合评价是指由于评价因素较多使得评价指标分为两级的模糊综合评价。例如使用模糊综合评价方法评价一个人是不是男神,有评价指标集
A
=
{
五官
,
身体条件,发展前景
}
A=\{五官,身体条件,发展前景\}
A={五官,身体条件,发展前景}。而又有
五官
=
{
耳,眉,眼,鼻,唇
}
五官=\{耳,眉,眼,鼻,唇\}
五官={耳,眉,眼,鼻,唇},
身体条件
=
{
身高,体重,体力
}
身体条件=\{身高,体重,体力\}
身体条件={身高,体重,体力}。这就构成了二级的评价指标。类似的还有
n
n
n级评价指标,对应着
n
n
n级模糊评价问题。
n
n
n级模糊评价模型与二级不尽相同,会二级就会
n
n
n级。二级模糊评价模型可以理解为一级模糊评价模型中嵌套了一个一级模糊评价模型。内部的模糊评价模型得到的结果是一级指标的评价结果。而一级指标的评价结果就可以作为评价对象该指标的评价指标值了。
二级模糊评价模型步骤:
示例 使用模糊综合评价模型来判断一个电视剧品牌好不好。评价因素有平面图像,3D图像,立体声,重低音,价格。其中对于平面图像30%的人认为很好,20%人人为较好,40%人人为一般,10%人认为不好。对于3D图像40%人认为很好,50%人认为较好,10%人认为一般,没有人认为不好。对于立体声10%人认为很好,20%人认为较好,20%人认为一般,50%人认为不好。对于重低音30%人认为很好,10%人认为较好,10%的人认为一般,50%的人认为不好。对于价格的评价为10%认为很好接受,10%认为还可以接受,30%人认为勉强接受,50%人认为很难以接受。
解:假设通过成对比较法确定的权重向量有:{平面图像,3D图像}=(0.3,0.7),{立体声,重低音}=(0.4,0.6),{图像,声音,价格}=(0.5,0.3,0.2)。
(1)确定评价指标
A
=
{
图像,声音,价格
}
,
图像
=
{
平面图像,
3
D
图像
}
A=\{图像,声音,价格\},图像=\{平面图像,3D图像\}
A={图像,声音,价格},图像={平面图像,3D图像}
(2)取得评语集B
B
=
{
很好,较好,一般,不好
}
B=\{很好,较好,一般,不好\}
B={很好,较好,一般,不好}
(3)一级指标模糊评价矩阵(提示:一级指标通过二级指标评价)


(4)用矩阵模糊运算得到一级指标评价结果向量R2,其中
R
2
=
W
2
P
2
R2=W2P2
R2=W2P2。


(5)根据一级指标评价结果向量写出关于对象的模糊评价矩阵
P
1
P1
P1.

(6)利用矩阵模糊运算得到关于对象的评价结果向量

根据结果分析大多数人认为这台电视机是较好的。所以认为这台电视剧品质属于较好。
二.灰色关联分析模型
1.灰色关联分析原理
灰色关联分析的原理是选择一个理想的比较标准(参考列),计算比较列和参考列的关联度(反映参考列和比较列间的关系紧密程度)。关联度越大则说明比较列越接近理想的指标值,那它就更好。
2.灰色关联分析步骤
(1)根据评价目的确定评价的指标体系。比如我要评价大学老师好不好,那么指标可选择为教学质量和科研水平等等。收集评价数据。形成如下矩阵:
设有
m
m
m个评价指标
n
n
n个评价对象。则
x
i
j
,
i
=
1
,
2
,
.
.
.
,
m
.
j
=
1
,
2
,
.
.
.
,
n
x_{ij},i=1,2,...,m.j=1,2,...,n
xij,i=1,2,...,m.j=1,2,...,n表示第
j
j
j个评价对象的第
i
i
i个评价指标值。
X
=
{
x
i
j
}
,
i
=
1
,
2
,
.
.
.
,
m
.
j
=
1
,
2
,
.
.
.
,
n
.
X=\{x_{ij}\},i=1,2,...,m.j=1,2,...,n.
X={xij},i=1,2,...,m.j=1,2,...,n.
(2)确定参考列,参考列
X
o
=
(
x
01
,
x
02
,
.
.
.
,
x
0
m
)
T
X_{o}=(x_{01},x_{02},...,x_{0m})^T
Xo=(x01,x02,...,x0m)T.参考列的各个元素可以选择各个指标的最优值。
(3)计算关联系数
ξ
i
j
\xi _{ij}
ξij(是第
i
i
i个对象的第
j
j
j个指标的相对于参考序列
X
0
X_{0}
X0的第
j
j
j个值的关联系数)。计算公式如下:
ξ
i
j
=
m
i
n
i
m
i
n
j
∣
x
0
j
−
x
i
j
∣
+
ρ
m
a
x
i
m
a
x
j
∣
x
o
j
−
x
i
j
∣
∣
x
0
j
−
x
i
j
∣
+
ρ
m
a
x
i
m
a
x
j
∣
x
o
j
−
x
i
j
∣
\xi _{ij}=\frac{\underset{i}{min} \underset{j}{min}\left | x_{0j}-x_{ij} \right | +\rho\underset{i}{max}\underset{j}{max}\left | x_{oj}-x_{ij} \right | }{\left | x_{0j}-x_{ij} \right | +\rho\underset{i}{max}\underset{j}{max}\left | x_{oj}-x_{ij} \right |}
ξij=∣x0j−xij∣+ρimaxjmax∣xoj−xij∣iminjmin∣x0j−xij∣+ρimaxjmax∣xoj−xij∣
注:其中
ρ
\rho
ρ表示分辨系数,它的取值影响到关联系数间的区分度,取值在(0,1)之间,越接近1计算得到的关联系数差距越大。一般这个参数就设为0.5.
(4)计算第
i
i
i个比较列对参考列的关联度
r
o
i
r_{oi}
roi,计算公式如下:
r
0
i
=
1
m
∑
j
=
1
m
ξ
i
j
,
(
i
=
1
,
2
,
.
.
.
,
n
.
j
=
1
,
2
,
.
.
.
,
m
)
r_{0i}=\frac{1}{m}\sum_{j=1}^{m}\xi_{ij} ,(i=1,2,...,n.j=1,2,...,m)
r0i=m1j=1∑mξij,(i=1,2,...,n.j=1,2,...,m)
注:这里是默认各个指标重要程度相同的情况,当不同是可按其他方式加权。
(5)分析结果,关联度大的越好。
三. Topsis(理想解法)
1.理想解法原理
设多属性的方案决策集 D = { d 1 , d 2 , . . . , d m } D=\{d_{1},d_{2},...,d_{m}\} D={d1,d2,...,dm},衡量一个方案优劣的属性变量为 x 1 , x 2 , . . . , x n x_{1},x_{2},...,x_{n} x1,x2,...,xn.对于方案集中的某方案 d i d_{i} di对应的属性值构成的向量 ( a i 1 , a i 2 , . . . , a i n ) (a_{i1},a_{i2},...,a_{in}) (ai1,ai2,...,ain)唯一确定了 n n n维空间的一个点,这个点可以唯一地表征方案 d i d_{i} di.选取正理想解(各个属性最大值构成的向量) C 1 = ( m a x ( a i 1 ) , m a x ( a i 2 ) , . . . , m a x ( a i n ) ) C1=(max(a_{i1}),max(a_{i2}),...,max(a_{in})) C1=(max(ai1),max(ai2),...,max(ain)),负理想解(各个属性最小值构成的向量) C 2 = ( m i n ( a i 1 ) , m i n ( a i 2 ) , . . . , m i n ( a i n ) ) C2=(min(a_{i1}),min(a_{i2}),...,min(a_{in})) C2=(min(ai1),min(ai2),...,min(ain)).对于空间中离正理想解近离负理想解远的 d i d_{i} di确定的点对应的方案更优。
2.Topsis法步骤
(1)对属性值矩阵
b
i
j
bij
bij做一致化,无量纲处理。
(2)确定各个属性权重向量
W
=
(
w
1
,
w
2
,
.
.
.
,
w
n
)
W=(w_{1},w_{2},...,w_{n})
W=(w1,w2,...,wn),对属性值矩阵加权得到加权后的属性值矩阵
c
i
j
,
i
=
1
,
2...
,
m
.
j
=
1
,
2
,
.
.
.
,
n
c_{ij},i=1,2...,m.j=1,2,...,n
cij,i=1,2...,m.j=1,2,...,n。
(3)确定正理想解
C
1
C1
C1和负理想解
C
2
C2
C2。
(4)计算各个方案
d
i
d_{i}
di对应的属性值向量到正理想解的距离
s
i
+
s_{i}^+
si+和到负的理想解的距离
s
i
−
s_{i}^-
si−。计算公式如下:
s
i
+
=
∑
j
=
1
n
(
a
i
j
−
m
a
x
(
a
i
j
)
)
2
,
i
=
1
,
2
,
.
.
.
,
m
s_{i}^{+}=\sqrt{\sum_{j=1}^{n} (a_{ij}-max(a_{ij}))^{2}},i=1,2,...,m
si+=j=1∑n(aij−max(aij))2
,i=1,2,...,m
s
i
−
=
∑
j
=
1
n
(
a
i
j
−
m
i
n
(
a
i
j
)
)
2
,
i
=
1
,
2
,
.
.
.
,
m
s_{i}^{-}=\sqrt{\sum_{j=1}^{n} (a_{ij}-min(a_{ij}))^{2}},i=1,2,...,m
si−=j=1∑n(aij−min(aij))2
,i=1,2,...,m
(5)将上两式综合可以得到
f
i
f_{i}
fi用于综合衡量方案
d
i
d_{i}
di到正负理想解的距离。
f
i
f_{i}
fi越大那么这个方案就越优秀。
f
i
=
s
i
−
s
i
−
+
s
i
+
,
i
=
1
,
2
,
.
.
.
,
m
f_{i}=\frac{s_{i}^{-}}{s_{i}^{-}+s_{i}^{+}},i=1,2,...,m
fi=si−+si+si−,i=1,2,...,m
四.线性加权综合评价模型(不是很推荐用)
线性加权综合评价模型是一种常用的多指标决策方法,它将各个指标的权重与指标值线性组合起来,得到一个综合评价值,用于评价被评价对象的综合表现。其基本思想是:将各个评价指标的重要性(权重)通过权重系数进行量化,然后将各个指标的值按照这些权重进行加权,得到一个综合评价值。这个综合评价值可以用于对被评价对象进行排名或分类。
线性加权综合评价模型的数学表达式如下:
S
=
w
1
x
1
+
w
2
x
2
+
.
.
.
+
w
n
x
n
S = w1x1 + w2x2 + ... + wnxn
S=w1x1+w2x2+...+wnxn
其中,S表示综合评价值,w1, w2, …, wn表示各个评价指标的权重,x1, x2, …, xn表示各个评价指标的取值。
线性加权综合评价模型的优点是简单易操作,计算方便,可以对各个指标的重要性进行量化,并将其考虑在评价中。同时,该模型还可以进行灵活的权重调整,以适应不同的评价需求。
但是,线性加权综合评价模型也存在一些缺点。首先,权重的确定比较主观,不同的评价者可能会给出不同的权重值。其次,该模型假设不同指标的影响是相互独立的,但实际上各指标之间可能存在一定的相关性,这种相关性可能会影响到评价结果的准确性。因此,在使用线性加权综合评价模型时,需要注意权重的确定和指标之间的关系,以保证评价结果的可靠性。
五.熵值法
1.熵值法原理
熵值法是一种常用的多指标决策方法,适用于评价对象的指标比较多、指标之间相互独立、难以确定权重的情况。其基本思想是:将各个指标的取值标准化,然后计算每个指标的熵值和权重,最后将各个指标的熵值和权重进行加权求和,得到一个综合评价值。其核心原理是信息熵的概念,即信息越不确定,熵值越大,反之熵值越小,通过计算各个指标的熵值来确定其对综合评价的贡献程度,从而得到各指标的权重。(要是学过决策树算法,这里的思想应该很好理解,不再赘述)
2.熵值法步骤
(1)收集数据:收集所有需要评价的指标数据,并将其转化为具体的数值形式。
(2)数据标准化:将各个指标的取值范围标准化,使得不同指标之间具有可比性。常用的方法有线性标准化、对数标准化和正态标准化等。
(3)计算熵值:根据信息熵的概念,计算每个指标的熵值。熵值越小,指标贡献越大。计算公式为:
E
i
=
−
1
ln
n
∑
j
=
1
n
x
i
j
∑
k
=
1
n
x
k
j
ln
x
i
j
∑
k
=
1
n
x
k
j
E_i=-\frac{1}{\ln n}\sum_{j=1}^n \frac{x_{ij}}{\sum_{k=1}^n x_{kj}}\ln\frac{x_{ij}}{\sum_{k=1}^n x_{kj}}
Ei=−lnn1j=1∑n∑k=1nxkjxijln∑k=1nxkjxij,其中
n
n
n为指标个数,
x
i
j
x_{ij}
xij表示第
i
i
i个指标的第
j
j
j个样本值。
(4)计算权重:根据熵值计算每个指标的权重,即其对综合评价结果的贡献程度。计算公式为:
w
i
=
1
−
E
i
n
−
∑
j
=
1
n
E
j
w_i=\frac{1-E_i}{n-\sum_{j=1}^n E_j}
wi=n−∑j=1nEj1−Ei。
解释一下这一步:(1-熵值
E
i
E_{i}
Ei)越大说明信息的差异性越大,可以理解如果一个指标下样本的差异性较大,那么这个指标对综合评价的影响更大。举个简单的例子,小明班上进行了一次考试,大家语文都只考了80多分,但是数学成绩从0-100分都有人,那么对小明班级这次考试成绩排名影响更大的就是数学成绩,而不是语文成绩。
(5)综合评价:将各个指标的熵值和权重进行加权求和,得到一个综合评价值。计算公式为:
S
=
∑
i
=
1
n
w
i
x
i
S=\sum_{i=1}^n w_i x_i
S=∑i=1nwixi,其中
x
i
x_i
xi为第
i
i
i个指标的标准化值。
六.秩和比法
1.秩和比法的编秩步骤的秩和矩阵中的秩什么关系
编秩中的秩和矩阵中的秩是两个不同的概念,它们之间没有直接的关系。在编秩中,秩是指将一组数据按大小排序后,为每个数据分配的一个排名或序号。编秩的目的是用秩次代替原始数据,使数据不再受到极端值和异常值的影响,方便进行统计分析。秩的大小反映了数据在整个数据集中所处的位置,可以用于计算秩和、秩平均数、秩差等统计特征。而在矩阵中,秩是指矩阵中非零行的个数。它是矩阵的一个重要特征,可以用于判断矩阵是否可逆、求解线性方程组、计算特征值和特征向量等。虽然编秩中的秩和矩阵中的秩不是同一个概念,但它们都有一个共同的特点,即都可以用来描述数据或矩阵的某种特征。
2.秩和比法的原理
秩和比法是一种基于秩次的非参数统计方法,用于比较两个或多个独立样本组之间的差异。它的原理是将每个样本组内的观测值按大小排列,并赋予它们相应的秩次,然后比较每个样本组的秩和大小,以判断它们之间的差异是否显著。
3.为什么秩和比越大评价结果越高
在编秩的过程我们是主动的去为更优的数据编排更大的秩的,比如极小型指标从小到大编秩,极大型指标从大到小编秩。于是更优的指标值总是有更大的秩次,于是最后秩和比大的样本就更加优秀。
4.秩和比法的步骤
(1)对数据矩阵
A
m
,
n
A_{m,n}
Am,n(m是样本量,n是特征量)编秩,极小型指标从小到大编秩,极大型指标从大到小编秩。得到秩矩阵
R
R
R.
(2)计算秩和比,公式如下:
R
S
R
i
=
1
m
∑
j
=
1
n
w
j
R
i
j
RSR_{i}=\frac{1}{m}\sum_{j=1}^{n}w_{j}R_{ij}
RSRi=m1j=1∑nwjRij,
w
j
w_{j}
wj是指标
j
j
j的权重。
(3)秩和比大的评价越好
七.总结模型优缺点与选用策略
- Topsis
- 优点:简单易用,适用于多指标综合评价问题,能够考虑指标的权重和正负效应,结果易于解释。
- 缺点:对指标的标准化方法较为敏感,需要选取合适的标准化方法,同时假设各指标之间的权重是固定的,可能会忽略一些重要的因素。
- 适用情形:适用于多指标综合评价问题,特别是在需要考虑指标权重和正负效应的情况下。
- 模糊综合评价法
- 优点:能够处理模糊和不确定信息,能够反映评价对象的整体水平,适用于多指标综合评价问题。
- 缺点:需要确定模糊隶属度函数和权重,这些参数的确定会影响评价结果的准确性。
- 适用情形:适用于处理模糊和不确定信息的多指标综合评价问题。
- 灰色关联分析模型
- 优点:能够处理样本数据不完整、不确定的情况,适用于样本数据较少的情况,结果易于解释。
- 缺点:对于样本数据较多、相差较大的情况,结果可能会失真,同时需要确定关联度函数和权重等参数。
- 适用情形:适用于样本数据不完整、不确定的情况,特别是在数据较少的情况下。
- 熵值法
- 优点:能够考虑指标之间的相对重要性,适用于多指标综合评价问题。
- 缺点:对指标数据的标准化方法较为敏感,需要选取合适的标准化方法,同时需要确定权重。
- 适用情形:适用于多指标综合评价问题,特别是需要考虑指标之间的相对重要性的情况下。
- 秩和比法
- 优点:不需要对数据做过多的假设,适用于非正态分布或存在异常值的情况,结果易于解释。
- 缺点:适用范围较窄,只能用于比较两个或多个独立样本组之间的差异。
- 适用情形:适用于比较两个或多个独立样本组之间的差异,特别是在数据分布非正态或存在异常值的情况下。


