c++判断三维中一个点是否在任意位置的长方体中_判断点是否落在一个长方体中

如题 这种长方体可以在三维空间中任意旋转

这个是当时参考的原理 https://blog.csdn.net/hit1524468/article/details/79857665
以下代码是这种思路的实现 不想看的话可以直接使用

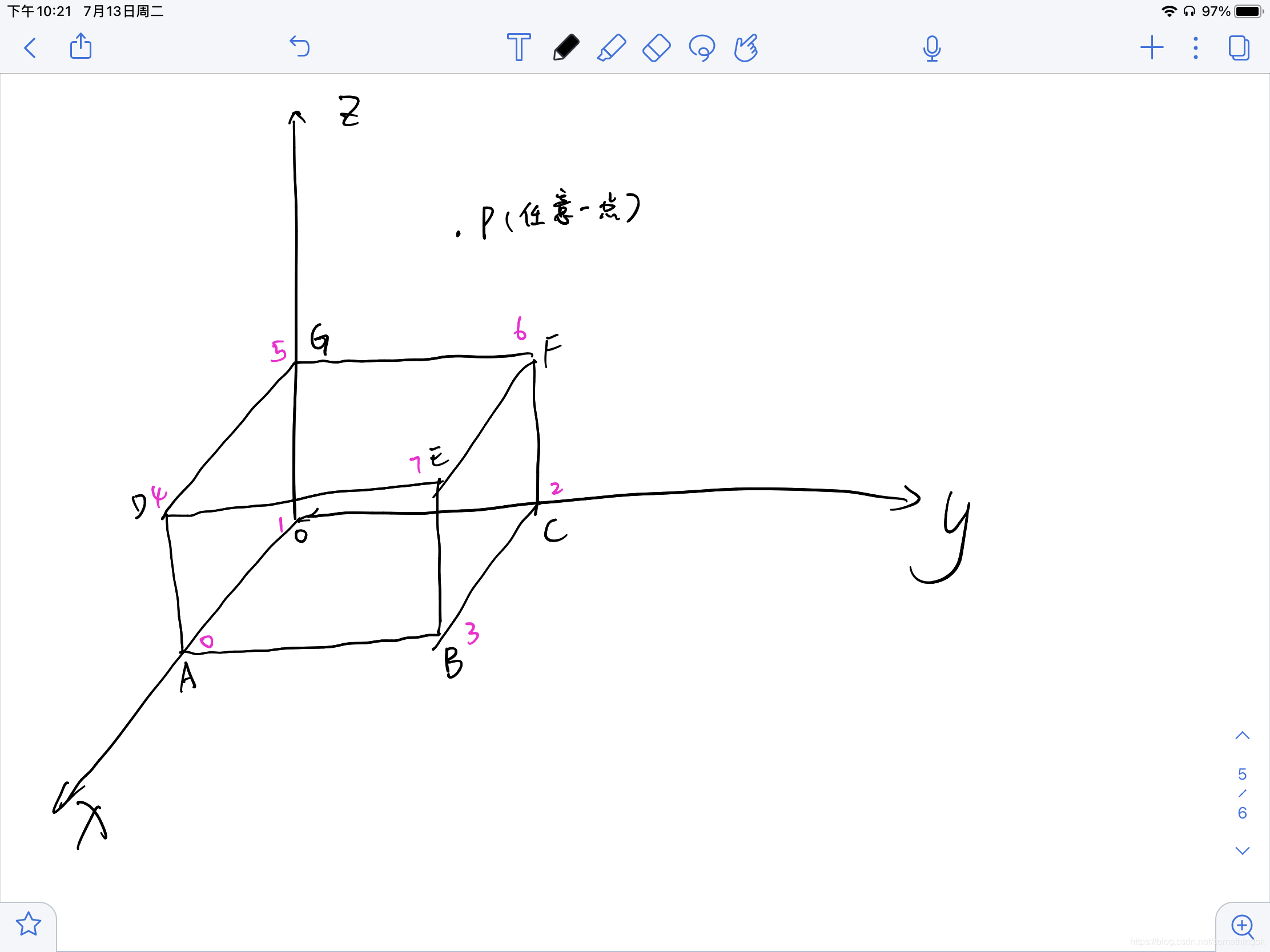
要使用的话必须按照一定的规则来使用，如下图

p点为你要判断的是否在块体中的点，这里注意块体的8个点的顺序。我是用自定义结构XYZ的数组来存储这8个点的，顺序一定不能错。按照图中粉色字顺序放入数组。比如cuboid[0]的x，y，z坐标一定是对应A的这个点，如果这个块体是旋转的，不是按图中这样规则的摆放，你可以自己设定[0]对应的点，但是这个点确定后，要按图中的顺序继续放入。得到这样的数组后，和要判断的点一起传入函数即可，返回true代表点在块体内，返回false代表点不在块体内。如果点在块体的边界上，也算不在块体内，如果想算在块体内需要把最后if判断的所有的<0改为<=。

typedef struct {	// 点的结构定义
  double x,y,z;
} XYZ;
bool pointIsInsideCuboid( XYZ p,XYZ* cuboid )
{
	//首先判断点是否在左右两面的中间 此时法线为y轴
	XYZ vector_DP;
	XYZ vector_EP; 
	XYZ vector_DE;//法线y
	//计算向量DE
	vector_DE.x=cuboid[7].x-cuboid[4].x;vector_DE.y=cuboid[7].y-cuboid[4].y;vector_DE.z=cuboid[7].z-cuboid[4].z;
	//计算向量DP
	vector_DP.x=p.x-cuboid[4].x;vector_DP.y=p.y-cuboid[4].y;vector_DP.z=p.z-cuboid[4].z;
	//计算向量EP
	vector_EP.x=p.x-cuboid[7].x;vector_EP.y=p.y-cuboid[7].y;vector_EP.z=p.z-cuboid[7].z;
	//计算向量点乘的结果
	//DP点乘DE
	double DP_DE;
	DP_DE=vector_DP.x*vector_DE.x+vector_DP.y*vector_DE.y+vector_DP.z*vector_DE.z;
	//EP点乘DE
	double EP_DE;
	EP_DE=vector_EP.x*vector_DE.x+vector_EP.y*vector_DE.y+vector_EP.z*vector_DE.z;

	//然后判断点是否在上下两面的中间 此时法线为z轴
	/*XYZ vector_DP;*/ //DP已经存在了 直接用上面的
	XYZ vector_AP; 
	XYZ vector_AD;//法线y
	//计算向量AP
	vector_AP.x=p.x-cuboid[0].x;vector_AP.y=p.y-cuboid[0].y;vector_AP.z=p.z-cuboid[0].z;
	//计算向量AD
	vector_AD.x=cuboid[4].x-cuboid[0].x;vector_AD.y=cuboid[4].y-cuboid[0].y;vector_AD.z=cuboid[4].z-cuboid[0].z;
	//计算向量点乘的结果
	//AD AP
	double AD_AP;
	AD_AP=vector_AD.x*vector_AP.x+vector_AD.y*vector_AP.y+ vector_AD.z*vector_AP.z;
	//AD DP
	double AD_DP;
	AD_DP=vector_AD.x*vector_DP.x+vector_AD.y*vector_DP.y+ vector_AD.z*vector_DP.z;

	//最后判断点是否在前后两面的中间 此时法线为x轴 
	XYZ vector_OA;//法线
	XYZ vector_OP;
	/*XYZ vector_AP;*/ //已有
	vector_OA.x=cuboid[0].x;vector_OA.y=cuboid[0].y;vector_OA.z=cuboid[0].z;
	vector_OP.x=p.x;vector_OP.y=p.y;vector_OP.z=p.z;
	//计算向量点乘的结果
	//OP OA
	double OP_OA;
	OP_OA=vector_OP.x*vector_OA.x+vector_OP.y*vector_OA.y+vector_OP.z*vector_OA.z;
	//AP OA 
	double AP_OA;
	AP_OA=vector_AP.x*vector_OA.x+vector_AP.y*vector_OA.y+vector_AP.z*vector_OA.z;

	if (DP_DE*EP_DE<0&&AD_AP*AD_DP<0&&OP_OA*AP_OA<0)
	{
		return true;
	}else
	{
		return false;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61