- 1OpenCV-python图像处理(包含OpenCV库安装)_清华源安装opencv
- 2计网 数据链路层_交换机polling
- 3react18+antd5从0到1的后台管理系统(一)_react18开发管理后台
- 4钉钉在线求饶?爬取钉钉App Store真实评价数据并分析
- 5idea回滚以及码云仓库回滚
- 6左神算法学习日记——单调栈_单调栈 左神模版
- 7浏览器安全_xss 攻击是不是关闭浏览器就会断开
- 8MacOS 下载 brew_brew下载
- 9Python多种方式实现”欢迎小红“_print("你好\nhello") print("你好\\hello") print('小红说:"
- 1014个适合后台管理系统快速开发的前端框架_后台管理框架
数据结构——优先级队列(堆)
赞
踩
目录
一、优先级队列是什么?
- 优先级队列是一种特殊的队列,它的每个元素都有一个优先级。当出队操作时,队列会按照元素优先级的高低顺序从队列中取出一个元素并删除。具有相同优先级的元素则按照它们在队列中的顺序排列。
- 优先级队列常用于任务调度、事件处理等场景。它可以确保优先级高的任务或事件先被处理,从而提高系统的响应速度和效率。在实现优先级队列时,常使用堆(如二叉堆或斐波那契堆)等数据结构来实现,以保证高效的插入和删除操作。
二、优先级队列的模拟实现
1. 堆的概念
满足任意结点的值都大于其子树中结点的值,叫做大根堆,或者最大堆;反之,则是小根堆,或者最小堆。当一个堆为大堆时,它的每一棵子树都是大堆。当一个堆为小堆时,它的每一棵子树都是小堆。
堆的性质
- 堆中某个节点的值总是不大于或不小于其父节点的值;(也就是有小大根堆之分)
- 堆总是一棵完全二叉树。
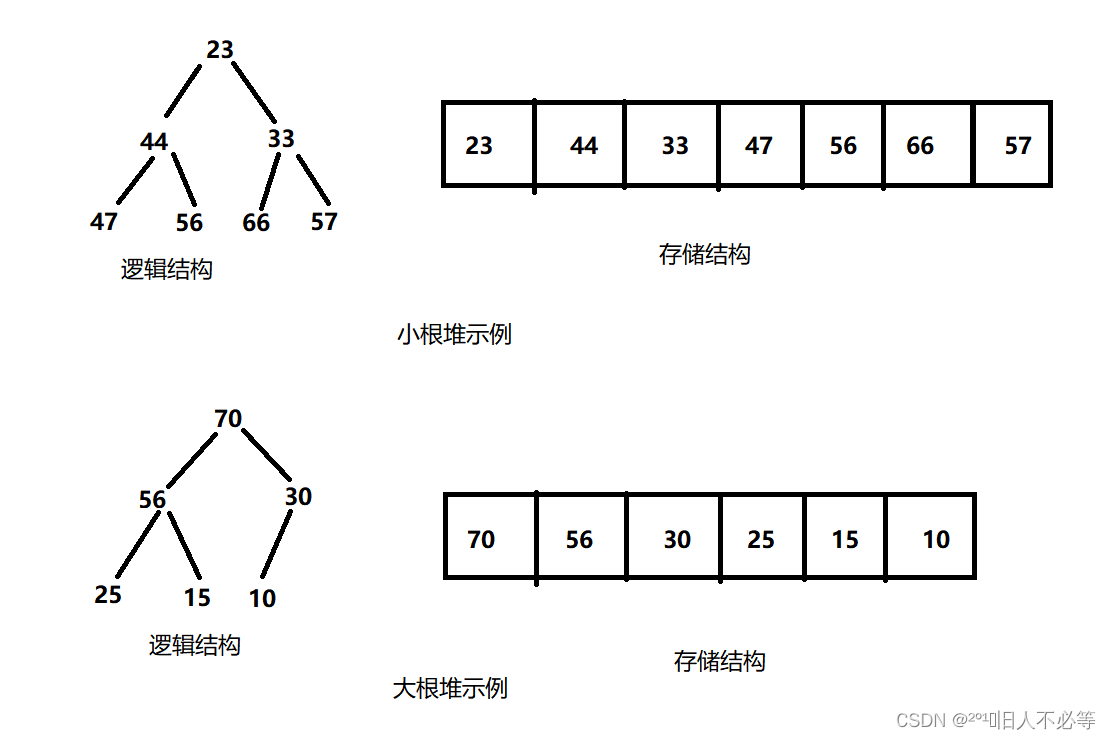
2. 堆的存储方式
堆是一棵完全二叉树,因此可以层序的规则采用顺序的方式来高效存储
注意:对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率比较低。
也就是说:
完全二叉树适合使用数组进行存储,层序遍历; 一般二叉树不适合顺序方式进行存储,浪费存储空节点的空间。
根据二叉树的性质 我们假设i为节点在数组中的下标 则有
- 如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2
- 如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子
- 如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子
3. 堆的创建
创建堆只有两种堆可以创建,要不就是大根堆,要不就是小根堆。而要满足大根堆还是小根堆的逻辑,就要向下调整的操作才能实现。要想自己实现堆,堆本身就是一个数组,因此创建一个数组来创建堆。
对于集合 { 28,16,10,19,29,35,66,50,26,38 } 中的数据,如果将其创建成堆呢?
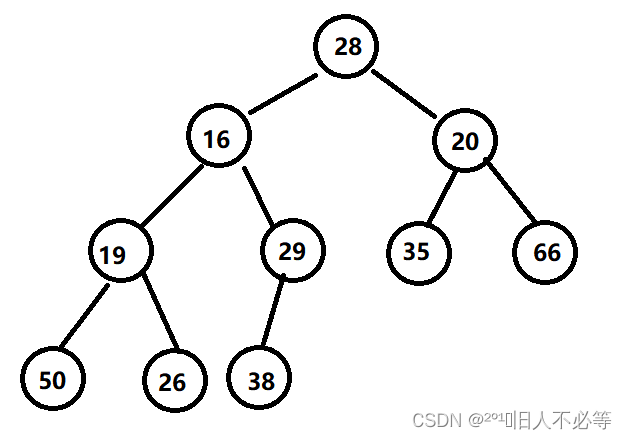
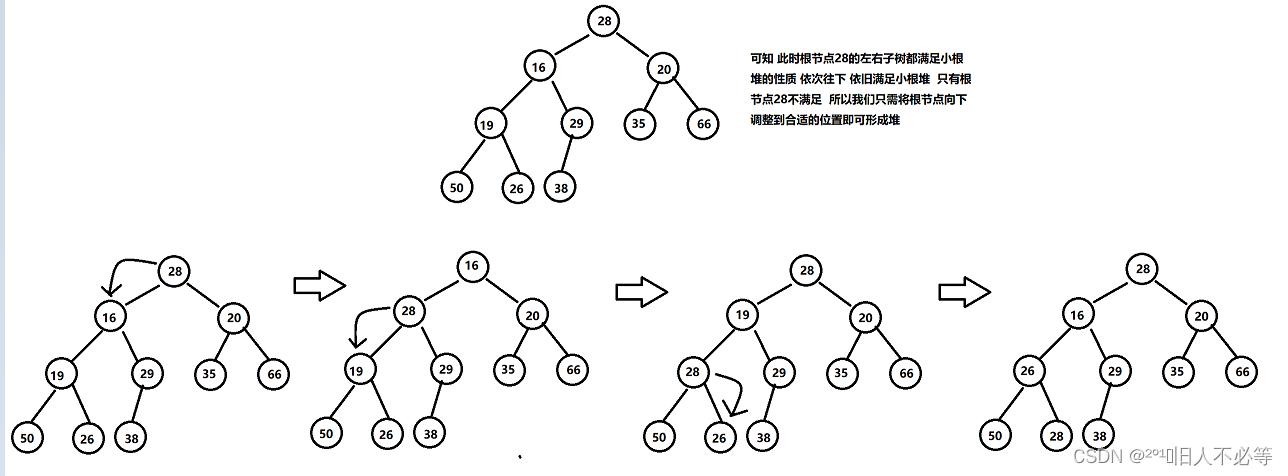
仔细观察上图后发现:根节点的左右子树已经完全满足堆的性质,因此只需将根节点向下调整好即可。
1.向下过程(以小根堆为例):
1. 让 parent 标记需要调整的节点,child 标记 parent 的左孩子(注意:parent 如果有孩子一定先是有左孩子)
2. 如果 parent 的左孩子存在,即: child < size, 进行以下操作,直到 parent 的左孩子不存在:
- 看 parent 右孩子是否存在,存在找到左右孩子中最小的孩子,让 child 进行标记
- 将 parent 与较小的孩子 child 比较,如果:parent 小于较小的孩子 child,调整结束;
- 否则:交换 parent 与较小的孩子 child,交换完成之后,parent 中大的元素向下移动,可能导致子树不满足对的性质,因此需要继续向下调整,即 parent = child; child = parent*2+1;然后继续重复操作。
- private void shiftDown(int parent , int len){
- // child先标记parent的左孩子,因为parent可能有左孩子没有右孩子
- int child = 2*parent+1;
- while (child<len){
- // 如果右孩子存在,找到左右孩子中较小的孩子,用child进行标记
- if (child+1<len && elem[child] > elem[child+1]){
- child++;
- }
- // 将双亲与较小的孩子交换
- if (elem[child] > elem[parent]){
- int tmp = elem[child];
- elem[child] = elem[parent];
- elem[parent] = tmp;
- // parent中大的元素往下移动,可能会造成子树不满足堆的性质,因此需要继续向下调整
- parent=child;
- child = 2*parent+1;
- }else {// 如果双亲比其最小的孩子还小,说明该结构已经满足堆的特性了
- break;
- }
- }
- }

注意:在调整以parent为根的二叉树时,必须要满足parent的左子树和右子树已经是堆了才可以向下调整。
时间复杂度分析:最坏的情况即图示的情况,从根一路比较到叶子,比较的次数为完全二叉树的高度,即时间复杂度为O(logN)
2. 建堆
- public void createHeap(){
- // 找倒数第一个非叶子节点,从该节点位置开始往前一直到根节点,遇到一个节点,应用向下调整
- for (int parent = (usedSize-1-1)/2; parent >=0; parent--) {
- shiftDown(parent,usedSize);
- }
- }
3. 堆的插入与删除
1. 堆的插入
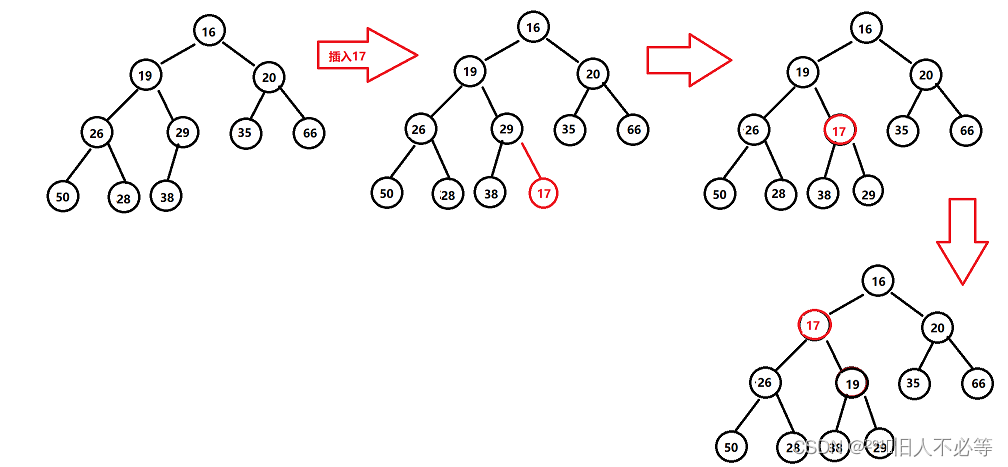
插入之后仍然要保证原来的大根堆(小根堆)不变:
先插入到最后一棵子树的空的孩子结点处(考虑是否需要扩容),然后该节点直接与根结点进行比较,根据大小堆关系必要时互换,一旦产生互换就进行现在根节点与孩子节点的变换,不断重复,直至到达根结点。
注意每次交换父亲节点与孩子节点值后后,child和parent都要发生变化!!
什么时候停止循环:child==0 or parent<0
注意:插入是插入到最后,然后再慢慢进行【向上调整】!
- public void offer(int val){
- if(isFull()){
- elem = Arrays.copyOf(elem,2*elem.length);
- }
- elem[usedSize++] = val;
-
- shiftUp(usedSize-1);
- }
- public void shiftUp(int child){
-
- int parent = (child-1)/2;
-
- while (child>0){
-
- if (elem[child]>elem[parent]){
- swap(elem , child,parent);
- child = parent;
- parent = (child-1)/2;
- }else {
- break;
- }
- }
- }
2. 堆的删除
删除(出队):出的是优先级最高的元素;即:优先级队列的删除只能删除堆顶的元素。
堆顶元素与最后一个元素进行交换,然后usedSize就–(此时队列中有效长度范围内就不包含已经交换至最后的堆顶元素了)
此时只需要【向下调整】0下标开始的子树即可。
- public void pop(){
- if (isEmpty()){
- return;
- }
- swap(elem,0,usedSize-1);
- usedSize--;
- shiftDown(0,usedSize);
- }
三、常见接口介绍
| 构造器 | 功能介绍 |
| PriorityQueue() | 创建一个空的优先级队列,默认容量是11 |
| PriorityQueue(int initialCapacity) | 创建一个初始容量为initialCapacity的优先级队列,注意: initialCapacity不能小于1,否则会抛IllegalArgumentException异 常 |
| PriorityQueue(Collection<? extends E> c) | 用一个集合来创建优先级队列 |
- static void TestPriorityQueue(){
- // 创建一个空的优先级队列,底层默认容量是11
- PriorityQueue<Integer> q1 = new PriorityQueue<>();
- // 创建一个空的优先级队列,底层的容量为initialCapacity
- PriorityQueue<Integer> q2 = new PriorityQueue<>(100);
- ArrayList<Integer> list = new ArrayList<>();
- list.add(4);
- list.add(3);
- list.add(2);
- list.add(1);
- // 用ArrayList对象来构造一个优先级队列的对象
- // q3中已经包含了三个元素
- PriorityQueue<Integer> q3 = new PriorityQueue<>(list);
- System.out.println(q3.size());
- System.out.println(q3.peek());
- }

注意:默认情况下,PriorityQueue队列是小堆,如果需要大堆需要用户提供比较器
- // 用户自己定义的比较器:直接实现Comparator接口,然后重写该接口中的compare方法即可
- class IntCmp implements Comparator<Integer>{
- @Override
- public int compare(Integer o1, Integer o2) {
- return o2-o1;
- }
- }
注意事项:
- java的优先级队列底层数组默认大小是11
- 当对优先级队列指定大小的时候,不要给<=0的容量,一定要>1,否则会抛出异常。
- 比较器Comparator是需要自己传入的,不传入就会默认这个变量是可比较的;默认实现的是Comparable接口。
- 当使用比较器Comparator的对象作为参数传入时,不管走的哪个方法,数组的容量都是被赋予的。
- offer是如何维护的?如何保证小根堆的呢?其实就是在重写compare方法(Compara比较器)时,如果o1-o2就是默认的小堆,o2-o1则是大堆;因为一旦两个相减<0就进行就进行交换。(o1就是当前传入的对象!!)
四. 堆的应用
1. 堆排序(从小到大排)
一个数组根据从小到大排序,要创建大堆来排;一个数组根据从大到小排序,要创建小堆来排。此处就以创建大堆为例。首先将堆顶的元素和堆中的最后一个元素交换,交换后再向下调整,调整后再与堆的倒数第二个元素进行交换。
- public void HeapSort() {
- int end = usedSize-1;
- while(end>0) {
- int tmp = elem[0];
- elem[0] = elem[end];
- elem[end] = tmp;
- shiftUp(0,end);
- end--;
- }
- }
2.top--K问题
top-k应用:求前k个最大(建小根堆)/最小、求第k大(建小根堆–堆顶元素)/小。
top-k问题:
假设:100个数据中,找前k个最大(最小)
方法一:将数据放入大根堆(小根堆)中–堆顶元素就是max(min),然后出k次–每出一次都会进行调整成大小根堆
(注意在建优先级队列时直接传入比较器Comparator)和重写compare方法)
缺陷:如果堆较大的话,时间复杂度会较高:O(N*log2N)
优化方法:如果是找前k个最大的
先建立一个k大小的小根堆(注意是小根堆)来存储数组的前k个元素,然后从k下标开始依次遍历,与堆顶元素进行比较,如果堆顶元素<当前元素,那么堆顶元素一定不是所要找的前k个最大之一,所以将堆顶元素进行出堆poll(堆顶元素与最后一个元素互换),然后调整成小根堆,再将当前元素放置最后一个元素位置,再调整小根堆offer。循环遍历。
时间复杂度:O(N*log2K) (N是结点个数,K是前K个)
代码:(以 找前k个最大值为例)
- class Inim implements Comparator<Integer>{
-
- @Override
- public int compare(Integer o1, Integer o2) {
- return o2.compareTo(o1);
- }
- }
-
- class Solution {
- public int[] smallestK(int[] arr, int k) {
- int[] tmp = new int[k];
-
- if(arr== null || k==0){
- return tmp;
- }
- Inim inim = new Inim();
- Queue<Integer> minHeap = new PriorityQueue<>(inim);
-
- //遍历数组的前k个 放到堆当中
- for (int i = 0; i < k; i++) {
- minHeap.offer(arr[i]);
- }
- //遍历剩下的k-1个 每次和堆顶元素进行比较
-
- for (int i = k; i < arr.length; i++) {
- if (minHeap.peek() > arr[i]){
- minHeap.poll();
- minHeap.offer(arr[i]);
- }
- }
- for (int i = 0; i < k ; i++) {
- tmp[i] = minHeap.poll();
- }
- return tmp;
- }
- }

五、用堆模拟实现优先级队列(完整代码)
- import java.util.Arrays;
-
- public class TestHeap {
- public int[] elem;
- public int usedSize;
-
- public TestHeap() {
- this.elem = new int[10];
- }
-
- public void initElem(int[] array){
- for (int i = 0; i < array.length; i++) {
- elem[i] = array[i];
- usedSize++;
- }
- }
- public void createHeap(){
- // 找倒数第一个非叶子节点,从该节点位置开始往前一直到根节点,遇到一个节点,应用向下调整
- for (int parent = (usedSize-1-1)/2; parent >=0; parent--) {
- shiftDown(parent,usedSize);
- }
- }
-
- //parent 父亲节点下标
- //len 每棵树结束下标
- //向下调整时间复杂度是N
- private void shiftDown(int parent , int len){
- // child先标记parent的左孩子,因为parent可能有左孩子没有右孩子
- int child = 2*parent+1;
- while (child<len){
- // 如果右孩子存在,找到左右孩子中较小的孩子,用child进行标记
- if (child+1<len && elem[child] < elem[child+1]){
- child++;
- }
- // 将双亲与较小的孩子交换
- if (elem[child] > elem[parent]){
- int tmp = elem[child];
- elem[child] = elem[parent];
- elem[parent] = tmp;
- // parent中大的元素往下移动,可能会造成子树不满足堆的性质,因此需要继续向下调整
- parent=child;
- child = 2*parent+1;
- }else {// 如果双亲比其最小的孩子还小,说明该结构已经满足堆的特性了
- break;
- }
- }
- }
-
- public void shiftUp(int child){
-
- int parent = (child-1)/2;
-
- while (child>0){
-
- if (elem[child]>elem[parent]){
- swap(elem , child,parent);
- child = parent;
- parent = (child-1)/2;
- }else {
- break;
- }
- }
- }
- //向上调整的时间复杂度为N*logN
- public void offer(int val){
- if(isFull()){
- elem = Arrays.copyOf(elem,2*elem.length);
- }
- elem[usedSize++] = val;
-
- shiftUp(usedSize-1);
- }
-
- public boolean isFull(){
- return usedSize == elem.length;
- }
-
- public void pop(){
- if (isEmpty()){
- return;
- }
- swap(elem,0,usedSize-1);
- usedSize--;
- shiftDown(0,usedSize);
- }
-
- public boolean isEmpty(){
- return usedSize == 0;
- }
-
- public void swap(int[] array ,int i ,int j){
- int tmp = elem[i];
- elem[i] = elem[j];
- elem[j] = tmp;
- }
-
-
- }



