算法--单词接龙(BFS)_算法单词接龙

字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列：

序列中第一个单词是 beginWord 。
序列中最后一个单词是 endWord 。
每次转换只能改变一个字母。
转换过程中的中间单词必须是字典 wordList 中的单词。
给你两个单词 beginWord 和 endWord 和一个字典 wordList ，找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0。

https://leetcode-cn.com/problems/word-ladder/

最短转换序列长度--广度优先搜索

1.广度优先搜索

把每个单词都抽象为一个点，如果两个单词可以只改变一个字母进行转换，那么说明他们之间有一条双向边。因此我们只需要把满足转换条件的点相连，就形成了一张图。

以 beginWord 为图的起点，以 endWord 为终点进行广度优先搜索，寻找 beginWord 到 endWord 的最短路径。

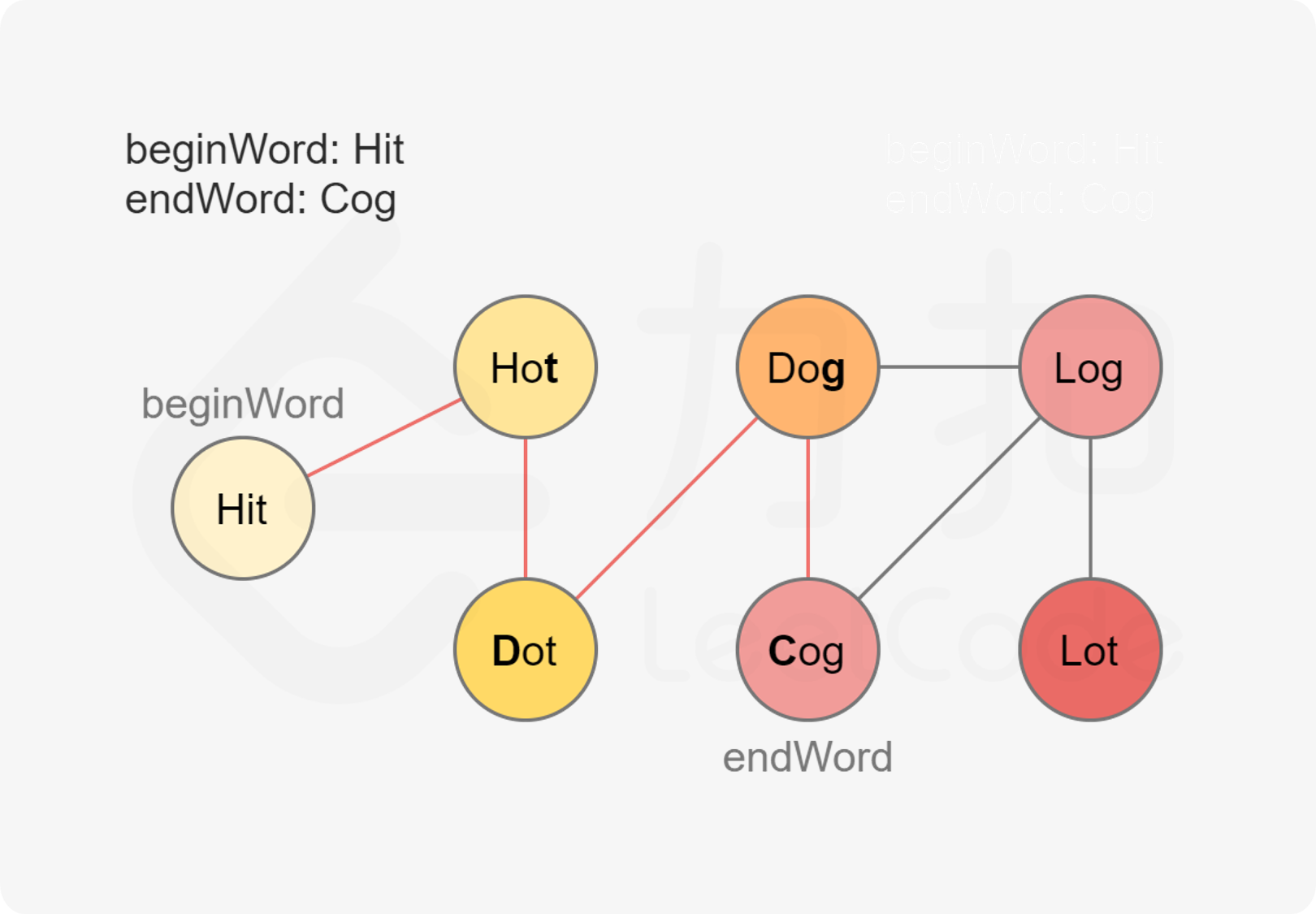
将给定单词集合和开始节点构建一张图，从开始节点到指定结束节点搜索最短路径。

利用哈希表来存储单词和单词编号的关系

利用List<List<Integer>>列表来存储每个单词与其相邻单词的关系，理论上只有当两个单词只有一个字母不同时，在图中会存在一条边，这里为了便于简化单词边关系的判断逻辑，增加一些虚拟节点，从每个单词触发，依次仅改变每一个字母来得到一个当前单词的相邻单词集合，变为该单词的边关系。

// 保存单词和编号的关系
    Map<String, Integer> wordId = new HashMap<>();
    // 保存单词与相邻节点的关系
    List<List<Integer>> edge = new ArrayList<>();
    // 单词数量计数
    int nodeNum = 0;
 
 
    public void addWord(String word) {
        if (!wordId.containsKey(word)) {
            wordId.put(word, nodeNum++);
            edge.add(new ArrayList<>());
        }
    }
 
    public void addEdge(String word) {
        addWord(word);
        int id1 = wordId.get(word);
        char[] array = word.toCharArray();
        for (int i=0; i<array.length; i++) {
            char tmp = array[i];
            array[i] = '*';
            String newWord = new String(array);
            addWord(newWord);
            int id2 = wordId.get(newWord);
            edge.get(id1).add(id2);
            edge.get(id2).add(id1);
            array[i] = tmp;
        }
    }
 
 
    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        // 将所有单词添加进图中
        wordList.forEach(this::addEdge);
        // 将开始单词添加进图中
        addEdge(beginWord);
        if (!wordId.containsKey(endWord)) return 0;
        int[] dis = new int[nodeNum];
        Arrays.fill(dis, Integer.MAX_VALUE);
        int beginId = wordId.get(beginWord);
        int endId = wordId.get(endWord);
        // 记录从单词i开始到达结束单词的路径 起始单词初始化为0 其余初始化为最大值
        dis[beginId] = 0;
        Queue<Integer> queue = new LinkedList<>();
        // 从开始单词开始搜索
        queue.add(beginId);
        while (!queue.isEmpty()) {
            int x = queue.poll();
            // 如果当前单词等于结束单词 已经找到 返回
            if (x == endId) return dis[endId] / 2 + 1;
            // 否则 找出该单词所有可能到达的路径
            for (int it: edge.get(x)) {
                // 如果等于最大值 表示还没有遍历过
                if (dis[it] == Integer.MAX_VALUE) {
                    // 单词x到达结束单词路径为dis[x]
                    // 单词it比单词x距离大一
                    dis[it] = dis[x] + 1;
                    queue.add(it);
                }
            }
        }
        return 0;
    }

2.双向优先搜索

构建图关系之后，从开始节点和结束节点开始，依次BFS遍历寻找，如果开始和结束都遍历过同一个节点，则说明最短路径已经找到。

// 双向广度优先搜索
    public int ladderLength2(String beginWord, String endWord, List<String> wordList) {
        wordList.forEach(this::addEdge);
        addEdge(beginWord);
        if (!wordId.containsKey(endWord)) return 0;
 
        int[] disBegin = new int[nodeNum];
        Arrays.fill(disBegin, Integer.MAX_VALUE);
        int beginId = wordId.get(beginWord);
        disBegin[beginId] = 0;
        Queue<Integer> queBegin = new LinkedList<>();
        queBegin.add(beginId);
 
        int[] disEnd = new int[nodeNum];
        Arrays.fill(disEnd, Integer.MAX_VALUE);
        int endId = wordId.get(endWord);
        disEnd[endId] = 0;
        Queue<Integer> queEnd = new LinkedList<>();
        queEnd.add(endId);
 
        while (!queBegin.isEmpty() && !queEnd.isEmpty()) {
            // 从开始节点开始BFS
            int queBeginSize = queBegin.size();
            for (int i=0; i<queBeginSize; i++) {
                int nodeBegin = queBegin.poll();
                // 如果开始节点在结束队列中已经搜索过 则直接返回
                if (disEnd[nodeBegin] != Integer.MAX_VALUE) {
                    return (disBegin[nodeBegin] + disEnd[nodeBegin]) / 2 + 1;
                }
                // 遍历当前节点的所有相邻节点 更新距离
                for (int it: edge.get(nodeBegin)) {
                    if (disBegin[it] == Integer.MAX_VALUE) {
                        disBegin[it] = disBegin[nodeBegin] + 1;
                        queBegin.add(it);
                    }
                }
            }
 
            // 开始节点完成 尝试从结束节点开始BFS
            int queEndSize = queEnd.size();
            for (int i=0; i<queEndSize; i++) {
                int nodeEnd = queEnd.poll();
                // 如果结束节点在开始队列中已经搜索过 则直接返回
                if (disBegin[nodeEnd] != Integer.MAX_VALUE) {
                    return (disBegin[nodeEnd] + disEnd[nodeEnd]) / 2 + 1;
                }
                // 遍历当前节点的所有相邻节点 更新距离
                for (int it: edge.get(nodeEnd)) {
                    if (disEnd[it] == Integer.MAX_VALUE) {
                        disEnd[it] = disEnd[nodeEnd] + 1;
                        queEnd.add(it);
                    }
                }
            }
        }
        return 0;
    }

参考地址：https://leetcode-cn.com/problems/word-ladder/solution/dan-ci-jie-long-by-leetcode-solution/