- 1Unity 视频播放器,基于VideoPlayer,实现滑动进度条,显示视频时长,全屏显示,音量调节_unity 视频播放优化
- 2Docker容器绑定外部ip和端口_docker 容器ip映射到外面
- 3QT creator 最详细安装教程_qt creator安装
- 4Qt封装QPropertyAnimation动画基类,所有界面通用实现界面类似手机滑动切换_qparallelanimationgroup 页面平滑切换
- 5云计算1+X平台运维与开发认证(初级)操作题详解_1+x 云计算平台运维与开发认证(初级)实操部分
- 6【动态规划】【字符串】【行程码】1531. 压缩字符串
- 7(Windows下NVIDIA 显卡可用)ChatGLM-6B的安装文档(媲美GPT-3.5),存一个!_windows openmp安装
- 8itk中的黑白TopHat算法
- 9XUbuntu22.04之免费思维导图工具(二百零六)
- 10微信小程序根据步骤渲染数组中的不同内容_微信小程序渲染后端传过来的数组
人工智能学习——神经网络(matlab+python实现)_实现神经网络算法
赞
踩
人工智能学习——神经网络
前言
此文章仅作为个人学习笔记使用,主要介绍理论以及学习过程,仅供参考!
一、神经网络理论知识
1.人工神经网络的概念
人工神经网络(Artificial Neural Network,ANN),简称神经网络(Neural Network,NN)或类神经网络,是一种模仿生物神经网络的结构和功能的数学模型,用于对函数进行估计或近似。
2.神经元的概念
在生物神经网络中(见下图),每个神经元与其他神经元相连,当它“兴奋”时,就会向相连的神经元发送化学物质,从而改变这些神经元内的电位;如果某神经元的电位超过了一个“阈值”,那么它就会被激活,即“兴奋”起来,向其他神经元发送化学物质。 抑制状态同理,它具有时空整合的功能,具有很强的可塑性,人工神经元是由McCulloch 和 Pitts 将上述情形转化为典型的M-P 神经元模型。当我们把许多这样的神经元按一定的层次结构连接起来,就得到了神经网络。神经元是神经网络中的基础单元,相互连接,组成神经网络。
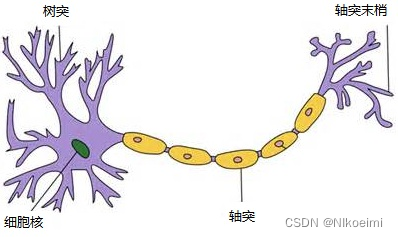
3.MP神经元模型
MP 神经元模型模型是人工神经元模型的基础。
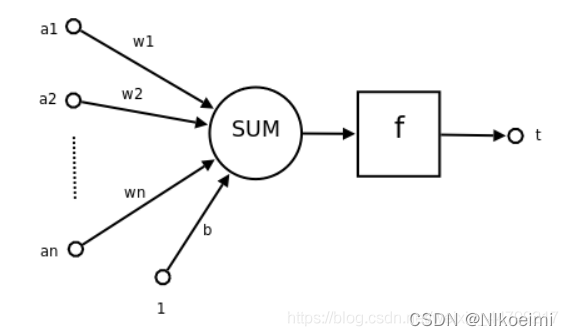
其中:
a1,a2,,,an 为各个输入的分量
w1,w2 ,,,wn为各个输入分量对应的权重参数
b为偏置
f 为激活函数,常见的激活函数有阶跃函数,线性函数,高斯函数,tanh,sigmoid,relu等
t 为神经元的输出
4.常见的激活函数
激活函数多种多样,比如可以分为线性型、阶跃型、符号性、斜坡型等,但是本文主要介绍以下几种常见的激活函数,也是最主要的几种:

激活函数很重要的一个作用就是增加模型的非线性分割能力:
1、sigmoid 只会输出正数,以及靠近0的输出变化率最大
2、tanh和sigmoid不同的是,tanh输出可以是负数
3、Relu是输入只能大于0,如果你输入含有负数,Relu就不适合,如果你的输入是图片格式,Relu就挺常用的,因为图片的像素值作为输入时取值为[0,255]。
激活函数的作用除了前面说的增加模型的非线性分割能力外,还有以下作用:
1、提高模型鲁棒性
2、缓解梯度消失问题
3、加速模型收敛等
5.人工神经网络模型种类
本文主要介绍:
1.BP神经网络
2.RBF神经网络
3.FNN神经网络
其他的人工神经网络模型具体可见该链接:25个神经网络模型
6.人工神经网络学习方式、规则,分类
学习方法是人工神经网络研究的核心问题。
学习方式:
1、有监督:根据实际输出与期望输出的偏差取比对,按照一定的准则调整各神经元之间连接的权系数。又称导师学习,缺点是不能保证全局最优,样本空间大,收敛慢,对样本次序敏感。
2、无监督:仅通过输入调整连接权系数与阈值,学习评价标准在内部,类似聚类的操作。
规则:
1、纠错规则:利用输出的节点的外部反馈修正权重,等效与梯度下降法。
2、随机学习的规则:利用随机过程调整连接权重。
3、强化学习的规则:利用输出的正误修正权重。评判性。
4、竞争学习的规则:类似于聚类算法
分类:(按结构分)
1、前向
2、反馈
在分类与预测中,δ学习规则(误差校正学习算法)是使用最广泛的一种。误差校正学习算法根据神经网络的输出误差对神经元的连接强度进行修正,属于有指导学习。
二、感知器的介绍
1958年,计算科学家Rosenblatt提出了由两层神经元组成的神经网络。他给它起了一个名字“感知器”(Perceptron),感知器是当时首个可以学习的人工神经网络。这个时期可以看作神经网络的第一次高潮。
1.单层感知器(单层神经网络)
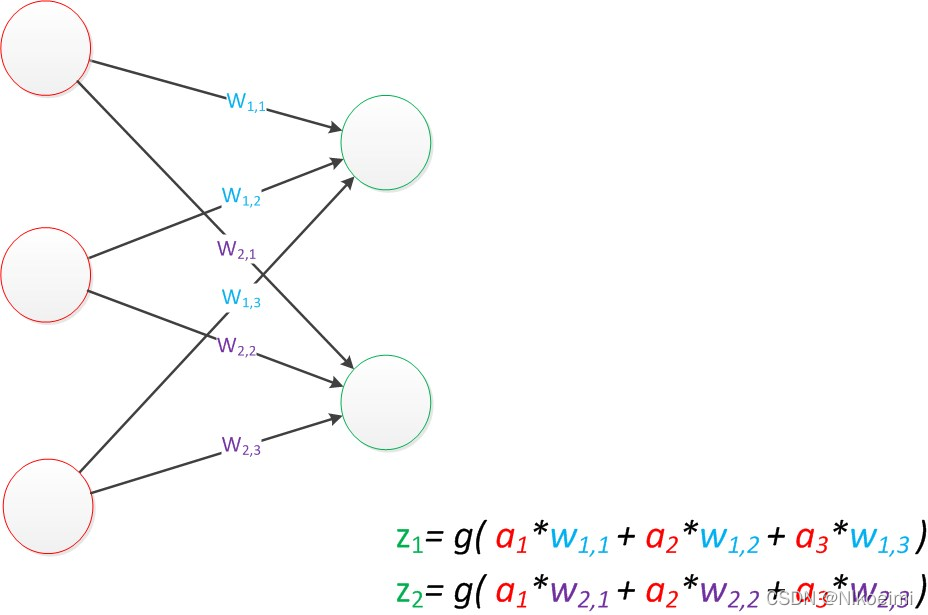
与神经元模型不同,感知器中的权值是通过训练得到的。因此,根据以前的知识我们知道,感知器类似一个逻辑回归模型,可以做线性分类任务。
2.多层感知器(两层神经网络)
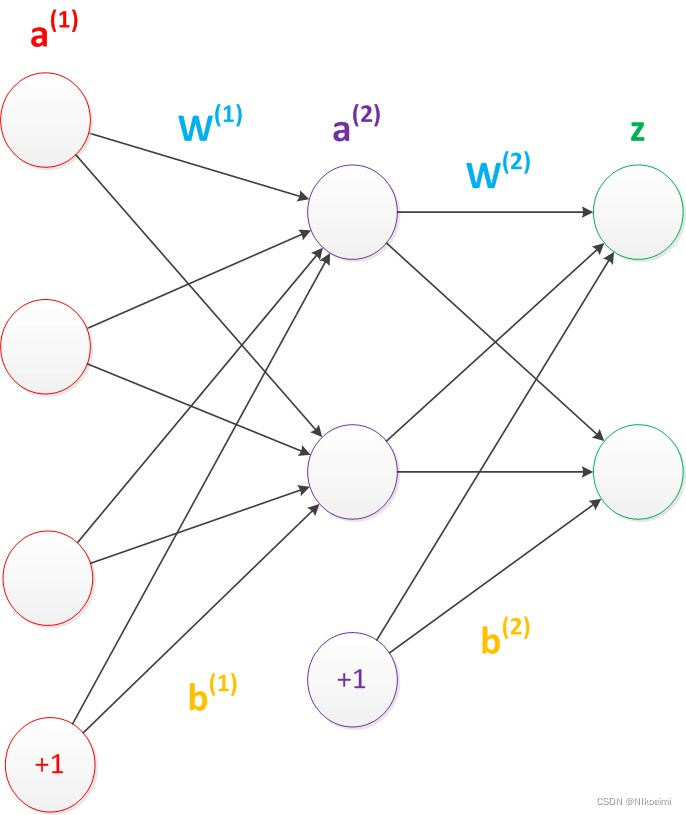
两层神经网络在多个地方的应用说明了其效用与价值。10年前困扰神经网络界的异或问题被轻松解决。神经网络在这个时候,已经可以发力于语音识别,图像识别,自动驾驶等多个领域。
三、人工神经网络算法
1.常见神经网络算法
| 算法名称 | 算法描述 |
|---|---|
| BP神经网络 | 是一种按误差逆传播算法训练的多层前馈网络,学习算法是 δ \deltaδ 学习规则,是目前应用最广泛的神经网络模型之一 |
| RBF径向神经网络 | RBF网络能够以任意精度逼近任意连续函数,从输入层到隐含层的变换是非线性的,而从隐含层到输出层的变换是线性的,特别适合于解决分类问题 |
| LM神经网络 | 是基于梯度下降法和牛顿法结合的多层前馈网络,特点:迭代次数少,收敛速度快,精确度高 |
| FNN模糊神经网络 | FNN模糊神经网络是具有模糊权系数或者输入信号是模糊量的神经网络,是模糊系统与神经网络想结合的产物,它汇聚了神经网络与模糊系统的优点,集联想、识别、自适应及模糊信息处理于一体 |
| GMDH神经网络 | GMDH网络也称为多项式网络,它是前馈神经网络中常用的一种用于预测的神经网络。它的特点是网络结构不固定,而且在训练过程中不断改变 |
| ANFIS自适应神经网络 | 神经网络镶嵌在一个全部模糊的结构之中,在不知不觉中向训练数据学习,自动产生、修正并高度概况出最佳的输入与输出变量的隶属函数以及模糊规则;另外,神经网络的各层结构与参数也都具有了明确的、易于理解的物理意义 |
2.反向传播算法(BP)
BP神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络,其算法称为BP算法,它的基本思想是梯度下降法,利用梯度搜索技术,以期使网络的实际输出值和期望输出值的误差均方差为最小。基本BP算法包括信号的前向传播和误差的反向传播两个过程。即计算误差输出时按从输入到输出的方向进行,而调整权值和阈值则从输出到输入的方向进行。正向传播时,输入信号通过隐含层作用于输出节点,经过非线性变换,产生输出信号,若实际输出与期望输出不相符,则转入误差的反向传播过程。误差反传是将输出误差通过隐含层向输入层逐层反传,并将误差分摊给各层所有单元,以从各层获得的误差信号作为调整各单元权值的依据。通过调整输入节点与隐层节点的联接强度和隐层节点与输出节点的联接强度以及阈值,使误差沿梯度方向下降,经过反复学习训练,确定与最小误差相对应的网络参数(权值和阈值),训练即告停止。此时经过训练的神经网络即能对类似样本的输入信息,自行处理输出误差最小的经过非线形转换的信息。
1.BP算法特点
反向传播算法(Back Propagation, BP),BP算法是利用输出后的误差来估计输出层的直接前导层误差,再利用这个误差估计更前一层的误差,如此一层一层的反向传播下去,就获得所有其他各层的误差估计。这样就形成了将输出层表现出的误差沿着与输入传送相反的方向逐级向网络的输入层传递的过程。以典型的三层BP网络为例,描述标准的BP算法。假设有一个有3个输入节点,4个隐层节点,1个输出节点的三层BP神经网络。
特点:
1、输入输出映射问题转化为非线性优化问题
2、由前向计算与误差反向传播组成
3、权重西修正量只与连接的两个节点相关

BP算法的学习过程由信号的正向传播与误差逆向传播两个过程组成。正向传播时,输入信号经过隐层的处理后传向输出层。若输出层节点未能得到期望的输出,则转入误差的逆向传播阶段,将输出误差按照某种子形式,通过隐层向输入层返回,并“分摊”给隐层 4 个节点与输入层 x 1、x 2 、x 3三个输入节点,从而获得各层单元的参考误差或误差信号,作为修改各个单元权值的依据。这种信号正向传播与误差逆向传播的各层权矩阵的修改过程,是周而复始的。权值不断修改的过程,也就是网络学习(或训练)的过程。此过程一直进行到网络输出误差逐渐减少到可接受的程度或达到设定的学习次数为止。
2.BP算法学习过程
算法开始后,给定学习次数上限,初始化学习次数为 0,对权值和阈值赋予小的随机数,一般在][−1,1] 之间。输入样本数据,网络正向传播,得到中间层与输出层的值。比较输出层的值与教师信号值的误差,用误差函数 E 来判断误差是否小于误差上线,如不小于误差上限,则对中间层和输出层权值和阈值进行更新,更新的算法为 δ 学习规则。更新权值和阈值后,再次将样本数据作为输入,得到中间层与输出层的值,计算误差 E 是否小于上限,学习次数是否达到指定值,如果达到,则学习结束。
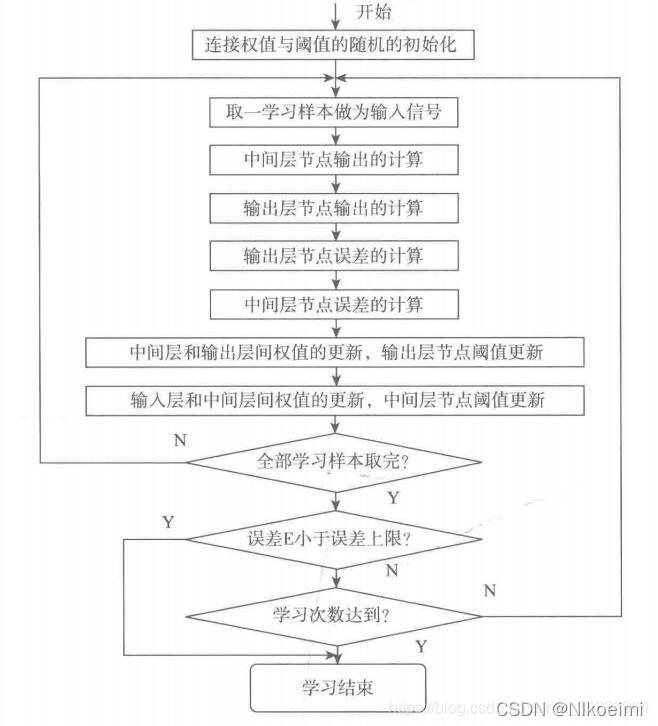
BP算法值用到均方误差函数对权值和阈值的一阶导数(梯度)信息,使得算法存在收敛速度缓慢、易陷入局部极小等缺陷。
3.BP算法实际问题
1、权重的关联性
2、对数据进行归一化和预处理。
3、样本数量的问题,网络大小的问题,越大的网络需要的样本越大,训练模式下是连接权重的5-10倍。
4、测试样本,随机划分,三分之二训练,三分之一测试。
5、训练样本必须是完备的,必须覆盖所有区域。
6、输出表示同通过编码(二进制)表示不同类别
7、适当的训练次数,防止过拟合,欠拟合。
3.径向基函数神经网络算法(RBF)
径向神经网络(RBF:Radial basis function)是一种以径向基核函数作为激活函数的前馈神经网络。RBF是20世纪80年代末提出的一种单隐层、以函数逼近为基础的前馈神经网络。随着研究日渐成熟,RBFNN以其结构简单、非线性逼近能力强以及良好的推广能力,受到各领域研究者的极大关注,被广泛应用于模式分类、函数逼近和数据挖掘等众多研究领域。
1.RBF算法特点
RBF网络一共分为三层,第一层为输入层即Input Layer,由信号源节点组成;第二层为隐藏层即图中中间的黄球,隐藏层中神经元的变换函数即径向基函数是对中心点径向对称且衰减的非负线性函数,该函数是局部响应函数。因为是局部相应函数,所以一般要根据具体问题设置相应的隐藏层神经元个数;第三层为输出层,是对输入模式做出的响应,输出层是对线性权进行调整,采用的是线性优化策略,因而学习速度较快。
2.RBF的学习方法
(1)K-均值聚类法
K-均值聚类的使用步骤:
1、得到中心和半径
2、调节权重矩阵(线性最小二乘法求权重矩阵,梯度下降法(优先使用))
(2)正交最小二乘法
3.RBF神经网络与BP神经网络进行对比
(1)RBF网络和BP网络一样可近似任何的连续非线性函数。两者的主要不同点是在非线性映射上采用了不同的作用函数。
(2) RBF网络具有惟一最佳逼近的特性,且无局部极小。
(3)求RBF网络隐节点的中心向量和标化常数是一个困难的问题。
(4)径向基函数有多种。最常用的有,高斯核函数。
(5)RBF网络用于非线性系统辨识与控制时,隐节点的中心难求。
(6) RBF网络学习速度很快。
(7)RBF网络是一种典型二层网络,BP是一种典型的三层网络。
4、RBF的MATLAB实现
演示RBF算法在计算机视觉中的应用:
SamNum = 100; % 总样本数
TestSamNum = 101; % 测试样本数
InDim = 1; % 样本输入维数
ClusterNum = 10; % 隐节点数,即聚类样本数
Overlap = 1.0; % 隐节点重叠系数
% 根据目标函数获得样本输入输出
NoiseVar = 0.1;
Noise = NoiseVar*randn(1,SamNum);
SamIn = 8*rand(1,SamNum)-4;
SamOutNoNoise = 1.1*(1-SamIn+2*SamIn.^2).*exp(-SamIn.^2/2);
SamOut = SamOutNoNoise + Noise;
TestSamIn = -4:0.08:4;
TestSamOut = 1.1*(1-TestSamIn+2*TestSamIn.^2).*exp(-TestSamIn.^2/2);
figure
hold on
grid
plot(SamIn,SamOut,'k+')
plot(TestSamIn,TestSamOut,'k--')
xlabel('Input x');
ylabel('Output y');
Centers = SamIn(:,1:ClusterNum);
NumberInClusters = zeros(ClusterNum,1); % 各类中的样本数,初始化为零
IndexInClusters = zeros(ClusterNum,SamNum); % 各类所含样本的索引号
while 1,
NumberInClusters = zeros(ClusterNum,1); % 各类中的样本数,初始化为零
IndexInClusters = zeros(ClusterNum,SamNum); % 各类所含样本的索引号
% 按最小距离原则对所有样本进行分类
for i = 1:SamNum
AllDistance = dist(Centers',SamIn(:,i));
[MinDist,Pos] = min(AllDistance);
NumberInClusters(Pos) = NumberInClusters(Pos) + 1;
IndexInClusters(Pos,NumberInClusters(Pos)) = i;
end
% 保存旧的聚类中心
OldCenters = Centers;
for i = 1:ClusterNum
Index = IndexInClusters(i,1:NumberInClusters(i));
Centers(:,i) = mean(SamIn(:,Index)')';
end
% 判断新旧聚类中心是否一致,是则结束聚类
EqualNum = sum(sum(Centers==OldCenters));
if EqualNum == InDim*ClusterNum,
break,
end
end
% 计算各隐节点的扩展常数(宽度)
AllDistances = dist(Centers',Centers); % 计算隐节点数据中心间的距离(矩阵)
Maximum = max(max(AllDistances)); % 找出其中最大的一个距离
for i = 1:ClusterNum % 将对角线上的0 替换为较大的值
AllDistances(i,i) = Maximum+1;
end
Spreads = Overlap*min(AllDistances)'; % 以隐节点间的最小距离作为扩展常数
% 计算各隐节点的输出权值
Distance = dist(Centers',SamIn); % 计算各样本输入离各数据中心的距离
SpreadsMat = repmat(Spreads,1,SamNum);
HiddenUnitOut = radbas(Distance./SpreadsMat); % 计算隐节点输出阵
HiddenUnitOutEx = [HiddenUnitOut' ones(SamNum,1)]'; % 考虑偏移
W2Ex = SamOut*pinv(HiddenUnitOutEx); % 求广义输出权值
W2 = W2Ex(:,1:ClusterNum); % 输出权值
B2 = W2Ex(:,ClusterNum+1); % 偏移
% 测试
TestDistance = dist(Centers',TestSamIn);
TestSpreadsMat = repmat(Spreads,1,TestSamNum);
TestHiddenUnitOut = radbas(TestDistance./TestSpreadsMat);
TestNNOut = W2*TestHiddenUnitOut+B2;
plot(TestSamIn,TestNNOut,'k-')
W2
B2
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
4.模糊神经网络算法(FNN)
模糊神经网络(Fuzzy Neural Network, FNN),神经网络与模糊系统的结合,在处理大规模的模糊应用问题方面将表现出优良效果。模糊神经网络本质是将模糊输入信号和模糊权值输入常规的神经网络。其结构上像神经网络,功能上是模糊系统。学习算法是模糊神经网络优化权系数的关键。
1.FNN算法特点
模糊神经网络虽然也是局部逼近网络,但是它是按照模糊系统模型建立的,网络中的各个结点及所有参数均有明显的物理意义,因此这些参数的初值可以根据系统或定性的知识来加以确定,然后利用上述的学习算法可以很快收敛到要求的输入输出关系,这是模糊神经网络比前面单纯的神经网络的优点所在。同时由于它具有神经网络的结构,因而参数的学习和调整比较容易,这是它比单纯的模糊逻辑系统的优点所在。
2.FNN算法结构
模糊神经网络将模糊系统和神经网络相结合,充分考虑了二者的互补性,集逻辑推理、语言计算、非线性动力学于一体,具有学习、联想、识别、自适应和模糊信息处理能力等功能。
本质: 就是将常规的神经网络输入模糊输入信号和模糊权值。
输入层: 模糊系统的输入信号
输出层: 模糊系统的输出信号
隐藏层: 隶属函数和模糊规则
利用神经网络的学习方法,根据输入输出的学习样本自动设计和调整模糊系统的设计参数,实现模糊系统的自学习和自适应功能。结构上像神经网络,功能上是模糊系统,这是目前研究和应用最多的一类模糊神经网络
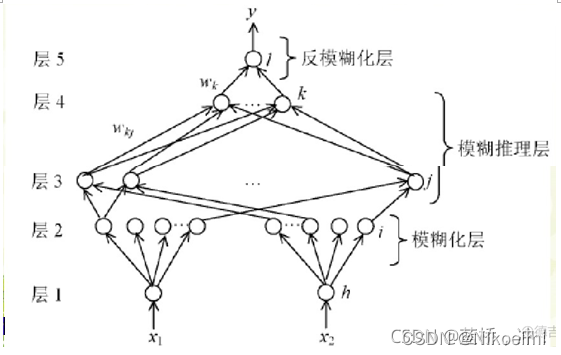
第1层:输入层,为精确值。节点个数为输入变量的个数。
第2层:输入变量的隶属函数层,实现输入变量的模糊化,x1有m个集合,x2有n个集合。
第3层:也称“与”层,该层节点个数为模糊规则数。该层每个节点只与第二层中m个节点中的一个和n个节点中的一个相连,共有m×n个节点,也就是有m×n条规则。
第4层:也称“或”层,节点数为输出变量模糊度划分的个数q。
该层与第三层的连接为全互连,连接权值为wkj ,其中
k=1.2…m×n
j=1.2…q
(权值代表了每条规则的置信度,训练中可调。)
第5层:清晰化层,节点数为输出变量的个数。该层与第四层的连接为全互连,该层将第四层各个节点的输出转换为输出变量的精确值。
第2层的隶属函数参数和3、4层间及4、5层间的连接权是可以调整的
学习算法是模糊神经网络优化权系数的关键。模糊神经网络的学习算法,大多来自神经网络,如BP算法、RBF算法等。
四、matlab实现神经网络
1.不使用神经网络工具箱实现BP
numberOfSample = 20; %输入样本数量
%取测试样本数量等于输入(训练集)样本数量,因为输入样本(训练集)容量较少,否则一般必须用新鲜数据进行测试
numberOfTestSample = 20;
numberOfForcastSample = 2;
numberOfHiddenNeure = 8;
inputDimension = 3;
outputDimension = 2;
%准备好训练集
%人数(单位:万人)
numberOfPeople=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63];
%机动车数(单位:万辆)
numberOfAutomobile=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6 2.7 2.85 2.95 3.1];
%公路面积(单位:万平方公里)
roadArea=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 0.56 0.59 0.59 0.67 0.69 0.79];
%公路客运量(单位:万人)
passengerVolume = [5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 22598 25107 33442 36836 40548 42927 43462];
%公路货运量(单位:万吨)
freightVolume = [1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 13320 16762 18673 20724 20803 21804];
%由系统时钟种子产生随机数
rand('state', sum(100*clock));
%输入数据矩阵
input = [numberOfPeople; numberOfAutomobile; roadArea];
%目标(输出)数据矩阵
output = [passengerVolume; freightVolume];
%对训练集中的输入数据矩阵和目标数据矩阵进行归一化处理
[sampleInput, minp, maxp, tmp, mint, maxt] = premnmx(input, output);
%噪声强度
noiseIntensity = 0.01;
%利用正态分布产生噪声
noise = noiseIntensity * randn(outputDimension, numberOfSample);
%给样本输出矩阵tmp添加噪声,防止网络过度拟合
sampleOutput = tmp + noise;
%取测试样本输入(输出)与输入样本相同,因为输入样本(训练集)容量较少,否则一般必须用新鲜数据进行测试
testSampleInput = sampleInput;
testSampleOutput = sampleOutput;
%最大训练次数
maxEpochs = 50000;
%网络的学习速率
learningRate = 0.035;
%训练网络所要达到的目标误差
error0 = 0.65*10^(-3);
%初始化输入层与隐含层之间的权值
W1 = 0.5 * rand(numberOfHiddenNeure, inputDimension) - 0.1;
%初始化输入层与隐含层之间的阈值
B1 = 0.5 * rand(numberOfHiddenNeure, 1) - 0.1;
%初始化输出层与隐含层之间的权值
W2 = 0.5 * rand(outputDimension, numberOfHiddenNeure) - 0.1;
%初始化输出层与隐含层之间的阈值
B2 = 0.5 * rand(outputDimension, 1) - 0.1;
%保存能量函数(误差平方和)的历史记录
errorHistory = [];
for i = 1:maxEpochs
%隐含层输出
hiddenOutput = logsig(W1 * sampleInput + repmat(B1, 1, numberOfSample));
%输出层输出
networkOutput = W2 * hiddenOutput + repmat(B2, 1, numberOfSample);
%实际输出与网络输出之差
error = sampleOutput - networkOutput;
%计算能量函数(误差平方和)
E = sumsqr(error);
errorHistory = [errorHistory E];
if E < error0
break;
end
%以下依据能量函数的负梯度下降原理对权值和阈值进行调整
delta2 = error;
delta1 = W2' * delta2.*hiddenOutput.*(1 - hiddenOutput);
dW2 = delta2 * hiddenOutput';
dB2 = delta2 * ones(numberOfSample, 1);
dW1 = delta1 * sampleInput';
dB1 = delta1 * ones(numberOfSample, 1);
W2 = W2 + learningRate * dW2;
B2 = B2 + learningRate * dB2;
W1 = W1 + learningRate * dW1;
B1 = B1 + learningRate * dB1;
end
%下面对已经训练好的网络进行(仿真)测试
%对测试样本进行处理
testHiddenOutput = logsig(W1 * testSampleInput + repmat(B1, 1, numberOfTestSample));
testNetworkOutput = W2 * testHiddenOutput + repmat(B2, 1, numberOfTestSample);
%还原网络输出层的结果(反归一化)
a = postmnmx(testNetworkOutput, mint, maxt);
%绘制测试样本神经网络输出和实际样本输出的对比图(figure(1))--------------------------------------
t = 1990:2009;
%测试样本网络输出客运量
a1 = a(1,:);
%测试样本网络输出货运量
a2 = a(2,:);
figure(1);
subplot(2, 1, 1); plot(t, a1, 'ro', t, passengerVolume, 'b+');
legend('网络输出客运量', '实际客运量');
xlabel('年份'); ylabel('客运量/万人');
title('神经网络客运量学习与测试对比图');
grid on;
subplot(2, 1, 2); plot(t, a2, 'ro', t, freightVolume, 'b+');
legend('网络输出货运量', '实际货运量');
xlabel('年份'); ylabel('货运量/万吨');
title('神经网络货运量学习与测试对比图');
grid on;
%使用训练好的神经网络对新输入数据进行预测
%新输入数据(2010年和2011年的相关数据)
newInput = [73.39 75.55; 3.9635 4.0975; 0.9880 1.0268];
%利用原始输入数据(训练集的输入数据)的归一化参数对新输入数据进行归一化
newInput = tramnmx(newInput, minp, maxp);
newHiddenOutput = logsig(W1 * newInput + repmat(B1, 1, numberOfForcastSample));
newOutput = W2 * newHiddenOutput + repmat(B2, 1, numberOfForcastSample);
newOutput = postmnmx(newOutput, mint, maxt);
disp('预测2010和2011年的公路客运量分别为(单位:万人):');
newOutput(1,:)
disp('预测2010和2011年的公路货运量分别为(单位:万吨):');
newOutput(2,:)
%在figure(1)的基础上绘制2010和2011年的预测情况-------------------------------------------------
figure(2);
t1 = 1990:2011;
subplot(2, 1, 1); plot(t1, [a1 newOutput(1,:)], 'ro', t, passengerVolume, 'b+');
legend('网络输出客运量', '实际客运量');
xlabel('年份'); ylabel('客运量/万人');
title('神经网络客运量学习与测试对比图(添加了预测数据)');
grid on;
subplot(2, 1, 2); plot(t1, [a2 newOutput(2,:)], 'ro', t, freightVolume, 'b+');
legend('网络输出货运量', '实际货运量');
xlabel('年份'); ylabel('货运量/万吨');
title('神经网络货运量学习与测试对比图(添加了预测数据)');
grid on;
%观察能量函数(误差平方和)在训练神经网络过程中的变化情况------------------------------------------
figure(3);
n = length(errorHistory);
t3 = 1:n;
plot(t3, errorHistory, 'r-');
%为了更加清楚地观察出能量函数值的变化情况,这里我只绘制前100次的训练情况
xlim([1 100]);
xlabel('训练过程');
ylabel('能量函数值');
title('能量函数(误差平方和)在训练神经网络过程中的变化图');
grid on;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
效果如下:
预测2010和2011年的公路客运量分别为(单位:万人):
ans =
1.0e+04 *4.6188 4.6601
预测2010和2011年的公路货运量分别为(单位:万吨):
ans =
1.0e+04 *2.1521 2.1519
2.使用神经网络工具箱实现BP
%准备好训练集
%人数(单位:万人)
numberOfPeople=[20.55 22.44 25.37 27.13 29.45 30.10 30.96 34.06 36.42 38.09 39.13 39.99 41.93 44.59 47.30 52.89 55.73 56.76 59.17 60.63];
%机动车数(单位:万辆)
numberOfAutomobile=[0.6 0.75 0.85 0.9 1.05 1.35 1.45 1.6 1.7 1.85 2.15 2.2 2.25 2.35 2.5 2.6 2.7 2.85 2.95 3.1];
%公路面积(单位:万平方公里)
roadArea=[0.09 0.11 0.11 0.14 0.20 0.23 0.23 0.32 0.32 0.34 0.36 0.36 0.38 0.49 0.56 0.59 0.59 0.67 0.69 0.79];
%公路客运量(单位:万人)
passengerVolume = [5126 6217 7730 9145 10460 11387 12353 15750 18304 19836 21024 19490 20433 22598 25107 33442 36836 40548 42927 43462];
%公路货运量(单位:万吨)
freightVolume = [1237 1379 1385 1399 1663 1714 1834 4322 8132 8936 11099 11203 10524 11115 13320 16762 18673 20724 20803 21804];
%输入数据矩阵
p = [numberOfPeople; numberOfAutomobile; roadArea];
%目标(输出)数据矩阵
t = [passengerVolume; freightVolume];
%对训练集中的输入数据矩阵和目标数据矩阵进行归一化处理
[pn, inputStr] = mapminmax(p);
[tn, outputStr] = mapminmax(t);
%建立BP神经网络
net = newff(pn, tn, [3 7 2], {'purelin', 'logsig', 'purelin'});
%每10轮回显示一次结果
net.trainParam.show = 10;
%最大训练次数
net.trainParam.epochs = 5000;
%网络的学习速率
net.trainParam.lr = 0.05;
%训练网络所要达到的目标误差
net.trainParam.goal = 0.65 * 10^(-3);
%网络误差如果连续6次迭代都没变化,则matlab会默认终止训练。为了让程序继续运行,用以下命令取消这条设置
net.divideFcn = '';
%开始训练网络
net = train(net, pn, tn);
%使用训练好的网络,基于训练集的数据对BP网络进行仿真得到网络输出结果
%(因为输入样本(训练集)容量较少,否则一般必须用新鲜数据进行仿真测试)
answer = sim(net, pn);
%反归一化
answer1 = mapminmax('reverse', answer, outputStr);
%绘制测试样本神经网络输出和实际样本输出的对比图(figure(1))-------------------------------------------
t = 1990:2009;
%测试样本网络输出客运量
a1 = answer1(1,:);
%测试样本网络输出货运量
a2 = answer1(2,:);
figure(1);
subplot(2, 1, 1); plot(t, a1, 'ro', t, passengerVolume, 'b+');
legend('网络输出客运量', '实际客运量');
xlabel('年份'); ylabel('客运量/万人');
title('神经网络客运量学习与测试对比图');
grid on;
subplot(2, 1, 2); plot(t, a2, 'ro', t, freightVolume, 'b+');
legend('网络输出货运量', '实际货运量');
xlabel('年份'); ylabel('货运量/万吨');
title('神经网络货运量学习与测试对比图');
grid on;
%使用训练好的神经网络对新输入数据进行预测
%新输入数据(2010年和2011年的相关数据)
newInput = [73.39 75.55; 3.9635 4.0975; 0.9880 1.0268];
%利用原始输入数据(训练集的输入数据)的归一化参数对新输入数据进行归一化
newInput = mapminmax('apply', newInput, inputStr);
%进行仿真
newOutput = sim(net, newInput);
%反归一化
newOutput = mapminmax('reverse',newOutput, outputStr);
disp('预测2010和2011年的公路客运量分别为(单位:万人):');
newOutput(1,:)
disp('预测2010和2011年的公路货运量分别为(单位:万吨):');
newOutput(2,:)
%在figure(1)的基础上绘制2010和2011年的预测情况-------------------------------------------------------
figure(2);
t1 = 1990:2011;
subplot(2, 1, 1); plot(t1, [a1 newOutput(1,:)], 'ro', t, passengerVolume, 'b+');
legend('网络输出客运量', '实际客运量');
xlabel('年份'); ylabel('客运量/万人');
title('神经网络客运量学习与测试对比图(添加了预测数据)');
grid on;
subplot(2, 1, 2); plot(t1, [a2 newOutput(2,:)], 'ro', t, freightVolume, 'b+');
legend('网络输出货运量', '实际货运量');
xlabel('年份'); ylabel('货运量/万吨');
title('神经网络货运量学习与测试对比图(添加了预测数据)');
grid on;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
运行结果如下:
预测2010和2011年的公路客运量分别为(单位:万人):
ans =
1.0e+04 *4.4384 4.4656
预测2010和2011年的公路货运量分别为(单位:万吨):
ans =
1.0e+04 *2.1042 2.1139
五、python实现神经网络
示例1
神经网络算法预测销量高低:
import pandas as pd
from keras.models import Sequential
from keras.layers.core import Dense, Activation
def cm_plot(y, yp):
from sklearn.metrics import confusion_matrix # 导入混淆矩阵函数
cm = confusion_matrix(y, yp) # 混淆矩阵
import matplotlib.pyplot as plt # 导入作图库
plt.matshow(cm, cmap=plt.cm.Greens) # 画混淆矩阵图,配色风格使用cm.Greens,更多风格请参考官网。
plt.colorbar() # 颜色标签
for x in range(len(cm)): # 数据标签
for y in range(len(cm)):
plt.annotate(cm[x, y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True label') # 坐标轴标签
plt.xlabel('Predicted label') # 坐标轴标签
return plt
# 参数初始化
inputfile = '../Data/sales_data.xls'
data = pd.read_excel(inputfile, index_col=u'序号') # 导入数据
# 数据是类别标签,要将它转换为数据
# 用1来表示“好” “是” “高” 这 3 个属性,用 0 来表示 “坏” “否” “低”
data[data == u'好'] = 1
data[data == u'是'] = 1
data[data == u'高'] = 1
data[data != 1] = 0
x = data.iloc[:, :3].values.astype(int)
y = data.iloc[:, 3].values.astype(int)
model = Sequential() # 建立模型
model.add(Dense(input_dim=3, units=10, activation='relu')) # 用relu函数作为激活函数,能够大幅度提供准确度
model.add(Dense(input_dim=10, units=1, activation='sigmoid')) # 由于是 0-1 输出,用 sigmoid 函数作为激活函数
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy']) # 求解方法我们指定用 adam,还有sgd、rmsprop等可选
model.fit(x, y, epochs=1000, batch_size=10) # 训练模型,学习1000次,每次以10个样本为一个batch进行迭代
yp = model.predict_classes(x).reshape(len(y)) # 分类预测
cm_plot(y, yp).show() # 显示混淆矩阵可视化结果
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
效果如下:
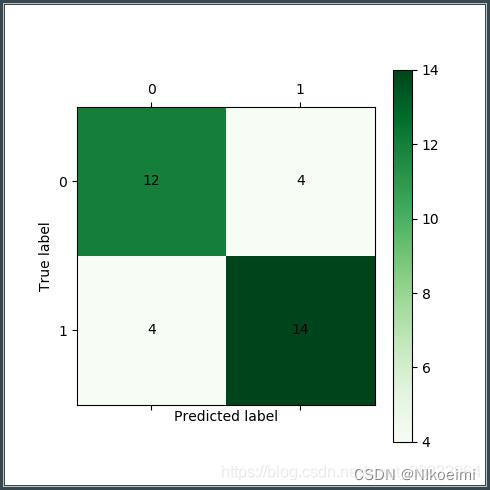
示例2
推测出每个人的性别:
import numpy as np
def sigmoid(x):
# our activation function: f(x) = 1 / (1 * e^(-x))
return 1 / (1 + np.exp(-x))
class Neuron():
def __init__(self, weights, bias):
self.weights = weights
self.bias = bias
def feedforward(self, inputs):
# weight inputs, add bias, then use the activation function
total = np.dot(self.weights, inputs) + self.bias
return sigmoid(total)
weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4
n = Neuron(weights, bias)
# inputs
x = np.array([2, 3]) # x1 = 2, x2 = 3
print(n.feedforward(x)) # 0.9990889488055994
class OurNeuralNetworks():
"""
A neural network with:
- 2 inputs
- a hidden layer with 2 neurons (h1, h2)
- an output layer with 1 neuron (o1)
Each neural has the same weights and bias:
- w = [0, 1]
- b = 0
"""
def __init__(self):
weights = np.array([0, 1])
bias = 0
# The Neuron class here is from the previous section
self.h1 = Neuron(weights, bias)
self.h2 = Neuron(weights, bias)
self.o1 = Neuron(weights, bias)
def feedforward(self, x):
out_h1 = self.h1.feedforward(x)
out_h2 = self.h2.feedforward(x)
# The inputs for o1 are the outputs from h1 and h2
out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))
return out_o1
network = OurNeuralNetworks()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421
def mse_loss(y_true, y_pred):
# y_true and y_pred are numpy arrays of the same length
return ((y_true - y_pred) ** 2).mean()
y_true = np.array([1, 0, 0, 1])
y_pred = np.array([0, 0, 0, 0])
print(mse_loss(y_true, y_pred)) # 0.5
def sigmoid(x):
# Sigmoid activation function: f(x) = 1 / (1 + e^(-x))
return 1 / (1 + np.exp(-x))
def deriv_sigmoid(x):
# Derivative of sigmoid: f'(x) = f(x) * (1 - f(x))
fx = sigmoid(x)
return fx * (1 - fx)
def mse_loss(y_true, y_pred):
# y_true and y_pred are numpy arrays of the same length
return ((y_true - y_pred) ** 2).mean()
class OurNeuralNetwork():
"""
A neural network with:
- 2 inputs
- a hidden layer with 2 neurons (h1, h2)
- an output layer with 1 neuron (o1)
*** DISCLAIMER ***
The code below is intend to be simple and educational, NOT optimal.
Real neural net code looks nothing like this. Do NOT use this code.
Instead, read/run it to understand how this specific network works.
"""
def __init__(self):
# weights
self.w1 = np.random.normal()
self.w2 = np.random.normal()
self.w3 = np.random.normal()
self.w4 = np.random.normal()
self.w5 = np.random.normal()
self.w6 = np.random.normal()
# biases
self.b1 = np.random.normal()
self.b2 = np.random.normal()
self.b3 = np.random.normal()
def feedforward(self, x):
# x is a numpy array with 2 elements, for example [input1, input2]
h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
return o1
def train(self, data, all_y_trues):
"""
- data is a (n x 2) numpy array, n = # samples in the dataset.
- all_y_trues is a numpy array with n elements.
Elements in all_y_trues correspond to those in data.
"""
learn_rate = 0.1
epochs = 1000 # number of times to loop through the entire dataset
for epoch in range(epochs):
for x, y_true in zip(data, all_y_trues):
# - - - Do a feedforward (we'll need these values later)
sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
h1 = sigmoid(sum_h1)
sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
h2 = sigmoid(sum_h2)
sum_o1 = self.w5 * x[0] + self.w6 * x[1] + self.b3
o1 = sigmoid(sum_o1)
y_pred = o1
# - - - Calculate partial derivatives.
# - - - Naming: d_L_d_w1 represents "partial L / partial w1"
d_L_d_ypred = -2 * (y_true - y_pred)
# Neuron o1
d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
d_ypred_d_b3 = deriv_sigmoid(sum_o1)
d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)
# Neuron h1
d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
d_h1_d_b1 = deriv_sigmoid(sum_h1)
# Neuron h2
d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
d_h2_d_w4 = x[0] * deriv_sigmoid(sum_h2)
d_h2_d_b2 = deriv_sigmoid(sum_h2)
# - - - update weights and biases
# Neuron o1
self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3
# Neuron h1
self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1
# Neuron h2
self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2
# - - - Calculate total loss at the end of each epoch
if epoch % 10 == 0:
y_preds = np.apply_along_axis(self.feedforward, 1, data)
loss = mse_loss(all_y_trues, y_preds)
print("Epoch %d loss: %.3f", (epoch, loss))
# Define dataset
data = np.array([
[-2, -1], # Alice
[25, 6], # Bob
[17, 4], # Charlie
[-15, -6] # diana
])
all_y_trues = np.array([
1, # Alice
0, # Bob
0, # Charlie
1 # diana
])
# Train our neural network!
network = OurNeuralNetwork()
network.train(data, all_y_trues)
# Make some predictions
emily = np.array([-7, -3]) # 128 pounds, 63 inches
frank = np.array([20, 2]) # 155 pounds, 68 inches
print("Emily: %.3f" % network.feedforward(emily)) # 0.951 - F
print("Frank: %.3f" % network.feedforward(frank)) # 0.039 - M
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198


