C语言数据结构复杂度_大o表示法给出下列程序的时间复杂度为 。void bubblesort(t arr[], int n

前言

从这篇博客开始为数据结构与算法的相关内容，数据结构比较难，博主建议大家每学完一章便去力扣刷题，前期可以多看几遍答案在去敲，学好数据结构需要大量的代码作为支撑，光有概念是不行的。若想要看数据结构与算法的相关书籍，博主强推《大话数据结构》，个人认为此书对新手很友好。另外在数据结构的学习过程中，也可以借助画图来理解。
PS：本篇博客中的size_t代表unsigned int。

什么是数据结构

数据结构(Data Structure)是计算机存储、组织数据的方式，指相互之间存在一种或多种特定关系的
数据元素的集合。（基础概念，了解就行）

什么是算法

算法(Algorithm):就是定义良好的计算过程，他取一个或一组的值为输入，并产生出一个或一组值作为
输出。简单来说算法就是一系列的计算步骤，用来将输入数据转化成输出结果。

算法效率

一个算法的好坏改如何评价？对其好坏的理解又是什么？

算法的复杂度

算法在编写成可执行程序后，运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏，一般
是从时间和空间两个维度来衡量的，即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢，而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算
机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计
算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
而在当今的校招或是企业面试中都少不了对复杂度的考察

上图为腾讯c++后台开发一面的问题。

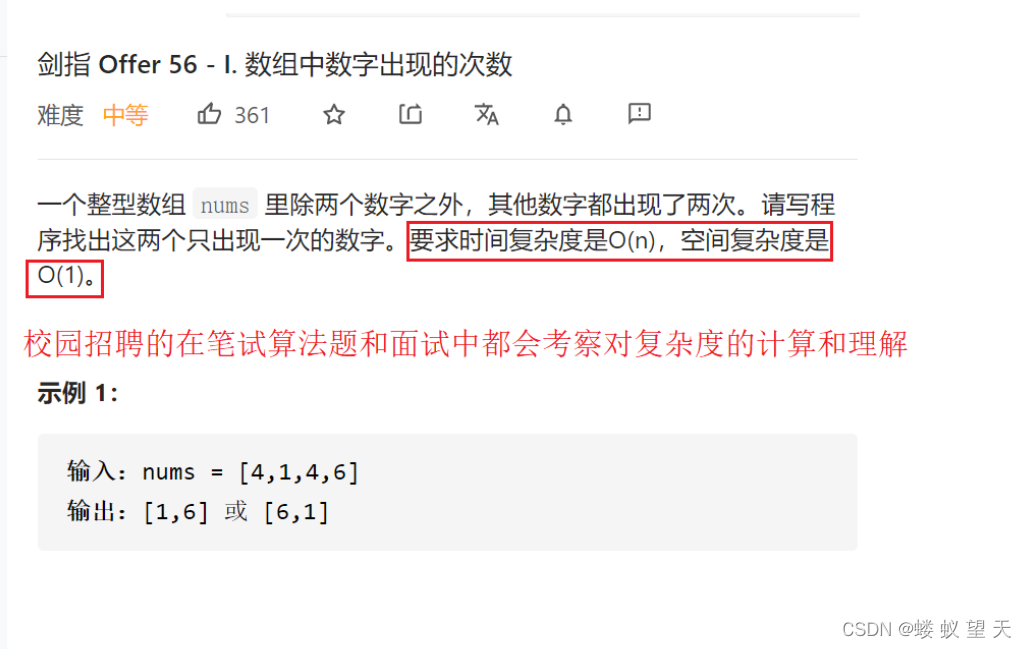
时间复杂度

时间复杂度的概念

时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数，（数学上那种函数），它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？是可以都上机测试，但是这很麻烦，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。
即：找到某条基本语句与问题规模N之间的数学表达式，就是算出了该算法的时间复杂度。

// 请计算一下Func1中++count语句总共执行了多少次？
void Func1(int N)
{
	int count = 0;
	for (int i = 0; i < N; ++i)
	{
		for (int j = 0; j < N; ++j)
		{
			++count;
		}
	}
	for (int k = 0; k < 2 * N; ++k)
	{
		++count;
	}
	int M = 10;
	while (M--)
	{
		++count;
	}
	printf("%d\n", count);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

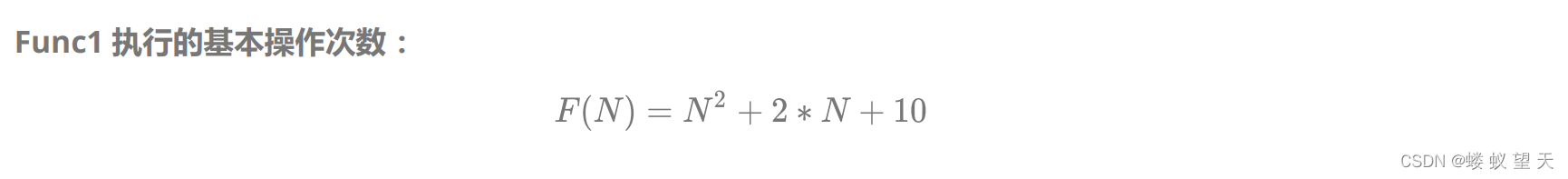
但在实际计算时间复杂度时，我们并不需要这样精准的计算，我们只要知道大概的执行次数就好，所以我们引入了一种方法叫大O的渐进表示法。

大O的渐进表示法

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。
推导大O阶方法：
1、用常数1取代运行时间中的所有加法常数（不包含系数）。
2、在修改后的运行次数函数中，只保留最高阶项（如原先时间复杂度为n²+2n，那么运用大O渐进表示法后，其时间复杂度为n²，还有就是常数也要去掉）。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。
（如时间复杂度为2n²+2n，运用大O渐进表示法后，其时间复杂度为n²）。

我们就以Func1的时间复杂度为例，若使N变得无限大，n²+2n+10与n²差别并不大，所以在以后描述时间复杂度时都用大O渐进表示法去描述。

另外有些算法的时间复杂度存在最好、平均和最坏情况：
最坏情况：任意输入规模的最大运行次数(上界)
平均情况：任意输入规模的期望运行次数
最好情况：任意输入规模的最小运行次数(下界)
例如：在一个长度为N数组中搜索一个数据x
最好情况：1次找到
最坏情况：N次找到
平均情况：N/2次找到
在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)。

常见时间复杂度计算举例

例1：

void Func2(int N)
{
	int count = 0;
	for (int k = 0; k < 2 * N; ++k)
	{
		++count;
	}
	int M = 10;
	while (M--)
	{
		++count;
	}
	printf("%d\n", count);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

求出其函数式为2n+10，根据大O法第一条用1代替所有加法常数，将10变成1为2n+1，根据第二条保留最高阶变成2n，第三条最高阶系数补位1，去除最高阶系数，所以其时间复杂度最终表示为O(n)。常规时间复杂度就如此分析。
例2：

void Func3(int N, int M)
{
	int count = 0;
	for (int k = 0; k < M; ++k)
	{
		++count;
	}
	for (int k = 0; k < N; ++k)
	{
		++count;
	}
	printf("%d\n", count);
}
1
2
3
4
5
6
7
8
9
10
11
12
13

这道题的时间复杂度表示为O(M+N),因为M不是已知常量，其与N一样是未知量且阶数与N相同所以根据大O表示方法为O(M+N)。
例3：

void Func4(int N)
{
	int count = 0;
	for (int k = 0; k < 100; ++k)
	{
		++count;
	}
	printf("%d\n", count);
}
1
2
3
4
5
6
7
8
9

首先这里没有变量，执行次数为100次，根据大O表示法，把所有加数常数变为1，所以其时间复杂度为O(1)。
例4：

const char* strchr(const char* str, int character);
1

这个函数的作用是在字符串str中寻找字符character。
例如有一个字符个数为n的字符串，那么假设这个字符串中有character这个字符，那么可知，找到这个字符最少的执行次数为1，所以最好的时间复杂度为O(1),而最坏的时间复杂度为O(n)，平均时间复杂度为O（n/2），而在我们计算时间复杂度时一般只看最坏情况下的，所以这个程序的时间复杂度为O（n）。
例5：

void BubbleSort(int* a, int n)
{
	assert(a);//断言
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

例5是一个冒泡排序，其基本操作执行最好N次，最坏执行了(N*(N+1)/2次（等差数列），通过推导大O阶方法+时间复杂度一般看最坏，时间复杂度为 O(N^2)。
例6：

int BinarySearch(int* a, int n, int x)
{
	assert(a);
	int begin = 0;
	int end = n - 1;
	// [begin, end]：begin和end是左闭右闭区间，因此有=号
	while (begin <= end)
	{
		int mid = begin + ((end - begin) >> 1);
		if (a[mid] < x)
			begin = mid + 1;
		else if (a[mid] > x)
			end = mid - 1;
		else
			return mid;
	}
	return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

如上图是一个二分查找，进行二分查找的前提是需要对查找的对象进行排序。如一个排序好的数组，要找一个数，对其进行二分查找，那么就从中间开始，若这个数大于中间值，那么从右半部分的中间值开始查找，若数小于中间值，则从其左半部分的中间值开始查找，以此类推。

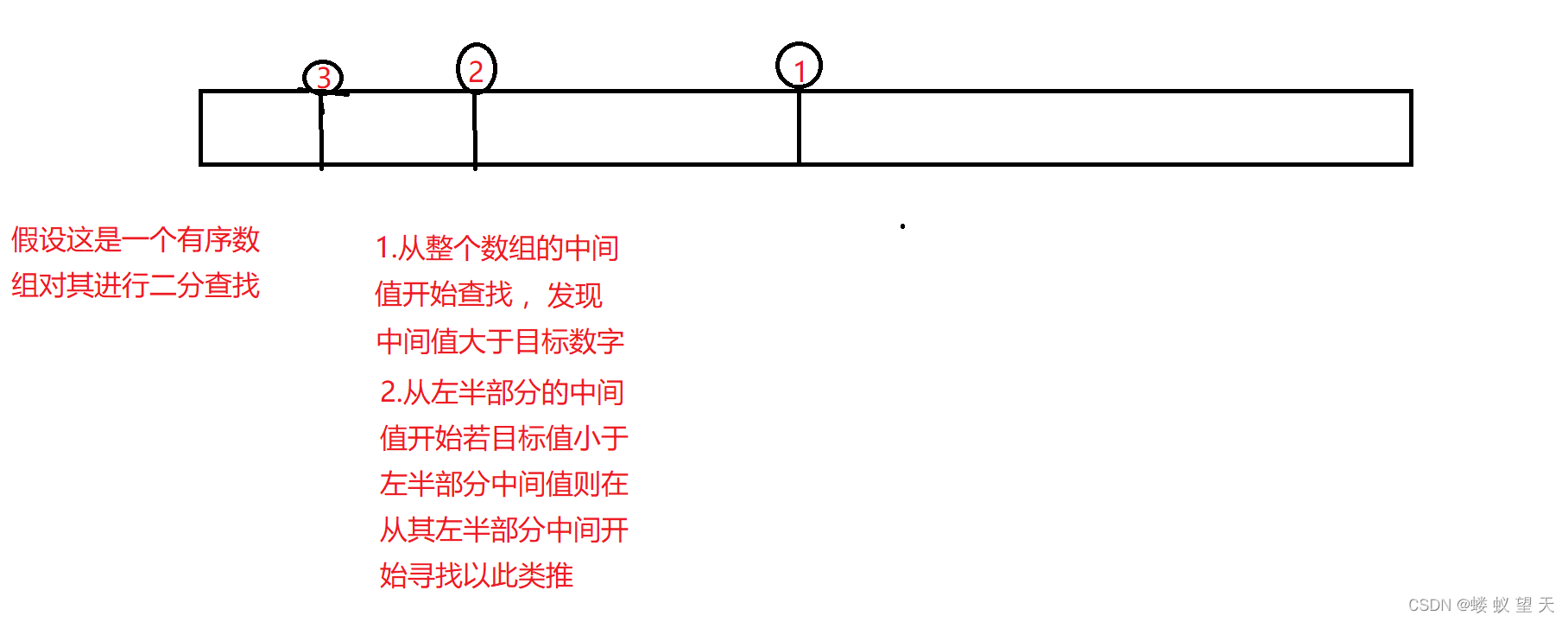
所以其时间复杂度为 O(logN)，这里再次提醒一下，时间复杂度是一个程序运行的次数，不是程序运行的时间，因为机器的执行速度不同一个相同的程序，在神威太湖之光上可能0ms就执行完毕，而在我们的电脑山可能要100ms。
正在说一点在时间复杂度计算中log一般是时间复杂度最好的代表，若你编写的算法时间复杂度出现了log，那么你的算法是很nice的，还有就是在时间复杂度计算中若log的底数为2，那么我们一般省略不写，若是其他底数，一般都要写上。
例7：

long long Fac(size_t N)
{
	if (0 == N)
		return 1;
	return Fac(N - 1) * N;
}
1
2
3
4
5
6

通过计算分析发现基本操作递归了N次，时间复杂度为O(N)。

空间复杂度

空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。
空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。
注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因
此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
空间复杂度大O渐进表示法的规则与时间复杂度的大O渐进表示法规则一致。
例1：

void BubbleSort(int* a, int n)
{
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

如上代码，end是一个变量exchange是一个变量（重复创建相同变量算一个），i是一个变量，所以变量总数为3
（不算函数的形参），经过大O法，此程序的空间复杂度为O（1）。
例2:

long long* Fibonacci(size_t n)
{
	if (n == 0)
		return NULL;
	long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n; ++i)
	{
		fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
	}
	return fibArray;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

此程序中long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));创建了n+1个变量空间，所以其空间复杂度为O（n）。
例3：

long long Fac(size_t N)
{
	if (N == 0)
		return 1;
	return Fac(N - 1) * N;
}
1
2
3
4
5
6

递归调用了N次，开辟了N个栈帧（函数所用的空间），每个栈帧使用了常数个空间。空间复杂度为O(N)。
空间复杂度我们稍作了解就好，因为现在科技足够发达，我们不用为空间不足而操心，在面试和校招时大部分考的也是时间复杂度。

常见复杂度对比

这里大家了解一下常见的复杂度有哪些种类就好：

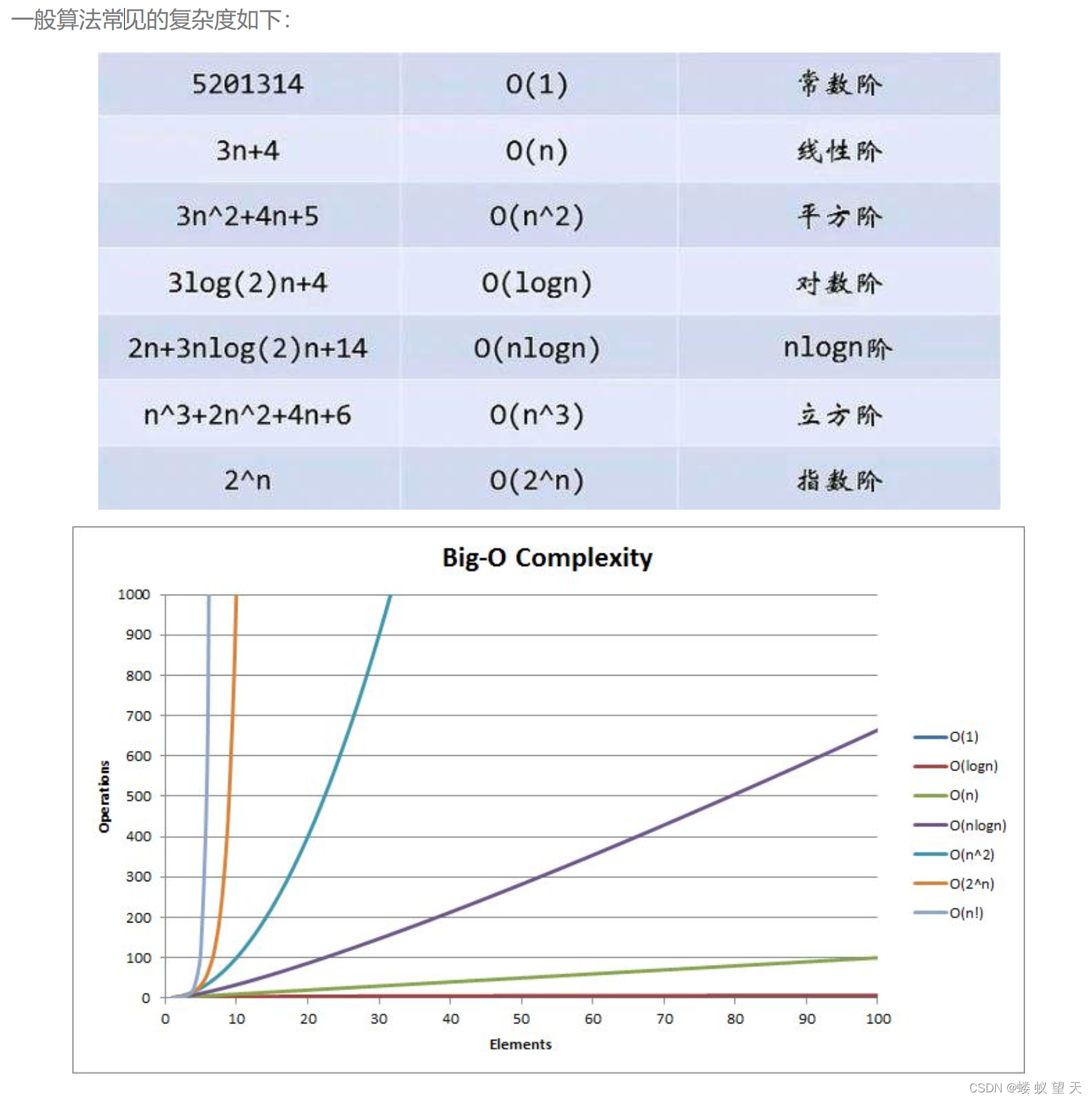
通过这张曲线图我们可以看到O（logn）的时间复杂度是秒杀其他算法的。
最后推荐大家做两道题：
链接:https://leetcode-cn.com/problems/missing-number-lcci/
链接: https://leetcode-cn.com/problems/rotate-array/
制作不易，期待你的三连，若有问题，欢迎私信指出。