比如：十进制的5，该数二进制为 0000 0101，将该数左移3为
结果为0010 1000，转换成十进制为 40，验证了上面的结论：5左移三位就等于5乘以2的三次方等于40。
再比如：十进制的40，右移三位就相当于除以8（2的三次方）结果为5。
那么问题来了，有一个数a，有一个数b，我要让b等于a的第三位，怎么算。

思路：先让a右移俩位，那么a原来的第三位现在就变成最后一位，再让移后的数和1想与，结果即为a原来的第三位。

一些面试常考的位操作运算


去掉最后一位 | (101101->10110) | 				x >> 1
在最后加一个0 | (101101->1011010) | 				x << 1
在最后加一个1 | (101101->1011011) |				x << 1+1
把最后一位变成1 | (101100->101101) | 			x | 1
把最后一位变成0 | (101101->101100) | 			x | 1-1
最后一位取反 | (101101->101100) | 				x ^ 1
把右数第k位变成1 | (101001->101101,k=3) | 		x | (1 << (k-1))
把右数第k位变成0 | (101101->101001,k=3) | 		x & ~ (1 << (k-1))
右数第k位取反 | (101001->101101,k=3) | 			x ^ (1 << (k-1))
取末三位 | (1101101->101) | 						x & 7
取末k位 | (1101101->1101,k=5) | 				x & ((1 << k)-1)
取右数第k位 | (1101101->1,k=4) | 				x >> (k-1) & 1
把末k位变成1 | (101001->101111,k=4) | 			x | (1 << k-1)
末k位取反 | (101001->100110,k=4) | 				x ^ (1 << k-1)
把右边连续的1变成0 | (100101111->100100000) | 	x & (x+1)
把右起第一个0变成1 | (100101111->100111111) | 	x | (x+1)
把右边连续的0变成1 | (11011000->11011111) |   	x | (x-1)
取右边连续的1 | (100101111->1111) | 				(x ^ (x+1)) >> 1
去掉右起第一个1的左边 | (100101000->1000) |   	x & (x ^ (x-1))
判断奇数 										(x&1)==1
判断偶数 										(x&1)==0 
取右边第一个1所在位置 							x&-x

获取二进制中最右边的1

x&(-x)
就是这么简洁，就能实现获取到二进制中最右边的 1，且其它位设置为 0。

原因：
首先在补码表示法中，负数的补码 = 取反 +1，这个都知道，但你可能没发现：
取反后：最右边的 0 的位置对应于最右边的 1 的位置，
而取反后 +1 ，则会把该位的1往前进位（同时该位也会恢复为0），直到遇到第一个0停止，并把此位置为1，而第一个0就恰恰对应第一个1。

所以负数的补码则相当于将最右边的 1 的左边的所有位取反。

如图

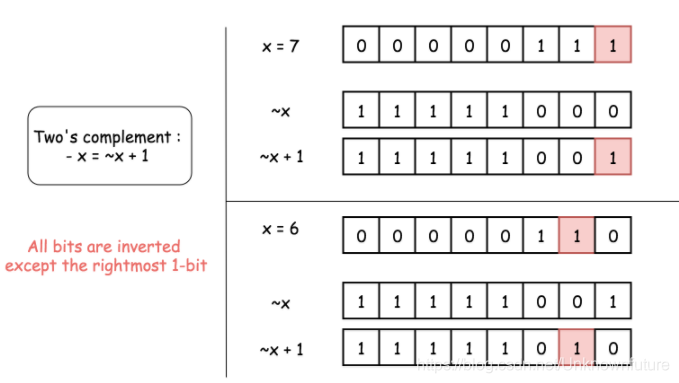
在这里插入图片描述
到这已经很显然了，x 和 −x 只有一个共同点：最右边的 1。
（其实这么说是不严谨的，因为最右边的1起，该位右边的0也是相同的，只是对操作没影响）

因此 x & (-x) 将保留最右边的 1。并将其他的位设置为 0。

计算机原码、反码、补码

机器数

一个数在计算机中的表现形式叫做机器数，这个数有正负之分，在计算机中用一个数的最高位（符号位）用来表示它的正负，其中0表示正数，1表示负数。

例如正数7，在计算机中用一个8位的二进制数来表示，是00000111，而负数-7，则用10000111表示，这里的00000111和10000111是机器数

“三码”之间的转换

注意：以下的分析均以 1字节 进行

	正数	负数
原码	数据的二进制形式	数据的二进制形式
反码	等于原码	原码的符号位不变，其他位取反
补码	等于原码	负数的反码“+1”

注意：无符号数，正数，它们的原码=反码=补码
负数：反码=原码的符号位不变，其他位取反
补码：反码+1.

重要：负数在计算机中存储的是补码。

计算机中为啥要用补码呢？

1，将减法运算变为加法运算：

就拿6-10==-4来举个例子：
如果没有补码，则计算如下：
6 + (-10) = -4
0000 0110
+1000 1010

--------------------
1001 0000 = -16 （则计算结果错误）

如果有补码：
0000 0110
1111 0110（- 10的补码）
-----------------
1111 1100（-4的补码）——>1000 0011——>1000 0100== -4
在上述补码的计算中我们也可以得出一个负数由补码到原码的计算方法：“原码 = 补码取反+1”

真数

计算机中的机器数对应的真实的值就是真数，对最高位（符号位）后面的二进制数转换成10进制，并根据最高位来确定这个数的正负。对于上面的00000111和10000111来说，对最高位后面的二进制数转换成10进制是7，在结合最高位的值，得出对应的真数分别是7和-7

原码

用第一位表示符号，其余位表示值。因为第一位是符号位，所以8位二进制数的取值范围就是：[1111_1111 , 0111_1111] 即 [-127 , 127] ,原码是容易被人脑所理解的表达方式

反码

正数的补码反码是其本身，负数的反码是符号位保持不变，其余位取反。例如正数1的原码是[0000_0001]，它的反码是是其本身

[0000_0001],-1的原码是[1000_0001],其反码是[1111_1110]

补码

正数的补码是其本身，负数的补码是在其反码的基础上+1，例如正数1的原码是[0000_0001],他的补码是其本身[0000_0001],

-1的补码是[1111_1111]

有了原码为什么要使用反码和补码

因为人脑可以知道第一位是符号位，可以根据符号位对真值的绝对值进行加减乘除，但是对于计算机来说，加减乘除是最最最基本的运算，要设计的尽量简单，计算机辨别符号位会让计算机的设计电路变得很复杂，于是人们想出了让符号位也参与到运算上来。减去一个数，等于加上他的负数。

使用原码参数运算的缺陷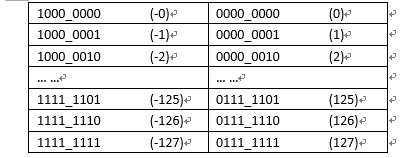
在这里插入图片描述

从上面的原码表中可以看见左边每增加一个二进制单位对应的真数是递减的，而右边每增加一个二进制单位对应的真数是递增的，所以对于原码来说，能满足正数的加法，但无法满足负数的加法

2+1 = [0000_0010]原+[0000_0001]原=[0000_0011]原 = 3

±1=[0000_00001]原+[1000_0001]原=[1000_0010]原=-2

为了满足负数对加法的需求，就必须让负数与他对应的二进制码是同步递增或者同步递减

于是就通过符号位不变，其余位取反来满足这个同步递增或者递减的要求，由于正数本来就满足它本身的加法，所以不需要做任何改变。这就是反码的定义由来。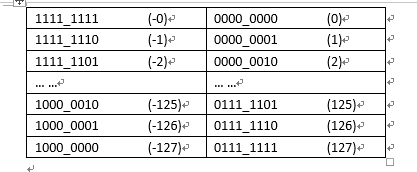
在这里插入图片描述

从上图的反码表中可以看到在运算不跨过0的时候，正负数的加法已经能满足要求

-2+1=[1111_1101]反+[0000_0001]反=[1111_1110]反=-1

127+1=[1000_0000]反=-127=128 加法算出来是128，由于128超过最大值，余1，所以取最小值开始的第一位，也就是

最小值-127，但是这里有个不合理的地方，就是[1111_1111]和[0000_0000]都表示0，这导致在实际计算中每当跨过0一次，就有一个单位的误差

-1+2=[1111_1110]反+[0000_0010]反=[0000_0000]反=0

要解决这个问题就必须让反码中的[1111_1111]和[0000_0000]合并，

由于[1111_1111]+[0000_0001]=[0000_0000],所以在负数反码的基础上+1就可以解决反码中跨0的误差问题，同时不会对负数与它对应的二进制反码的同步递增产生影响，所以在反码的基础上+1就完美的解决了符号参与预算的问题，这就是补码为什么是在负数反码的基础上+1的由来。

在这里插入图片描述

从上面的图中发现还有一个[1000_0000]的二进制没有对应任何真数，于是就规定了这个数的真数是-128

所以补码的表示范围是[-128~127] ，这样一来256个二进制正好表示256个整数，在实际二进制的运算中超过范围其实就是对256的取余预算（x+128）mod 256 - 128。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小小林熬夜学编程/article/detail/175766