时间序列预测的8种常用方法简介_时间序列预测方法

时间序列预测的7种方法

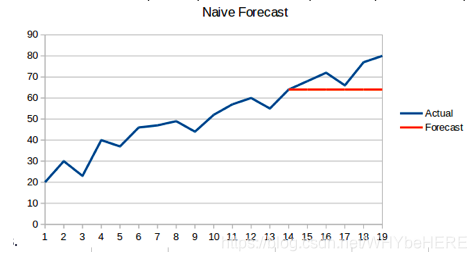
1. 朴素预测法（Naive Forecast)

如果数据集在一段时间内都很稳定，我们想预测第二天的价格，可以取前面一天的价格，预测第二天的值。这种假设第一个预测点和上一个观察点相等的预测方法就叫朴素法，即 $y_{t+1}=y_t$

2. 简单平均法(Simple Average）

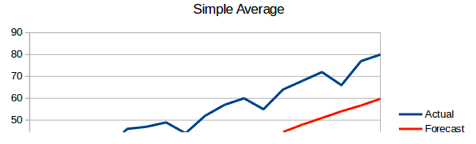
这种方法预测的期望值等于所有先前观测点的平均值，称为简单平均法。。

物品价格会随机上涨和下跌，平均价格会保持一致。我们经常会遇到一些数据集，虽然在一定时期内出现小幅变动，但每个时间段的平均值确实保持不变。这种情况下，我们可以认为第二天的价格大致和过去的平均价格值一致。这种将预期值等同于之前所有观测点的平均值的预测方法就叫简单平均法。即
$${\hat{y}}_{x+1}=1/x{\sum }_{i=1}^x{y}_i.$$
由图可见，这种方法并没有提高结果的准确度。因此，可以推断出，当每个时间段的平均值保持不变时，这种方法效果最好。

3. 移动平均法(Moving Average）

移动平均法也叫滑动平均法，取前面n个点的平均值作为预测值


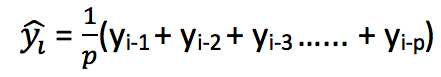
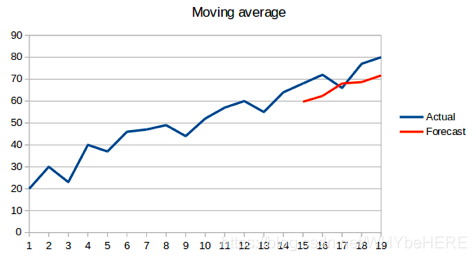
从图表中我们可以推断出，过去的观测值在这段时间里有很大幅度的上涨。如果使用简单平均法，我们必须使用所有历史数据的平均值，但是使用所有数据得出的结果并不正确。

因此，作为改进，我们只取最近几个时期的平均价格。显然，这里的想法是，只有最近的价值才重要。这种利用时间窗计算平均值的预测技术称为移动平均法。移动平均值的计算有时包括一个大小为n的“滑动窗口”。

计算移动平均值涉及到一个有时被称为“滑动窗口”的大小值p。使用简单的移动平均模型，我们可以根据之前数值的固定有限数p的平均值预测某个时序中的下一个值。这样，对于所有的 i>p

利用一个简单的移动平均模型，我们预测一个时间序列中的下一个值是基于先前值的固定有限个数“p”的平均值。因此，对于所有i>p

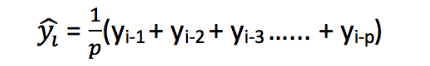
4. 加权移动平均(Weighted Moving Average)

加权移动平均法是对移动平均法的一个改进。在如上所述的移动平均法中，我们对过去的n个观测值进行了同等的加权。但我们可能会遇到这样的情况：过去“n”的每一个观察结果都会以不同的方式影响预测。这种对过去观测值进行不同加权的技术称为加权移动平均法。

加权移动平均法其实还是一种移动平均法，只是“滑动窗口期”内的值被赋予不同的权重，通常来讲，最近时间点的值越重要。即

这种方法并非选择一个窗口期的值，而是需要一列权重值（相加后为1）。例如，如果我们选择[0.40, 0.25, 0.20, 0.15]作为权值，我们会为最近的4个时间点分别赋给40%，25%，20%和15%的权重。

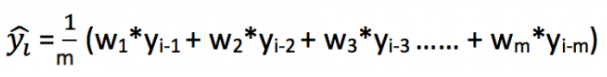
5. 简单指数平滑法 (Simple Exponential Smoothing)

我们注意到简单平均法和加权移动平均法在选取时间点的思路上存在较大的差异：简单平均法将过去数据一个不漏地全部加以同等利用；移动平均法则不考虑较远期的数据，并在加权移动平均法中给予近期更大的权重。我们就需要在这两种方法之间取一个折中的方法，在将所有数据考虑在内的同时也能给数据赋予不同非权重。

指数平滑法相比更早时期内的观测值，越近的观测值会被赋予更大的权重，而时间越久远的权重越小。它通过加权平均值计算出预测值，其中权重随着观测值从早期到晚期的变化呈指数级下降，最小的权重和最早的观测值相关：

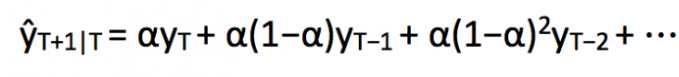
其中0≤α≤1是平滑参数。

对时间点T+1的预测值是时序y1,…,yT的所有观测值的加权平均数。权重下降的速率由参数α控制，
因此，它可以写为：

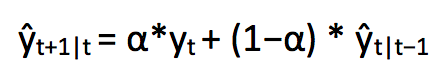
简单指数平滑法预测公式为：
$y_{t+1}^{\prime }=a{y}_t+(1-a)y{t}^{\prime }$ 式中，
$y_{t+1}^{\prime }$ : t+1期的预测值，即本期（t期）的平滑值St ；
$yt$: t期的实际值； 　
$y{t}^{\prime }$ : t期的预测值，即上期的平滑值St-1 。

该公式又可以写作：$y_{t+1}^{\prime }=y_t^{\prime }+a(y_t-y_t^{\prime })$。
可见，下期预测值又是本期预测值与以a为折扣的本期实际值与预测值误差之和。

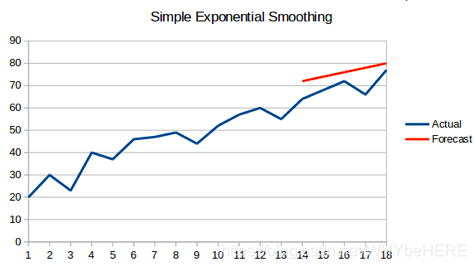
6. 霍尔特线性趋势法

Holts线性趋势模型，霍尔特线性趋势法，该方法考虑了数据集的趋势，即序列的增加或减少性质。

尽管这些方法中的每一种都可以应用趋势：简单平均法会假设最后两点之间的趋势保持不变，或者我们可以平均所有点之间的所有斜率以获得平均趋势，使用移动趋势平均值或应用指数平滑。

但我们需要一种无需任何假设就能准确绘制趋势图的方法。这种考虑数据集趋势的方法称为霍尔特线性趋势法，或者霍尔特指数平滑法。

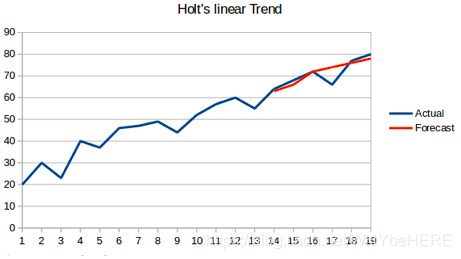
7. Holt-Winters方法（三次指数平滑）

霍尔特-温特（Holt-Winters）方法，有的地方也叫三次指数平滑法。Holt-Winters 方法在 Holt模型基础上引入了 Winters 周期项（也叫做季节项），可以用来处理月度数据（周期 12）、季度数据（周期 4）、星期数据（周期 7）等时间序列中的固定周期的波动行为。引入多个 Winters 项还可以处理多种周期并存的情况。

当一个序列在每个固定的时间间隔中都出现某种重复的模式，就称之具有季节性特征，而这样的一个时间间隔称为一个季节性特征。

例如酒店的预订量在周末较高，工作日较低，并且每年都在增加， 表明存在一个一周的季节性和增长趋势。

8. ARIMA

其他的预测方法，如自回归模型 AR§、移动平均模型 MA(q)、自回归移动平均模型 ARMA(p,q)、自回归差分移动平均模型 ARIMA(p,d,q), 可以说前三种都是 ARIMA(p,d,q)模型的特殊形式。

其中最经典的就是ARIMA模型：
ARIMA模型（英语：Autoregressive Integrated Moving Average model），差分整合移动平均自回归模型，又称整合移动平均自回归模型（移动也可称作滑动），是时间序列预测分析方法之一。ARIMA(p，d，q)中，AR是“自回归”，p为自回归项数；MA为“滑动平均”，q为滑动平均项数，d为使之成为平稳序列所做的差分次数（阶数）。“差分”一词虽未出现在ARIMA的英文名称中，却是关键步骤。

关于ARIMA的内容很多，后续会另外发表笔记总结相关知识，以及这几种方法的实例比较。

部分参考资料

Forecasting: Principles and Practice： https://otexts.com/fpp2/holt-winters.html
加权移动平均法：https://wiki.mbalib.com/wiki/%E7%A7%BB%E5%8A%A8%E5%B9%B3%E5%9D%87%E6%B3%95#.E4.B8.80.E3.80.81.E7.AE.80.E5.8D.95.E7.A7.BB.E5.8A.A8.E5.B9.B3.E5.9D.87.E6.B3.95
ARIMA模型百度百科： https://baike.baidu.com/item/ARIMA模型/10611682?fr=aladdin
趋势的预测：霍尔特指数平滑法 https://zhuanlan.zhihu.com/p/164919931)
指数平滑法 https://wiki.mbalib.com/wiki/指数平滑法
二次指数平滑法：https://wiki.mbalib.com/wiki/二次指数平滑法