项目实战——基于计算机视觉的物体位姿定位及机械臂抓取（双目标定）_机械手的机器视觉和位姿求解啥关系

项目实战——基于计算机视觉的物体位姿定位及机械臂抓取（双目标定）

        请各位读者朋友注意，这里面很多东西涉及到我的毕设，写作辛苦，请勿滥用，转载请务必注明出处！
        双目标定的目的是计算两个摄像机的相对位姿信息，并进行矫正，使得两台摄像机处于完全平行的状态。下面建立双摄像机模型，将相机相对位姿用数学表达式表达出来，并进行求解。

对极几何

        对极几何是双视图几何学理论的一部分，通常情况下，同一场景的两幅图像对应点之间存在着特殊的几何关系。这种关系仅取决于摄像机的内参数和两摄像机之间的相对位姿。
        1、极线约束
        对于单一的摄影机观测3D点w的情况，如图所示，w必定位于一条穿过光心和摄像机平面中$x_1$的光线上。

        但是，并不能确定该点位于这条射线上的具体位置（图纸标记了四个可能的位置）。现在考虑观测同一个3D点的第二个摄像机，从第一个摄像机可得，该点必定位于3D空间中的一条特定光线上，因此第二幅图像中该点的投影位置$x_2$必定唯一在第二幅图像中这条光线投影上的某个位置上。真实物理世界中的光线在二维平面中的投影称为极线。
        综上可以得出这样一个结论：对于第一幅图像中的任意点，它在第二幅图象中的对应点一定会在一条线上。这就是极线约束。该受约束的特定极线依赖于摄像机的内参数和外参数。
极线约束具有两个重要的实际意义：
        1) 在已知摄像机焦距、偏移量和相机间相对位姿的情况下，对于左视图中的二维像素点，只需在右摄像机拍摄图像中的极线进行一维搜索，即可得到该点在第二幅图像上的对应点位置。
        2) 对应点的约束是摄像机内在参数和外在参数的函数，已知摄像机内在参数的情况下，可利用对应点的观测模式来确定摄像机的外在参数，进而确定两台摄像机的相对位姿。
        2、极点
        在极线约束的基础上从另一个方面考量，第一幅图像中的每一个点都是物理世界中的一条光线的投影，而这些光线同时又在第二幅图像上投影形成极线。由于所有光线都聚集到摄像机1的光心，那么，所有光线在第二幅图像中形成的极线也将聚集于一点。该点即为摄像机1的光心在摄像机2中的对应点，也称极点。

        当然，极点并不一定在观测的图像内部，也有可能在图像之外的某一点上，下图描述了两种极端的情况：

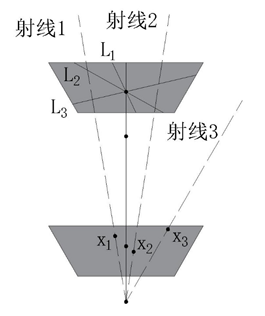
        当两台摄像机位于一条直线上时，极点位于图像中心，且极线呈放射状分布；当两台摄像机都位于同一方向且垂直于光轴，此时极线都是互相平行的，而极点位于无穷远处。
        以上即为对极几何的主要内容，它对于计算摄像机相对位姿信息（求解摄像机外参数），进行立体匹配（寻找对应点）具有重要的作用。

基础矩阵与实矩阵

        为了研究方便，在研究双摄像机时，假定第一个摄像机为世界坐标的坐标中心，因此第一个摄像机的外在参数为：{I,0}。第二个摄像机处于任意位置。这样，在齐次坐标中，一个3D点投影到两个摄像机上，可表示为：

${\lambda }_1{\overline{x}}_1={\Lambda }_1[1,0]\overline{w}={\Lambda }_1\overline{w}$
${\lambda }_2{x}_2={\Lambda }_2[\Omega ,\tau ]\overline{w}={\Lambda }_2\Omega \overline{\omega }+{\Lambda }_2\tau$

        将上面两个公式合并，可得：

${\lambda }_2{\overline{x}}_2={\lambda }_1{\Lambda }_2\Omega {\Lambda }_1^{-1}{\overline{x}}_1+{\Lambda }_2\tau$

        使用平移向量τ乘以两边求它们的向量外积，可将${\Lambda }_2\tau$这一项约去：

${\lambda }_2\tau \times {\overline{x}}_2={\lambda }_1\tau \times ({\Lambda }_2\Omega {\Lambda }_1^{-1}{\overline{x}}_1)$

        使用${\overline{x}}_2$乘以两边求它们的向量内积，可将等式左边约去：

$x_2^T{\Lambda }_2^{-T}\tau \times \Omega {\Lambda }_1^{-1}{\overline{x}}_1=0$

        其中外积算子$\tau \times$可以表达为一个秩为2的非对称3x3的矩阵${\tau }_{\times }$：

${\tau }_{\times }=\left[\begin{array}{ccc}0& -{\tau }_z& {\tau }_y\\ -{\tau }_z& 0& -{\tau }_x\\ -{\tau }_y& {\tau }_x& 0\end{array}\right]$

        因此，令$F={\Lambda }_2^{-T}\tau \times \Omega {\Lambda }_1^{-1}$，则：$x_2^{T}F{\overline{x}}_1=0$可以看作是摄像机2中的点向摄像机1中点的对应。
        令$E=\tau \times \Omega$，则：$F={\Lambda }_2^{-T}E{\Lambda }_1^{-1}$。其中${\Lambda }_1$，${\Lambda }_2$是两台摄像机的内参数，E实际上就是两摄像机间的位姿变换矩阵。称F为基础矩阵，E为实矩阵（本征矩阵）。因此，通过对两部摄像机的标定，得到${\Lambda }_1$，${\Lambda }_2$后，只要求解出基础矩阵，就能知道实矩阵，也就找到了两个相机位姿对应信息，即：

$E={\Lambda }_2^{T}F{\Lambda }_1$

实矩阵与对极几何

        由$E=\tau \times \Omega$，可知实矩阵E时一个3×3的矩阵，储存的是两个摄像机间的几何关系信息。由于外积算子${\tau }_{\times }$的秩为2，因此$det[E]=0$。同时实矩阵只依赖于两个摄像机之间的旋转和平移，每个摄像机由 3个参数，所以一般认为实矩阵具有6个自由度（也可以认为：第一个摄像机位于世界坐标的坐标中心，自由度可略去不计，第二个摄像机在空间中具有位置和方向的六个自由度，因此加起来共6个自由度）。
        由于矩阵比未知量具有较少的自由度，因此矩阵的3×3共9个项必须服从一组代数约束，可以简单地表示为：

$2E{E}^{T}E-trace[E{E}^T]E=0（2-71）$

        矩阵获取极线信息。极线上的点可以表示为：

$ax+by+c=0$

        写成矩阵形式可表示为：

$\left[\begin{array}{ccc}a& b& c\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=0$
$l\overline{x}=0$

        根据实矩阵的定义，不难有：

${\overline{x}}_2^{T}E{\overline{x}}_1=0$

        其中${\overline{x}}_2^{T}E$ 是一个1×3的向量，所以该关系可表示为$l_1{\overline{x}}_1=0$。不难推断：
$l_1={\overline{x}}_2^{T}E$是点$x_2$在图像1中对应的极线。同样地，也可以得出$x_1$在图像2中对应的极线：

$l_1={\overline{x}}_2^{T}E$
$l_2={\overline{x}}_1^T{E}^T$

        即为实矩阵与极线的对应关系。当然极点信息也可以通过实矩阵获得，设左右两个摄像机的两个极点用${\overline{e}}_1$和${\overline{e}}_2$表示。第一幅图像中每条极线均通过极点${\overline{e}}_1$，因此有：

$l_1{\overline{e}}_1={\overline{x}}_2^{T}E{\overline{e}}_1=0$

        根据矩阵知识，${\overline{e}}_1$一定位于E的右零空间，同理${\overline{e}}_2$也必定位于E的左零空间，即：

${\overline{e}}_1=null[E]$
${\overline{e}}_2=null[E^T]$

        可以对E进行SVD分解，$E=UL{V}^T$，令${\overline{e}}_1$等于V的最后一列，${\overline{e}}_2$为U的最后一行，以此来求解极点信息。
        总结一下，实矩阵与极点、极线的关系可以用以下公式表示:

$l_1={\overline{x}}_2^{T}E$
$l_2={\overline{x}}_1^T{E}^T$
${\overline{e}}_1=null[E]$
${\overline{e}}_2=null[E^T])$

矩阵求解（8点算法）

        由双摄像机模型，得到了摄像机2中的点向摄像机1中点的对应关系：$x_2^{T}F{\overline{x}}_1=0$，由于$x_2^T$为1x3的矩阵，${\overline{x}}_1$为3x1的矩阵，因此F为3x3的矩阵。将表达式展开写，在齐次坐标中，图像1中第i个点与图像2中第i个点的对应关系为：

$\left[\begin{array}{ccc}{x}_{i2}& y_{i2}& 1\end{array}\right]\left[\begin{array}{ccc}{f}_{11}& f_{12}& f_{13}\\ f_{21}& f_{22}& f_{23}\\ f_{31}& f_{32}& f_{33}\end{array}\right]\left[\begin{array}{c}{x}_{i}1\\ y_{i}1\\ 1\end{array}\right]=0$

        继续展开，可写为：

$x_{i2}{x}_{i1}{f}_{11}+x_{i2}{y}_{i1}{f}_{12}+x_{i2}{f}_{13}+y_{i2}{x}_{i1}{f}_{21}+y_{i2}{y}_{i1}{f}_{22}+y_{i2}{f}_{23}{x}_{i1}{f}_{31}+y_{i1}{f}_{32}+f_{33}=0$

        将上式用向量内积的形式表达：

$[x_{i2}{x}_{i1},x_{i2}{y}_{i1},x_{i2},y_{i2}{x}_{i1},y_{i2}{y}_{i1},y_{i2},x_{i1},y_{i1},1]f=0$

        其中：$f=[f_{11},f_{12},f_{13},f_{21},f_{22},f_{23},f_{31},f_{32}{f}_{33}]$即为基础矩阵F的矢量形式。这样就为F中的元素增加了一个线性约束，因此，对于I个已知的匹配点，可以得到：

$\left[\begin{array}{ccccccccccccc}{x}_{12}& x_{11}& x_{12}& y_{11}& x_{12}& y_{12}& x_{11}& y_{12}& y_{11}& y_{12}& x_{11}& y_{11}& 1\\ x_{22}& x_{21}& x_{22}& y_{21}& x_{22}& y_{22}& x_{21}& y_{22}& y_{21}& y_{22}& x_{21}& y_{21}& 1\\ .& .& .& .& .& .& .& .& .& .& .& .& .\\ .& .& .& .& .& .& .& .& .& .& .& .& .\\ .& .& .& .& .& .& .& .& .& .& .& .& .\\ x_{I2}& x_{I1}& x_{I2}& y_{I1}& x_{I2}& y_{I2}& x_{I1}& y_{I2}& y_{I1}& y_{I2}& x_{I1}& y_{I1}& 1\end{array}\right]f=0$
$|f|=1$

        需要说明的是，观察上述公式，F可以看作是一个常数，因此在其中增加了范数为1的约束。对于f中的9个参数，至少需要$I=8$对点。以上即为求解摄像机对应矩阵的方法，由于用到了8个对应点信息，所以该算法也称8点算法。
        该算法求解过程较为简单，但以上考虑的因素只是理想中的情况，在实际情况下会存在各种各样的误差，如：数据噪声、匹配点匹配错误、数据的误差，只要有任意一点误差，就足以对计算结果产生严重影响，进而影响到整个双目测距结果。换句话说，该算法的鲁棒性很差，因此在8点算法的步骤上提出了很多修正算法，以减少误差。
        1、图像坐标归一化处理
设八点算法等式左边的系数矩阵为A，以上公式可表示为：

$Af=0$

        造成八点算法不稳定的原因主要在于系数矩阵A， A直接使用的是原图像的像素坐标，没有经过任何处理，而每个像素点坐标分量的数量级相差太大，这就造成了矩阵A的不稳定。因此，在带入矩阵进行计算之前，首先要对像素坐标进行归一化处理，这样就可以消除数量级不同引起的巨大误差，提高矩阵A的稳定性。处理方法主要是对原始图像坐标进行同向性变换。
        归一化处理主要分为两步：
        1、变换选定像素点的位移，使得像素点集与原图像的原点重合；
        2、对图像点进行放缩变换，使他们到原点的平均距离为√2。

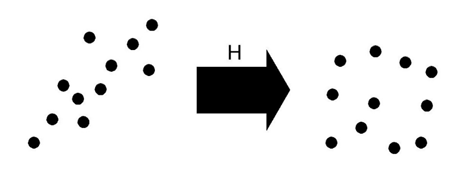
        上图形象地描述了归一化处理的过程：左侧为原始图像点，右侧为处理后的点，其中H为归一化变换的矩阵，可表示为：

$H=\left[\begin{array}{ccc}{k}_m& 0& -k_m{u}_0\\ 0& k_m& -k_m{v}_0\\ 0& 0& 1\end{array}\right]$
$u_0=1/N{\sum }_{i=1}^N{u}_i$
$v_0=1/N{\sum }_{i=1}^N{v}_i$

        ${\sigma }_m$表示尺度，其表达式为：

${\sigma }_m=\surd (({\sum }_{(}i=1{)}^N[(u_i-u_0{)}^2+(v_i-v_0{)}^2])/N)$
$k_m=\surd 2/{\sigma }_m$

        至此，改进后的八点算法步骤如下:
        (1)、对两幅图像分别进行归一化处理：${\overline{p}}_l=H{p}_i$，${\overline{p}}_l^{\prime }=H^{\prime }{p}_i^{\prime }$。
        (2)、根据八点算法，重新计算基础矩阵$\overline{F}$。
        (3)、进行反归一化根据变换$F=H_2^T\overline{F}{H}_1$，还原基础矩阵F。
        2、最小二乘法处理
        这里采用的最小二乘法处理类似于单目标定中对摄像机内参的求解。虽然八点算法要求的时至少有八个对应点，但在实际计算的过程中，匹配点的数量远超八个，显然，此时$Af=0$成为一个超定方程。根据单目标定中的经验，此时方程已然无解，转而求解方程的最小二乘解。
        这样由I个已知匹配点，组成矩阵$A_{I\times 9}$，采用最小二乘法求解的约束目标可表示为：

$mi{n}^{\Vert f\Vert =1}\Vert Af{\Vert }^2$

        其中A的每一行表示一个匹配点对应的系数，$f9x1$为基础矩阵F的求解向量，根据范数的定义：

$\Vert Af{\Vert }^2=(Af{)}^T(Af)=f^T(A^{T}A)f$

        令$M=A^{T}A$，M是一个9x9的向量，根据最小二乘求解的结论，采用奇异值分解法，分解矩阵A：

$A=US{V}^T$

        最小二乘解就是$V^T$的第九个列向量，即:$f=V^T$。
        另外还可以根据基础矩阵F的一个重要性质对最小二乘解进行优化，即：
$Rank(F)=2$
        由于噪声等因素的影响，通常情况下$Rank(F)>2$，因此这里选取前两个特征值在信息损失最小的情况下近似代替：

$F=SVD=S\left[\begin{array}{ccc}{v}_1& 0& 0\\ 0& v_2& 0\\ 0& 0& v_3\end{array}\right]D$

        令$v_3=0$，即

：
$F=SVD=S\left[\begin{array}{ccc}{v}_1& 0& 0\\ 0& v_2& 0\\ 0& 0& 0\end{array}\right]D$

        上述求得的F即为最终得到的基础矩阵。
        3、随机采样一致性（RANdom SAmple Consensus，RANSAC）
        通过两个摄像机的图像估计基础矩阵，唯一的输入来源就是匹配好的对应的点。在实际计算时，匹配点一定会存在误差，这种误差一般有以下两种情况:
        (1)测量点位置不精确引起的系统误差，这种误差服从高斯分布。
        (2)匹配点错误（错误的匹配点也称外点）引起的误差，这种误差不服从高斯分布。
        在计算的过程中，错误的匹配点能够造成极大的误差。对于外点，即使只有一组，也会造成很大的影响。因此，需要通过一种方法剔除外点，筛选出正确的匹配点（也称内点）。这种方法就是随机采样一致性（RANSAC）。
        该方法适用于外点较多时的情况（当外点较少时，可以采用最小二乘法来确定）。它的基本假设主要有两条：
        (1)数据中包含有内点，且内点数据符合某种数学分布；
        (2)外点并不符合内点的数学分布，一般是无规律的，其产生原因主要有：数据噪声、计算错误、测量错误等；
        下面给出RANSAC的算法：
        Step1：假设共有N个数据组成的集合P，集合P包含了内点和外点，并至少可以通过n个点拟合出模型；
        Step2：从集合P中随机选取n个点构成集合p；
        Step3：根据集合p估计出数学模型M；
        Step4：对剩余N-n个点分别判断是否适用模型M，适用的为内点，否则为外点，并统计内点的个数m_i。
        Step5：重复Step2~Step4步骤k次，并选取m_i最大（即:内点最多）的情况作为最终结果。
        该算法的核心是对于k值的选取。k值过小，则会对内点、外点估计错误；k值过大，则会增加计算工作量。实际上，可以通过理论计算来推断k值。Step2每次从集合P中选取n个点，假设选取到内点的概率为ϖ，则:
$\varpi =内点数目/数据集数目$
        那么所有的选取点均为内点的概率为${\varpi }^n$，所有的选取点均不是内点的概率为$1-{\varpi }^n$，${1-{\varpi }^n}^k$是k次选取均没有选到内点的概率。设p为k次迭代中至少有一次选择的点均为内点的概率，则1-p表示k次迭代均没有选到内点。因此数值上等于${1-{\varpi }^n}^k$，即：

$1-p={1-{\varpi }^n}^k$

        两边取对数则有：

$k=log(1-p)/log（1-{\varpi }^n)$

        一般取p≥95%，由此可以选取k值。另外需要注意的是：以上计算的一个重要的前提是，n个点的选取是独立随机的，也就是说，被选到的点在后续迭代过程中仍有可能被选到。而由此估计出的k值一般认为是选取不重复点的最大迭代次数。
        为了计算出更可靠的参数，k值计算出后一般会叠加一个标准偏差，k的标准偏差定义为：

$SD(k)=\surd (1-{\omega }^n)/{\omega }^n$

        除了k值的选取，还有一点需要考虑：用于判定是否符合模型M的判定依据。这里用点到另一幅图像上匹配点与预测极线之间的平方距离来表示。对于二维点x=[x,y]^T，与极线l=[a,b,c]，定义它们的距离为：

$dist[x,l]=(ax+by+c)/\surd (a^2+b^2)$

        综上，利用RANSAC方法估算基础矩阵的步骤为:
        Step1：从匹配点中选取8个点，计算基础矩阵$F_i$;
        Step2：计算其余点到极线的距离$dist[x,l]$，如果$dist[x,l]<d$（d是设定好的阈值），则为内点，否则为外点。并统计外点个数$m_i$；
        Step3：迭代k次，直到得到内点个数大于95%时即停止。此时选取$m_i$的最大值的情况作为最终结果。
        综合以上1、2、3点，总结一下求解两个摄像机对应矩阵的步骤。
        Step1：对两颗摄像头分别进行单目标定，求得相机的内在参数${\Lambda }_1$，${\Lambda }_2$；
        Step2：通过半块全局匹配算法（后续会详细说明）取得两幅对应图像中的匹配点；
        Step3：在Step2的匹配点中随机选取八个点，进行归一化处理；
        Step4：根据匹配点确定系数矩阵A；
        Step5：对A进行奇异值分解：$A=US{V}^T$，则f的解为：$f=V^T$；
        Step6：对求得的矩阵$\overline{F}$，进行SVD分解：$\overline{F}=S\times diag(v_1{v}_2{v}_3)V^T$，并令$v_3=0$得到基础矩阵的估计$F_i=S\times diag(v_1{v}_{2}0)V^T$
        Step7：分别计算其他匹配点到极线的距离，如果$dist[x,l]<d$则为外点，否则为内点。并统计外点个数$m_i$；
        Step8：返回Step3并执行Step3~7，迭代k次，直到得到内点个数大于95%时即停止。此时选取m_i的最大值的基础矩阵值F ̅作为最终结果。
        Step9：根据公式$E={\Lambda }_2^{T}F{\Lambda }_1$，代入${\Lambda }_1$，${\Lambda }_2$，F得到实矩阵，即：两台相机的转换矩阵。

立体矫正

        通过计算出本征矩阵，并得到摄像机的相机转换矩阵后，根据2.1的基本原理，通过两个摄像机计算视深的前提是两个摄像机必须保证绝对的平行。因此下一步任务就是：使得两个摄像机的光轴完全平行，将摄像机所拍摄图像转换成完全平行摄像机所拍摄的图像。这一步也称为立体校正。
        在上图中，由于极线是相互平行的，因此三维世界的点在左右像面成的像高度是一致的。后面在进行立体匹配时，只需要在同一行上进行搜索即可，这样匹配效率就会大大提高。
本文采用Bouguet算法对图像进行立体校正，该算法的效果是：使左右视图中每幅图像的重投影畸变最小化，同时使视图的公共视野最大化。主要思路是：将旋转矩阵R在两个摄像机之间分为两半（如果单纯旋转右侧摄像机与左侧平行，或者旋转左侧摄像机与右侧平行，那么它们的光轴方向就会发生很大的偏移，会使图像重投影畸变较大，因此折中的方法就是两侧都旋转一半，这样就可以最小化图像重投影畸变）。这里分别将左右摄像机的合成旋转矩阵称为$r_l$,$r_r$。将每个摄像机旋转二分之一，则它们的光轴最终平行于原始光轴所指的矢量和。需要注意的是，这样做会将两个摄像机设置为共面而非行对准。
        定义矩阵$R_{r}ect$为左摄像机的变换矩阵，目的是将其极线变为水平，且极点移至无穷远处。为了计算该矩阵，设图像主点$(c_x,c_y)$为原极点方向，则归一化后的极点方向为两台摄像机投影中心之间的平移矢量方向，这里构造一个由极点$(e_1)⃗$方向开始的旋转矩阵：

$(e_1)⃗=T⃗/\Vert T⃗\Vert ={\left[\begin{array}{ccc}(T_x& T_y& T_z\end{array}\right]}^T/\Vert T⃗\Vert$

        下一个矢量$e_2$必须和$e_1$正交，否则不受约束。对于$e_2$，选择一个正交于主光线的方向（趋于沿像平面）是一个不错的选择。通过使用$e_1$与主光线方向的叉乘乘积来实现，然后归一化即可获得另一个单位矢量。

$(e_2)⃗=1/\surd (T_x^2+T_y^2)((-T_y{T}_{x}0){)}^T$

        由于第三个矢量方向$e_3$与$e_1$和$e_2$垂直，因此：

$(e_3)=(e_1)\times (e_2)$

        由此可以得到矩阵$R_{r}ect$为：

$R_{r}ect=\left[\begin{array}{c}(e_1{)}^T\\ (e_2{)}^T\\ (e_3{)}^T\end{array}\right]$

        该矩阵将左侧摄像机围绕投影中心旋转，左右摄像机通过R_rect与合成旋转矩阵的乘积实现对准：

$R_l=R_{rect}\bullet r_l$
$R_r=R_{rect}\bullet r_r$

        同样，可以计算标定的左右摄像机矩阵${\Lambda }_{(}rect,l)$与${\Lambda }_{(}rect,r)$，且它们返回与投影矩阵$p_l^{\prime }$与$p_r^{\prime }$结合:

$p_l={\Lambda }_{(}rect,l)\bullet p_l^{\prime }=\left[\begin{array}{ccc}{\phi }_x& \gamma & {\delta }_x\\ 0& {\phi }_y& {\delta }_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right]$

$p_l={\Lambda }_{(}rect,r)\bullet p_l^{\prime }=\left[\begin{array}{ccc}{\phi }_x& \gamma & {\delta }_x\\ 0& {\phi }_y& {\delta }_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& T_x\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right]$

        投影矩阵通过以下步骤将单应坐标系中的一个三维点转换到一个二维单应坐标系：

$P\bullet \left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]$

        另外可以根据$(x,y)=(x⁄w,y∕w)$来计算图像坐标。当然也可以将图像中的点还原到真实物理世界中，重投影矩阵为：

$Q=\left[\begin{array}{cccc}1& 0& 0& -{\delta }_x\\ 0& 1& 0& -{\delta }_y\\ 0& 0& 1& f\\ 0& 0& -1/T_x& ({\delta }_x-{\delta }_x^{\prime })/T_x\end{array}\right]$

        矩阵Q中的参数来源于左摄像机，但${\delta }_x^{\prime }$是右侧视图中x坐标轴主点，如果两个相机完全平行，则${\delta }_x^{\prime }={\delta }_x$，即$Q(4,4)=0$。因此，重投影关系可表示为：

$Q\bullet \left[\begin{array}{c}x\\ y\\ d\\ 1\end{array}\right]=\left[\begin{array}{c}X\\ Y\\ Z\\ W\end{array}\right]$

        式中，d表示偏差，三维世界坐标即为： [ X / W Y / W Z / W ] T \left[

$$\begin{matrix}X/W &Y/W &Z/W\end{matrix}$$ \right]^T [X/W​Y/W​Z/W​]T

OpenCV双目标定

        上面详细阐述了双目标定的具体算法，下面详细阐述其具体操作方法。
        OpenCV提供了双目标定的实现。本文采用的C++语言开发，IDE为VS2015，OpenCV版本为4.0版本。以下介绍其主要实现函数：
        1、双目标定
        double cv :: stereoCalibrate （
        InputArrayOfArrays objectPoints，
        InputArrayOfArrays imagePoints1，
        InputArrayOfArrays imagePoints2，
        InputOutputArray cameraMatrix1，
        InputOutputArray distCoeffs1，
        InputOutputArray cameraMatrix2，
        InputOutputArray distCoeffs2，
        Size imageSize，
        OutputArray R，
        OutputArray T，
        OutputArray E，
        OutputArray F，
        INT flags = CALIB_FIX_INTRINSIC，
        TermCriteria standard =TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 1e-6)
        /*
        objectPoints 储存标定角点在世界坐标系中的位置；
        imagePoints1、imagePoints2 摄像机1、2的棋盘角点像素坐标；
        cameraMatrix1 左摄像机的内参矩阵；
        distCoeffs1 左摄像机的畸变系数矩阵；
        cameraMatrix2 右摄像机的内参矩阵；
        distCoeffs2 右摄像机的畸变系数矩阵；
        imageSize 图像的大小；
        R，左右摄像机的旋转矩阵；
        T，左右摄像机的平移矩阵；
        E，本征矩阵；
        F，基本矩阵；
        Flag 可能为零的不同标志或以下值的组合：
        CV_CALIB_FIX_INTRINSIC固定输入的cameraMatrix和distCoeffs不变，这样只估算R，T，E和F矩阵。
        CV_CALIB_USE_INTRINSIC_GUESS以单目标定的相机内参和畸变系数为初始值进行迭代。
        CV_CALIB_FIX_PRINCIPAL_POINT 不改变图像原点。
        CV_CALIB_FIX_FOCAL_LENGTH迭代过程中不会改变焦距
        CV_CALIB_ZERO_TANGENT_DIST不考虑两台摄像机的切向畸变系数。
        CALIB_THIN_PRISM_MODEL计算系数s1，s2，s3和s4。
        CALIB_TILTED_MODEL系数tauX和tauY已启用。
        /
        2、根据观察到的点坐标计算理想点坐标
        void cv :: undistortPoints （
        InputArray src，
        OutputArray dst，
        InputArray cameraMatrix，
        InputArray distcoeffs，
        InputArray R = noArray()，
        InputArray P =noArray()
        ）
        /
        src， 观察到的点坐标
        dst，在非畸变和反向透视变换后输出理想点坐标。
        cameraMatrix 相机内参矩阵
        distCoeffs 相机畸变矩阵
        R - 对象空间中的整流变换（3x3矩阵），如果矩阵为空，则使用身份转换。
        P - 新的相机内参矩阵。
        /
        3、极线计算
        void cv :: computeCorrespondEpilines （
        InputArray points，
        // 输入矩阵。
        //包含点的图像索引（1或2）
        InputArray F，
        //基本矩阵
        OutputArray line
        //输出的极线参数矩阵
         ）;
        4、基本矩阵计算
        Mat cv :: findFundamentalMat（
        InputArray points1，
        //第一幅图像的阵列点。
        InputArray points2，
        //与points1相同。
        Int method = FM_RANSAC，
        //用于计算基本矩阵的方法。
        /
        CV_FM_7POINT用于7点算法。ñ= 7
        CV_FM_8POINT通用的8点算法。ñ≥ 8
        用于RANSAC算法的        CV_FM_RANSAC。ñ≥ 8
        CV_FM_LMEDS为LMedS算法。ñ≥ 8
        /
        double param1 = 3.0，
        //用于随机一致性采样的参数。用于判断是否为噪点的阈值
        double param2 = 0.99，
        //用于随机一致性采样和LM算法的参数，表示置信水平
        OutputArray mask =noArray()
        ）
        5、计算校准立体相机的每个摄像机的校正变换
        void cv :: stereoRectify （
        InputArray cameraMatrix1，
        InputArray distCoeffs1，
        InputArray cameraMatrix2，
        InputArray distCoeffs2，
        Size imageSize，
        InputArray R，
        InputArray T，
        OutputArray R1，
        OutputArray R2，
        OutputArray P1，
        OutputArray P2，
        OutputArray Q：
        Int flags = CALIB_ZERO_DISPARITY，
        double alpha = -1，
        Size newImageSize = Size()，
        Rect * validPixROI1 = 0，
        Rect * validPixROI2 =0
        ）
        /
        cameraMatrix1– 第一个相机矩阵.
        distCoeffs1– 第一个相机畸变参数.
        cameraMatrix2
        distCoeffs2
        imageSize– 用于校正的图像大小；
        R–旋转矩阵；
        T– 平移矩阵；
        R1、R2–矫正旋转矩阵；
        P1、P2–投影矩阵（3x4）；
        Q–输出深度视差映射矩阵
        Flags-操作标志一般设为CV_CALIB_ZERO_DISPARITY，也可设置为0。
        Alpha-自由缩放参数。
        validPixROI1/ validPixROI2 -如果选择，则会输出矩形。
        /
        6、计算无畸变和裁剪后的转换图
        void cv :: initUndistortRectifyMap（
        InputArray cameraMatrix，
        InputArray distcoeffs，
        InputArray R，
        InputArray newCameraMatrix，
        Size size，
        Int m1type，
        OutputArray map1，
        OutputArray map2
        ）
        /
         cameraMatrix——摄像机内参矩阵
         distCoeffs——摄像机畸变系数矩阵
         R——两台摄像机之间的旋转矩阵
         newCameraMatrix——校正后的摄像机内参矩阵
         size——摄像机采集的无畸变图像尺寸
        m1type——map1的数据类型
        map1——输出的X坐标重映射参数
        map2——输出的Y坐标重映射参数
        */
        在本文程序中，双目标定写成了一个单独的.c文件，名称为StereoCalib，其主函数为：
        result *StereoCalib(
        int board_w, //棋盘的宽度
        int board_h, //棋盘的高度
        cv::Mat M1,
        cv::Mat D1,
         cv::Mat M2,
         cv::Mat D2,
         const char *imageList, //图像文件列表
        bool useUncalibrated, //是否使用未校准方法
        bool displayCorners, //是否显示角点
         bool showUndistores, //是否显示校正后的图像
         bool isVerticalStereo //判断图像是垂直还是水平
        )
        双目标定利用的是单目标定时所拍摄的图像，即:在单目标定时，当检测到棋盘图案时，左摄像机和右摄像机同时拍摄。经过双目标定，校正并对应后的图像如图所示:

        图像中包括左右摄像机拍摄棋盘图像经过单目标定、双目标定、裁剪后的对应图案，图中绿线即为极线（极点位于无穷远处），重映射平均误差为1.75537。
        经过计算，双目相机的R、T、E、F四个参数分别为：
        旋转矩阵（R）：

$\left[\begin{array}{ccc}0.9981761553222738& 0.008033309321453018& -0.05983167127258031\\ -0.00426022359904628& 0.9980092129495719& 0.06292425099007747\\ 0.06021804912922742& -0.06255459063187922& 0.9962232228521618\end{array}\right]$

        平移矩阵（T）：

$\left[\begin{array}{c}10.43727100758126\\ -10.19376973116046\\ -4.541974218262003\end{array}\right]$

        本征矩阵（E）：

$\left[\begin{array}{ccc}-0.6331987522339517& 5.170599207333293& -9.869469808889111\\ -5.162202461067245& 0.6164121313678637& -10.1260978525939\\ 10.13071277023418& 10.49838232901963& 0.04684718093913587\end{array}\right]$

        基本矩阵（F）：

$\left[\begin{array}{ccc}-1.629360687398105e^{-7}& 1.516148714271131e^{-6}& 0.02439611694235628\\ -1.513686578734253e^{-6}& 2.05965718081223e^{-7}& -0.0280764078560412\\ 0.02513265792029904& 0.02909431391207914& 1\end{array}\right]$

        Hunt Tiger Tonight
        2019-10-29
        联系方式：18398621916@163.com（请勿使用其他联系方式，谢谢！）
        PS:再次请各位读者朋友注意，这里面很多东西涉及到我的毕设，写作辛苦，请勿滥用，转载请务必注明出处！