浮点数的存储方式，取值范围和舍入模式_浮点数尾数舍入

作者：小小林熬夜学编程 | 2024-04-17 05:48:17

踩

浮点数尾数舍入

浮点数的存储方式

IEEE754提供了二进制存储十进制浮点数的具体标准，分别为单精度型，双精度型，延伸单精度型，延伸双精度型。

一单精度类型(float)

符号位S：31位，0代表正，1代表负

指数位E：23-30位

尾数位F：0-22位

一个十进制浮点数可以表示为：

规范化

尾数的小数点放在第一位和第二位之间，且保证第一位不为0，故尾数始终表示为1.****，这个处理过程称为规范化(normailzed)。

规范化之后，尾数始终表示为1.****，存储尾数时，省略前面的1，只记录小数点之后的部分，不够23位的在低位补0。

IEEE754规定，单精度浮点数的指数位用于表示[-127, 128]范围内的指数（双精度的偏移量为1023），浮点型的指数位都有一个固定的偏移量(bias)，指数 + 偏移量 = 非负整数。因此实际计算需要减去这个偏移量B。

现在一个十进制数可以表示为：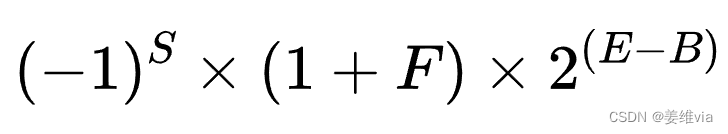

规格数和非规格数

根据IEEE754的规定, 按照尾数位隐藏的整数部分是 1. 还是0. 可以将浮点数划分为两类: normal number(规格数) 和 subnormal number(非规格数)

尾数位隐藏的整数部分为1.的数称为规格数，大部分数都为规格数，存储尾数时，省略前面的1，只存储小数点之后的部分；

尾数位隐藏的整数部分为0.的数称为非规格数，为了表示subnormal number, IEEE754规定: 如果将指数位全部填充为0, 则表示这个数是个非规格数。

特殊数

特殊数分为两种: 无穷（infinity）和NaN（not a number)

无穷

当指数位全为1，且尾数位全为0时，就表示为无穷，根据符号位来确定是正无穷还是负无穷，分别记做+infinity和-infinity，由于浮点数有其取值范围，超过范围就被记作无穷，关于浮点数的取值范围下面再说。

NAN

当指数位全为1，且尾数位不全为0，就表示为NaN，NaN没有+/-之分，统称NaN。

二双精度类型(double float)

存储双精度浮点数需要64个比特位，其中最高位仍是符号位S，而指数位E提升到了11位，尾数位F提升到了52位。

这里有个可以方便实现十进制数到32位浮点数转换的网站网站https://www.h-schmidt.net/FloatConverter/IEEE754.html可惜该网站暂时不能计算双精度64位，不过借助ChatGPT可以方便的写一段代码帮助查看，借助菜鸟的c在线编译网站可以运行查看。


#include <stdio.h>
 
// 联合体用于类型转换
typedef union {
    double num;
    unsigned long long bits;
} DoubleBits;
 
void printBinary(double num) {
    DoubleBits converter;
    converter.num = num;
 
    // 从最高位到最低位逐位输出
    for (int i = (sizeof(converter.bits) * 8) - 1; i >= 0; --i) {
        unsigned long long mask = 1ULL << i;  // 构造掩码
 
        // 使用掩码进行与运算判断该位是0还是1
        int bit = (converter.bits & mask) ? 1 : 0;
 
        printf("%d", bit);
 
        if (i % 8 == 0) {
            printf(" ");  // 每8位添加一个空格
        }
    }
 
    printf("\n");
}
 
int main() {
    double num = 1.111; // input your number
 
    printf("二进制表示为：");
    printBinary(num);
 
    return 0;
}