n-grams语言模型——【torch学习笔记】

语言模型

引用翻译：《动手学深度学习》

文本是序列数据的一个重要例子。事实上，我们将使用自然语言模型作为本章中许多例子的基础。鉴于此，值得对一些事情进行更详细的讨论。在下文中，我们将把单词（或字符序列）视为离散观察的时间序列。假设长度为T的文本中的词依次为w1;w2;…;wT，那么，在离散时间序列中，wt(1 < t < T)可以被视为时间步骤t的输出或标签。

$$p(w_1,w_2,\dots ,w_T).$$

语言模型是非常有用的。例如，一个理想的语言模型能够自行生成自然文本，只需一次画一个词wt ~ p(w_t|w_t-1; . . .w₁ ) 与使用打字机的猴子完全不同，从这样一个模型中出现的所有文本都会被视为自然语言，例如英语文本。此外，它足以生成一个有意义的对话，只需将文本置于先前的对话片段中即可。显然，我们离设计这样一个系统还很远，因为它需要理解文本，而不仅仅是生成符合语法的内容。

然而，语言模型即使在其有限的形式下也是非常有用的。例如， ‘to recognize speech’ and ‘to wreck a nice beach’ 这两个短语听起来非常相似。这可能会在语音识别中引起歧义，而这种歧义通过语言模型很容易解决，因为语言模型会拒绝第二种翻译，认为它很荒唐。同样，在一个文件总结算法中，值得知道的是’狗咬人’比’人咬狗’的频率高得多，或者’让我们吃奶奶’是一个相当令人不安的说法，而’让我们吃，奶奶’则要良性得多。

一、估算一个语言模型

一个显而易见的问题是，我们应该如何对一个文件，甚至是一个词的序列进行建模。我们可以求助于我们在上一节中应用于序列模型的分析。让我们从应用基本的概率规则开始。

$$p(w_1,w_2,\dots ,w_T)=\prod _{t=1}^{T}p(w_t|w_1,\dots ,w_{t-1}).$$

例如，一个包含四个由单词和标点符号组成的文本序列的概率将被给出：

$$p(\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{s},\mathrm{i}\mathrm{s},\mathrm{f}\mathrm{u}\mathrm{n},.)=p(\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{s})p(\mathrm{i}\mathrm{s}|\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{s})p(\mathrm{f}\mathrm{u}\mathrm{n}|\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{s},\mathrm{i}\mathrm{s})p(.|\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{s},\mathrm{i}\mathrm{s},\mathrm{f}\mathrm{u}\mathrm{n}).$$

为了计算语言模型，我们需要计算单词的概率和给定前几个单词的条件概率，即语言模型参数。

在这里，我们假设训练数据集是一个大型文本语料库，如所有维基百科条目、古腾堡计划或网上发布的所有文本。词语的概率可以通过训练数据集中给定词语的相对词频来计算。

例如，p(Statistics)可以被计算为任何以 "统计 "一词开始的句子的概率。一个稍微不那么准确的方法是计算 "统计 "这个词的所有出现次数，然后将其除以语料库中的总词数。

这种方法的效果相当好，特别是对于频繁出现的词。

$$\hat{p}(\mathrm{i}\mathrm{s}|\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{s})=\frac{n(\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{s})}{n(\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{s})}.$$

为了计算语言模型，我们需要计算单词的概率和给定前几个单词的条件概率，即语言模型参数。

在这里，我们假设训练数据集是一个大型文本语料库，如所有维基百科条目、古腾堡计划或网上发布的所有文本。

词语的概率可以通过训练数据集中给定词语的相对词频来计算。例如，p(Statistics)可以被计算为任何以 "Statistics "一词开始的句子的概率。

一个稍微不那么准确的方法是计算 "统计 "这个词的所有出现次数，然后将其除以语料库中的总词数。这种方法的效果相当好，特别是对于频繁出现的词。

一个常见的策略是进行某种形式的拉普拉斯平滑。我们在讨论天真贝叶斯的时候已经遇到过这个问题，当时的解决方案是在所有计数上增加一个小常数。这有助于处理单数，例如，通过

p ^ ( w ) = n ( w ) + ϵ 1 / m n + ϵ 1   p ^ ( w ′ ∣ w ) = n ( w , w ′ ) + ϵ 2 p ^ ( w ′ ) n ( w ) + ϵ 2   p ^ ( w ′ ′ ∣ w ′ , w ) = n ( w , w ′ , w ′ ′ ) + ϵ 3 p ^ ( w ′ , w ′ ′ ) n ( w , w ′ ) + ϵ 3

$$\begin{aligned} \hat{p}(w) & = \frac{n(w) + \epsilon_1/m}{n + \epsilon_1} \ \hat{p}(w'|w) & = \frac{n(w,w') + \epsilon_2 \hat{p}(w')}{n(w) + \epsilon_2} \ \hat{p}(w''|w',w) & = \frac{n(w,w',w'') + \epsilon_3 \hat{p}(w',w'')}{n(w,w') + \epsilon_3} \end{aligned}$$ p^​(w)​=n+ϵ1​n(w)+ϵ1​/m​ p^​(w′∣w)​=n(w)+ϵ2​n(w,w′)+ϵ2​p^​(w′)​ p^​(w′′∣w′,w)​=n(w,w′)+ϵ3​n(w,w′,w′′)+ϵ3​p^​(w′,w′′)​​

这里的系数ϵi>0决定了我们在多大程度上使用较短序列的估计值作为较长序列的填充。此外，m是我们遇到的词的总数。以上是Kneser-Ney平滑法和贝叶斯非参数法可以完成的一个相当原始的变体。

关于如何实现这一目标的更多细节，见Wood等人的Sequence Memoizer, 2012。不幸的是，这样的模型很快就会变得笨重：首先，我们需要存储所有的计数，其次，这完全忽略了词的含义。

例如，"猫 "和 "猫 "应该出现在相关的语境中。基于深度学习的语言模型很适合考虑到这一点。这一点，要根据额外的语境调整这种模型是相当困难的。

最后，长的单词序列几乎可以肯定是新的，因此，简单地计算以前看到的单词序列的频率的模型在那里一定会表现不佳。

二、马尔科夫模型和n-grams

在我们讨论涉及深度学习的解决方案之前，我们还需要一些术语和概念。回顾我们在上一节中对马尔可夫模型的讨论。让我们把它应用于语言建模。如果p(wt+1|wt; . .w1)=p(wt+1|wt)，则序列上的分布满足一阶马尔科夫属性。更高的阶数对应于更长的依赖关系。这就导致了我们可以应用一些近似值来为序列建模。

p ( w 1 , w 2 , w 3 , w 4 ) = p ( w 1 ) p ( w 2 ) p ( w 3 ) p ( w 4 )   p ( w 1 , w 2 , w 3 , w 4 ) = p ( w 1 ) p ( w 2 ∣ w 1 ) p ( w 3 ∣ w 2 ) p ( w 4 ∣ w 3 )   p ( w 1 , w 2 , w 3 , w 4 ) = p ( w 1 ) p ( w 2 ∣ w 1 ) p ( w 3 ∣ w 1 , w 2 ) p ( w 4 ∣ w 2 , w 3 )

$$\begin{aligned} p(w_1, w_2, w_3, w_4) &= p(w_1) p(w_2) p(w_3) p(w_4)\ p(w_1, w_2, w_3, w_4) &= p(w_1) p(w_2 | w_1) p(w_3 | w_2) p(w_4 | w_3)\ p(w_1, w_2, w_3, w_4) &= p(w_1) p(w_2 | w_1) p(w_3 | w_1, w_2) p(w_4 | w_2, w_3) \end{aligned}$$ p(w1​,w2​,w3​,w4​)​=p(w1​)p(w2​)p(w3​)p(w4​) p(w1​,w2​,w3​,w4​)​=p(w1​)p(w2​∣w1​)p(w3​∣w2​)p(w4​∣w3​) p(w1​,w2​,w3​,w4​)​=p(w1​)p(w2​∣w1​)p(w3​∣w1​,w2​)p(w4​∣w2​,w3​)​

由于它们涉及一个、两个或三个术语，这些模型通常被称为单字、大字和三字模型。在下文中，我们将学习如何设计更好的模型。

三、自然语言统计

让我们看看这在真实数据上是如何工作的。为了开始，我们从H.G. Wells的《时间机器》中加载文本。这是一个相当小的语料库，只有3万多字，但对于我们要说明的目的来说，这就足够了。更现实的文件集包含数十亿字。首先，我们将文件拆分为单词，并忽略标点符号和大写字母。虽然这放弃了一些相关的信息，但对于计算一般的计数统计是很有用的。让我们看看前几行是什么样子的。

import sys
sys.path.insert(0, '..')

import collections
import re
1
2
3
4
5

with open('../data/timemachine.txt', 'r') as f:
    lines = f.readlines()
    raw_dataset = [re.sub('[^A-Za-z]+', ' ', st).lower().split() for st in lines]

for st in raw_dataset[8:12]:
    print('tokens:', len(st), st)
1
2
3
4
5
6

tokens: 13 ['the', 'time', 'traveller', 'for', 'so', 'it', 'will', 'be', 'convenient', 'to', 'speak', 'of', 'him']
tokens: 12 ['was', 'expounding', 'a', 'recondite', 'matter', 'to', 'us', 'his', 'grey', 'eyes', 'shone', 'and']
tokens: 11 ['twinkled', 'and', 'his', 'usually', 'pale', 'face', 'was', 'flushed', 'and', 'animated', 'the']
tokens: 10 ['fire', 'burned', 'brightly', 'and', 'the', 'soft', 'radiance', 'of', 'the', 'incandescent']
1
2
3
4

现在我们需要将其插入到一个单词计数器中。这就是集合数据结构派上用场的地方。它为我们处理了所有的会计工作。

counter = collections.Counter([t for s in raw_dataset for t in s])
print(" 'traveller'的词频:", counter['traveller'])

print(counter.most_common(10))
1
2
3
4

frequency of 'traveller': 61
[('the', 2261), ('i', 1267), ('and', 1245), ('of', 1155), ('a', 816), ('to', 695), ('was', 552), ('in', 541), ('that', 443), ('my', 440)]
1
2

正如我们所看到的，最流行的词其实是很无聊的，看都看不过来。在传统的NLP中，它们通常被称为停止词，因此被过滤掉了。

也就是说，它们仍然带有意义，尽管如此，我们还是会使用它们。然而，有一件事是相当清楚的，那就是词的频率衰减得相当快。第10个词的频率还不到最受欢迎的那个词的1/5。为了得到一个更好的概念，我们绘制了单词频率的图表。

%matplotlib inline
from matplotlib import pyplot as plt
1
2

wordcounts = [count for i,count in counter.most_common()]
plt.loglog(wordcounts);
1
2

​

​

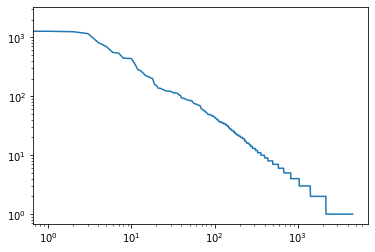
我们在这里发现了一些很基本的东西–词的频率以一种明确的方式迅速衰减。在处理了前四个词的例外情况（“the”、“i”、“and”、“of”）之后，所有剩下的词在对数图上都遵循一条直线。这意味着单词符合Zipf定律，该定律指出，项目频率由以下公式给出

n(x) ~ (x + c) -a，因此log n(x) = -a log(x + c) + const。

如果我们想通过计数统计和平滑化来建立单词模型，这应该已经让我们暂停了。毕竟，我们将大大高估尾部的频率，也就是不经常出现的词。但是词对（以及三词租和更多的）呢？让我们来看看。

for st in raw_dataset[0:1]:
    print(st)
    for tk in st:
        print(tk)
1
2
3
4

['the', 'time', 'machine', 'by', 'h', 'g', 'wells']
the
time
machine
by
h
g
wells
1
2
3
4
5
6
7
8

wse = wseq[0:11]  # 取样例
print(wse)
word_pairs = [pair for pair in zip(wse[:-1], wse[1:])]
print(word_pairs)  # 计算相邻词语的组合，存储为元组
1
2
3
4

['the', 'time', 'machine', 'by', 'h', 'g', 'wells', 'i', 'the', 'time', 'traveller']
[('the', 'time'), ('time', 'machine'), ('machine', 'by'), ('by', 'h'), ('h', 'g'), ('g', 'wells'), ('wells', 'i'), ('i', 'the'), ('the', 'time'), ('time', 'traveller')]
1
2

# raw_dataset是按行分词的子列表
wseq = [tk for st in raw_dataset for tk in st]  # 即将子列表的元素都展开，将所有词语放于一个列表之中
word_pairs = [pair for pair in zip(wseq[:-1], wseq[1:])]  # 构建词语组合
print('相邻词语组合元组\n', word_pairs[:10])

counter_pairs = collections.Counter(word_pairs)
print('最多的组合形式\n', counter_pairs.most_common(10))
1
2
3
4
5
6
7

相邻词语组合元组
 [('the', 'time'), ('time', 'machine'), ('machine', 'by'), ('by', 'h'), ('h', 'g'), ('g', 'wells'), ('wells', 'i'), ('i', 'the'), ('the', 'time'), ('time', 'traveller')]
最多的组合形式
 [(('of', 'the'), 309), (('in', 'the'), 169), (('i', 'had'), 130), (('i', 'was'), 112), (('and', 'the'), 109), (('the', 'time'), 102), (('it', 'was'), 99), (('to', 'the'), 85), (('as', 'i'), 78), (('of', 'a'), 73)]
1
2
3
4

有两件事是值得注意的。在10个最频繁的词对中，有9个是由停止词组成的，只有一个与实际的书有关–“时间”。让我们看看大词频率的表现是否与单词频率的表现相同。

word_triples = [triple for triple in zip(wseq[:-2], wseq[1:-1], wseq[2:])]  # 相邻的三个词语组合
counter_triples = collections.Counter(word_triples)  # 对相邻的三个词语组合进行计数

print('相邻的三个词语组合进行计数\n', counter_triples.most_common(10))
1
2
3
4

相邻的三个词语组合进行计数
 [(('the', 'time', 'traveller'), 59), (('the', 'time', 'machine'), 30), (('the', 'medical', 'man'), 24), (('it', 'seemed', 'to'), 16), (('it', 'was', 'a'), 15), (('here', 'and', 'there'), 15), (('seemed', 'to', 'me'), 14), (('i', 'did', 'not'), 14), (('i', 'saw', 'the'), 13), (('i', 'began', 'to'), 13)]
1
2

word_triples = [triple for triple in zip(wseq[:-2], wseq[1:-1], wseq[2:], wseq[3:])]  # 相邻的4个词语组合
four_triples = collections.Counter(word_triples)  # 对相邻的4个词语组合进行计数
print('相邻的四个词语组合进行计数\n', four_triples)
1
2
3

# wordcounts是单个词语的计数
wordcounts = [count for i,count in counter.most_common()]
bigramcounts = [count for _,count in counter_pairs.most_common()]  # 两个词语组合计数，只显示top数量
triplecounts = [count for _,count in counter_triples.most_common()]  # 三个词语组合计数，只显示top数量
fourcounts = [count for _,count in four_triples.most_common()]  # 4个词语组合计数，只显示top数量

plt.loglog(wordcounts, label='word counts'); 
plt.loglog(bigramcounts, label='bigram counts');
plt.loglog(triplecounts, label='triple counts');
plt.loglog(fourcounts, label='four counts');
plt.legend();
1
2
3
4
5
6
7
8
9
10
11

​

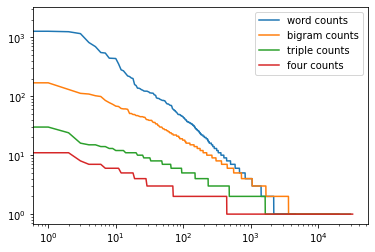
这张图是相当令人兴奋的，原因有很多。首先，除了单词之外，单词序列似乎也在遵循Zipf定律，尽管指数较低，但取决于序列长度。其次，独特的n-grams的数量并不多。这给了我们希望，语言中存在相当多的结构。第三，许多n-grams出现得非常少，这使得拉普拉斯平滑法相当不适合用于语言建模。因此，我们将使用基于深度学习的模型。

四、摘要

• 语言模型是自然语言处理的一项重要技术。

• n-grams通过截断依赖关系为处理长序列提供了一个方便的模型。

• 长序列有一个问题，即它们很少或从未出现。这就需要进行平滑处理，例如通过贝叶斯非参数化或通过深度学习。

• Zipf法则支配着unigrams和n-grams的单词分布。

• 有很多结构，但没有足够的频率来通过平滑处理不频繁的单词组合。