动态规划之最优的子结构属性（Optimal Substructure Property）_最优子结构性质

原文地址：http://www.geeksforgeeks.org/dynamic-programming-set-2-optimal-substructure-property/

As we discussed in Set 1, following are the two main properties of a problem that suggest that the given problem can be solved using Dynamic programming.

1) Overlapping Subproblems
2) Optimal Substructure

正如我们在第一部分讨论的，如果问题具有下面两个属性，那么这个问题就预示着可以用动态规划的方法解决。

We have already discussed Overlapping Subproblem property in the Set 1. Let us discuss Optimal Substructure property here.

我们已经在第一部分讨论了重叠的子问题属性，下来讨论一下最优的子结构属性。

2) Optimal Substructure: A given problems has Optimal Substructure Property if optimal solution of the given problem can be obtained by using optimal solutions of its subproblems.

2）最优的子结构：如果一个问题最优的解决方案可以通过最优它的子问题的解决方案来获取，那么这个问题就用最优子结构的属性。
For example the shortest path problem has following optimal substructure property: If a node x lies in the shortest path from a source node u to destination node v then the shortest path from u to v is combination of shortest path from u to x and shortest path from x to v. The standard All Pair Shortest Path algorithms like Floyd–Warshall and Bellman–Ford are typical examples of Dynamic Programming.

例如最短路径问题就有最优子结构属性：如果一个节点x在开始节点u，终点为v的最短路径上的时候，那么从u到v的最短路径就是从u到x的最短路径加上从x到v的最短路径。像Floyd–Warshall和Bellman–Ford的标准所以最短路径算法是典型的动态规划的例子。

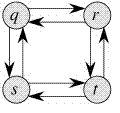
On the other hand the Longest path problem doesn’t have the Optimal Substructure property. Here by Longest Path we mean longest simple path (path without cycle) between two nodes. Consider the following unweighted graph given in the CLRS book. There are two longest paths from q to t: q -> r ->t and q ->s->t. Unlike shortest paths, these longest paths do not have the optimal substructure property. For example, the longest path q->r->t is not a combination of longest path from q to r and longest path from r to t, because the longest path from q to r is q->s->t->r.

另外最长路径问题不具有最优子结构的属性，我们这里所说的最长路径是两个节点之间的最长简单路径（路径没有环），CLRS（译者注：这个书咱也不知道啥玩意儿，忽略即可，不影响理解文章）给出了下面的无权图。从q到t有两条最长的路径：q -> r ->t与q ->s->t。与最短路径不同，这些最长路径没有最优的子结构属性。例如，最长路径q -> r ->t不能q 到r的最长路径与r到t的最长路径的结合，因为从q到r的最长路径是 q ->s->t->r。

We will be covering some example problems in future posts on Dynamic Programming.

我们将在后面的动态规划的文章中涉及到一些例子。