归并排序算法(经典、常见)

今天我们不刷力扣了，我们来复习（手撕）一下数据结构中的八大排序算法之一，---排序

基本概念：

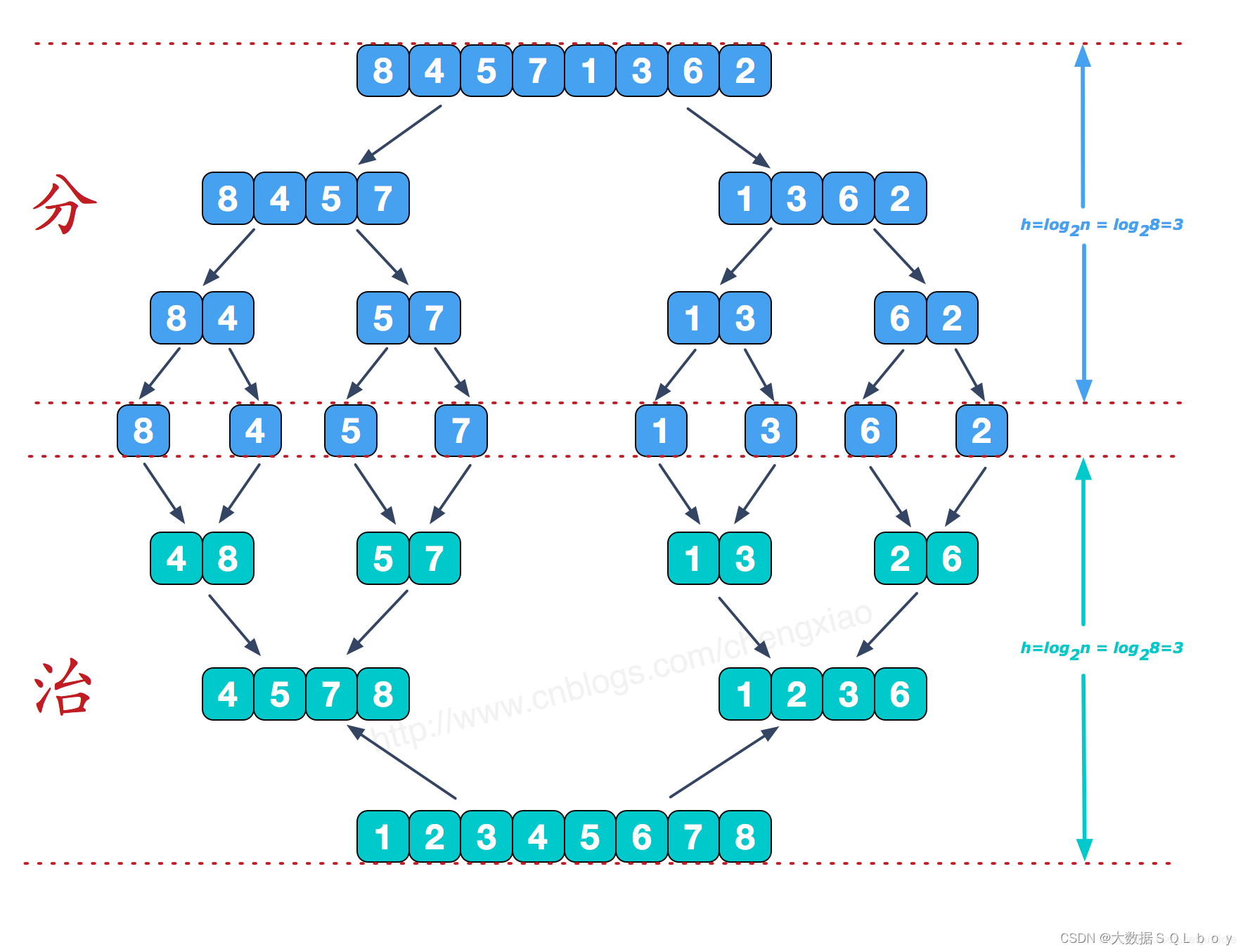
归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

分治法：

   基本思想：
将一个规模为n的问题分解为k个规模较小的子问题，这些子问题互相独立且原问题相同。递归地解这些子问题，然后将各子问题的解合并得到原问题的解。
   精髓：
       分——将问题分解为规模更小的子问题。
       治——将这些规模更小的子问题逐个击破。
       合——将已解决的子问题合并，最终得到原问题的解。

动图演示： 

代码实现：

import java.util.Arrays;
 
//归并排序：先分再合
public class MergeSort {
    public static void main(String[] args) {
        int[] arr = {3,1,4,6,22,0,33,2,745,5,56,8};
        int[] temp = new int[arr.length];
        System.out.println("未排序数组："+ Arrays.toString(arr));
        mergeSort(arr,0,arr.length-1,temp);
        System.out.println("已排序数组："+ Arrays.toString(arr));
    }
 
    //mergeSort（）方法：将数组分组出来
    public static void mergeSort(int[] arr,int left,
                                    int right,int[] temp){
        //将数组进行分组
        if (left < right){
            int l = left;
            int r = right;
            int middle = (l+r)/2;
 
            //将分组进行排序整合
            merge(arr,left,middle,right,temp);//将左边的部分继续分
            mergeSort(arr,0,middle,temp);//将右边的部分继续分
            mergeSort(arr,middle+1,r,temp);
        }
    }
 
    public static void merge(int[] arr,int left,int middle,int right,int[] temp){
        int l = left;
        int r = middle+1;
        int t = 0;
       
         //用于临时数组下标索引
        while(l <= middle && r <= right){
        //先将两个部分整合
            temp[t++] = arr[l] <= arr[r]?arr[l++] : arr[r++];
        }
        //如果左边的部分还有元素没有被合并，则接着l继续合并
        while(l <= middle){
            temp[t++] = arr[l++];
        }
        //如果右边的部分还有元素没有被合并，则接着r继续合并
        while (r <= right){
            temp[t++] = arr[r++];
        }
        //将temp临时数组中的元素顺序传到arr数组中
        t = 0;
        int tempLeft = left;
        while(tempLeft <= right){
            arr[tempLeft] = temp[t];
            tempLeft++;
            t++;
        }
    }
}

代码分析：

基本思路：

步骤：1.将序列中待排序数字分为若干组，每个数字分为一组

           2.将若干个组两两合并，保证合并后的组是有序的

           3.重复第二步操作直到只剩下一组，排序完成

基本思路：

       归并排序，先将数组进行拆分，每次拆成两份，然后继续拆分直到一组有两个元素为止，然后再进行两两整合排序，重复两两整合排序直至数组元素排序完成。

平均时间复杂度：O（nlogn）

注意：

 temp[t++] = arr[l] <= arr[r]?arr[l++] : arr[r++];
即  
       if (arr[l] <= arr[r]){
                temp[t] = arr[l];
               t++;l++;
           }else{
               temp[t] = arr[r];
               t++;r++;
            }
 
 
  temp[t++] = arr[l++];
即
           temp[t] = arr[l];
           t++;l++;
 
 
 
 temp[t++] = arr[r++];
即
 
            temp[t] = arr[r];
            t++;r++;