小小林熬夜学编程

这个屌丝很懒，什么也没留下！

热门标签

阈值向量误差修正模型TVECM对汇率金融时间序列数据分析|附数据代码

作者：小小林熬夜学编程 | 2024-06-13 15:29:33

踩

全文链接：https://tecdat.cn/?p=36380

在全球金融市场中，汇率作为连接不同国家货币价值的桥梁，其动态变化对全球经济活动、贸易和投资具有深远影响。随着金融市场的日益复杂化和全球化，汇率时间序列数据展现出高度的非线性、非对称性和动态性特征，使得传统的线性模型在分析时面临挑战。因此，探索适用于分析汇率金融时间序列数据的非线性模型，对于深入理解汇率波动机制、指导金融投资决策具有重要意义（点击文末“阅读原文”获取完整代码数据）。

阈值向量误差修正模型（Threshold Vector Error Correction Model, TVECM）作为一种非线性计量经济学模型，近年来在汇率数据分析领域受到了广泛关注。该模型通过引入阈值机制，能够捕捉汇率时间序列数据在不同状态下的非线性动态特征，从而更准确地刻画汇率波动的复杂性和多样性。与传统的向量误差修正模型（VECM）相比，TVECM模型不仅能够分析变量之间的长期均衡关系，还能进一步探讨变量在短期内对均衡偏离的调整过程，特别是在不同阈值状态下的调整差异。

本文旨在应用R语言TVECM模型帮助客户对汇率金融时间序列数据进行深入分析。首先，我们将对TVECM模型的理论基础、模型设定和估计方法进行系统介绍，为读者提供全面的模型背景知识。其次，我们将选择具有代表性的汇率数据作为研究样本，运用TVECM模型进行实证分析，探讨汇率在不同阈值状态下的动态特征和调整机制。最后，我们将对实证结果进行解释和讨论，为汇率预测、风险管理和政策制定提供有价值的参考。

读取数据

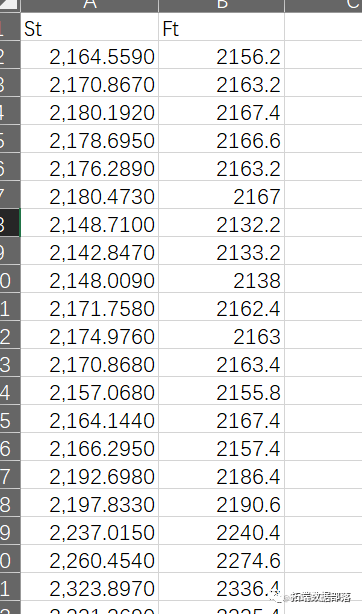
首先，我们从CSV文件中读取所需的数据集。这个数据集包含了与汇率和其他金融指标相关的历史数据。我们使用read.csv函数读取名为"data.csv"的文件，并使用na.omit函数去除任何包含缺失值（NA）的观测值。最后，我们利用head函数预览数据集的前几行，以确保数据已被正确加载和清洗。

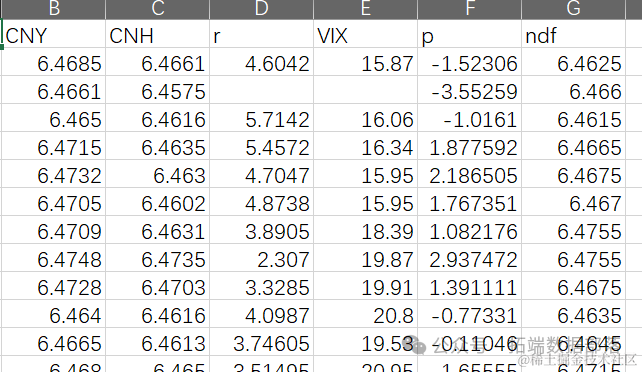
在R环境中，我们执行以下代码准备数据集：


# 读取数据  
 
	data <- read.csv("data.csv")  
 
	  
 
	# 去除缺失值  
 
	data <- na.omit(data)  
 
	  
 
	# 预览数据集的前几行  
 
	head(data)

执行上述代码后，我们得到以下数据集的前几行输出：

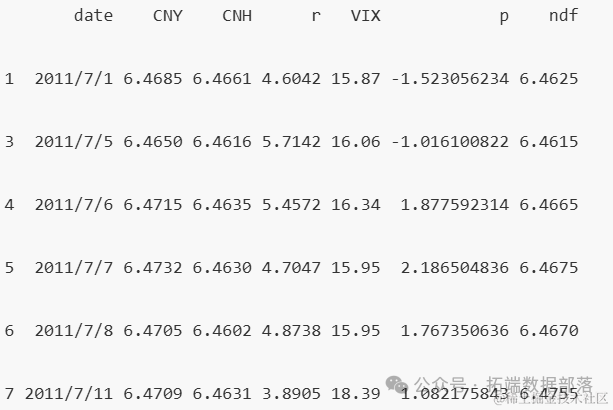
从上述输出中，我们可以看到数据集包含了日期（date）、人民币在岸汇率（CNY）、人民币离岸汇率（CNH）、利率（r）、波动性指数（VIX）、某种收益率（p）和远期汇率（ndf）等变量。这些变量将为后续的数据动态分析提供基础。

阈值向量误差修正模型

在本文中，我们将对金融时间序列数据进行深入分析，特别是关注于零利率数据（zeroyld）。为了捕捉数据中的非线性动态和潜在的结构性变化，我们将使用阈值向量误差修正模型（Threshold Vector Error Correction Model, TVECM）对数据进行分析。TVECM模型能够有效地处理具有不同动态特性的数据子集，从而提供更准确的预测和解释。

方法

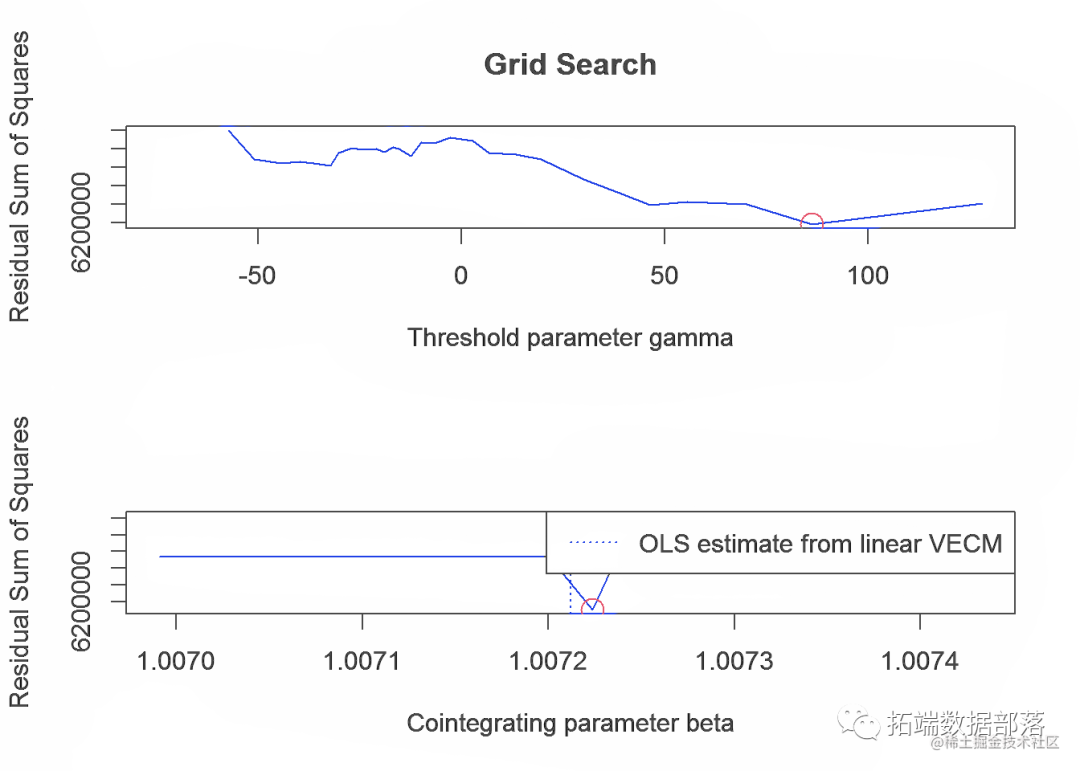
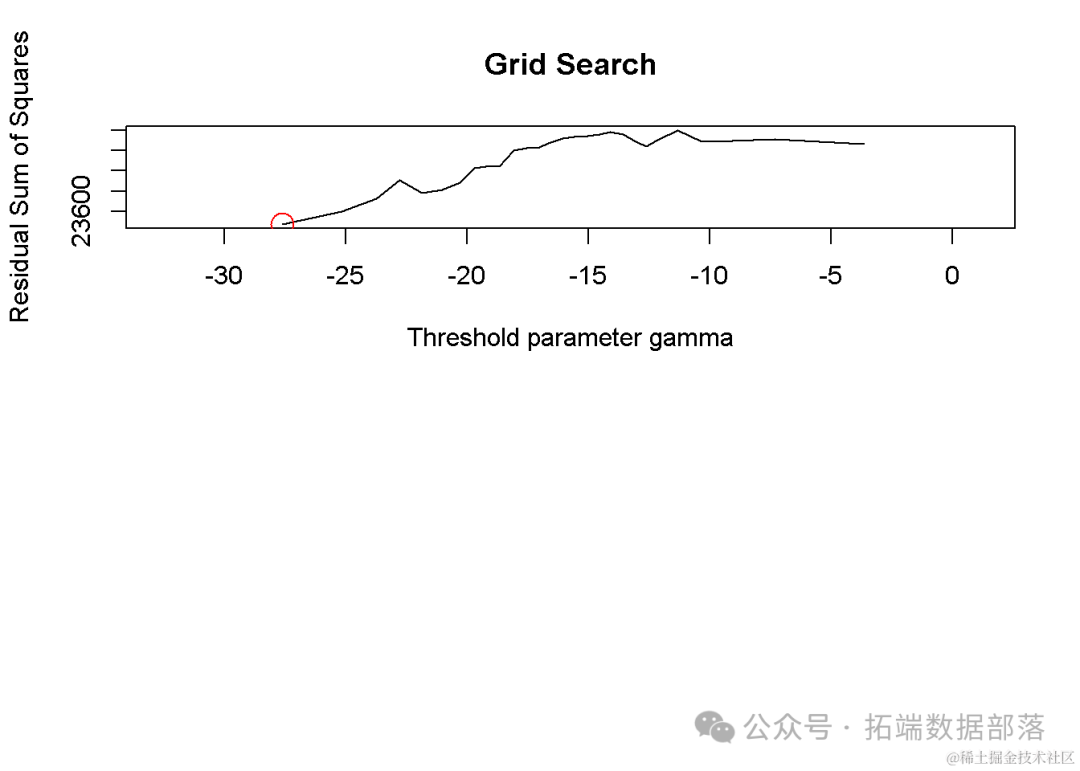
我们使用R语言来估计TVECM模型。在设定模型参数时，我们选择了两个阈值（nthresh=2）、一阶滞后（lag=1）、以及β和θ的网格大小分别为60和30。此外，我们还设置了plot=TRUE以便在估计过程中生成图形，并使用trim=0.05来排除观测值百分比低于5%的网格点。我们还为β的截距项设定了一个范围，以限制其取值范围。

在执行TVECM模型估计后，我们观察到网格中有大量点（占93.4%）的观测值百分比低于我们设定的修剪阈值（trim），因此这些点没有被计算。这表明我们的网格设置相对较为宽松，但这也为我们提供了一个广泛的搜索空间以寻找最佳模型参数。

在模型估计过程中，我们得到了多个重要的统计量。首先，最佳阈值从第一次搜索中得出为-0.0464，这表明当某个指标超过这个阈值时，数据的动态特性可能会发生变化。其次，我们得到了最佳协整值（cointegrating value）为0.9915254，这为我们提供了关于变量之间长期均衡关系的信息。

此外，我们还注意到在条件步骤和迭代步骤中，存在多个阈值值使得残差平方和（SSR）最小化。在这种情况下，我们选择了第一个找到的阈值作为最佳阈值。同时，我们还记录了第二好的阈值组合以及对应的SSR值，以便后续分析和比较。

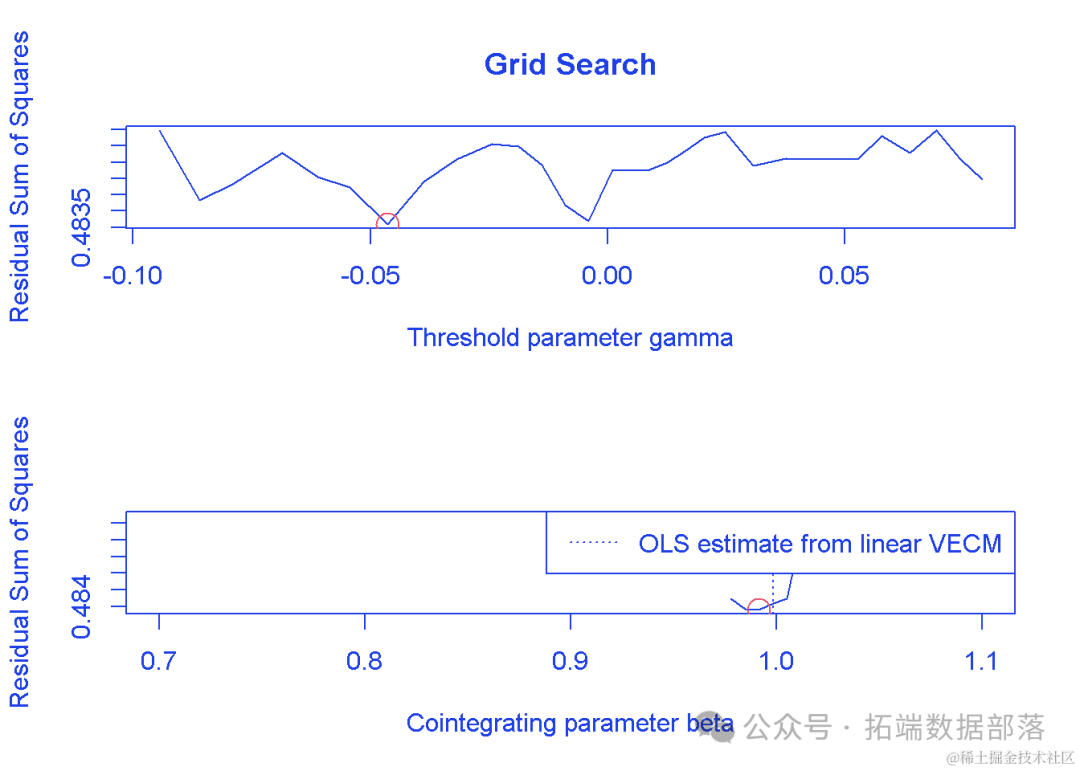
阈值向量误差修正模型（TVECM）的参数估计结果

在本文中，我们采用了阈值向量误差修正模型（TVECM）来分析两组时间序列数据——CNY和CNH。该模型通过引入阈值来捕捉数据中的非线性动态特性，并允许在数据状态变化时模型的参数发生变化。以下是基于我们分析的数据集所得到的TVECM模型参数估计结果。

最佳阈值与协整值
在首次搜索中，我们找到了最佳的阈值组合为-0.0464。此外，模型估计出的最佳协整值为0.9915254，这为我们提供了关于CNY和CNH之间长期均衡关系的量化信息。

条件步骤与迭代步骤中的阈值选择
在条件步骤中，存在两个阈值值能够使模型的残差平方和（SSR）最小化，其中第一个被选取作为最佳阈值。具体而言，这两个阈值分别是-0.0464和-0.0077，对应的SSR值为0.4777522。在迭代步骤中，有12个阈值值能够最小化SSR，其中第一个同样被选为最佳阈值。进一步地，我们发现在迭代步骤的第二个最佳阈值组合为-0.0465和-0.0077，其对应的SSR值同样为0.4777522。

模型参数估计
基于上述选定的阈值，我们进一步估计了TVECM模型的具体参数。模型被划分为三个区域，分别对应不同的数据状态：低阈值区（Bdown）、中阈值区（Bmiddle）和高阈值区（Bup）。每个区域下的模型参数如下所示：

在低阈值区（Bdown）：

CNY方程的ECT系数为0.04127052，常数项为0.0035734604，CNY滞后一期的系数为0.5282863，CNH滞后一期的系数为0.1445567。
CNH方程的ECT系数为0.10803644，常数项为0.0005762515，CNY滞后一期的系数为0.5141541，CNH滞后一期的系数为-0.1892094。

在中阈值区（Bmiddle）：

CNY方程的ECT系数为-0.1582852，常数项为-0.002609754，CNY滞后一期的系数为0.09435307，CNH滞后一期的系数为-0.02820711。
CNH方程的ECT系数为-0.1055547，常数项为-0.001718553，CNY滞后一期的系数为0.26851256，CNH滞后一期的系数为0.08174842。

在高阈值区（Bup）：

CNY方程的ECT系数为-0.050136793，常数项为0.003023718，CNY滞后一期的系数为-0.167168087，CNH滞后一期的系数为0.29016151。
CNH方程的ECT系数为-0.008701065，常数项为0.001000574，CNY滞后一期的系数为0.004480175，CNH滞后一期的系数为-0.06013336。

最终，我们选择的阈值组合为-0.0465和-0.0077，这为我们提供了在不同数据状态下，CNY和CNH之间关系的准确描述。

summary(tv)

点击标题查阅往期内容

R语言门限误差修正模型(TVECM)参数估计沪深300指数和股指期货指数可视化

左右滑动查看更多

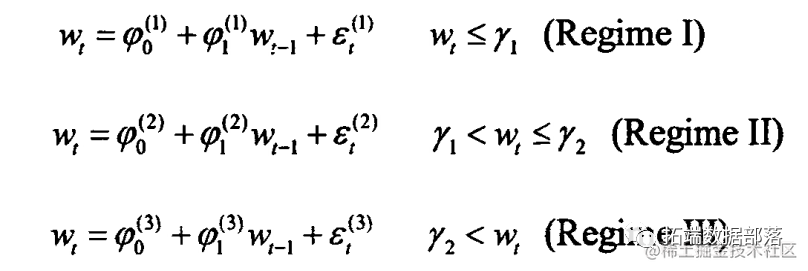
模型选择准则的评估

为了评估我们估计的阈值向量误差修正模型（TVECM）的拟合优度，我们采用了两个常用的模型选择准则：赤池信息准则（Akaike Information Criterion, AIC）和贝叶斯信息准则（Bayesian Information Criterion, BIC）。这两个准则在统计学和计量经济学中广泛应用，旨在帮助研究者选择最符合数据特征的模型。

首先，我们计算了TVECM模型的AIC值，得到的结果为-24727.9。AIC值越小，表示模型对数据的拟合度越高，同时模型的复杂度也相对较低。在这个案例中，AIC值显著为负，表明我们的TVECM模型对数据有很好的拟合效果。


AIC(tv)
BIC(tv)

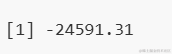
接下来，我们也计算了TVECM模型的BIC值，得到的结果为-24591.31。与AIC类似，BIC值也用于模型选择，但它在考虑模型复杂度时，对模型参数的个数给予了更大的权重。因此，BIC值在模型复杂度较高时增长得更快。尽管如此，我们的TVECM模型仍然得到了一个相对较小的BIC值，这进一步支持了模型对数据的良好拟合。

综上所述，通过AIC和BIC两个模型选择准则的评估，我们可以确信我们所估计的TVECM模型在捕获数据中的动态特性和结构性变化方面表现优异。这为我们后续的数据分析和预测工作提供了坚实的基础。

阈值向量误差修正模型（TVECM）的估计与评估

在本研究中，我们采用了阈值向量误差修正模型（TVECM）来分析一组经济数据，特别是聚焦于CNY和CNH这两个关键变量之间的关系。为了获得模型的最佳参数估计，我们设定了模型的多个参数，包括两个阈值（nthresh=2）、一个滞后阶数（lag=1）、网格搜索中的β参数范围（ngridBeta=60）和阈值范围（ngridTh=30）。此外，我们设置了数据修剪比例为5%（trim=0.05），并使用了一个预定义的β参数列表（beta=list(int=c(0.7, 1.1,1))）来约束模型的参数空间。

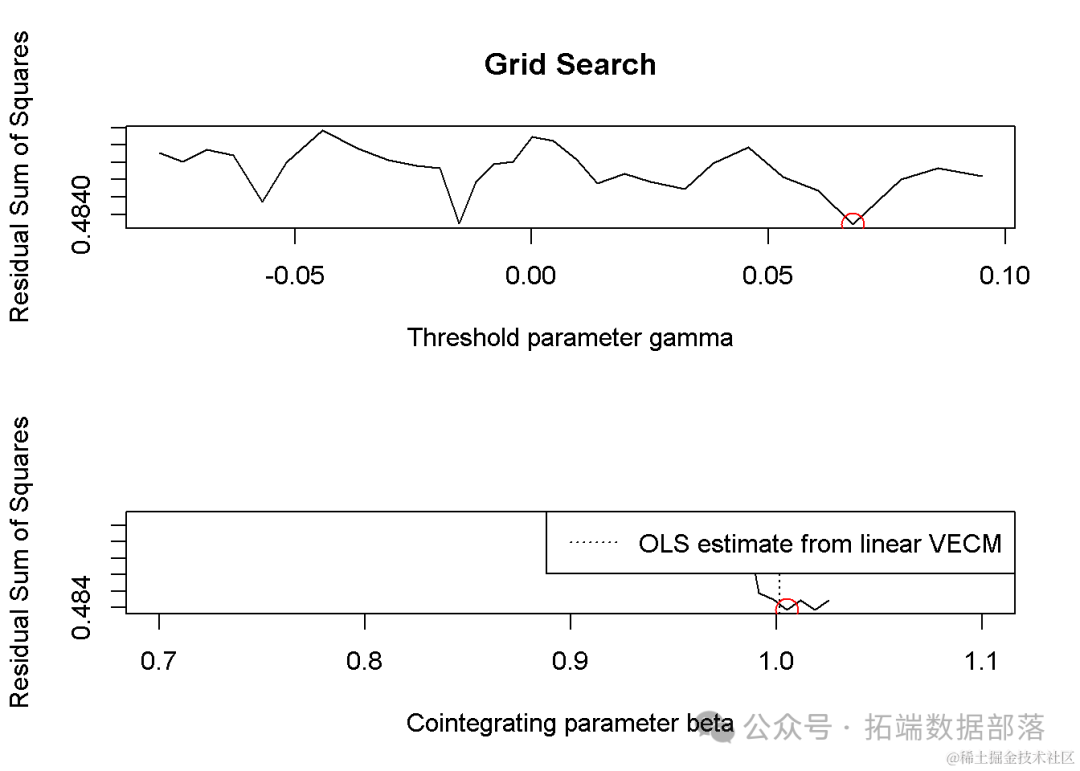
在模型估计过程中，我们注意到有1680个（占93.3%）的网格点所对应的观测值比例低于修剪比例，因此这些点未被计算。这反映了模型估计过程中的数据稀疏性和参数空间的有效约束。

通过模型估计，我们得到了最佳的阈值组合为0.0678。此外，模型估计出的最佳协整值为1.005085，这为我们提供了关于CNY和CNH之间长期均衡关系的量化信息。在条件搜索中，除了最佳阈值外，还找到了一个次优的阈值组合（0.0678和0.0157），对应的残差平方和（SSR）为0.4778545。在迭代步骤中，共有4个阈值组合能够最小化SSR，但首个被选取作为最终模型参数。

为了更详细地了解模型的参数估计结果，我们打印了模型的输出。该模型包含了两个阈值，分别对应低阈值区（Bdown）、中阈值区（Bmiddle）和高阈值区（Bup）。在每个区域内，模型估计出了CNH和CNY的误差修正项（ECT）、常数项（Const）以及它们各自滞后一期的系数。这些参数为我们提供了在不同经济状态下，CNY和CNH之间关系的具体描述。

具体而言，在低阈值区，CNH的ECT系数为0.005964933，CNY的ECT系数为0.053569313。随着阈值的增加，进入中阈值区时，ECT系数有所变化，但保持为正。在高阈值区，CNH的ECT系数变为负值（-0.16603508），而CNY的ECT系数则保持为正但较小（-0.04075862）。这些变化反映了在不同经济状态下，CNY和CNH之间的动态关系。

模型选择准则在阈值向量误差修正模型（TVECM）中的应用

在评估我们估计的阈值向量误差修正模型（TVECM）的拟合优度时，我们采用了两个广泛使用的模型选择准则：赤池信息准则（Akaike Information Criterion, AIC）和贝叶斯信息准则（Bayesian Information Criterion, BIC）。这两个准则在统计学和计量经济学中扮演着至关重要的角色，因为它们能够帮助研究者选择最符合数据特征的模型。


AIC(tvecm)
BIC(tvecm)

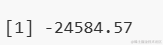
首先，我们计算了TVECM模型的AIC值，得到的结果为-24721.16。AIC值越小，表示模型对数据的拟合度越高，同时模型的复杂度也相对较低。在这个案例中，AIC值显著为负，表明我们的TVECM模型对数据具有优异的拟合效果。

接着，我们也计算了TVECM模型的BIC值，结果为-24584.57。与AIC类似，BIC值也用于模型选择，但它在考虑模型复杂度时，对模型参数的个数给予了更大的权重。因此，BIC值在模型复杂度较高时增长得更快。尽管如此，我们的TVECM模型仍然得到了一个相对较小的BIC值，这进一步支持了模型对数据的良好拟合。

通过综合比较AIC和BIC两个模型选择准则的结果，我们可以确信我们所估计的TVECM模型在捕捉数据中的动态特性和结构性变化方面表现优异。这一结果为后续的经济分析和预测提供了坚实的基础，并增强了我们对模型性能的信心。

然后，使用函数拟合一个阈值向量错误修正模型，模型的输入变量是CNY、CNH和r，阈值的数量为2，滞后期为1，搜索阈值的网格数为60，搜索beta值的网格数为30，trim参数为0.05。模型的输出结果包括best threshold值、best cointegrating value、second best threshold值和second best cointegrating value等信息。

使用summary函数显示模型的汇总信息，包括模型的类型、样本大小、变量数量、参数数量、AIC和BIC值、残差平方和（SSR）等信息。同时，也显示了模型的系数矩阵和阈值信息。

summary(tvecm)

重复上述过程，但是这次输入变量包括CNY、CNH、r和VIX四个变量，阈值的数量仍然为2，其他参数保持不变。

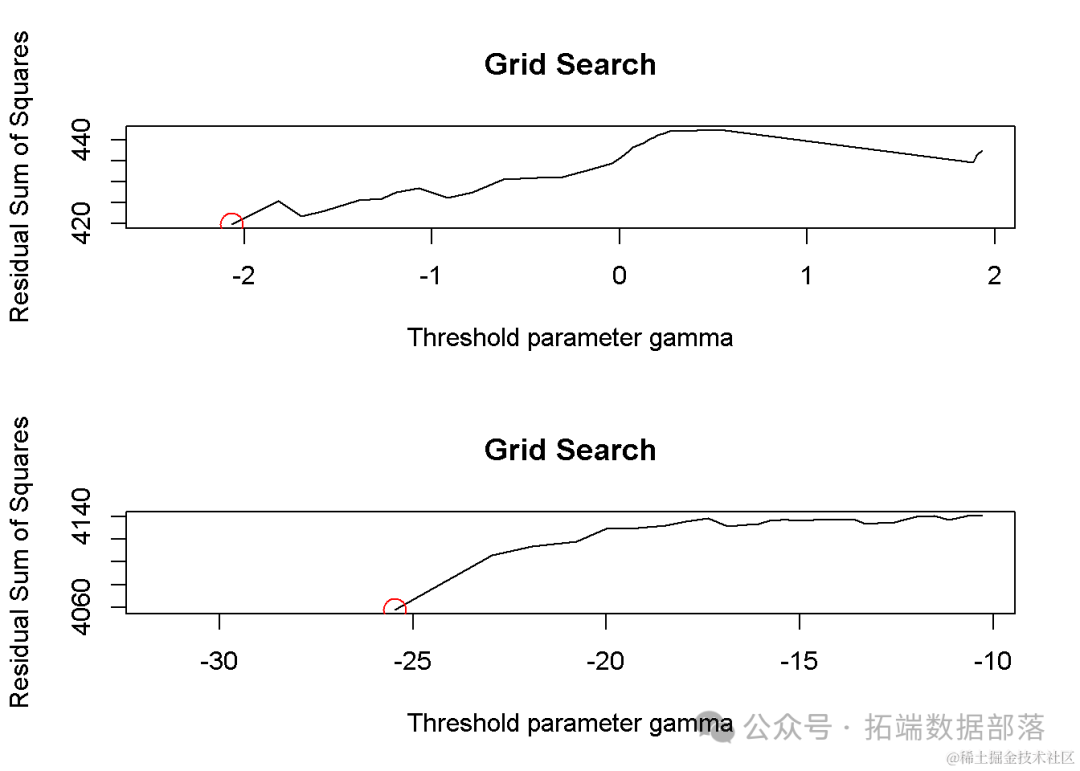
print(tvecm)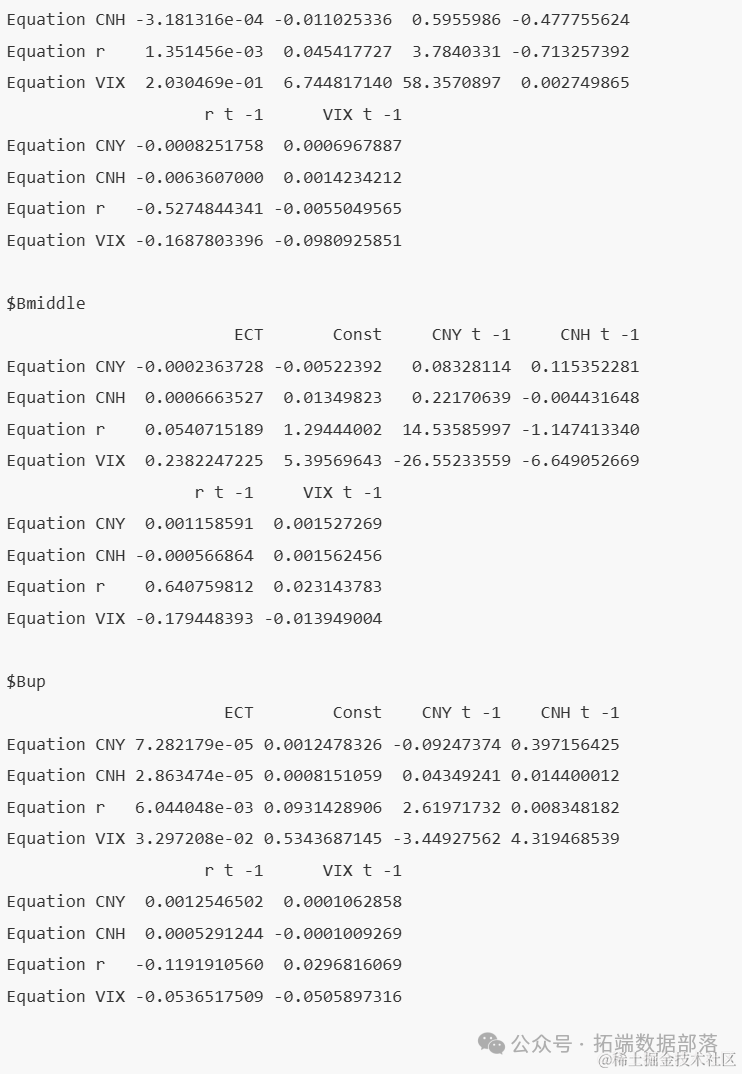

为了确保后续模型估计的准确性，我们决定移除数据集中所有包含缺失值的观测。通过调用na.omit(data)函数，我们成功地去除了含有NA的观测，得到了一个完整的数据集。

随后，我们使用预处理后的数据集进行TVECM模型的估计。通过指定多个参数，如两个阈值（nthresh=2）、一个滞后阶数（lag=1）、β参数的网格搜索范围（ngridBeta=60）和阈值的网格搜索范围（ngridTh=30），我们设置了模型的估计框架。此外，我们还设置了plot=TRUE以在估计过程中生成图形输出，并设定了数据修剪比例为5%（trim=0.05）。特别地，我们为β参数指定了精确的取值范围（exact=c(0.7,1, 1.1,1)）和区间取值范围（int=c(0.7,1, 1,1.1,1,1)），以约束模型的参数空间。

在模型估计过程中，我们注意到有2个（占6.7%）的网格点所对应的观测值比例低于修剪比例，因此这些点未被计算。这表明在参数空间的某些区域，数据的稀疏性导致了模型估计的不稳定性。

通过模型估计，我们得到了最佳的阈值组合，其中第一个搜索步骤得到的最佳阈值为-27.60863。此外，模型还估计出了最佳协整值组合（0.7, 1, 1.1, 1），这为我们提供了关于数据集中各变量之间长期均衡关系的量化信息。在条件搜索中，除了最佳阈值外，还找到了一个次优的阈值组合（-27.60863和1.072377），对应的残差平方和（SSR）为22453.83。在迭代步骤的第二阶段，最佳阈值组合更新为（-27.47267和1.072377），对应的SSR进一步降低至22440.49。

阈值向量误差修正模型（TVECM）的参数估计结果

在进行阈值向量误差修正模型（TVECM）的估计后，我们得到了模型的详细参数估计结果。该模型采用两个阈值（thresholds），旨在捕捉数据中可能存在的非线性结构变化。以下是模型在不同阈值状态下的参数估计值。

print(tvecm)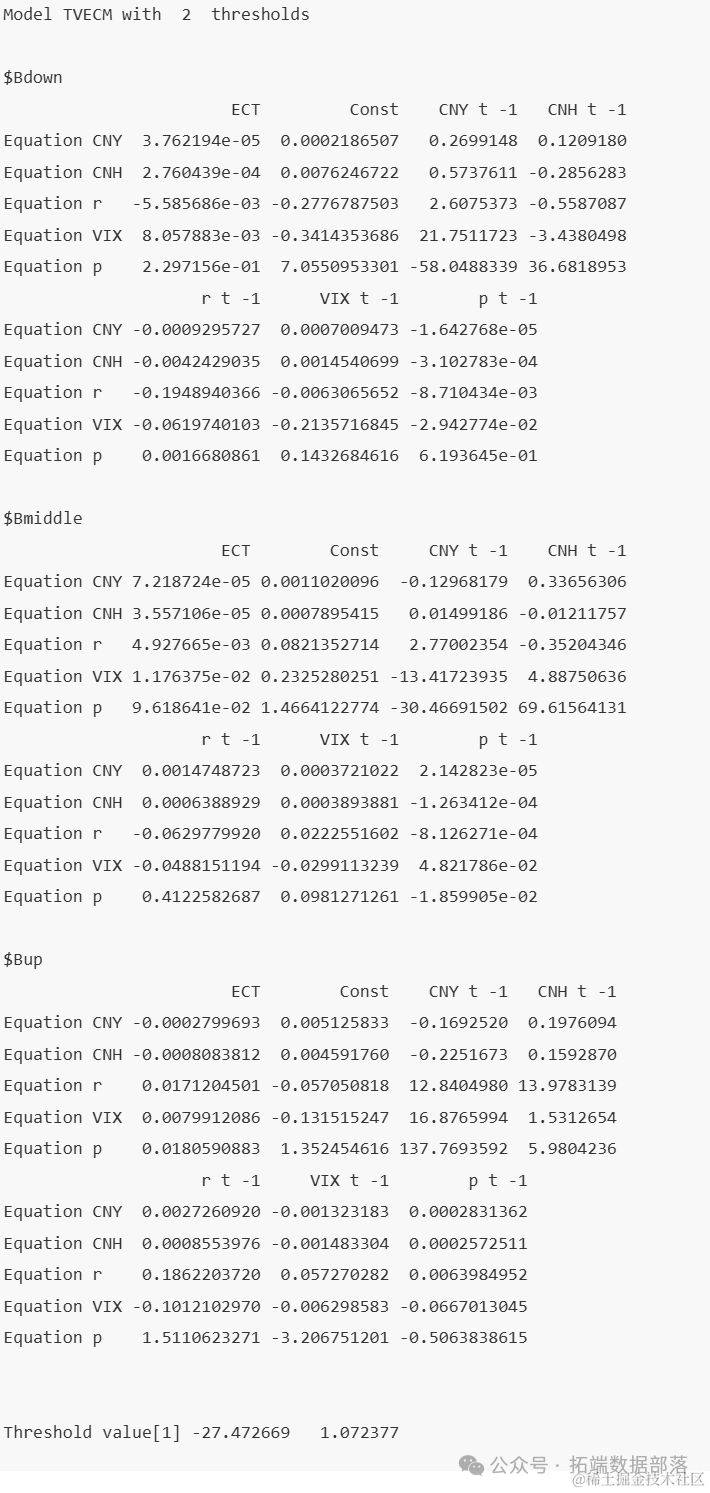

一、低阈值（Bdown）状态下的参数估计

在低阈值状态下，模型的参数估计结果显示了各解释变量对响应变量的影响。具体而言，对于CNY方程，ECT（误差修正项）的系数为3.762194e-05，表明长期均衡关系的偏离对CNY的短期调整具有微小但显著的影响。类似地，Const（常数项）、CNY t -1（CNY的滞后一期值）、CNH t -1（CNH的滞后一期值）等解释变量也呈现出不同的影响方向和程度。其他方程（如CNH、r、VIX、p）也遵循相同的解释逻辑。

二、中阈值（Bmiddle）状态下的参数估计

在中阈值状态下，模型的参数估计结果呈现出与低阈值状态不同的特征。例如，在CNY方程中，ECT的系数增大至7.218724e-05，表明随着系统状态的改变，长期均衡关系的偏离对CNY的短期调整影响有所增强。同样，其他解释变量也表现出与中阈值状态相适应的影响方向和程度。

三、高阈值（Bup）状态下的参数估计

在高阈值状态下，模型的参数估计结果进一步揭示了系统在不同状态下的动态特性。以CNY方程为例，ECT的系数变为负数（-0.0002799693），表明在高阈值状态下，长期均衡关系的偏离对CNY的短期调整具有反向影响。此外，其他解释变量也呈现出与高阈值状态相适应的影响方向和程度。