卷积神经网络（LENET）_class lenet(nn.module): def __init__(self, in_chan

《动手学深度学习pytorch》部分学习笔记，仅用作自己复习。

卷积神经网络（LENET）

多层感知机的从零开始实现⾥我们构造了一个含单隐藏层的多层感知机模型来对Fashion-MNIST数据集中的图像进行分类。每张图像高和宽均是28像素。我们将图像中的像素逐行展开，得到⻓度为784的向量，并输入进全连接层中。然而，这种分类⽅方法有⼀定的局限性。

1. 图像在同⼀列邻近的像素在这个向量中可能相距较远。它们构成的模式可能难以被模型识别。
2. 对于⼤尺⼨的输⼊图像，使⽤全连接层容易造成模型过大。假设输⼊是⾼和宽均为1000像素的彩色 照 片 （ 含 3 个 通 道 ） 。 即使全连接层输出个数仍是256 ， 该 层 权 重 参 数 的 形 状 是3000000×256：它占⽤了大约3 GB的内存或显存。这带来过复杂的模型和过高的存储开销。

卷积层尝试解决这两个问题。

• 一⽅面，卷积层保留输入形状，使图像的像素在高和宽两个方向上的相关性均可能被有效识别。
• 另⼀方⾯，卷积层通过滑动窗⼝将同一卷积核与不同位置的输⼊重复计算，从而避免参数尺⼨过⼤。 

卷积神经网络就是含卷积层的网络。本节⾥我们将介绍⼀个早期⽤来识别⼿写数字图像的卷积神经⽹络：LeNet 。这个名字来源于LeNet论⽂的第⼀作者Yann LeCun。LeNet展示了通过梯度下降训练卷积神经⽹络可以达到手写数字识别在当时最先进的结果。这个奠基性的⼯作第⼀次将卷积神经网络推上舞台，为世⼈所知。LeNet的⽹络结构如下图所示。 

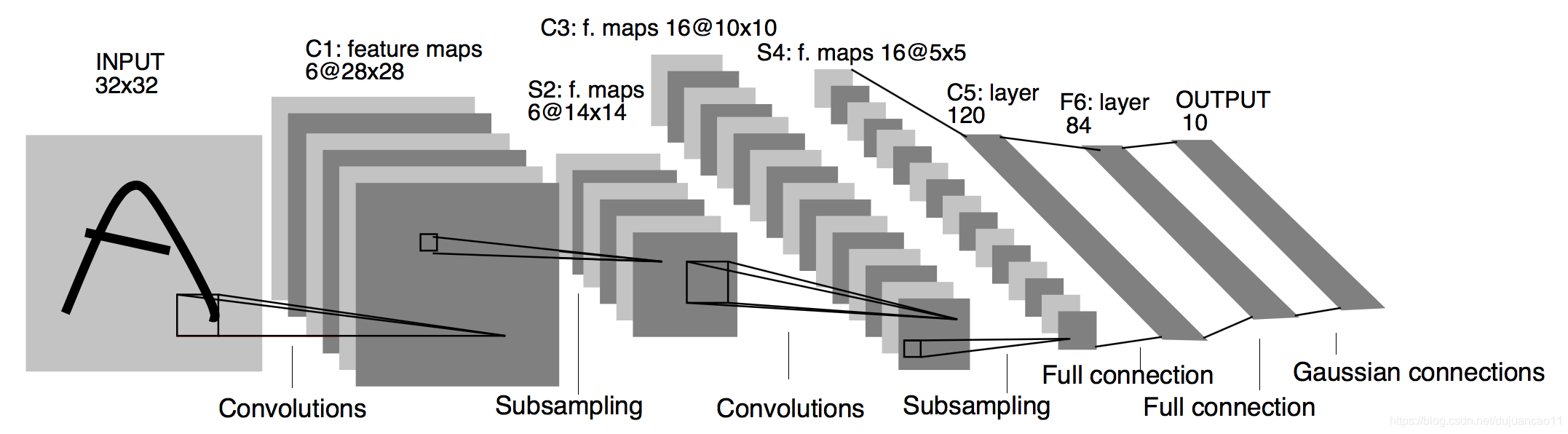
 LENET模型 

LeNet分为卷积层块和全连接层块两个部分。

卷积层块⾥的基本单位是卷积层后接最大池化层：

卷积层用来识别图像里的空间模式，如线条和物体局部，之后的最大池化层则用来降低卷积层对位置的敏感性。卷积层块由两个这样的基本单位重复堆叠构成。在卷积层块中，每个卷积层都使⽤5×5 的窗⼝，并在输出上使用sigmoid激活函数。第⼀个卷积层输出通道数为6，第⼆个卷积层输出通道数则增加到16。这是因为第二个卷积层比第⼀个卷积层的输入的⾼和宽要小，所以增加输出通道使两个卷积层的参数尺⼨类似。卷积层块的两个最大池化层的窗⼝形状均为2×2 ，且步幅为2。由于池化窗⼝与步幅形状相同，池化窗⼝在输入上每次滑动所覆盖的区域互不重叠。

卷积层块的输出形状为(批量⼤小, 通道, 高, 宽)。当卷积层块的输出传⼊全连接层块时，全连接层块会将小批量中每个样本变平（flatten）。也就是说，全连接层的输⼊形状将变成⼆维，其中第一维是小批量中的样本，第二维是每个样本变平后的向量表示，且向量⻓度为通道、⾼和宽的乘积。全连接层块含3个全连接层。它们的输出个数分别是120、84和10，其中10为输出的类别个数。

下⾯通过 Sequential 类来实现LeNet模型。

import time
import torch
from torch import nn, optim
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
device = torch.device('cuda' if torch.cuda.is_available() else
'cpu')
class LeNet(nn.Module):
    def __init__(self):
        # 初始化
        super(LeNet, self).__init__()
        # 卷积层 in_channels, out_channels,kernel_size
        self.conv = nn.Sequential(nn.Conv2d(1, 6, 5), 
        nn.Sigmoid(),
        # kernel_size, stride
        nn.MaxPool2d(2, 2), 
 
        nn.Conv2d(6, 16, 5),
        nn.Sigmoid(),
        nn.MaxPool2d(2, 2)
        )
        # 全连接层 
        self.fc = nn.Sequential(
        nn.Linear(16*4*4, 120),
        nn.Sigmoid(),
        nn.Linear(120, 84),
        nn.Sigmoid(),
        nn.Linear(84, 10)
        )
        # 前向传播
    def forward(self, img):
        feature = self.conv(img)
        output = self.fc(feature.view(img.shape[0], -1))
        return output

查看每个层的形状。

net = LeNet()
print(net)

输出：

LeNet((conv): Sequential(
(0): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(1): Sigmoid()
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1,
ceil_mode=False)
(3): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(4): Sigmoid()
(5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1,
ceil_mode=False)
)
(fc): Sequential(
(0): Linear(in_features=256, out_features=120, bias=True)
(1): Sigmoid()
(2): Linear(in_features=120, out_features=84, bias=True)
(3): Sigmoid()
(4): Linear(in_features=84, out_features=10, bias=True)))

可以看到，在卷积层块中输⼊的⾼和宽在逐层减小。卷积层由于使用⾼和宽均为5的卷积核，从而将⾼和宽分别减小4，而池化层则将⾼和宽减半，但通道数则从1增加到16。全连接层则逐层减少输出个数，直到变成图像的类别数10。

获取数据和训练模型

实验LeNet模型。实验中，我们仍然使⽤Fashion-MNIST作为训练数据集。

batch_size = 256
# 载入输数据集
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

因为卷积神经网络计算⽐多层感知机要复杂，建议使用GPU来加速计算。因此，我们对softmax回归的从零开始实现中描述的 evaluate_accuracy 函数略略作修改，使其⽀持GPU计算。

# 本函数已保存在d2lzh_pytorch包中方便以后使用。
def evaluate_accuracy(data_iter, net, device=None):
    if device is None and isinstance(net, torch.nn.Module):
        # 如果没指定device就使用net的device
        device = list(net.parameters())[0].device
    acc_sum, n = 0.0, 0
    with torch.no_grad():
        for X, y in data_iter:
            if isinstance(net, torch.nn.Module):
                net.eval() # 评估模式, 这会关闭dropout
                acc_sum += (net(X.to(device)).argmax(dim=1) == y.to(device)).float().sum().cpu().item()
                net.train() # 改回训练模式
            else: # 自定义的模型, 不考虑GPU
                if('is_training' in net.__code__.co_varnames): # 如果有is_training这个参数
                    # 将is_training设置成False
                    acc_sum += (net(X, is_training=False).argmax(dim=1) == y).float().sum().item() 
                else:
                    acc_sum += (net(X).argmax(dim=1) == y).float().sum().item() 
            n += y.shape[0]
    return acc_sum / n

对定义的 train_ch3 函数略略作修改，确保计算使用的数据和模型同在内存或显存上。

# 本函数已保存在d2lzh_pytorch包中方便以后使用
def train_ch5(net, train_iter, test_iter, batch_size, optimizer, device, num_epochs):
    net = net.to(device)
    print("training on ", device)
    # 交叉熵损失函数
    loss = torch.nn.CrossEntropyLoss()
    batch_count = 0
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n, start = 0.0, 0.0, 0, time.time()
        for X, y in train_iter:
            X = X.to(device)
            y = y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            optimizer.zero_grad()
            l.backward()
            optimizer.step()
            train_l_sum += l.cpu().item()
            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().cpu().item()
            n += y.shape[0]
            batch_count += 1
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f, time %.1f sec'
              % (epoch + 1, train_l_sum / batch_count, train_acc_sum / n, test_acc, time.time() - start))

# 学习率采⽤0.001
lr, num_epochs = 0.001, 5
# 训练算法使用Adam算法
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
train_ch5(net, train_iter, test_iter, batch_size, optimizer, device,num_epochs)

输出：

training on cuda
epoch 1, loss 0.0072, train acc 0.322, test acc 0.584, time 3.7 sec
epoch 2, loss 0.0037, train acc 0.649, test acc 0.699, time 1.8 sec
epoch 3, loss 0.0030, train acc 0.718, test acc 0.724, time 1.7 sec
epoch 4, loss 0.0027, train acc 0.741, test acc 0.746, time 1.6 sec
epoch 5, loss 0.0024, train acc 0.759, test acc 0.759, time 1.7 sec

小结

• 卷积神经网络就是含卷积层的网络。
• LeNet交替使⽤卷积层和最大池化层后接全连接层来进行图像分类。