过拟合以及常见的解决方式_过拟合问题及解决方案

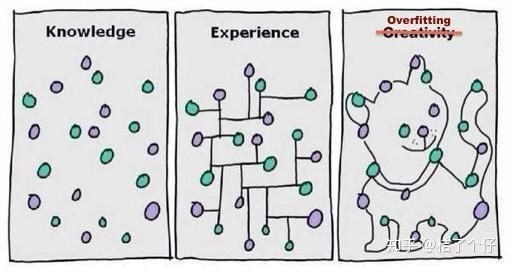
一张可以直观解释的图。

【标准定义】

给定一个假设空间H，一个假设h属于H，如果存在其他的假设h’属于H,使得在训练样例上h的错误率比h’小，但在整个实例分布上h’比h的错误率小，那么就说假设h过度拟合训练数据。

【判断方法】

模型在验证集合上和训练集合上表现都很好，而在测试集合上变现很差。

【常见原因】

1. 学习过度

2. 样本特征不均衡

【细分原因】

1. 训练集的数量级和模型的复杂度不匹配。训练集的数量级要小于模型的复杂度；

2. 训练集和测试集特征分布不一致；

3. 样本里的噪音数据干扰过大，大到模型过分记住了噪音特征，反而忽略了真实的输入输出间的关系；

4. 权值学习迭代次数足够多(Overtraining)，拟合了训练数据中的噪声和训练样例中没有代表性的特征。

【解决方案】

1. simpler model structure

调小模型复杂度，使其适合自己训练集的数量级（缩小宽度和减小深度）

2. data augmentation

训练集越多，过拟合的概率越小。在计算机视觉领域中，增广的方式是对图像旋转，缩放，剪切，添加噪声等。

3. regularization

参数太多，会导致我们的模型复杂度上升，容易过拟合，也就是我们的训练误差会很小。 正则化是指通过引入额外新信息来解决机器学习中过拟合问题的一种方法。这种额外信息通常的形式是模型复杂性带来的惩罚度。 正则化可以保持模型简单，另外，规则项的使用还可以约束我们的模型的特性。

a）L0范数与L1范数

L0范数是指向量中非0的元素的个数。如果我们用L0范数来规则化一个参数矩阵W的话，就是希望W的大部分元素都是0即让参数W是稀疏的。

L1范数是指向量中各个元素绝对值之和，也叫“稀疏规则算子”（Lasso regularization）。为什么L1范数会使权值稀疏？

L1正则为什么更容易获得稀疏解_keep_forward的博客-CSDN博客_为什么l1正则化会产生稀疏解  L1和L2正则常被用来解决过拟合问题。而L1正则也常被用来进行特征选择，主要原因在于L1正则化会使得较多的参数为0，从而产生稀疏解，将0对应的特征遗弃，进而用来选择特征。  但为什么L1正则会产生稀疏解呢？这里利用公式进行解释。 假设只有一个参数为www，损失函数为L(w)L(w)L(w)，分别加上L1正则项和L2正则项后有：JL1(w)=L(w)+λ|w|JL1(w)=L(w)+λ...https://blog.csdn.net/b876144622/article/details/81276818

为什么L0和L1都可以实现稀疏，但常用的为L1？因为L0范数很难优化求解（NP难问题），二是L1范数是L0范数的最优凸近似。

参数稀疏有什么好处？1. 特征选择； 2. 可解释性

b）L2范数

除了L1范数，还有一种更受宠幸的规则化范数是L2范数: ||W||2。它也不逊于L1范数，它有两个美称，在回归里面，有人把有它的回归叫“岭回归”（Ridge Regression），有人也叫它“权值衰减”(weight decay)。 weight decay还有一个好处，它使得目标函数变为凸函数，梯度下降法和L-BFGS都能收敛到全局最优解。

我们让L2范数的规则项||W||2最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。

4. Dropout

在每个训练批次中，通过忽略一半的特征检测器（让一半的隐层节点值为0），可以明显地减少过拟合现象。这种方式可以减少特征检测器（隐层节点）间的相互作用，检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。

Dropout说的简单一点就是：我们在前向传播的时候，让某个神经元的激活值以一定的概率p停止工作，这样可以使模型泛化性更强，因为它不会太依赖某些局部的特征。
 

· 为什么dropout可以解决过拟合？

· 取平均。相当于多个网络分别训练，它们中“相反的过拟合”叠加后会消除。

· 减少神经元之间的共适应关系。字面意思，减少神经元之间的相互依赖，使独立也可以工作。

5. Early stopping

在每一个Epoch结束时（一个Epoch集为对所有的训练数据的一轮遍历）计算validation data的accuracy，当accuracy不再提高时，就停止训练。

一般的做法是，在训练的过程中，记录到目前为止最好的validation accuracy，当连续10次Epoch（或者更多次）没达到最佳accuracy时，则可以认为accuracy不再提高了。此时便可以停止迭代了（Early Stopping）。这种策略也称为“No-improvement-in-n”，n即Epoch的次数，可以根据实际情况取，如10、20、30……