Day13 —— 关联规则分析_关联规则分析 算法

引言

关联规则的经典案例—— 啤酒与尿布

发生在美国沃尔玛连锁超市的真实案例：尿布与啤酒这两种风马牛不相及的商品居然摆在一起，而这也明显增加了这两种商品的销售额。

原来，美国的妇女通常在家照顾孩子，所以她们经常会嘱咐丈夫在下班回家的路上为孩子买尿布，而丈夫在买尿布的同时又会顺手购买自己爱喝的啤酒。

关联规则分析的基本概念

• 事务库

  

上表所示的购物篮数据即是一个事务库，该事务库记录的是用户行为的数据。

• 事务

​ 上表事务库中的每一条记录被称为一笔事务。在购物篮事务中，每一次购物行为即为一笔事务，例如第一行数据“用户1购买商品A,B,C”即为一条事务。

• 项和项集

​ 在购物篮事务中，每样商品代表一个项，项的集合称为项集。每样商品的组合构成项集，例如“A,B”、 “A,C”、 “B,C”、 “A,B,C”都是一个项集，其实也就是不同商品的组合。

• 关联规则

​ 关联规则是形如X → Y的表达式，X称为前件，Y称为后件。

​ 注意X和Y不是指单一的商品，而是指上面提到的项集，比如其形式可以为：{A, B} → {C}，其含义就是如果购买商品A和B的用户也会买C。

• 支持度(Support)

​ 项集的支持度定义为包含该项集的事务在所有事务中所占的比例。

​ 比如项集{A, B} 在购物篮事务中总共出现了3次（第1、2、4条数据），而整个事务库中一共有5条事务，即5条数据，因此项集{A, B}的支持度为3÷5=0.6。

• 频繁项集

​ 支持度大于等于人为设定的阈值（该阈值也称为最小支持度）的项集即为频繁项集，其实也就是指该项集在所有事务中出现的较为频繁。

​ 例如阈值或者说最小支持度设为50%时，因为上面得到项集{A, B}的支持度60%，所以它是频繁项集。

• 置信度(Confidence)

​ 置信度表示在关联规则的先决条件X发生的条件下，关联结果Y发生的概率。

​ 在购物篮事务当中，关联规则X → Y的置信度为购买商品X的基础上购买商品Y的概率P(Y|X)，据公式有：
$$Confidence(X\to Y)=P(Y|X)=\frac{P(X,Y)}{P(X)}$$

• 强关联规则

寻找强关联规则的主要步骤：

1. 先寻找满足最小支持度的频繁项集
2. 在频繁项集中寻找到满足最小置信度的关联规则

• 提升度(Lift)

​ 提升度表示先购买X对Y的概率的提升作用，用来判断规则是否有实际价值，即使用规则后商品在购物车中出现的频率是否高于商品单独出现在购物车中的频率。如果大于1说明规则有效，小于1则无效，等于1则表示X与Y相互独立。

$$Lift(X\to Y)=\frac{P(Y|X)}{P(Y)}=\frac{P(XY)}{P(X)P(Y)}$$

满足最小支持度和最小置信度的规则，叫做“强关联规则”。然而，强关联规则里，又分

为有效的强关联规则和无效的强关联规则。具体划分情况如下：

若Lift(X→Y)>1，则规则“X→Y”是有效的强关联规则。

若Lift(X→Y)<1，则规则“X→Y”是无效的强关联规则。

若Lift(X→Y) =1，则表示X与Y相互独立。

注意：

关联规则分析与协同过滤算法都可以用来作为推荐系统的实现，但仍有区别：

• 协同过滤算法是基于用户或商品之间的距离或相似度进行推荐
• 关联规则分析是通过寻找强关联规则后进行推荐

Apriori算法

Apriori算法简介

关联规则分析的目标是要找出强关联规则，从而实现对目标客户的商品推荐。

Apriori算法是最著名的关联规则的挖掘算法之一，其核心是一种递推算法。

Apriori算法步骤

1. 设定最小支持度和最小置信度
2. 根据最小支持度找出所有的频繁项集
3. 根据最小置信度发现强关联规则

以购物篮数据演示Apriori算法的计算步骤，数据如下所示：

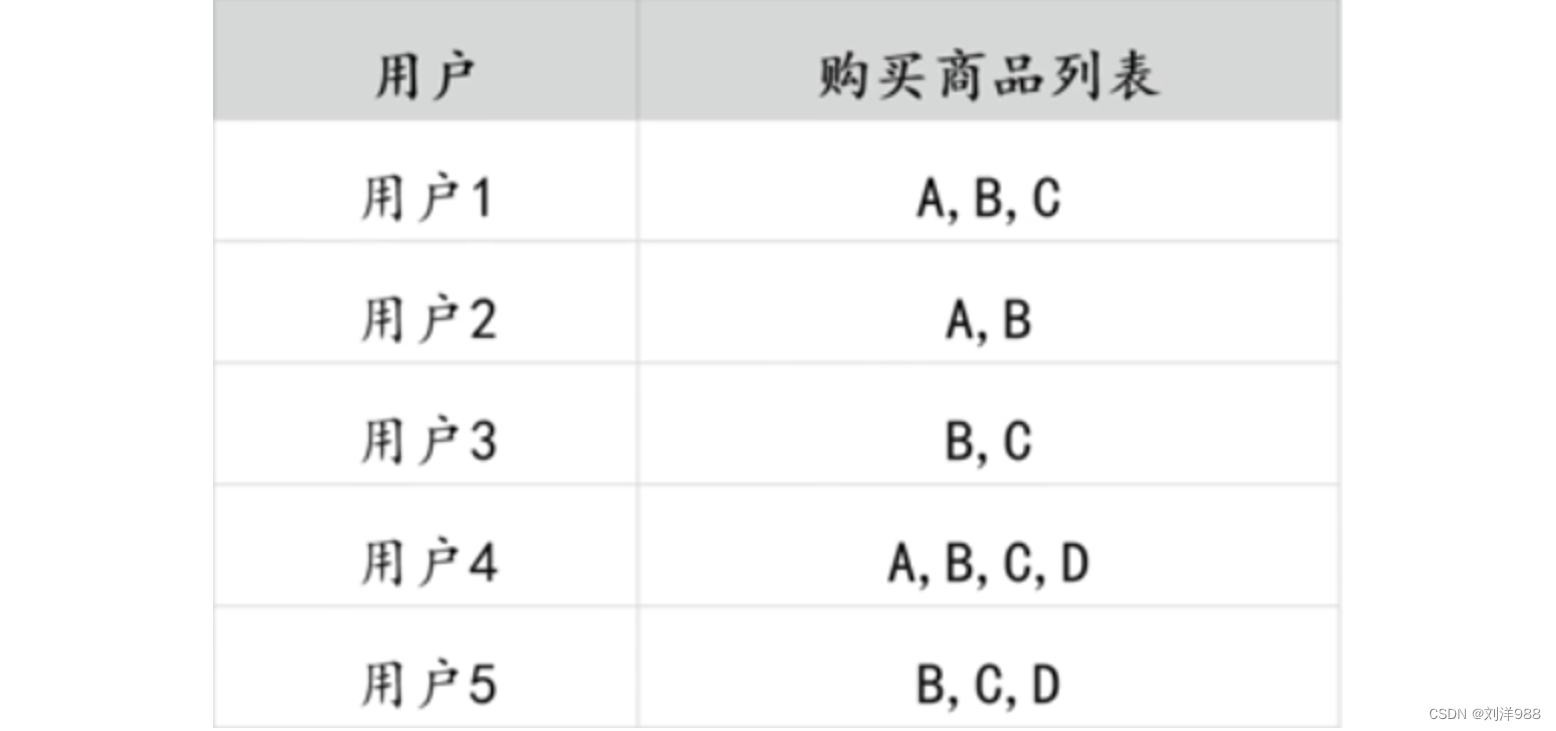
1. 设定最小支持度和最小置信度

   首先设置最小支持度为2/5，也即40%
   其次设置最小置信度为4/5，也即80%

2. 根据最小支持度找出所有的频繁项集

   ​如果某一项集只出现了1次，例如项集{A,B,C,D}，那么其支持度只有1/5，小于最小支持度2/5，其就不是频繁项集，那么也就很难从该项集中挖掘出什么强关联规则，例如就没有理由挖掘出类似{A, B, C} → {D}这样的关联规则。而项集{B, C}出现的次数有4次，其支持度为4/5，属于频繁项集，即商品B和商品C经常同时出现，因此很有可能就能挖掘出{B} → {C}这样的强关联规则（还需要经过步骤三的最小置信度检验）。

   ​Apriori算法采用了一个精巧的思路来加快运算速度：

   ​先计算长度为1的项集，然后挖掘其中的频繁项集；再将长度为1的频繁项集进行排列组合，从中挖掘长度为2的频繁项集，然后以此类推。核心逻辑是一个迭代判断的思想：如果连长度为n-1的项集都不是频繁项集，那就不用考虑长度为n的项集了，例如，如果在迭代的过程发现{A, B, C}不是频繁项集，那么{A, B, C, D}必然不是频繁项集，也就不用去考虑它了。

   首先计算长度为1的候选项集，扫描交易数据集，统计每种商品出现的次数， 如下表所示：

   

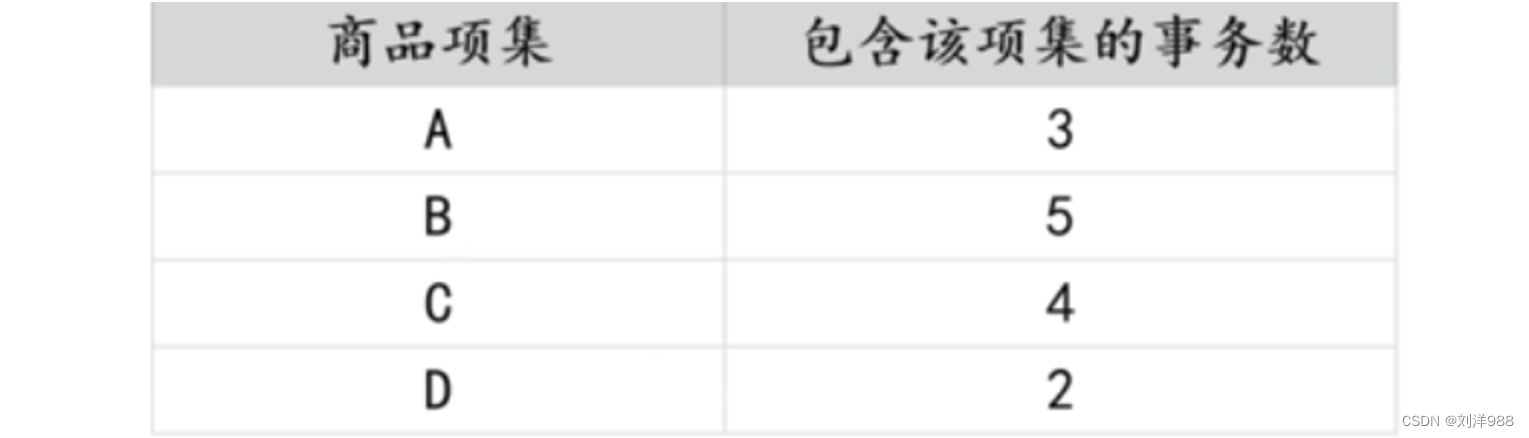
   将长度为1的频繁项集进行两两组合，形成长度为2的候选集，扫描交易数据集，统计各个候选项集在购物篮事务中出现的次数，如下表所示：

   

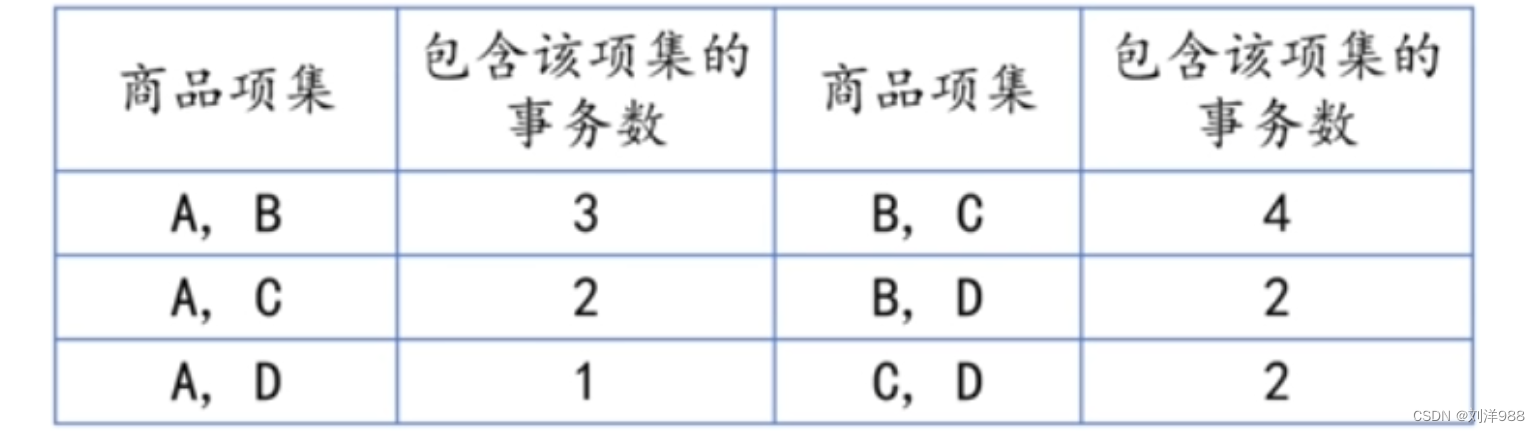
   将长度为2的频繁项集进行两两组合，形成长度为3的候选集，扫描交易数据集，统计各个候选项集在购物篮事务中出现的次数，如下表所示：

   

   两个数据之间，所以我们需要选择长度大于1的频繁项集，长度大于1的所有频繁项集，如下表所示：

   

3. 根据最小置信度发现强关联规则
   ​
   举例：
   {A, B, C}是频繁项集，那么能否得出{B, C} → {A}这样的强关联规则呢？答案是否定的。
   因为{A, B, C}在所有5次事务中共出现2次，而{B, C}共出现4次，所以{B, C} → {A}这条关联规则的置信度为2÷4=0.5，也可以通过公式(2/5)÷(4/5)=0.5进行计算。该置信度说明了当用户买了商品B和C的时候，只有50%的概率会买A（而设置的最小置信度为80%），所以{B, C} → {A}不是一条强关联规则。
   本例中，最终的强关联规则是：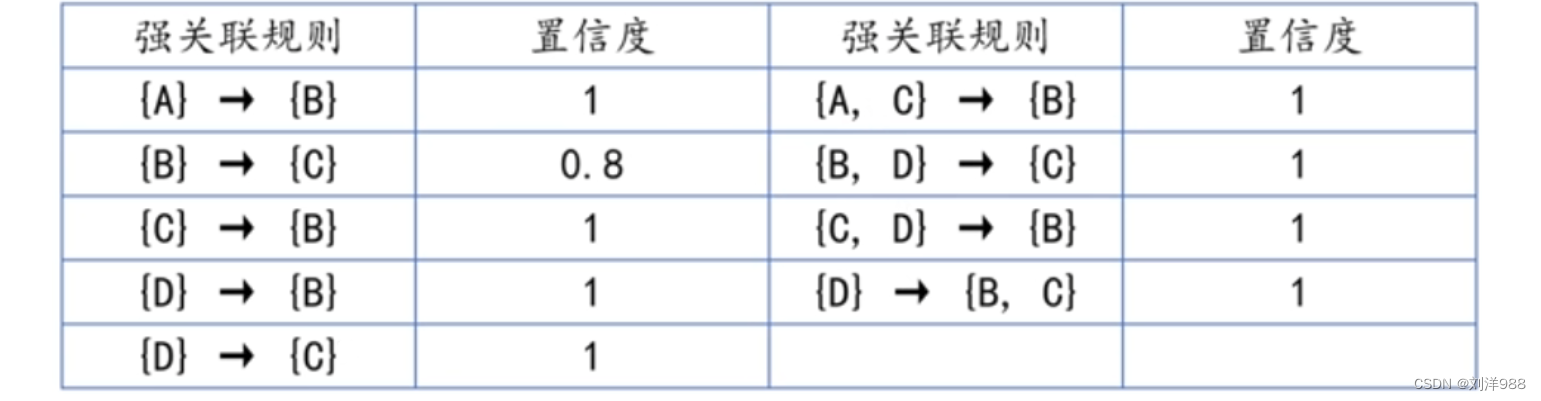

   

Apriori算法的代码实现

命令行安装：

pip install apyori==1.1.2

Jupyter notebook安装：

!pip install apyori==1.1.2

Apriori算法的实现

transactions = [['A', 'B', 'C'], ['A', 'B'], ['B', 'C'], ['A', 'B', 'C', 'D'], ['B', 'C', 'D']]

from apyori import apriori
# 调用apriori函数，指定最小支持度和最小置信度
rules = apriori(transactions, min_support=0.4, min_confidence=0.8)
# 将生成器对象转化成列表
results = list(rules)

for i in results:  # 遍历results中的每一个频繁项集
    for j in i.ordered_statistics:  # 获取频繁项集中的关联规则
        X = j.items_base  # 关联规则的前件
        Y = j.items_add  # 关联规则的后件
        x = ', '.join([item for item in X])  # 连接前件中的元素
        y = ', '.join([item for item in Y])  # 连接后件中的元素
        if x != '':  # 防止出现关联规则前件为空的情况
            print(x + ' → ' + y)  # 通过字符串拼接的方式更好呈现结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

中医病症关联规则分析

背景介绍

​ 中医病案的各种症状是一个错综复杂的整体，但其中也有着密不可分的联系。通过对中医病症之间关系的分析，从而认识疾病的发生发展规律，掌握疾病的诊疗特点，并且获得治疗疾病的最适宜药方。而关联规则分析在寻找中医病因病机、病症之间的关系上发挥了巨大的作用，在挖掘病症之间的关联关系方面应用广泛且实用。

代码实现

import pandas as pd
df = pd.read_excel('中医病症.xlsx')

# 转换为双重列表结构
symptoms = []
for i in df['病人症状'].tolist():
    symptoms.append(i.split(','))
    
# 通过apyori库来实现Apriori算法
from apyori import apriori
rules = apriori(symptoms, min_support=0.1, min_confidence=0.7)
results = list(rules)

for i in results:  # 遍历results中的每一个频繁项集
    for j in i.ordered_statistics:  # 获取频繁项集中的关联规则
        X = j.items_base  # 关联规则的前件
        Y = j.items_add  # 关联规则的后件
        x = ', '.join([item for item in X])  # 连接前件中的元素
        y = ', '.join([item for item in Y])  # 连接后件中的元素
        if x != '':  # 防止出现关联规则前件为空的情况
            print(x + ' → ' + y)  # 通过字符串拼接的方式更好呈现结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21