MIMO系统中的线性处理: 匹配滤波、迫零滤波与维纳滤波_mimo雷达匹配滤波

前言

这篇博客是对经典论文 Linear Transmit Processing in MIMO Communications Systems的摘记。这篇文章考虑的是收发端的各自独立信号处理设计，而非联合设计。继而，给出了匹配滤波、迫零滤波与维纳滤波这三种常见滤波方式的具体数学形式。

系统模型

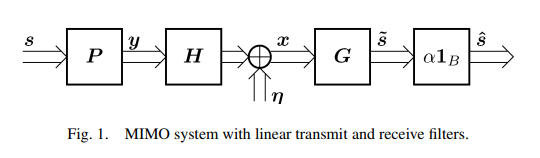
考虑如图所示的一个线性系统模型， 有：
$$\begin{gathered} \mathbf{y}=\mathbf{P}\mathbf{s}\in {\mathbb{C}}^N \\ \tilde{\mathbf{s}}=\mathbf{G}(\mathbf{H}\mathbf{P}\mathbf{s}+\mathbf{\eta })\in {\mathbb{C}}^B \end{gathered}$$
$B$代表了数据流数。$N$代表发送天线数，$M$代表接收天线数。需要解释的是， 最后的方框中的$\alpha 1_B$是指将$\tilde{\mathbf{s}}$乘上一个标量实数$\alpha$，这对系统性能并不会有任何影响，但会影响发射机的设计，后面将会揭示。
同时，定义平均发送能量为：
$$\mathrm{E}\left[\Vert \mathbf{y}{\Vert }_2^2\right]=\mathrm{E}\left[\Vert \mathbf{P}\mathbf{s}{\Vert }_2^2\right]=\mathrm{tr}\left(\mathbf{P}{\mathbf{R}}_{\mathbf{s}}{\mathbf{P}}^{\mathrm{H}}\right)=E_{\mathrm{t}\mathrm{r}}\cdot$$
信噪比可以定义为 （平均了流数与接收天线数）：
$$\gamma =\frac{E_{\mathrm{t}\mathrm{r}}/B}{\mathrm{tr}\left({\mathbf{R}}_{\mathbf{\eta }}\right)/M}$$
其中${\mathbf{R}}_{\mathbf{\eta }}$代表噪声的协方差矩阵。

接收滤波

接收匹配滤波

Receive matched filter (RxMF)
RxMF 旨在最大化滤波器$G$的输出信噪比，这在噪声极大的场景下是最优的。具体地：
$${\mathbf{G}}_{\mathrm{M}\mathrm{F}}={\mathrm{argmax}}_G\frac{{\left|\mathrm{E}\left[{\mathbf{s}}^{\mathrm{H}}\tilde{\mathbf{s}}\right]\right|}^2}{\mathrm{E}\left[\Vert {\mathbf{G}\mathbf{\eta }|}_2^2\right]}$$
分子中，通过作相关，提取出处理后信号中包含真实信号信息的能量值，去除掉噪声。 分母则是经过滤波后的噪声能量。因此通过对上式求导置0，得到：
$${\mathbf{G}}_{\mathrm{M}\mathrm{F}}={\alpha }^{\prime }{\mathbf{R}}_{\mathbf{s}}{\mathbf{P}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}{\mathbf{R}}_{\mathbf{\eta }}^{-1}\in {\mathbb{C}}^{B\times M}$$
其中，${\alpha }^{\prime }$为标量可以任意选取，并不影响接收信噪比， 因此后文中可置为1. 相关简要推导放在了附录中。观察可以看到， 接收信号抵达接收端时经历了$HP$,则对其的处理就是其转置$P^H{H}^H$。

接收迫零滤波

Receive Zero-Forcing Filter （RxZF)
迫零均衡的思路很简单，假定没有噪声，令处理后信号与原信号相等。也即:
$${\tilde{\mathbf{s}}|}_{\eta =0_M}=\mathbf{G}\mathbf{H}\mathbf{P}\mathbf{s}\equiv \mathbf{s}$$
因此，$GHP$应为单位阵。
$$\mathrm{E}\left[\Vert \mathbf{s}-\tilde{\mathbf{s}}{\Vert }_2^2\right]=\mathrm{E}\left[\Vert G\mathbf{\eta }{\Vert }_2^2\right]$$
因此，RxZF的推导可以通过求解如下问题：
$${\mathbf{G}}_{\mathrm{Z}\mathrm{F}}={\mathrm{argmin}}_{\mathbf{G}}\mathrm{E}\left[\Vert \mathbf{G}\mathbf{\eta }{\Vert }_2^2\right]\text{ s.t.: }\mathbf{G}\mathbf{H}\mathbf{P}=1_B$$
$1_B$就是单位阵。该问题可以通过拉格朗日乘子法求解，过程也放在了附录之中。最优解为：
$${\mathbf{G}}_{\mathrm{Z}\mathrm{F}}={\left({\mathbf{P}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}{\mathbf{R}}_{\mathbf{\eta }}^{-1}\mathbf{H}\mathbf{P}\right)}^{-1}{\mathbf{P}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}{\mathbf{R}}_{\mathbf{\eta }}^{-1}\in {\mathbb{C}}^{B\times M}.$$
相较于匹配滤波，这里多了一项${\mathbf{G}}_{\mathrm{Z}\mathrm{F}}={\left({\mathbf{P}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}{\mathbf{R}}_{\mathbf{\eta }}^{-1}\mathbf{H}\mathbf{P}\right)}^{-1}$，因此迫零滤波可以理解为是匹配滤波后再做了一步干扰消除。当${\mathbf{R}}_{\mathbf{\eta }}$为单位阵 (或单位阵乘上标量）时，原式就退化为${\mathbf{G}}_{\mathrm{Z}\mathrm{F}}={\left({\mathbf{P}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}\mathbf{H}\mathbf{P}\right)}^{-1}{\mathbf{P}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}$。

接收维纳滤波

Receive Wiener Filter （RxWF）
维纳滤波器旨在最小化MSE值，也即:
$${\mathbf{G}}_{\mathrm{W}\mathrm{F}}={\mathrm{argmin}}_{\mathbf{G}}\mathrm{E}\left[\Vert \mathbf{s}-\tilde{\mathbf{s}}{\Vert }_2^2\right]$$
令导数为0，可以得到：
$${\mathbf{G}}_{\mathrm{W}\mathrm{F}}={\left({\mathbf{P}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}{\mathbf{R}}_{\mathbf{\eta }}^{-1}\mathbf{H}\mathbf{P}+{\mathbf{R}}_{\mathbf{s}}^{-1}\right)}^{-1}{\mathbf{P}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}{\mathbf{R}}_{\mathbf{\eta }}^{-1}$$
这里运用到了矩阵求逆引理，详见附录。注意到， 当信噪比较低时，${\left({\mathbf{P}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}{\mathbf{R}}_{\mathbf{\eta }}^{-1}\mathbf{H}\mathbf{P}+{\mathbf{R}}_{\mathbf{s}}^{-1}\right)}^{-1}$退化为${\mathbf{R}}_{\mathbf{s}}$，维纳滤波器退化为匹配滤波。当信噪比较高时，退化为迫零滤波。

发送滤波

发送匹配滤波

类似地，可以通过如下优化问题求解：
$${\mathbf{P}}_{\mathrm{M}\mathrm{F}}={\mathrm{argmax}}_{\mathbf{P}}\frac{{\left|\mathrm{E}\left[{\mathbf{s}}^{\mathrm{H}}\tilde{\mathbf{s}}\right]\right|}^2}{\mathrm{E}\left[\Vert \mathbf{G}\mathbf{\eta }|{|}_2^2\right]}\text{ s.t.: }\mathrm{E}\left[\Vert \mathbf{P}\mathbf{s}{\Vert }_2^2\right]=E_{\mathrm{t}\mathrm{r}}$$
这比接收滤波要容易求解因为分母是一个常数，直接通过拉格朗日乘子法可以得到：
P M F = β T x M F H H G H ∈ C N × B β T x M F = E t r tr ⁡ ( H H G H R s G H )

$$\begin{aligned} \boldsymbol{P}_{\mathrm{MF}} &=\beta_{\mathrm{TxMF}} \boldsymbol{H}^{\mathrm{H}} \boldsymbol{G}^{\mathrm{H}} \in \mathbb{C}^{N \times B} \\ \beta_{\mathrm{TxMF}} &=\sqrt{\frac{E_{\mathrm{tr}}}{\operatorname{tr}\left(\boldsymbol{H}^{\mathrm{H}} \boldsymbol{G}^{\mathrm{H}} \boldsymbol{R}_{\mathbf{s}} \boldsymbol{G H}\right)}} \end{aligned}$$ PMF​βTxMF​​=βTxMF​HHGH∈CN×B=tr(HHGHRs​GH)Etr​​ ​​
可以看到，发送匹配滤波和接收匹配滤波一样，都是信号接下来要经过的线性变换的共轭转置。

发送迫零滤波

与接收迫零滤波不同的时，此时除了令$GHP$为单位阵外，也期望最小化发送功率，因此优化问题可以表示为：
$${\tilde{\mathbf{P}}}_{\mathrm{Z}\mathrm{F}}={\mathrm{argmin}}_{\mathbf{P}}\mathrm{E}\left[\Vert \mathbf{P}\mathbf{s}{\Vert }_2^2\right]\text{ s.t.: }\mathbf{G}\mathbf{H}\mathbf{P}=1_B$$
通过拉格朗日乘子法可以得到：
$${\tilde{\mathbf{P}}}_{\mathrm{Z}\mathrm{F}}={\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}{\left(\mathbf{G}\mathbf{H}{\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}\right)}^{-1}\in {\mathbb{C}}^{N\times B}.$$
然而这一解并不一定能满足功率约束。因此一种直觉的做法就是引入一个常数标量进行归一化。即：
$${\mathbf{P}}_{\mathrm{Z}\mathrm{F}}={\beta }_{\mathrm{T}\mathrm{x}\mathrm{Z}\mathrm{F}}{\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}{\left(\mathbf{G}\mathbf{H}{\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}\right)}^{-1}\in {\mathbb{C}}^{N\times B}$$
其中，
$${\beta }_{\mathrm{T}\mathrm{x}\mathrm{Z}\mathrm{F}}=\sqrt{\frac{E_{\mathrm{t}\mathrm{r}}}{\mathrm{tr}((\mathbf{G}\mathbf{H}{\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}{)}^{-1}{\mathbf{R}}_{\mathbf{s}})}}$$

发送维纳滤波

假如仍以基本的MMSE为目标，维纳滤波的解由下式给出:
$${\mathbf{P}}_{\mathrm{C}\mathrm{M}\mathrm{M}\mathrm{S}\mathrm{E}}={\mathrm{argmin}}_{\mathbf{P}}\mathrm{E}\left[\Vert \mathbf{s}-\tilde{\mathbf{s}}{\Vert }_2^2\right]\text{ s.t.: }\mathrm{E}\left[\Vert \mathbf{P}\mathbf{s}{\Vert }_2^2\right]\le E_{\mathrm{t}\mathrm{r}}\cdot$$
其解为：
$${\mathbf{P}}_{\mathrm{C}\mathrm{M}\mathrm{M}\mathrm{S}\mathrm{E}}={\left({\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}\mathbf{G}\mathbf{H}+\lambda 1_N\right)}^{-1}{\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}\in {\mathbb{C}}^{N\times B}$$
其中$\lambda$为拉格朗日乘子，用以满足功率约束。然而问题来了，此时发现$\lambda$只与发送功率有关。当发送功率较大但噪声功率更大的低信噪比情况下，维纳滤波器仍会迫近与迫零滤波。根据push-through公式，有：
$${\left({\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}\mathbf{G}\mathbf{H}+\lambda 1_N\right)}^{-1}{\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}={\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}{\left(\mathbf{G}\mathbf{H}{\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}+\lambda 1_N\right)}^{-1}$$
也就是说，这样的滤波器并不具备考虑噪声的能力。

因此，进行改进，求解如下问题：
{ P W F , β T x W F } = argmin ⁡ { P , β } E [ ∥ s − β − 1 s ~ ∥ 2 2 ]  s.t.:  E [ ∥ P s ∥ 2 2 ] = E t r .

$$\begin{aligned} \left\{\boldsymbol{P}_{\mathrm{WF}}, \beta_{\mathrm{TxWF}}\right\} &=\operatorname{argmin}_{\{\boldsymbol{P}, \beta\}} \mathrm{E}\left[\left\|\boldsymbol{s}-\beta^{-1} \tilde{\boldsymbol{s}}\right\|_{2}^{2}\right] \\ \text { s.t.: } \mathrm{E}\left[\|\boldsymbol{P} \boldsymbol{s}\|_{2}^{2}\right] &=E_{\mathrm{tr}} . \end{aligned}$$ {PWF​,βTxWF​} s.t.: E[∥Ps∥22​]​=argmin{P,β}​E[∥∥​s−β−1s~∥∥​22​]=Etr​.​
引入了标量因子$\beta$，可以理解为接收机要将最后得到的信号除以$\beta$。那么，$\beta$将是越大越好的。因为如果发送滤波得到了更大的$\beta$，意味着最后除掉时将噪声的能量也降低了。因此，问题成了寻找满足上述优化问题的$P$和最大的$\beta$，通过拉格朗日乘子法，得到：
$${\mathbf{P}}_{\mathrm{W}\mathrm{F}}={\beta }_{\mathrm{T}\mathrm{x}\mathrm{W}\mathrm{F}}{\mathbf{F}}^{-1}{\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}\in {\mathbb{C}}^{N\times B}$$
and
$${\beta }_{\mathrm{T}\mathrm{x}\mathrm{W}\mathrm{F}}=\sqrt{\frac{E_{\mathrm{t}\mathrm{r}}}{\mathrm{tr}\left({\mathbf{F}}^{-2}{\mathbf{H}}^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}{\mathbf{R}}_{\mathbf{s}}\mathbf{G}\mathbf{H}\right)}}$$
where we defined
$$\mathbf{F}=H^{\mathrm{H}}{\mathbf{G}}^{\mathrm{H}}\mathbf{G}H+\frac{\mathrm{tr}\left(\mathbf{G}{\mathbf{R}}_{\eta }{\mathbf{G}}^{\mathrm{H}}\right)}{E_{\mathrm{t}\mathrm{r}}}{1}_N\in {\mathbb{C}}^{N\times N}$$
可以看到，它与不引入$\beta$时的维纳滤波的差别在于，此时没有了拉格朗日乘子，且解与信噪比直接相关。

性能结果

附录

接收匹配滤波推导

接收迫零滤波推导

接收维纳滤波推导

其中的求逆公式参照博客： https://zhuyulab.blog.csdn.net/article/details/118761178?spm=1001.2014.3001.5502