- 1Android14 适配之——targetSdkVersion 升级到 34 需要注意些什么
- 2蚁剑与一句话木马_蚁剑一句话
- 3c语言根据数组创建二叉排序树_数组构造二叉排序树代码
- 4Matlab无人机三维路径规划|基于A_Star算法实现复杂地形下无人机威胁概率地图最短路径避障三维航迹规划研究_matlab无人机航迹规划
- 5微软云服务器搭建,如何配置云服务(经典) | Microsoft Docs
- 6二叉树、B树、B+树、红黑树 的 本质区别以及各个应用场景_数据结构中,链表,b树,b+树,红黑树区别
- 7【SPIE出版-往届均已见刊检索 EI、SCOPUS双检索 | 高录用-稳定检索 | ISSN已确定(ISSN: 0277-786X)】第四届先进算法与信号图像处理国际学术会议(AASIP 2024)
- 8【Golang】Json 无法表示 float64 类型的 NaN 以及 Inf 导致的 panic_golang float nan
- 9华为OD机试C卷-- 最长子字符串的长度(二)(Java & JS & Python & C)
- 10android 快速修改包名步骤_namespace动态修改应用包名
哈夫曼编码与解码课程设计
赞
踩
目录
源码:哈夫曼编码与解码源码
本学期期末数据结构的课程设计,作者抽到的题目是哈夫曼编码与解码,为了方便有需要的友友做出更好的设计,这里写下我的做法,供大家参考。

效果演示:
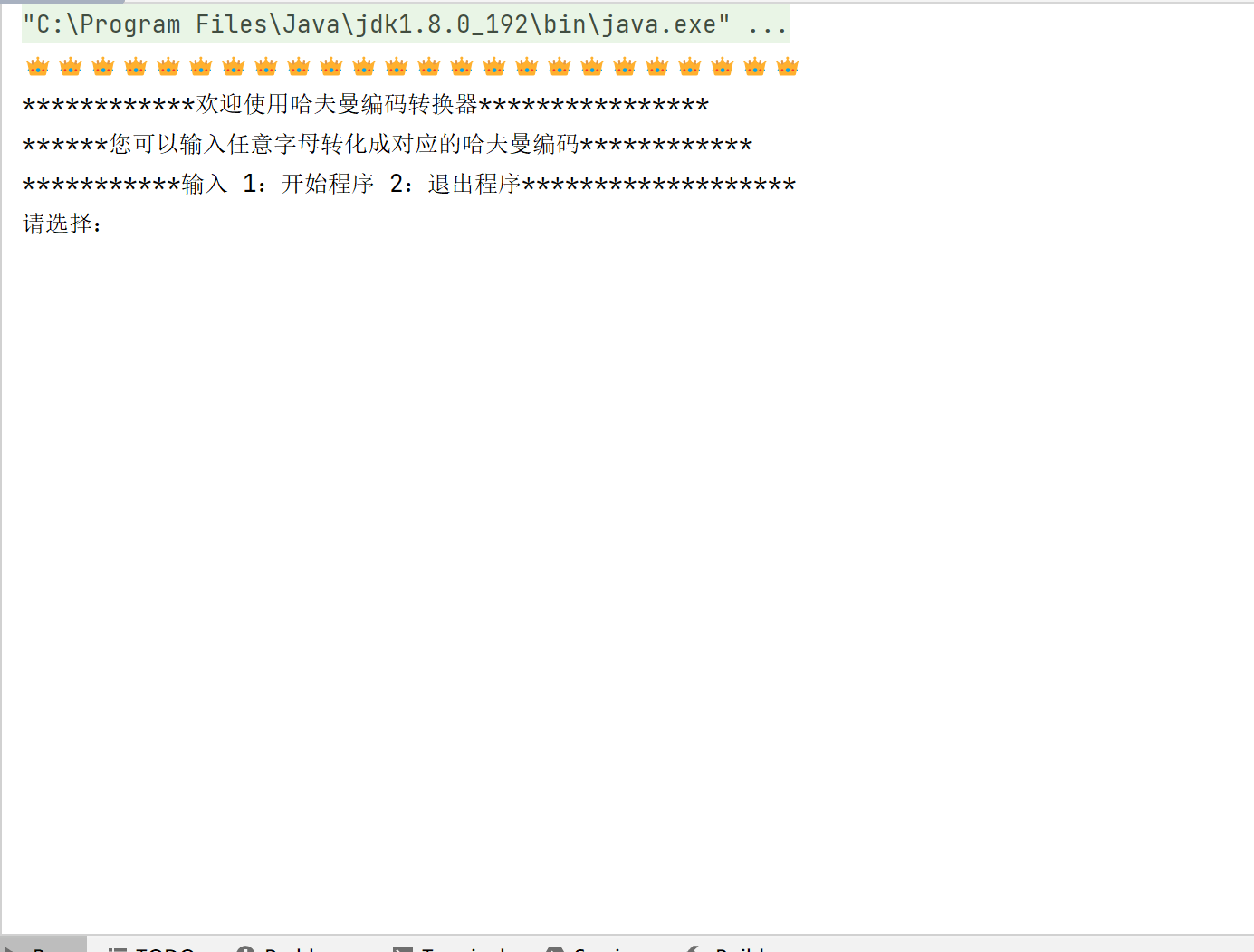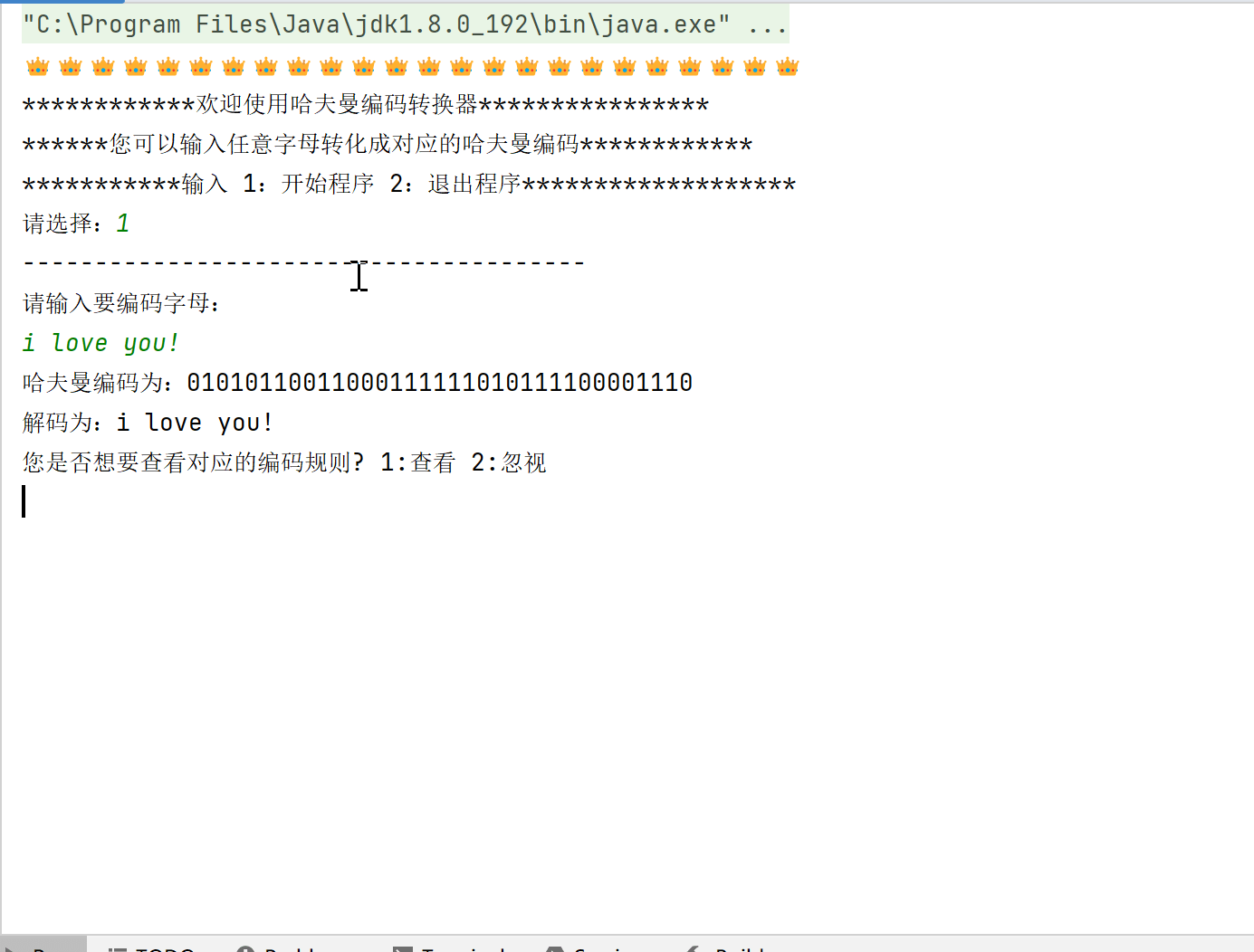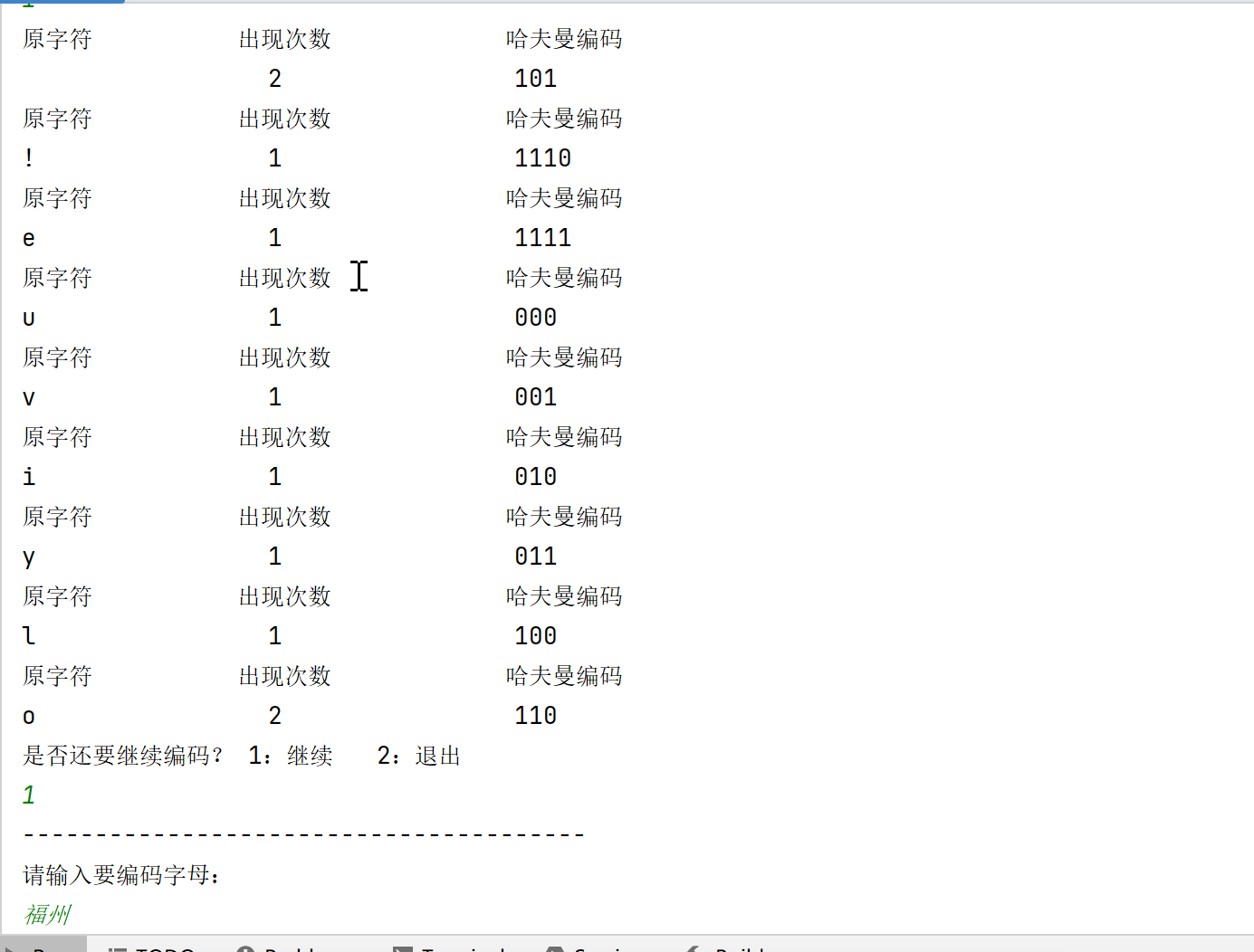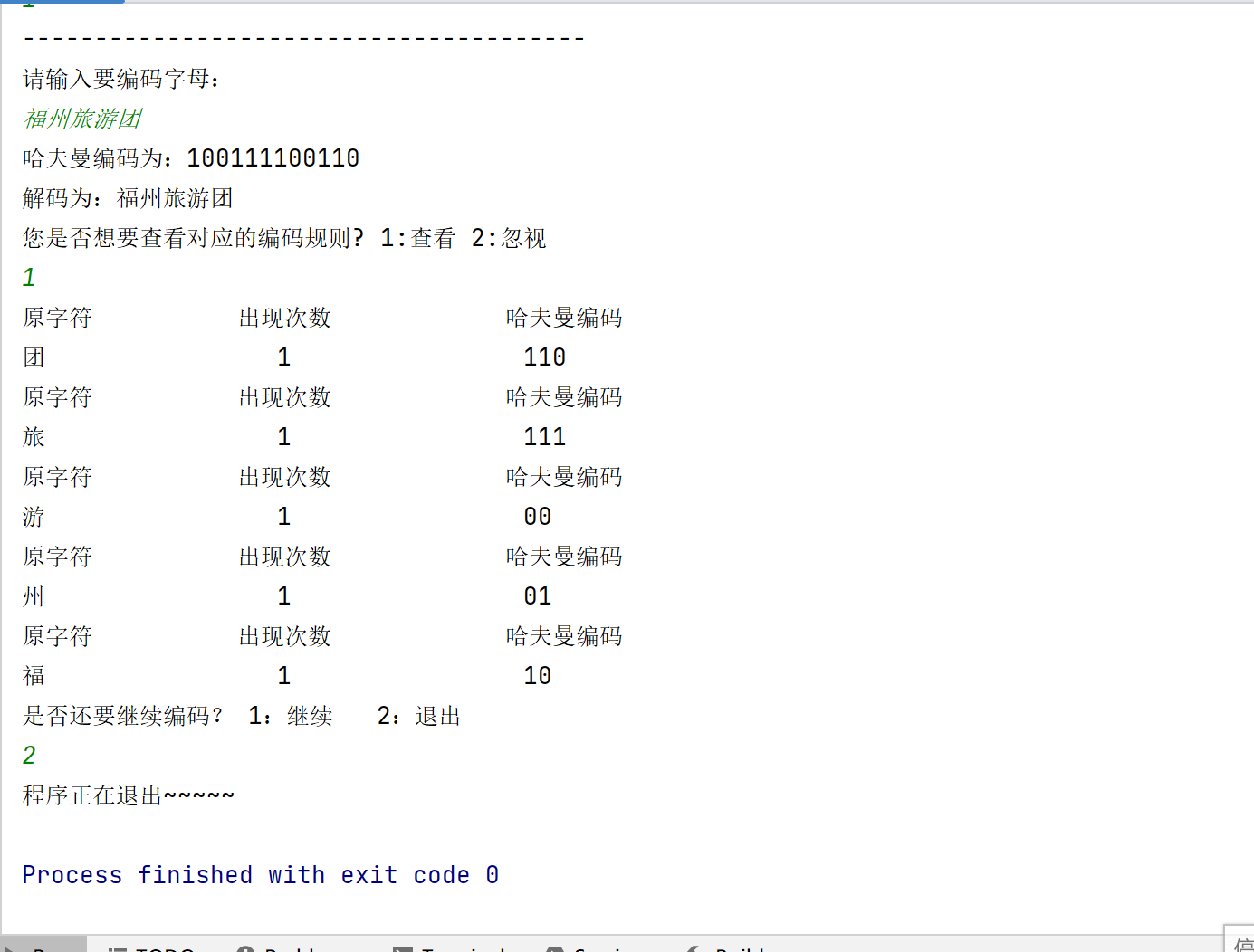
一、问题描述
1.1 课程设计目的:
程序设计课程的主要目的包括以下几个方面:1. 培养编程思维:让学生学会用逻辑和结构化的方式思考问题,能够将复杂的任务分解成可管理的步骤。2. 掌握编程技能:比如能够用特定编程语言实现数据处理、算法实现等。3. 提高问题解决能力:面对各种实际问题,能够运用编程知识和思维来找到解决方案。4. 培养创新能力:鼓励学生通过编程来创造新的工具、应用或解决方案。5. 增强计算机素养。6.为后续学习和职业发展奠定基础:无论是在计算机相关领域进一步深造,还是从事软件开发等职业,都提供了必要的基础。
1.2 课程设计任务:
哈夫曼编码是一种可变字长编码方式,由大卫·哈夫曼于 1952 年提出。它的主要目的是根据字符出现的概率来构造平均长度最短的码字,从而实现数据的无损压缩。例如,对于一个包含大量重复字符的文本,哈夫曼编码可以使这些高频字符的编码很短,从而节省大量存储空间。
基本要求:测试数据为任意一段完整的英文,也可以是一段完整的中文;采用哈夫曼算法进行编码; 可输出对应字符编码的解码。
二、设计过程
2.1 设计思想(数据结构):
在实现哈夫曼编码的过程中,运用到了哈希表和哈夫曼树的数据结构。下面是对应其对应数据结构的相关理论。
• 哈希表(Hash table)是一种数据结构,它通过哈希函数将键映射到表中的位置来访问记录。它通过把关键码值映射到表中一个位置来访问记录,以加快查找速度。
• 哈夫曼树(Huffman Tree)是一种带权路径长度最短的二叉树,通常用于数据压缩中。它通过频率来构建树结构,频率越高的字符越靠近根部,以实现更高效的编码和解码过程。
2.2 设计表示(函数说明):
使用函数对代码的部分功能进行封装。
• createHT:来实现构建哈夫曼树。将每个节点都构成一颗只有一个根节点的二叉树,从当前的二叉树集合中选择权值最小的两颗二叉树,将它们合并成一颗新的二叉树,合并的方式是将这两颗二叉树作为新二叉树的左右子树,新二叉树的根节点的权值为这两颗子树的根节点权值之和。最后将上述操作进行重复合并。
• CreateHCode:配合哈希表存储的编码规则来完成哈夫曼编码。
• tranFor:进行哈夫曼编码,配合字符串算法,进行字母串的匹配和替换。哈夫曼编码保证编码出来的字符串长度较优。
• unTranFor:进行解码,将二进制数翻译成对应的字母。哈夫曼解码的关键是正确构建哈夫曼树和解码规则。在编码过程中,每个字符都被分配了一个唯一的编码,而在解码过程中,需要根据这些编码来还原原始字符。需要注意的是,哈夫曼解码需要知道编码时使用的哈夫曼树和编码规则,否则无法正确解码。因此,在实际应用中,通常需要将哈夫曼树和编码规则与编码数据一起存储或传输,以便在解码时使用。
• main:主函数,将各个模块总结起来,实现哈夫曼编码的各种逻辑,拼接。
• Menu:菜单函数:用来提示用户输入输出,及该程序的使用手册。
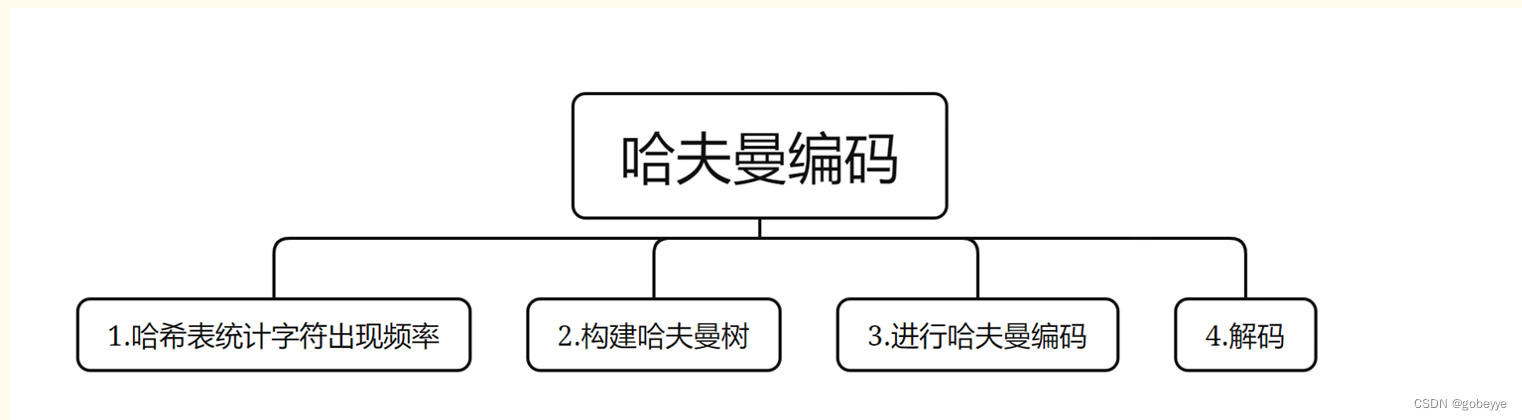
2.3 详细设计(主要算法):
首先读入相应的数据,采用哈希表来存储,字母及其出现的频率,方便后续编码。接着使用 createHT 构建哈夫曼树算法来构建哈夫曼树。同时利用哈夫曼树来生成哈夫曼编码,哈夫曼编码的规则采用另一个哈希表单独存储,最后再遍历一遍读入的字符,运用哈夫曼编码的对应规则来进行字符串编码。最后根据哈夫曼编码是一种无前缀编码,所以在解码时不会混淆,既能保证长度够小,又能保证解码时不会出错,可见哈夫曼编码是一种非常优秀的编码。下面是哈夫曼编码与解码的模块图。哈夫曼流程图(下面这张图是贴在任务书里面的,为了方便大家所以把这张图一起贴过来了)。
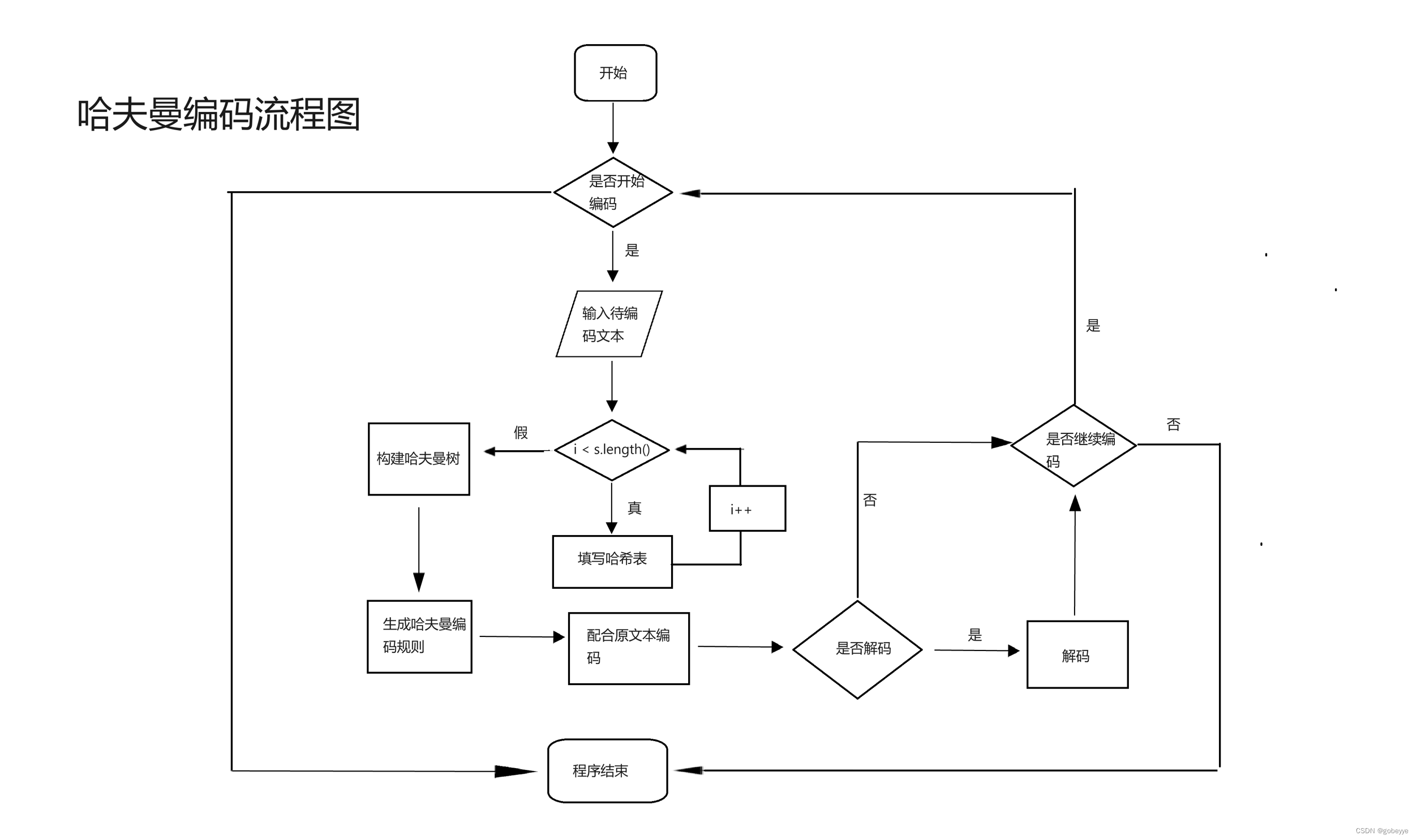
2.4 用户手册(使用说明):
该程序的主要作用是:输入对应数据,程序会将数据转化成哈夫曼编码,同时还会询问用户是否需要查看编码规则,如果需要则输出对应的编码规则,最后会再询问用户是否要选择退出,保证可以进行多次输入输出。哈夫曼编码在数据压缩、加密解密等领域都有广泛的应用。例如,在文件压缩中,哈夫曼编码可以将文件中的字符转换为较短的编码,从而减小文件的大小;在通信中,哈夫曼编码可以用于压缩数据,提高传输效率。
三、测试报告
3.1 测试用例:
• 中文示例:
其实生活中本没有那么多烦恼,一切只不过是庸人自扰。只要我们稍微停下脚步,就可以更好地珍惜生命本原的美丽,不为爱欲所炫目,不为污秽所恶心,永远正确看待生命,永远那么透明地看。那时候,你将发现,在人生的幽僻处、细小处,都闪耀着光芒。
• 英文示例:
We all stood there under the awning and just inside the door of the Wal-Mart. We all waited, some patiently, others irritated, because nature messed up their hurried day. I am always mesmerized by rainfall. I get lost in the sound and sight of the heavens washing away the dirt and dust of the world. Memories of running, splashing so carefree as a child come pouring in as a welcome reprieve from the worries of my day.
3.2 测试结果:
• 中文结果:
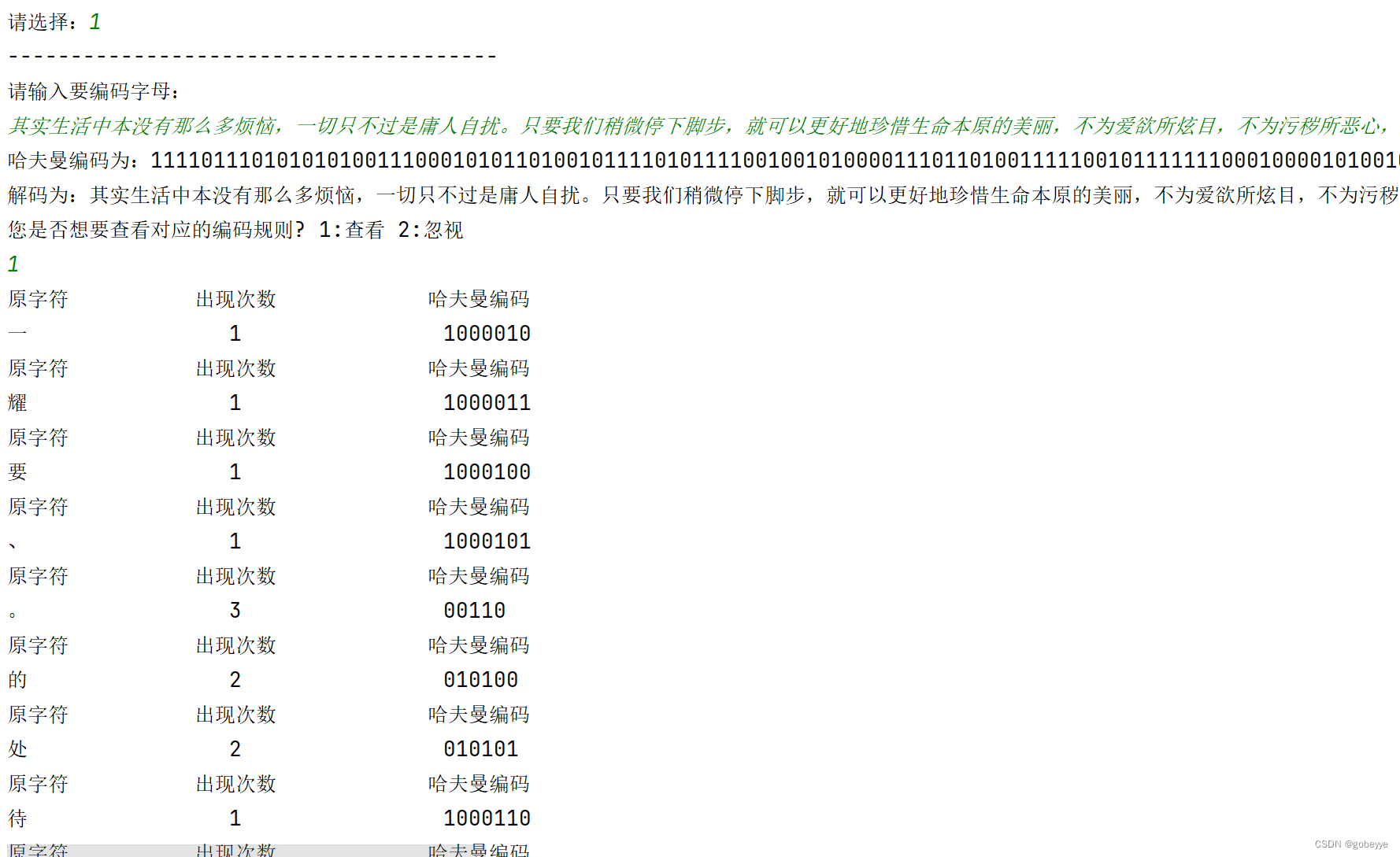
• 英文结果:
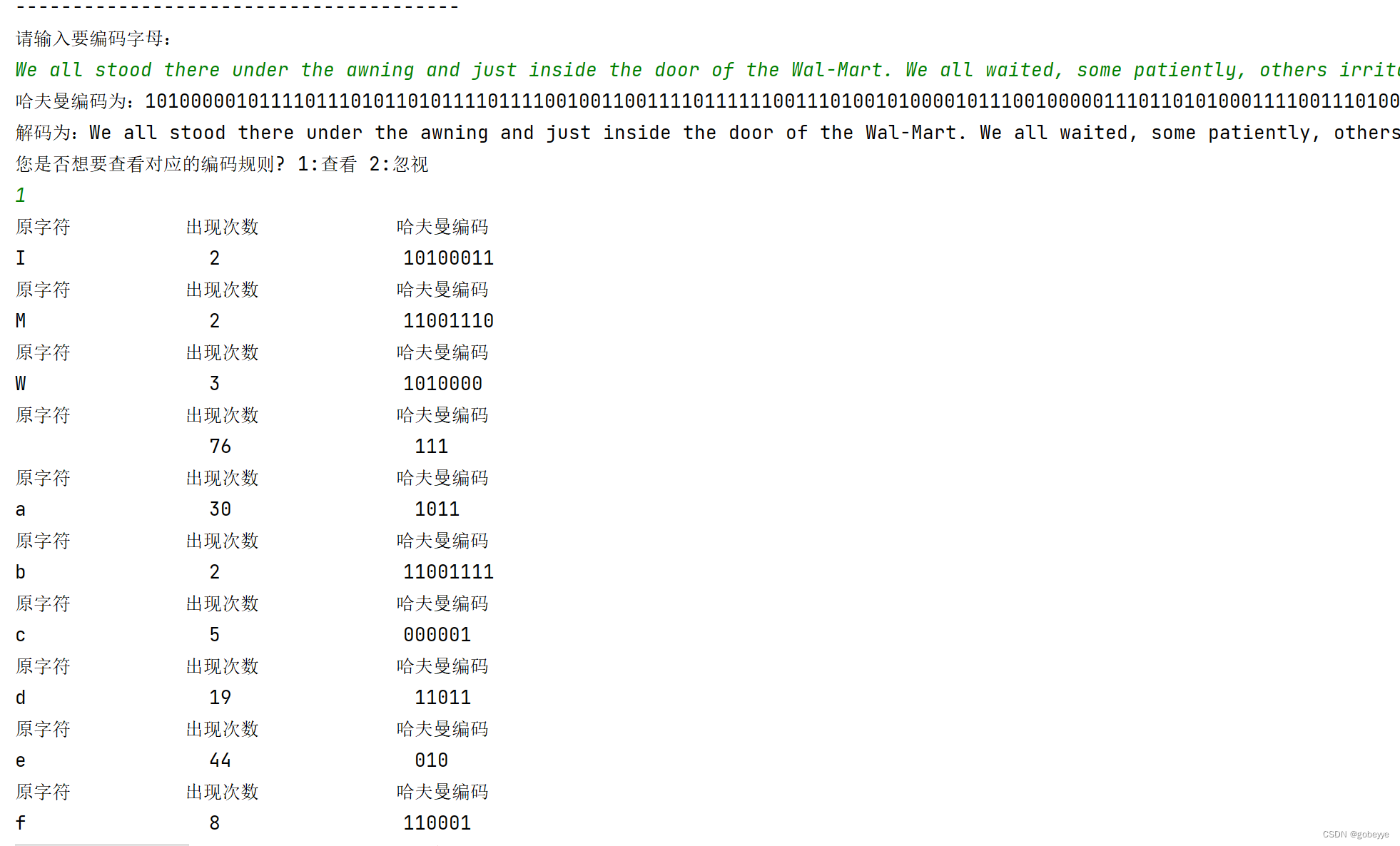
四、分析与探讨
哈夫曼编码分析和探讨:
高效压缩:通过为不同频率的字符分配不同长度的编码,能极大地减少表示文本所需的总位数,实现高效压缩。
自适应性:可以根据实际数据中字符的频率分布动态生成编码,适用于各种不同类型的数据。
最优性:在一定条件下,它能生成最优的无前缀编码,保证解码的唯一性和准确性。
例如,对于一个包含大量重复字符的文本,哈夫曼编码可以使这些高频字符的编码很短,从而节省大量存储空间。
总体而言,哈夫曼编码与解码是一种非常有效的数据压缩和恢复技术,在数据存储、传输等方面有着重要的应用价值。
总结:在参与这次团队合作实验的过程中,我获得了许多深刻的感悟和宝贵的经验。团队合作让我明白了集体力量的强大。当我们将每个人的智慧、技能和努力汇聚在一起时,能够解决许多单凭个人难以攻克的难题。不同成员的独特视角和想法相互碰撞、融合,为实验带来了更多的创新思路和解决方案。
有效的沟通在团队合作中至关重要。我们学会了清晰地表达自己的观点和想法,同时也认真倾听他人的意见。通过及时、准确的沟通,避免了误解和重复工作,确保整个团队始终朝着共同的目标前进。
分工与协作是团队高效运作的关键。根据成员的优势和特长进行合理的分工,让每个人都能在自己擅长的领域发挥最大作用。同时,在执行过程中,成员之间紧密协作,相互支持、配合,使得实验的各个环节能够顺利衔接。
面对实验中的困难和挑战,团队的凝聚力得以充分体现。大家共同面对问题,积极寻找解决办法,不推诿责任,这种团结一心的精神让我们能够战胜诸多困难。
这次团队合作实验也让我看到了自己的不足之处,比如在沟通技巧和团队协调方面还有待提升。这促使我在今后更加注重自身能力的培养和完善。
五、源码
源码在文章开头已经给出,这里就解释一下里面一些方法(createHT,createHCode),帮助理解一下。
5.1 createHT:
此方法的作用为构建哈夫曼树,有了哈夫曼树后才能进行哈夫曼编码。为了方便大家理解这里我用案例字符串:ABBBCCCCCDDDDDDD。来给大家手动模拟一下。首先统计出对应字母出现的次数。字母后面对应的数字就是对应的出现次数。

接着每次都从中挑选两个出现次数最小的进行合并。并合并后的节点权重为原来两个节点之和。
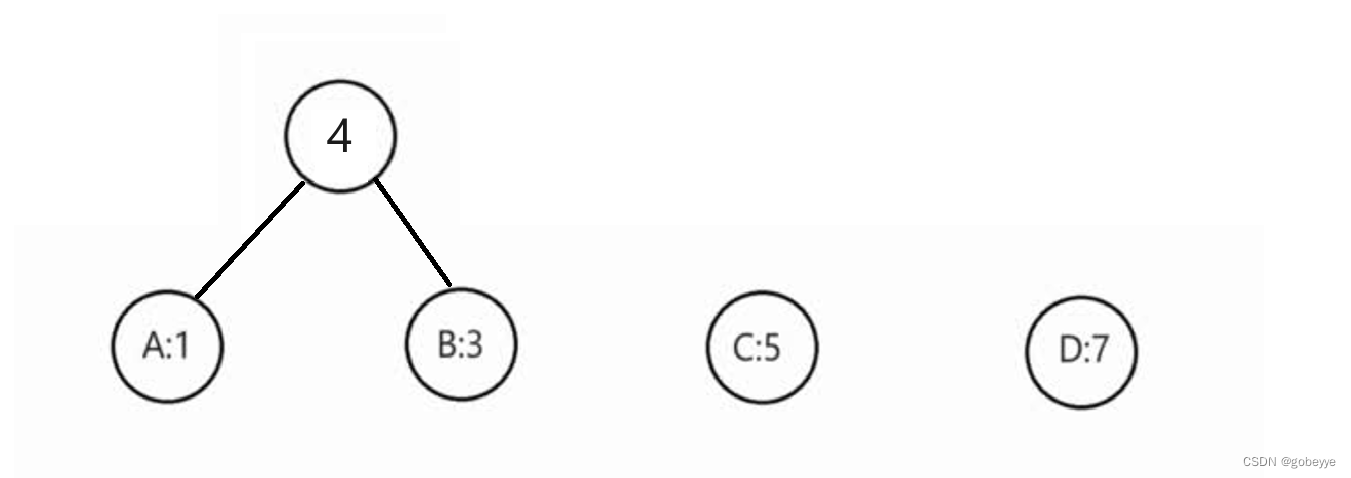
后续都一样,我就直接给出结果。注意:我们下面写的代码是左孩子是最小的,右孩子是次小的。
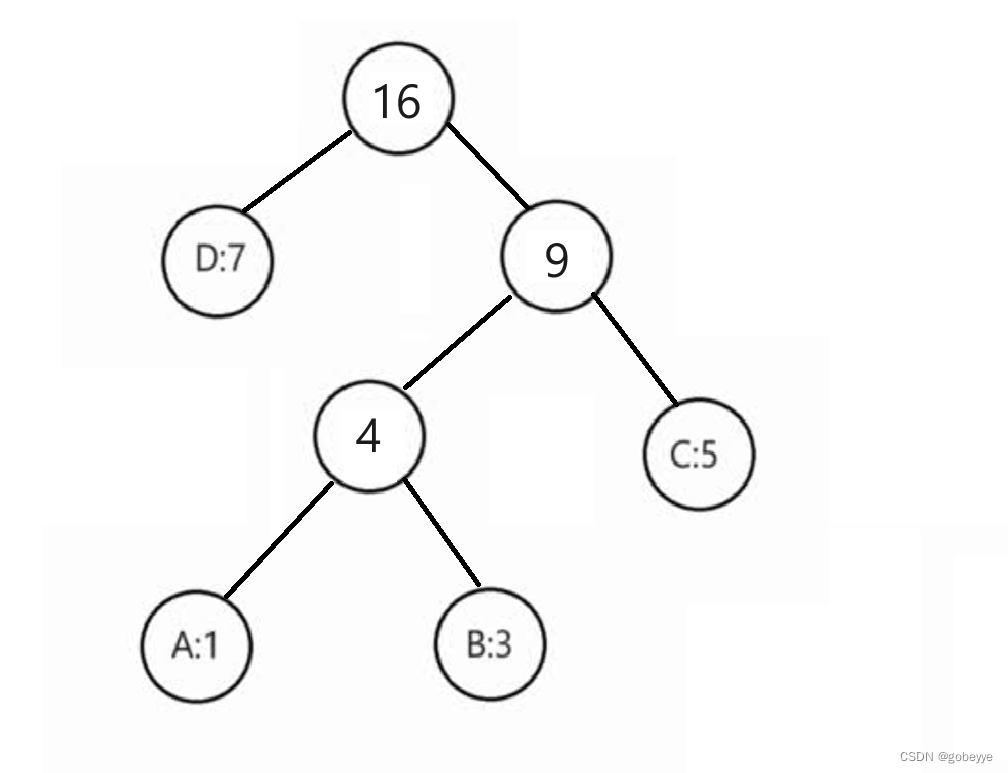
HTNode 的代码表示的是哈夫曼树的节点,参数有字符,权重,父亲,左右孩子节点参数。
- public class HTNode {
- char data;//字符
- int weight;//权重
- int parent;//父亲节点
- int lchild;//左孩子
- int rchild;//右孩子
- //对应的构造方法,初始化对应参数。
- public HTNode(char data,int weight){
- this.data = data;
- this.weight = weight;
- this.lchild = -1;//没有都初始化成 - 1
- this.rchild = -1;
- this.parent = -1;
- }
- //第二种构造方法,用来应对两种方式
- public HTNode(){
- this.lchild = -1;
- this.rchild = -1;
- this.parent = -1;
- }
- }

下面的代码就是模拟上面的这个过程,代码如下:
- //创建哈夫曼树
- //调试完毕
- //参数说明:ht 表示传入的叶子节点,n 表示叶子节点数
- //作用:构建哈夫曼树,存储在 ht 中。
- public static void createHT(HTNode ht[], int n) {
- //初始化
- int k = 0;//用来后续查找最小的两个叶子节点的权值下标
- int total = 2 * n - 1;//表示全部节点数
- double minl, minr;//存储区间内最小权值的两个节点
- int lnode, rnode;//存储最小权值的两个节点在数组中的下标
- for (int i = 0; i < total; i++) ht[i].parent = ht[i].lchild = ht[i].rchild = -1;//都初始化为 -1 ,表示叶子节点
- //开始创建
- for (int i = n; i < total; i++) {
- //要找最小,所以刚开始要初始化为 最大
- minl = 0x3f3f3f3f;
- minr = 0x3f3f3f3f;//minl 是最小的,minr 是次小的权值
- lnode = rnode = -1;//存储最小权值对应的下标
- for (k = 0; k <= i - 1; k++) {
- if (ht[k].parent == -1) {
- if (ht[k].weight < minl) //如果比 minl 还小的话,两个存储值都要改变
- {
- minr = minl;
- rnode = lnode;
- minl = ht[k].weight;
- lnode = k;
- } else if (ht[k].weight < minr) { //走到这里说明 minl 小于 ht[k].weight,所以只需要修改 minr 即可
- minr = ht[k].weight;
- rnode = k;
- }
- }
- }
- // i 表示 合并新节点的下标
- // lchild 表示被合并的左节点
- // rchild 表示被合并的右节点
- ht[i].weight = ht[lnode].weight + ht[rnode].weight;
- ht[i].lchild = lnode;
- ht[i].rchild = rnode;
- ht[lnode].parent = i;
- ht[rnode].parent = i;
- }
- }

5.2 createHCode:
案例字符串:ABBBCCCCCDDDDDDD。同样的我就直接利用上面构成的哈夫曼树来进行编码。
这个就更加简单,只需要记住左孩子是 0 ,右孩子是 1。
这里就直接给出编码的最终结果。
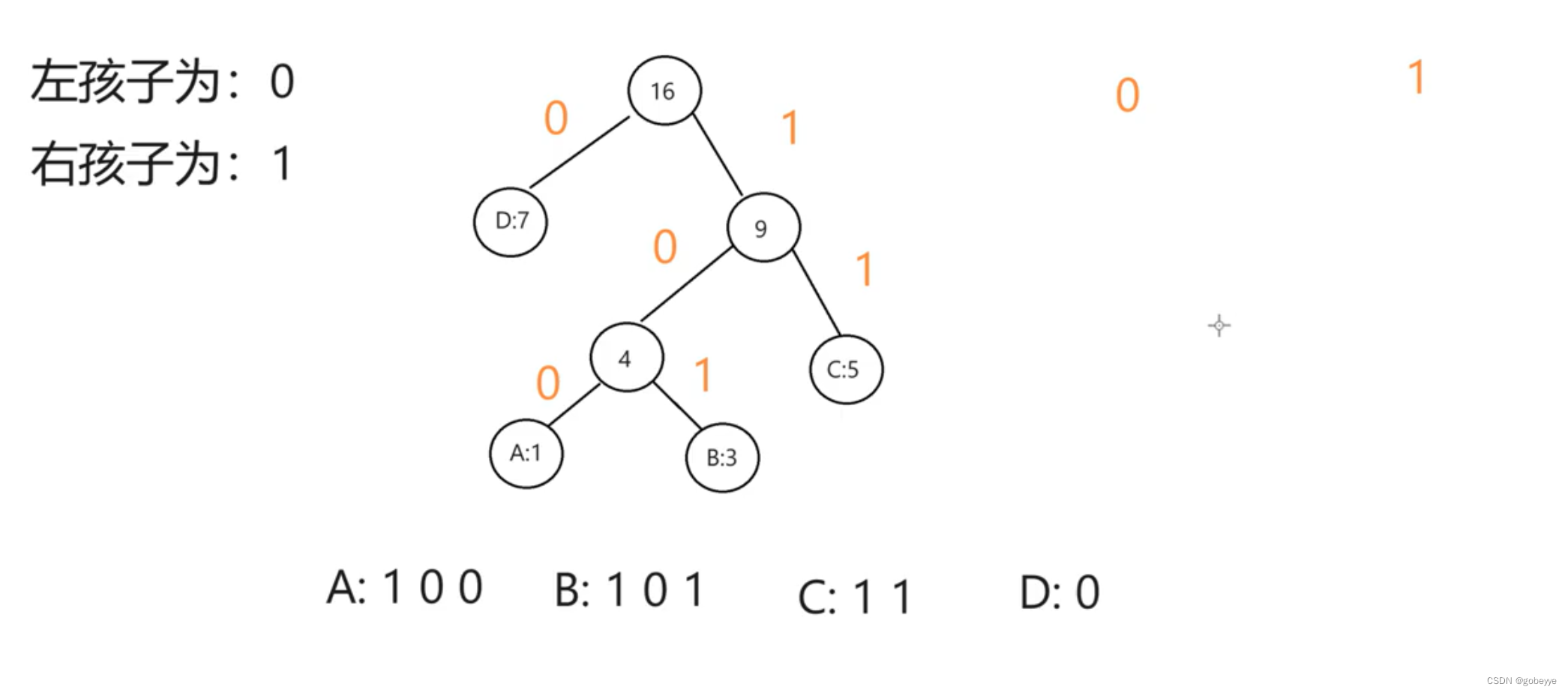
这是编码规则的节点设置,我们使用 StringBuilder 来存储最终的编码结果。(注意:看上图最后的叶子节点都是我们最初的节点。)使用 StringBuilder 的好处有不用频繁的创建对象,且有自带的字符串逆置方法(最后拿到的是逆序的,要将其转化一下)。
- public class HCode {
- StringBuilder cd;//哈夫曼编码
- char data;//存储字符,Java 的 char 是两个字节,所以能存储汉字
-
- /**
- * 构造方法,初始化 cd ,防止报错
- */
- public HCode(){
- cd = new StringBuilder();
- }
- }
对应的代码如下:
- /**
- * 方法作用为:创建哈夫曼编码规则
- * @param ht
- * @param n
- * @return
- */
- public static HCode[] createHCode(HTNode ht[], int n) {
- HCode[] hcds = new HCode[n];
- int parent; int cur;
- for (int i = 0; i < n; i++)
- {
- HCode tmp = new HCode();
- cur = i;
- //预备工作,初始化cur 和 parent
- parent = ht[cur].parent;
- tmp.data = ht[cur].data;
- while (parent != -1)
- {
- if (cur == ht[parent].lchild)
- {
- //是左孩子
- tmp.cd.append('0') ;
- }
- else
- {
- //右孩子
- tmp.cd.append('1') ;
- }
- //向上查找
- cur = parent;
- parent = ht[cur].parent;
- }
- //进行翻转
- tmp.cd = tmp.cd.reverse();
- hcds[i] = tmp;
- }
- return hcds;
- }

到这里大部分代码逻辑就讲述完毕,剩下的一些零碎,在源码里面都有解释,请放心食用
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。


