【Java--数据结构】二叉树oj题（上）

前言

欢迎关注个人主页：逸狼

---

创造不易，可以点点赞吗~

如有错误，欢迎指出~

---

---

判断是否是相同的树

oj链接

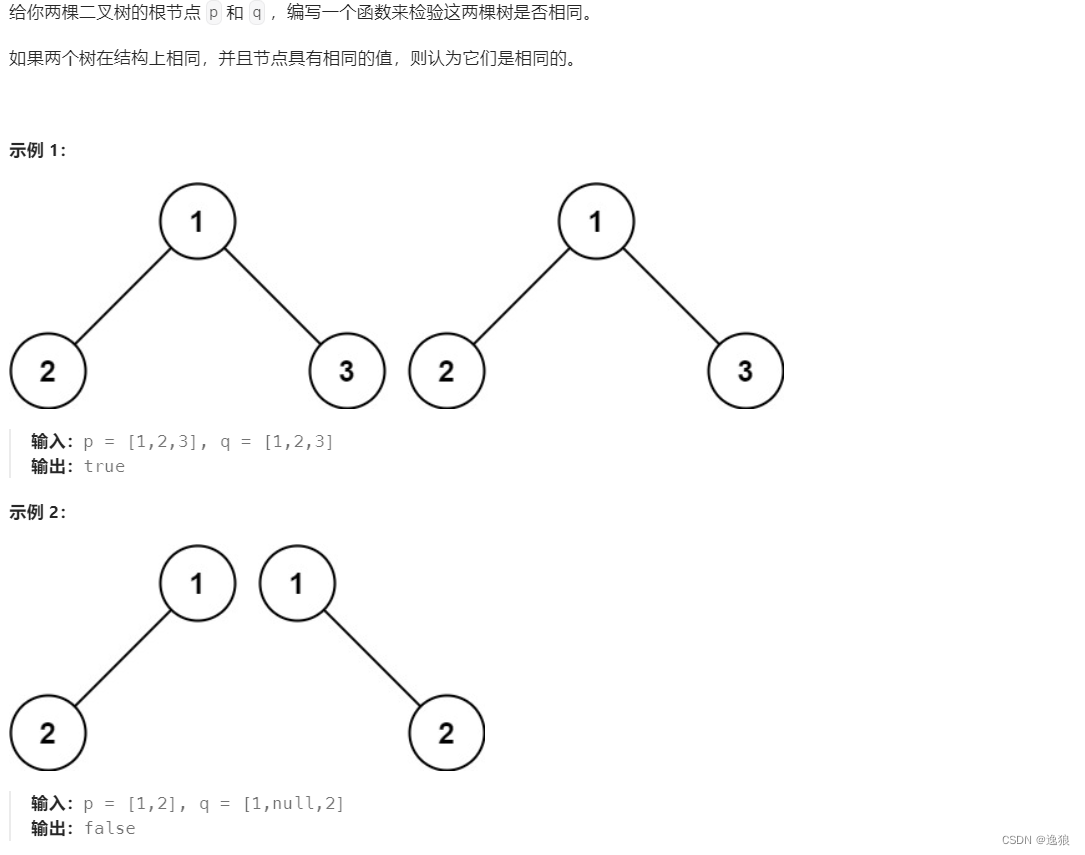
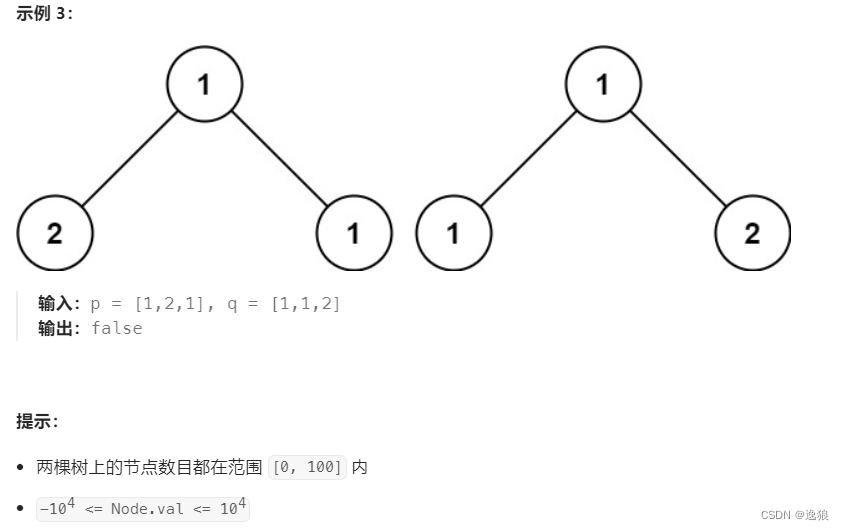
要判断树是否一样，要满足3个条件

• 根的 结构 和 值 一样
• 左子树的结构和值一样
• 右子树的结构和值一样

所以就可以总结以下思路：

1. 一个为空，一个不为空--》一定不相同
2. 两个都为空--》                  相同
3. 都不为空 ，但值不一样--》一定不相同
4. 最后递归判断 左子树和右子树都要相同--》两棵树相同

其中该题的时间复杂度为O（min(m,n)）,也就是取m和n中最小值（假设p的节点数为m个，q的节点数为n个）

public boolean isSameTree(TreeNode p, TreeNode q) {
        //一个为空，一个不为空
        if(p!=null&&q==null||p==null&&q!=null){
            return false;
        }
        //此时要么两个都为空，要么都不为空
        if(p==null&&q==null){
            return true;
        }
        //都不为空
        if(p.val!=q.val){
            return false;
        }
        //此时两个都不为空，val值也一样，说明根节点相同
        //判断左右树是否相同
        return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);

另一棵树的子树

oj链接

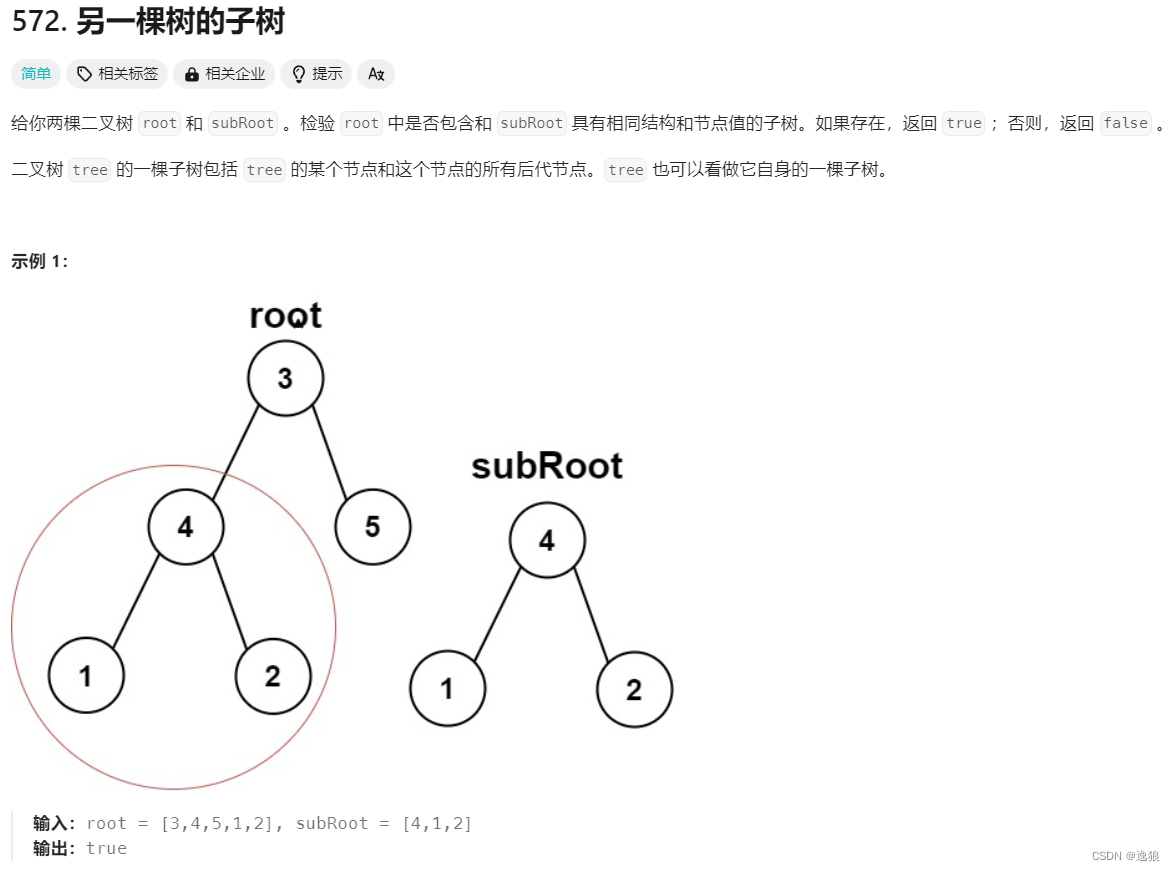
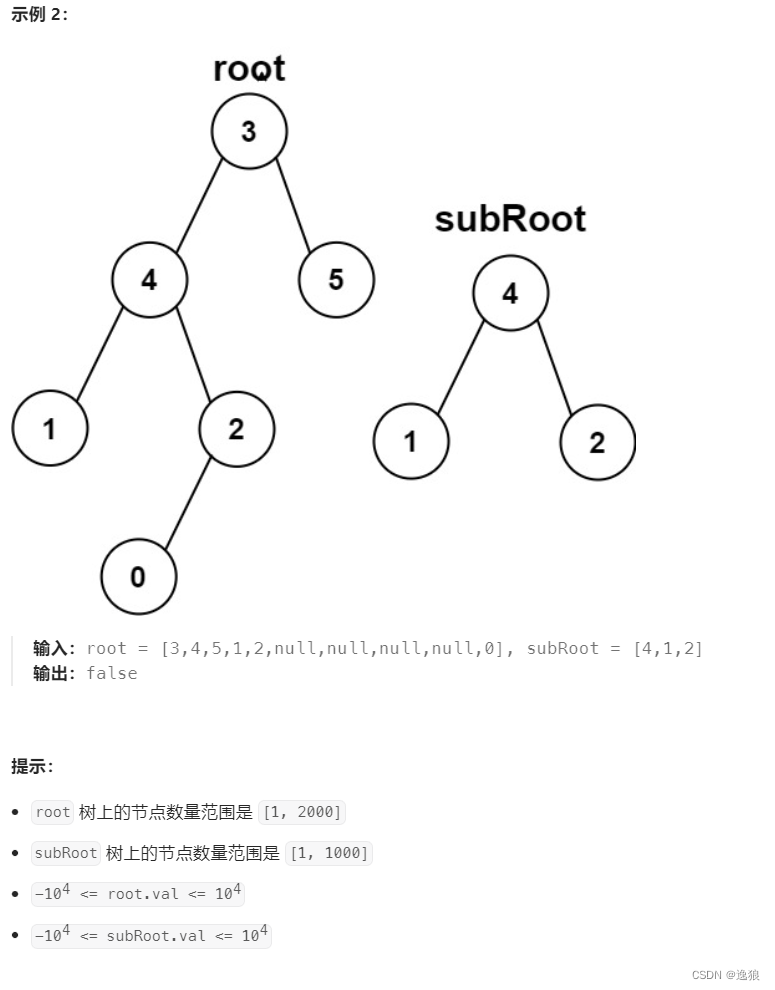
当两颗树相同时，也属于子树

所以步骤如下

1. 判断是不是两颗相同的树
2. 若不是，有可能是左子树的子树
3. 也有可能是右子树的子树

其中该题的时间复杂度为m*n  （假设root有n个节点，subRoot有m个节点），原因是root的每一个节点都要和subRoot的节点比对

    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        //因为root要递归，递归到后面root可能为空
        if(root==null){
            return false;
        }
        //两颗树相同时，成立
        if(isSameTree(root,subRoot)){
            return true;
        }
        //判断root的左子树和subRoot
        if(isSubtree(root.left,subRoot)){
            return true;
        }
        //判断root的右子树和subRoot
        if(isSubtree(root.right,subRoot)){
            return true;
        }
        return false;
 
    }
 
        public boolean isSameTree(TreeNode p, TreeNode q) {
        //一个为空，一个不为空
        if(p!=null&&q==null||p==null&&q!=null){
            return false;
        }
        //此时要么两个都为空，要么都不为空
        if(p==null&&q==null){
            return true;
        }
        //都不为空
        if(p.val!=q.val){
            return false;
        }
        //此时两个都不为空，val值也一样，说明根节点相同
        //判断左右树是否相同
        return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
 
    }

翻转二叉树

oj链接

让root的左节点和右节点交换，再递归遍历root.left和root.right使左子树和右子树都翻转。

代码优化：若只有一个根节点（左右子树都为空），直接返回；减少了递归和交换的次数

    public TreeNode invertTree(TreeNode root) {
        if(root==null){
            return null;
        }
        //代码优化部分******减少一些递归和交换的次数
        if(root.left==null&&root.right==null){
            return root;
        }
        //          ******
        TreeNode ret=root.left;
        root.left=root.right;
        root.right=ret;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }

判断一颗二叉树是否是平衡二叉树

平衡二叉树 是指该树所有节点的左右子树的深度相差不超过 1

oj链接

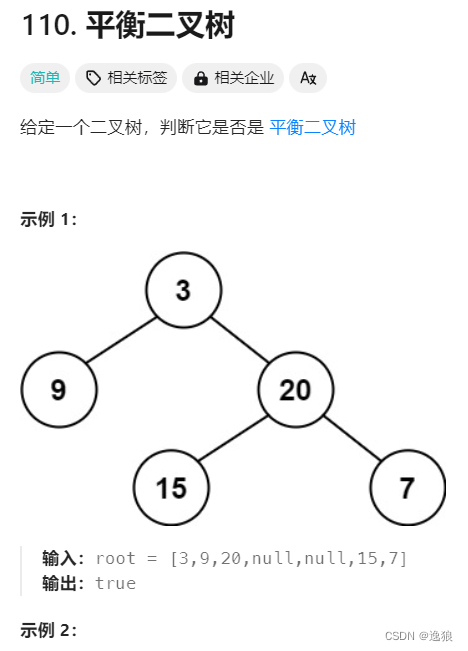
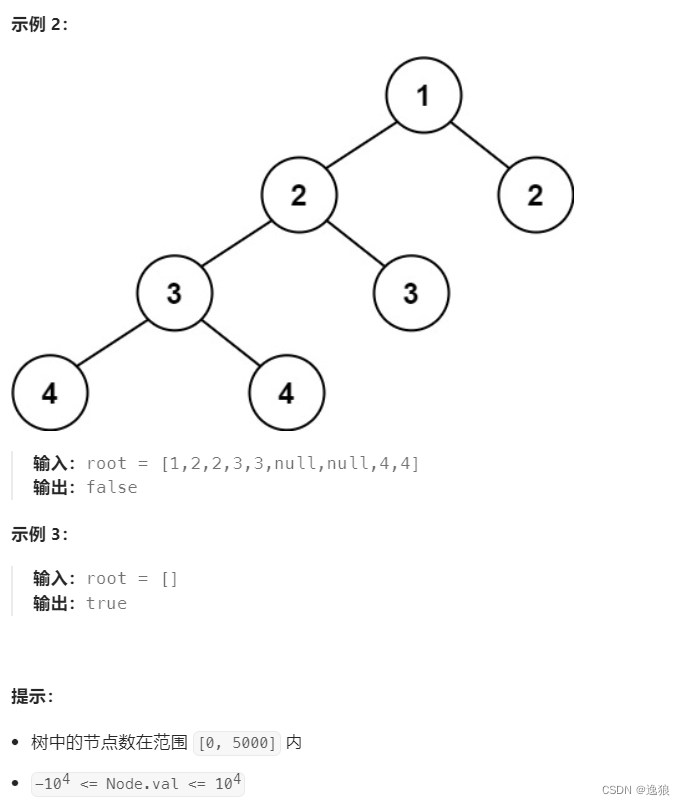
 判断步骤：

当前root的 左子树 和 右子树的高度差<=1

同时满足root的左 右子树平衡

 其中该题的时间复杂度为O（n^2）

    public boolean isBalanced(TreeNode root) {
        if(root==null) return true;
        int leftH=maxDepth(root.left);
        int rightH=maxDepth(root.right);
 
        return Math.abs(leftH-rightH)<=1
        &&isBalanced(root.left)
        &&isBalanced(root.right);
    }
    public int maxDepth(TreeNode root){
        if(root==null){
            return 0;
        }
        int leftH=maxDepth(root.left);
        int rightH=maxDepth(root.right);
        return leftH>rightH?leftH+1:rightH+1;
    }

 代码优化，使得时间复杂度变为O（n）

    public boolean isBalanced(TreeNode root) {
        if(root==null) return true;
        return maxDepth(root)>=1;
    }
    public int maxDepth(TreeNode root){
        if(root==null){
            return 0;
        }
        int leftH=maxDepth(root.left);
        if(leftH<0){
            return -1;
        }
        int rightH=maxDepth(root.right);
        if(rightH<0){
            return -1;
        }
        if(Math.abs(leftH-rightH)<=1){
            return leftH>rightH?leftH+1:rightH+1;
        }else{
            return -1;
        }
 
    }

第三种写法

    public boolean isBalanced(TreeNode root) {
        if(root==null) return true;
        return maxDepth(root)>=1;
    }
    public int maxDepth(TreeNode root){
        if(root==null){
            return 0;
        }
        int leftH=maxDepth(root.left);
        // if(leftH<0){
        //     return -1; 
        // }
        int rightH=maxDepth(root.right);
        // if(rightH<0){
        //     return -1;
        // }
        if(leftH>=0&&rightH>=0
        &&Math.abs(leftH-rightH)<=1){
            return Math.max(leftH,rightH)+ 1;
        }else{
            return -1;
        }
    }