八大排序时间复杂度与稳定性_各种排序方法的时间复杂度与稳定性

目录

一、冒泡排序

时间复杂度：

稳定性

二、快速排序

时间复杂度：

稳定性

三、直接插入排序 

时间复杂度：

稳定性

四、希尔排序

时间复杂度：

稳定性

五、选择排序 

时间复杂度：

稳定性 

六、堆排序

时间复杂度：

稳定性

七、归并排序

时间复杂度：

稳定性

八、计数排序 

时间复杂度：

​编辑稳定性

斗蛐蛐代码

---

一图览：

         

---

一、冒泡排序

时间复杂度：

最好：O(n)，当数组有序时，遍历一遍就是完成排序（只有优化情况下才有最好）

最坏：O(n^2)

平均时间复杂度：O(n^2)

        

空间复杂度：

O(1)

一共要走n-1趟：

每一趟能排好一个数据，一共n个数据，如果前n-1个都排好了，那么最后一个就不用排了

每一趟要比较 n -i -1次：

对于n个数据，前后按顺序比较一共要比较n-1次。因为每排好一个数据，每一趟就可以少比较一次，因为前面的数据肯定比排好的数据大/小。

void BubbleSort(int* a, int n)
{
	for (int i = 0; i < n-1; i++)//一共走n-1趟
	{
		int flag = 0;//优化代码而设置的变量
		for (int j = 0; j < n - i-1; j++)//每趟比较n-i-1次
		{
			if (a[j] > a[j + 1])
			{
				swap(&a[j], &a[j + 1]);
				flag = 1;//若发生了交换，则flag置1
			}
		}
		if (flag == 0)//若flag==0，代表这一趟没有任何数据发生交换，说明前后数据严格遵守升/降序，所以数组有序
			break;
	}
}

稳定性

稳定

虽然我慢，但是我很稳定啊！！

由于每次比较都是两个数之间的比较，满足条件就交换，不满足就什么也不做。所以他和其他数据的相对位置不会发生任何改变

         

---

二、快速排序

时间复杂度：

最好：O(n*log n)

最坏：O(n^2)（一般情况下很少出现，所以我们不用最坏情况为其时间复杂度）

平均时间复杂度：O(n*log n)

        

空间复杂度：

O(log n)

任何快排的实现方法的时间复杂度都相同

一共走 log n 趟：

用二分法，类比二叉树。每次确定好一个数据的位置，然后把这个数据分为左右两部分，大多分 log n 次就可以把数组分到不能再分。

每一趟走 n 次：

因为每一趟排好一个数据后，会把这个数组一分为二，而被分成的这两个数组总元素少1（可忽略，因为到最后这个总元素不会相差原始元素个数太多，若差10则说明有1024个数据）。所以可以把每一趟要走的次数认为是 n 次

最坏情况

数组有序，则要走 n 趟，每趟走 n-i-1 次。也就是 n-1 + n-2 + n-3 ..... + 1 

最后得出的数量级就是 n^2

稳定性

不稳定

虽然我很快，但代价就是不稳重

        

---

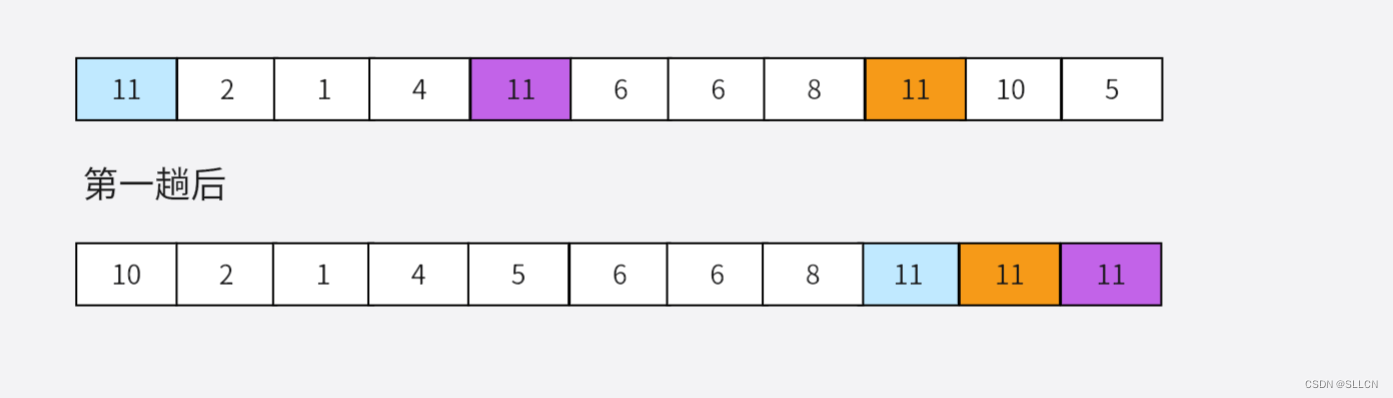
三、直接插入排序 

时间复杂度：

最好：O(n)，数组有序，遍历每个数据都不用往前找，直接插入

最坏：O(n^2)，数组全逆序，每个数据都要向前挨个找，找到第一个再插入

平均时间复杂度：O(n^2)

        

空间复杂度：

O(1)

 

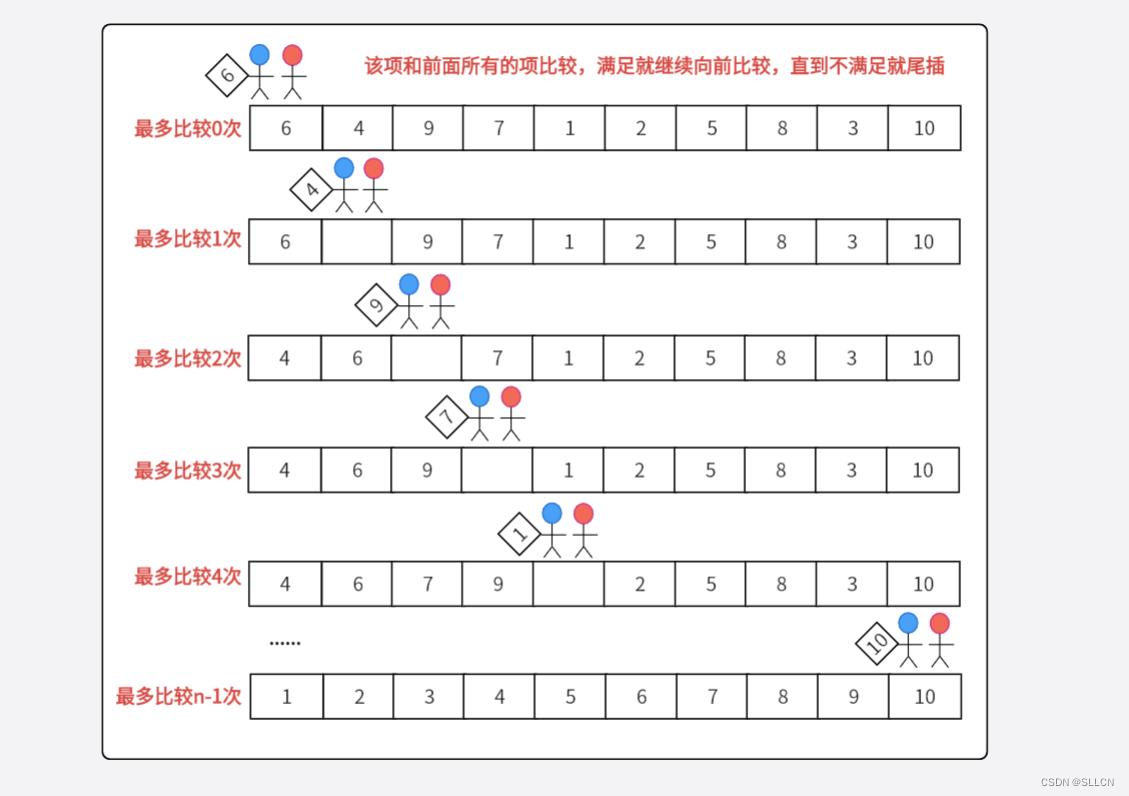
一共走 n 趟：（n-1也可以，看看要不要把第一位也放进去）

要把每个数据都进行一次插入操作，所以要走 n 趟

每一趟最多走 n-i-1 次：

每一趟的这一个待插入数据，都要向前挨个找，找到满足的为止，最多走 n-i-1 次，最少直接插入

稳定性

稳定（一般来说是稳定的）

看具体实现，如果代码是两数相等的时候不再往前找，那么就是稳定的

        

---

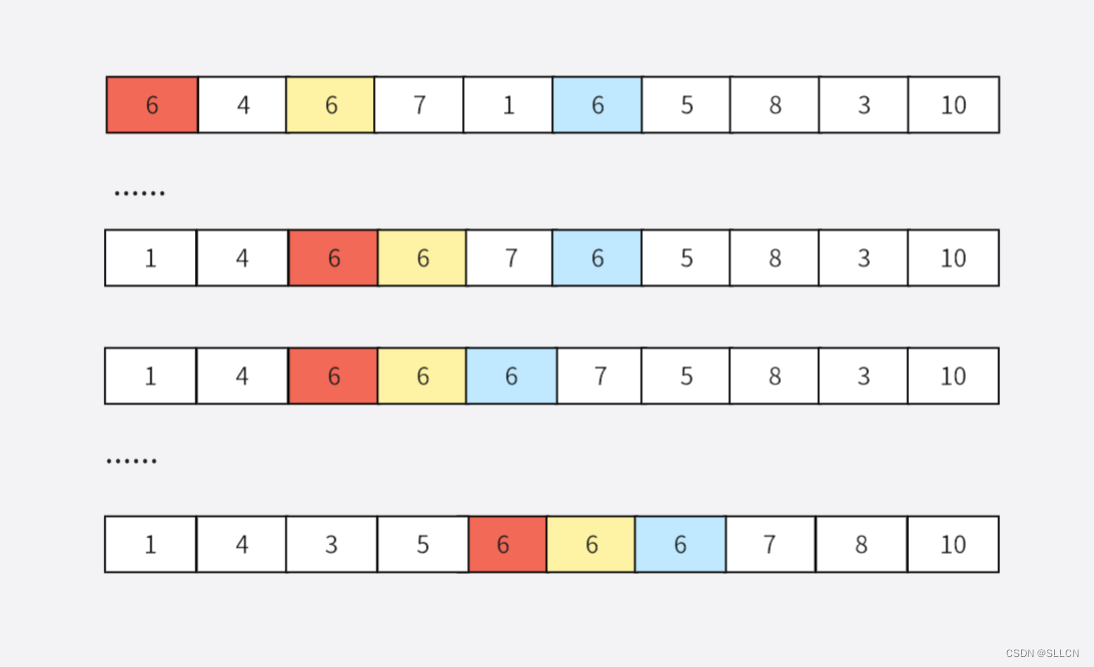
四、希尔排序

时间复杂度：

最好：O(n*log^2 n)

最坏：O(n*log^2 n)

平均时间复杂度：O(n*log n)

        

空间复杂度：

O(1)

 希尔的时间复杂度十分难计算，这里给个大概的计算方式，用的时候默认记住O(n*log n)就行

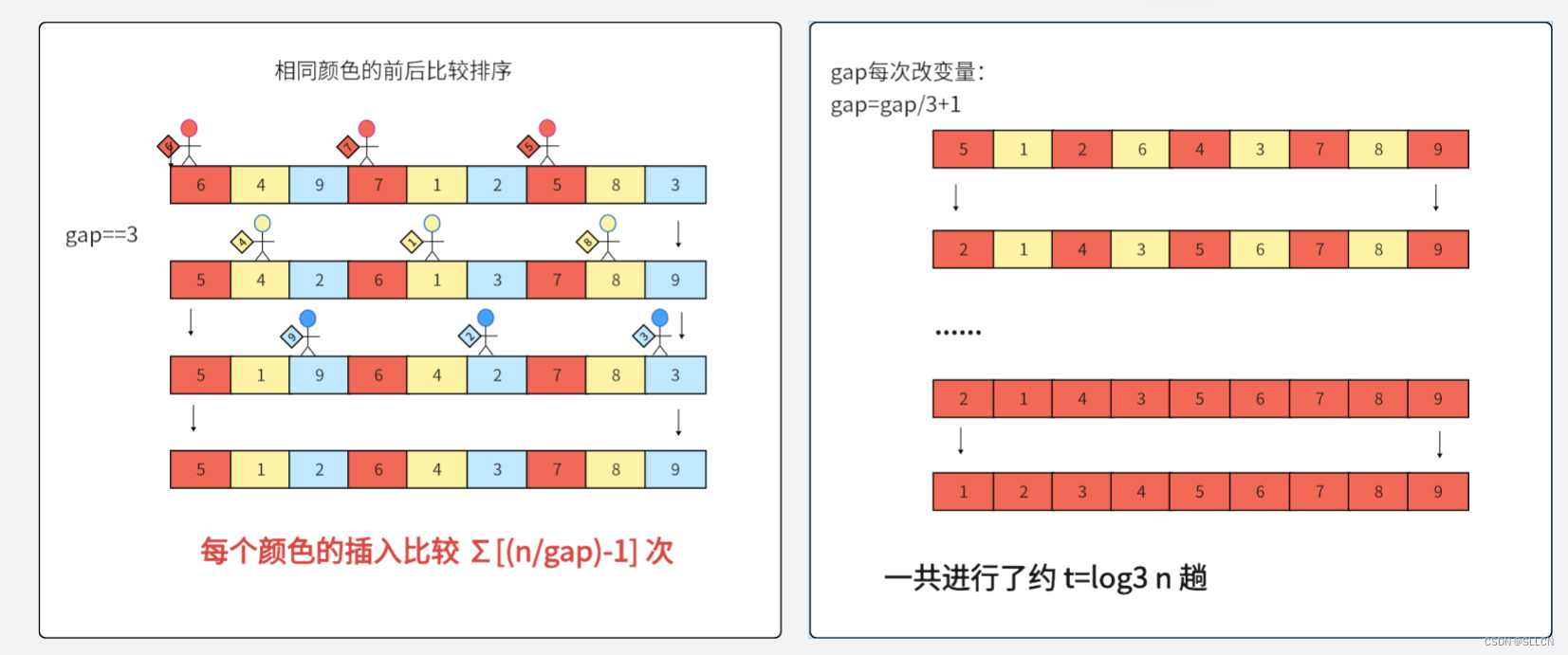
一共走约 log3 n 趟：

如果gap每次÷3的话，那么一共会除约 log3 n 次

每一趟比较 gap*∑[(n/gap)-1] 次：

每一种颜色有约 (n/gap) 个（有个数差别是因为可能有些颜色最后会比别的颜色少/多1个）。每种颜色会进行 ∑[(n/gap)-1] 次比较（这里的比较实际上是类似于直接插入，只不过选数据的时候间隔不是1，而是gap）。一共有gap种颜色，所以是 gap*∑[(n/gap)-1] 次。

        

经过专业人士的计算，时间复杂度是O(n*log n)。

反正用的时候会发现，希尔是真

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小蓝xlanll/article/detail/164021