【Python】递归函数理解与练习_用python输入参数为n,返回1×2×3×...×(n-1)×n的值。

递归

在一个函数内部调用自身本身，就是递归函数。

阶乘

5 的阶乘为：5*4*3*2*1

n 的阶乘为：1*2*3*…*(n-1)

所以其实就是n * (n-1)的循环，只有当n=1时，需要特殊处理。

# 递归实现，暂不考虑负数和零
def fact(n):
    if n == 1:
        return 1
    return n * (fact(n-1))

>>> fact(5)
120
1
2
3
4
5
6
7
8

当计算fact(5)时，函数运算过程如下：

>>> fact(5)
===> 5 * fact(4)
===> 5 * (4 * fact(3))
===> 5 * (4 * (3 * fact(2)))
===> 5 * (4 * (3 * (2 * fact(1))))
===> 5 * (4 * (3 * (2 * 1)))
===> 5 * (4 * (3 * 2))
===> 5 * (4 * 6)
===> 5 * 24
===> 120
1
2
3
4
5
6
7
8
9
10

递归函数的优点是定义简单，逻辑清晰。理论上，所有的递归函数都可以写成循环的方式，但循环的逻辑不如递归清晰。

使用递归函数需要注意防止栈溢出。在计算机中，函数调用是通过栈（stack）这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，会导致栈溢出。

Python 3.7 的最大递归深度为 998，如果超出就会报错，比如：

>>> fact(999)
Traceback (most recent call last):
File "test.py", line 28, in fact
    if n == 1:
RecursionError: maximum recursion depth exceeded in comparison
1
2
3
4
5

当然这个递归深度可以修改，998 只是一个默认值

import sys
sys.setrecursionlimit(1000)  # 设置最大递归深度 1000

# 源码解释 sys.py
def setrecursionlimit(n): # real signature unknown; restored from __doc__
    """
    setrecursionlimit(n)
    
    Set the maximum depth of the Python interpreter stack to n.  This
    limit prevents infinite recursion from causing an overflow of the C
    stack and crashing Python.  The highest possible limit is platform-
    dependent.
    """
    pass
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

练习

汉诺塔（http://www.hannuota.cn）

游戏介绍
源于印度一个古老传说的益智玩具，大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着 64 片黄金圆盘，并且预言当僧侣将 64 片圆盘从 A 柱移动到 C 柱时，时间就会在一声霹雳中毁灭。

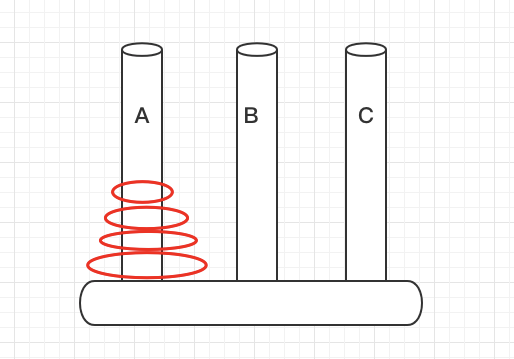
游戏规则

• 全部圆环从 A 柱移动到 C 柱视为完成
• 每次只能移动一个圆环，必须在三个柱子间移动
• 在小圆环上不能放大圆环，小圆环在上 大圆环在下

游戏原理
当看到这个游戏规则时，可能会产生疑惑，这个跟递归有什么关系呢？先别着急，慢慢往下分析。

当圆环数为 1 时，完成步骤：

A --> C

非常简单，直接把圆环从 A 放到 C 就可以完成。

增加难度，当圆环数为 2 时，完成步骤：

A --> B
A --> C

为方便描述，P 代表圆盘，P2 > P1

当我们想把第 P2 移动到 C 柱时，由于每次只能移动一个圆环，所以先要把 P1 移动到 B 柱上，P2 才可以移动到 C 柱。

继续增加难度，当圆环数为 3 时，目标是 P3 移动到 C 柱，反推一下：只有当 P3 上面没有其他圆盘时，才可以移动，所以 P2 和 P1 需要移动到 B 柱。

• P1 移动到 C 柱（保证 P2 可以移动，先移开）
• P2 移动到 B 柱
• P1 再次移动到 B（C 柱就空出来了）
• P3 移动到 C 柱（变成了 P2 移动到 C 柱的问题）
• P1 移动到 A 柱（变成了 P1 移动到 C 柱的问题）
• P2 移动到 C 柱

完成步骤如下：

A --> C
A --> B
C --> B
A --> C
B --> A
B --> C
A --> C

图示：

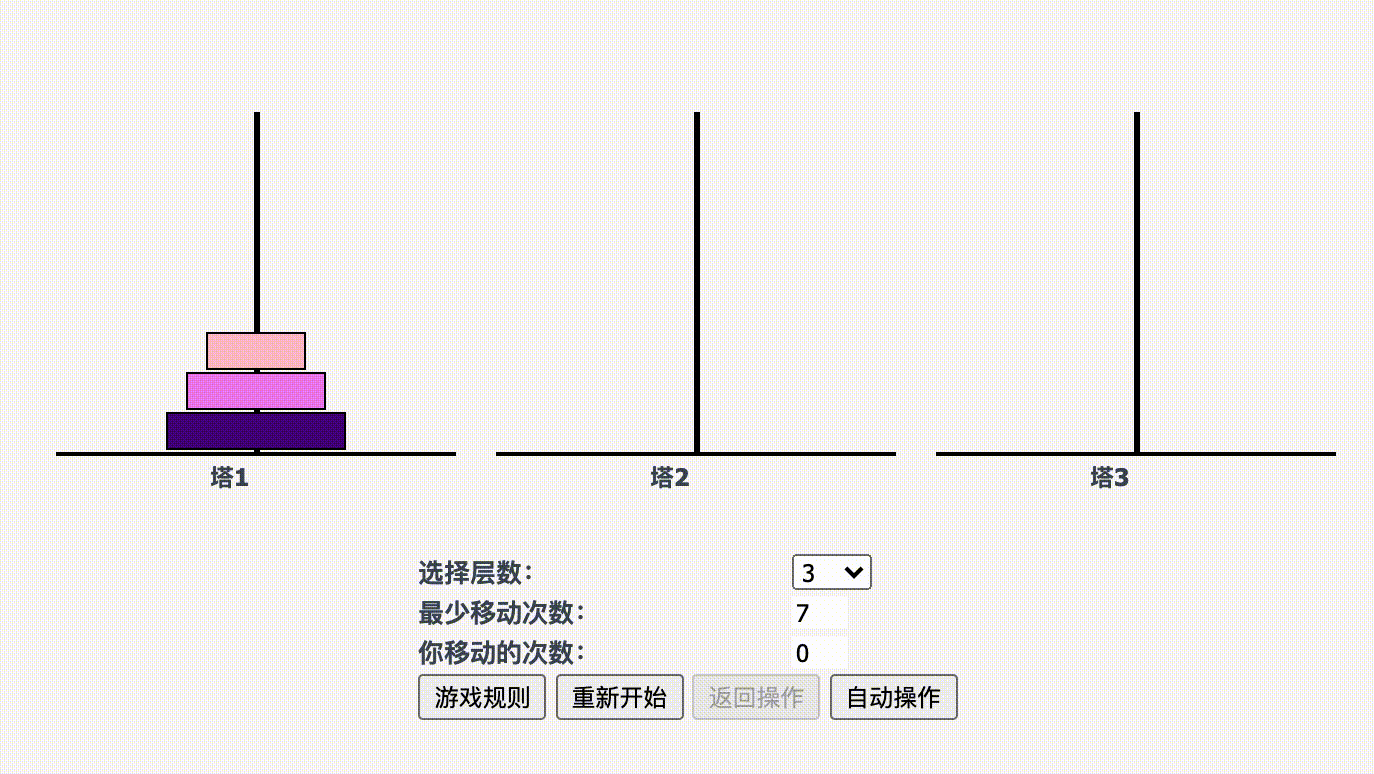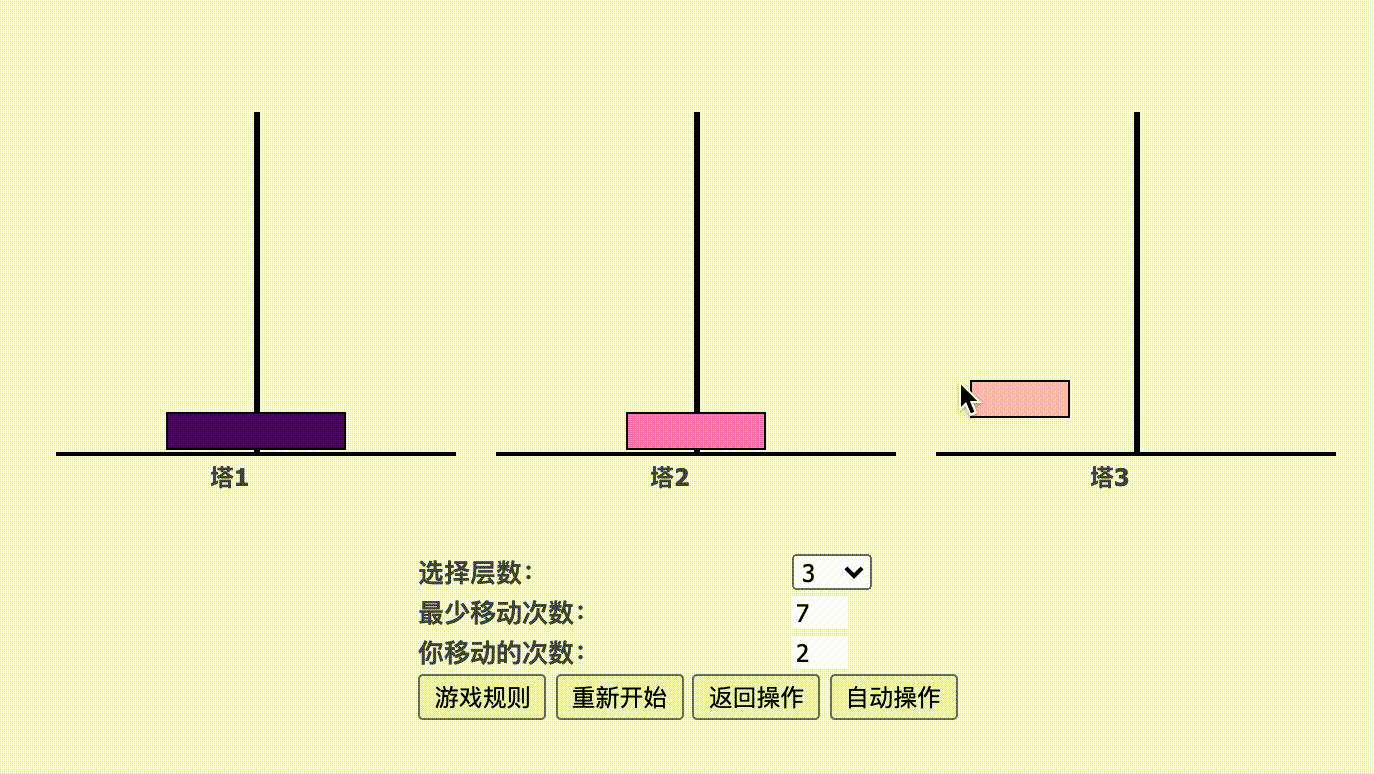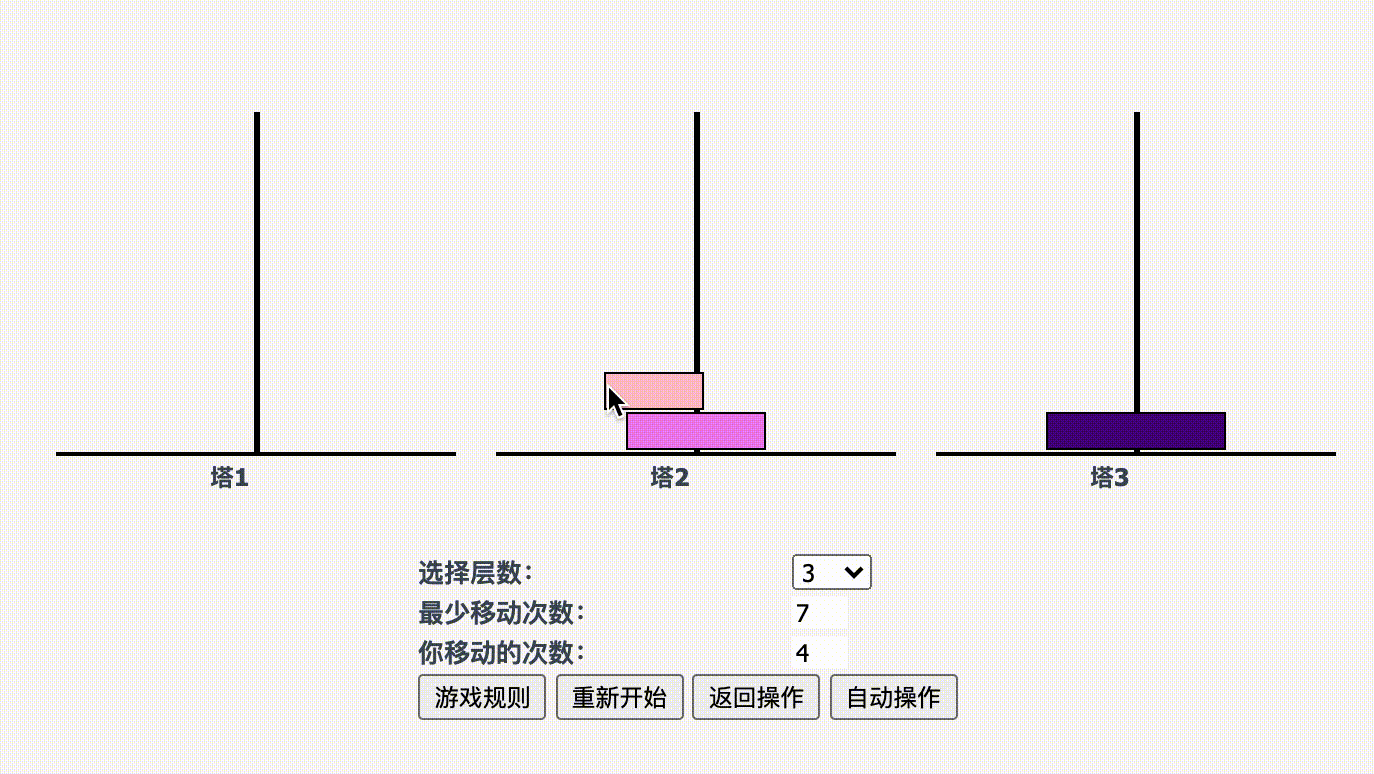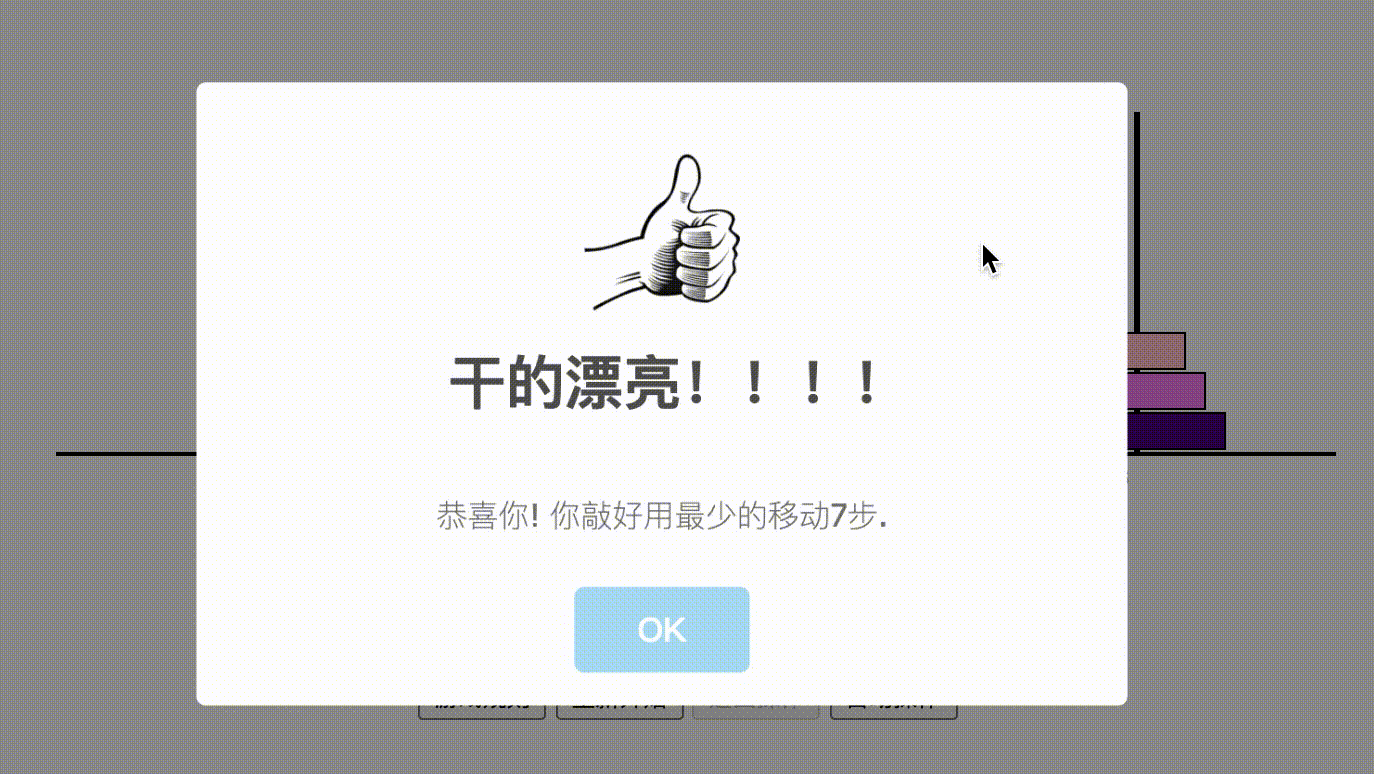
再次梳理一下 3 个圆盘的移动规则，为满足将全部圆盘移动到 C 柱：

1. 前两个圆盘移动到 B 柱；
2. 第三个圆盘移动到 C 柱；
3. 两个圆盘移到 C 柱；

所以如果为 n 个圆盘的话，那么：

1. n-1 个圆盘移动到 B 柱；
2. n 移动到 C 柱；
3. n-1 个圆盘从 B 柱移动到 C 柱子

所以，这是一个递归的问题，代码实现

def hanoi(n, a, b, c):
    if n == 1:
        print(f"{a} --> {c}")
        return
    hanoi(n-1, a, c, b)
    hanoi(1, a, b, c)
    hanoi(n-1, b, a, c)

>>> hanoi(3, "A", "B", "C")
1
2
3
4
5
6
7
8
9

题外话

梵天说当僧侣完成 64 层汉诺塔时，世界就会毁灭，那么完成它需要多长时间呢？

根据上面的规律可得：

f(n) = f(n-1) + 1 + f(n-1)
f(n) = 2f(n-1) + 1

移动 1 个圆盘：
f(1) = 1 = $2^1-1$

移动 2 个圆盘：
f(2) = 3 = $2^2-1$

移动 3 个圆盘：
f(3) = 7 = $2^3-1$
…
f(64) = $2^{64}-1$

>>> (2**64 - 1) / (60*60*24*365)
584942417355.072
1
2

得出结果 5800 亿年，宇宙形成到现在经过了 138 亿年，所以这么久远的未来是想象不到的… 不过人家梵天的数字底子是真不赖。

---

结束

递归学习是跟随廖雪峰老师的教程走的，后续理解是看 B 站李永乐老师的讲解明白的，感谢。我的文字水平有限，如果表述不清楚，就看下方视频 + 多玩游戏，肯定能弄明白。

视频地址：
https://www.bilibili.com/video/BV1gJ41177fX?from=search&seid=4494680542532501641
游戏地址：
http://www.hannuota.cn
教程：https://www.liaoxuefeng.com/wiki/1016959663602400/1017268131039072

当理解原理之后，玩汉诺塔很自然的就用最少步骤完成，知识就是力量，感谢阅读。