2D-3D配准指南[方法汇总]【入门指导向】（二）2D-3D MatchNet +pointnet_2d3d配准 评估

背景

近年来，采用三维和二维数据的应用层出不穷，它们都需要将三维模型与二维图像进行匹配。大型定位识别系统可以估算出照片拍摄的位置。在全球定位系统可能失灵的情况下，地理定位系统可以进行地点识别，对自动驾驶非常有用。此外，法医警察也可以利用该系统破案或防止袭击。
本文的目标是总结利用深度学习方法将二维图像到三维点云进行配准的方法。
整个文章系列将介绍LCD、2D-3D MatchNet、三元损失函数、VGG-Net、图神经网络等内容。

3. 2D-3D MatchNet: PointNet + VGG16 Triplet Loss Architecture

Mengdan Feng, Sixing Hu, Marcelo Ang, and Gim Hee Lee. 2d3d-matchnet: Learning to
match keypoints across 2d image and 3d point cloud, 2019.

2D-3D MatchNet提出了一种三支结构的三元组样式配置架构：通过修改的VGG16构建的用于处理图像patch的一支，以及两个使用共享权重的孪生PointNet架构，用于处理点云patch。这样的模型能够将从图像和点云数据中提取的特征编码为落在相同空间内的embedding。

2.2.1 网络架构

以下是论文中提出的网络架构：

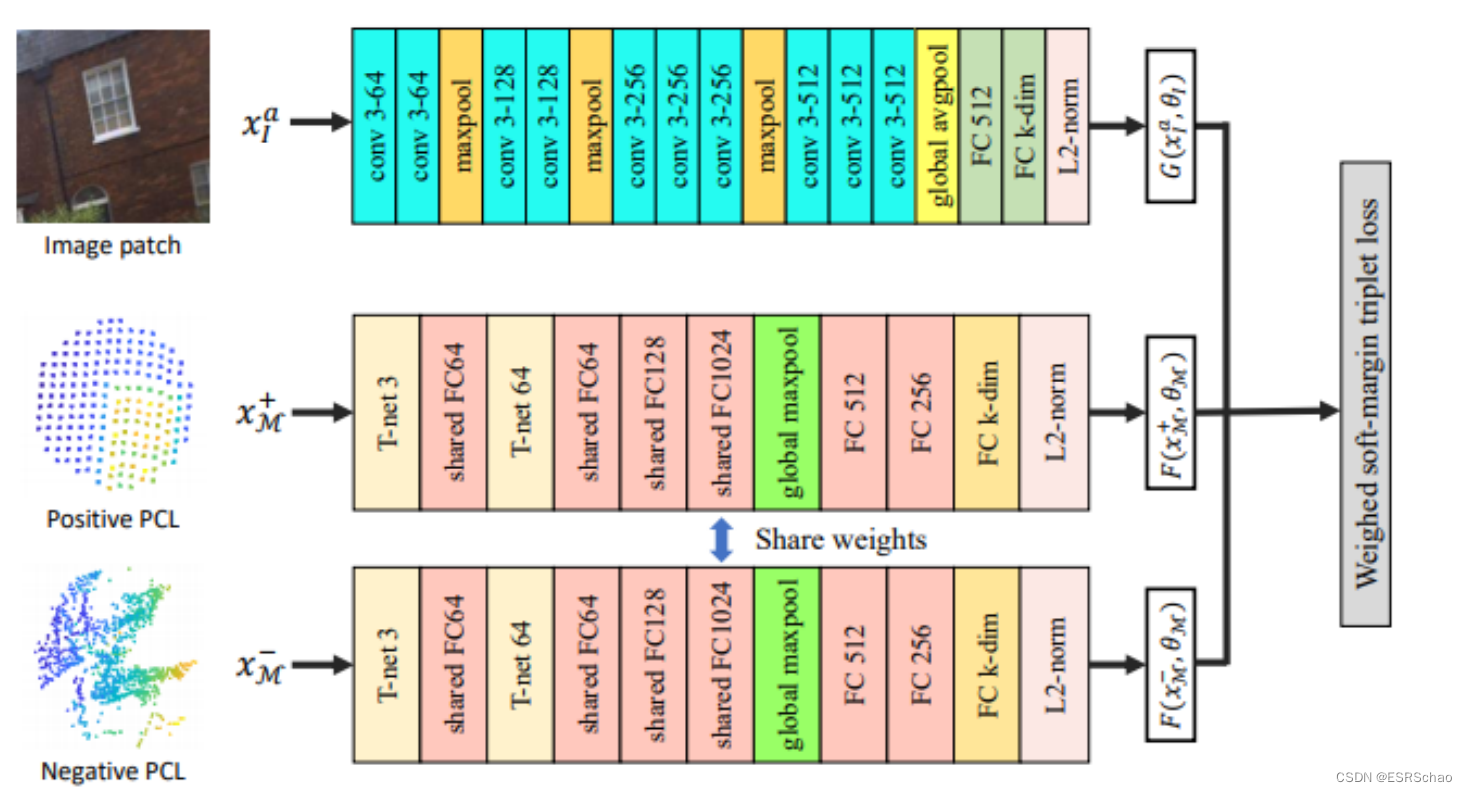
如图所示，所提出的网络由三个分支组成。一个学习输入图像patch的描述符，而另外两个基于输入的点云生成embedding。
在训练期间，图像patch和点云patch以图像锚点、其匹配点云和随机选择的非匹配点云的形式馈送到网络中： { x a I , x M + , x M − } \{x_a^I, x^+_M, x^-_M\} {xaI​,xM+​,xM−​}。网络的任务是学习 $G(x_I;{\theta }_I):x_I\to p$ 和 $F(x_M;{\theta }_M):x_M\to a$，它们分别将输入图像patch $x_I$ 映射到其embedding $p$，以及输入点云 $x_M$ 映射到其embedding $q$。
为了实现 $G(x_I;{\theta }_I)$，网络使用了带有批标准化的VGG16架构。另一方面，$F(x_M;{\theta }_M)$ 是通过基于PointNet架构的孪生网络来实现的。基本上，孪生网络由两个分支组成，这两个分支具有完全相同的架构和相同的权重集。在每个训练元组中，正点云和负点云被馈送到这两个分支中。

2.2.2 PointNet

2D-3D MatchNet架构的第二个分支是经典的PointNet，它分为两个子网络，执行不同的任务：分类和分割。

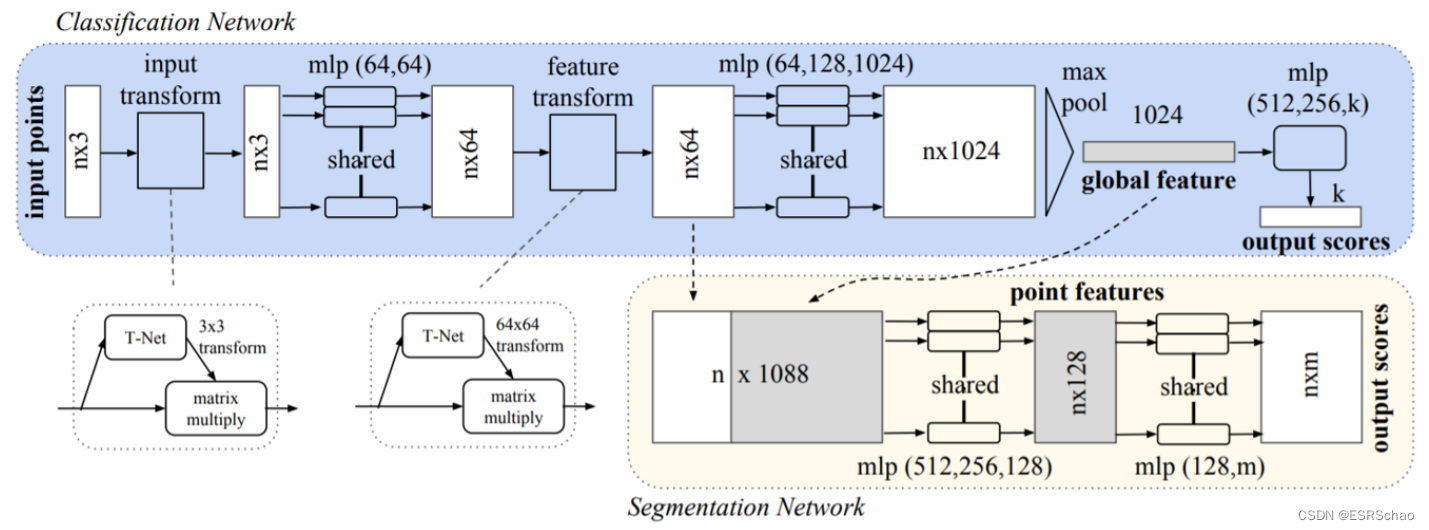
分类网络使用多层感知机将输入点云的每个输入点（具有坐标 $(x,y,z)$）映射到大小为64的更高维度的向量。该过程重复进行，直到为每个点获得大小为1024的特征。然后，通过全局最大池化将所有特征图压缩为全局特征向量，该池化层获取与每个点对应的特征图的最大值。作为最后一步，分类网络将全局特征向量调整到预定义的维度k。

点云是无结构的数据，可以表示为坐标的数字集合（也可以包括其他属性，如点的颜色）。对于具有N个点的点云，存在N!个排列方式，即可以以N!种不同的方式重新排列N个点，而不改变点云结构的几何含义。换句话说，集合中点的顺序不应影响网络的性能。因此，需要在PointNet的架构中使用符合交换律的函数，以便输入的排列不会改变计算的特征。这些函数的例子包括max$（max(a,b)=max(b,a)）$、sum$（sum(a,b)=sum(b,a)）$和average$（average(a,b)=average(b,a)）$。

子网络 “input transform” 和 “feature transform” 负责确保 PointNet 的性能不受输入数据的变换（如平移和旋转）的影响。毕竟，两个相同的点云表示相同的结构，即使其中一个经过旋转。这非常有益，因为避免了需要执行数据增强，使网络学习如何处理输入数据的变体。

“input transform” 模块由两部分组成：T-Net 和 “matrix multiply”。前者是基于多层感知机的网络，学习输入点云上的 3×3 仿射变换。在后者中，输入点云的每个点都与在 T-Net 中找到的变换相乘。这样，输入点云就被规范化为特定姿态。请注意，由于 T-Net 的性质，变换将在训练期间学习，这意味着随着训练的进行，PointNet 将对输入变换变得更加稳健。

上一段的解释可以扩展到 “feature transform” 模块。然而，这种情况下计算出的变换矩阵的大小将为 64×64，因为输入特征的大小为 N×64，其中 N 是输入点云中的点数。

2.2.3 损失函数

整个三支网络有一个唯一的损失函数定义如下：
$$\ln (1+e^{\alpha d})$$
这个损失函数被称为加权软间隔三元组损失（Weighted Soft Margin Triplet Loss），它强制使图像锚点$x_a^I$和正点云$x_M^{+}$之间的相似性$d_{\text{pos}}=d(G(x_a^I;{\theta }_I),F(x_M^{+};{\theta }_M))$较小。
此外，它试图使图像锚点和负点云$x_M^{-}$之间的距离尽可能大，以使$d(G(x_a^I;{\theta }_I),F(x_M^{+};{\theta }_M))\ll d(G(x_a^I;{\theta }_I),F(x_M^{-};{\theta }_M))$，其中$d_{\text{neg}}=d(G(x_a^I;{\theta }_I),F(x_M^{-};{\theta }_M))$。因此，在方程5中，$d=d_{\text{pos}}-d_{\text{neg}}$，$\alpha$ 是设置为5的收敛参数。
有关三元组损失的更多信息可以参见上篇博文。