小波分解、去噪、时频分析画图

目录

1.基本概念

2.Matlab函数

（1）小波分解与重构

（2）去噪

1）wden函数

2）wthresh函数

（3）画时频图

1.基本概念

小波去噪基本概念_蜘蛛侠不会飞的博客-CSDN博客_小波去噪

小波阀值去噪的基本问题包括三个方面：小波基的选择，阀值的选择，阀值函数的选择。

（1）小波基的选择：

通常我们希望所选取的小波满足以下条件：正交性、高消失矩、紧支性、对称性或反对称性。但事实上具有上述性质的小波是不可能存在的，因为小波是对称或反对称的只有Haar小波，并且高消失矩与紧支性是一对矛盾，所以在应用的时候一般选取具有紧支的小波以及根据信号的特征来选取较为合适的小波。

参考：有关小波的几个术语及常见的小波基介绍_jbb0523的博客-CSDN博客_常用小波基

（2）阀值的选择：

直接影响去噪效果的一个重要因素就是阀值的选取，不同的阀值选取将有不同的去噪效果。目前主要有无偏风险估计阈值、极大极小阈值、固定阈值、启发式阈值。

参考：小波阈值去噪_Zhi Zhao的博客-CSDN博客_小波阈值去噪原理

（3）阀值函数的选择：

阀值函数是修正小波系数的规则，不同的反之函数体现了不同的处理小波系数的策略。最常用的阀值函数有两种：一种是硬阀值函数，另一种是软阀值函数。还有一种介于软、硬阀值函数之间的Garrote函数。

参考：小波阈值去噪_Zhi Zhao的博客-CSDN博客_小波阈值去噪原理
另外，对于去噪效果好坏的评价，常用信号的信噪比（SNR）与估计信号同原始信号的均方根误差（RMSE）来判断。

2.Matlab函数

小波变换和小波阈值法去噪_红叶幽香的博客-CSDN博客_小波变换去噪

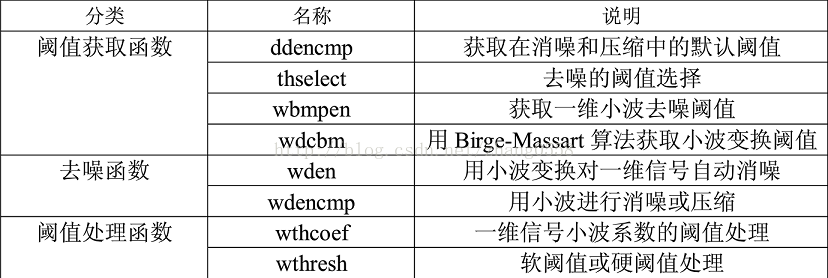
（1）小波分解与重构

小波阈值去噪_Zhi Zhao的博客-CSDN博客_小波阈值去噪原理

y=x+nt; %含噪信号
%% 用db4小波对含噪信号进行5层分解并提取系数
[c,l]=wavedec(y,5,'db4'); 
%取第5层低频近似系数
ca5=appcoef(c,l,'db4',5);
%取各层高频细节系数
cd5=detcoef(c,l,5);
cd4=detcoef(c,l,4);
cd3=detcoef(c,l,3);
cd2=detcoef(c,l,2);
cd1=detcoef(c,l,1);
thr=thselect(y,'sqtwolog'); % 阈值获取
%% 进行软阈值处理
ysoft5=wthresh(cd5,'s',thr);
ysoft4=wthresh(cd4,'s',thr);
ysoft3=wthresh(cd3,'s',thr);
ysoft2=wthresh(cd2,'s',thr);
ysoft1=wthresh(cd1,'s',thr);
c1=[ca5;ysoft5;ysoft4;ysoft3;ysoft2;ysoft1];
Y=waverec(c1,l,'db4');

以下是原始的代码段，注意wrcoef和detcoef、appcoef的区别

小波分解，wrcoef，appcoef和detcoef函数的区别_百度知道 (baidu.com)

%%小波分解：小波函数选择
[d,a]=wavedec(signal,3,'db3')       %3层db小波分解
a3=wrcoef('a',d,a,'db3',3);         %重构第3层近似系数，最低频
d3=wrcoef('d',d,a,'db3',3);         %重构第3层细节系数  
d2=wrcoef('d',d,a,'db3',2);         %重构第2层细节系数
d1=wrcoef('d',d,a,'db3',1);         %重构第1层细节系数，最高频
%%阈值选择：无偏风险估计阈值、极大极小阈值、固定阈值、启发式阈值
thre = thselect(signal,'rigrsure');
%%软阈值处理：软阈值，硬阈值以及其他改进的方法
ysoft3 = wthresh(d3,'s',thre);
ysoft2 = wthresh(d2,'s',thre);
ysoft1 = wthresh(d1,'s',thre);
%%重构
c1=[a3;ysoft3;ysoft2;ysoft1];
Y=waverec(c1,a,'db3');

（2）去噪

1）wden函数

[dnsig1,c1,l1,threshold_SURE] = wden(sig,'rigrsure','h','mln',lev,wname);

输入原始信号，输出去噪后的信号

matlab中的wden函数（Automatic 1-D Denoising Using Wavelets） - Link_kingdom - 博客园

% Using the sym8 wavelet, perform a level 5 wavelet decomposition of the signal and denoise %it by applying three different threshold selection rules to the wavelet coefficients: %SURE, minimax, and Donoho and Johnstone's universal threshold with level-dependent estimation of the noise. In each case, apply hard thresholding.
lev = 5;
wname = 'sym8';
[dnsig1,c1,l1,threshold_SURE] = wden(sig,'rigrsure','h','mln',lev,wname);
[dnsig2,c2,l2,threshold_Minimax] = wden(sig,'minimaxi','h','mln',lev,wname);
[dnsig3,c3,l3,threshold_DJ] = wden(sig,'sqtwolog','h','mln',lev,wname);
[dnsig4,c4,l4,threshold_heursure] = wden(sig,'heursure','h','mln',lev,wname);

2）wthresh函数

需要与其他函数配合使用，见1）小波分解与重构

wden 和wthresh两者去噪的区别_百度知道 (baidu.com)

（3）画时频图

clc
clear all
close all
fs = 20e3;                  % 采样频率
fn = 3e3;                   % 固有频率
y0 = 5;                      % 位移常数
g = 0.1;                     % 阻尼系数
T = 0.01;                   % 重复周期
N = 4096;                  % 采样点数
NT = round(fs*T);      % 单周期采样点数
t = 0:1/fs:(N-1)/fs;      % 采样时刻
t0 = 0:1/fs:(NT-1)/fs;  % 单周期采样时刻
K = ceil(N/NT)+1;       % 重复次数
y = [];
for i = 1:K
    y = [y,y0*exp(-g*2*pi*fn*t0).*sin(2*pi*fn*sqrt(1-g^2)*t0)];
end
y = y(1:N);
figure
cwt(y,fs);

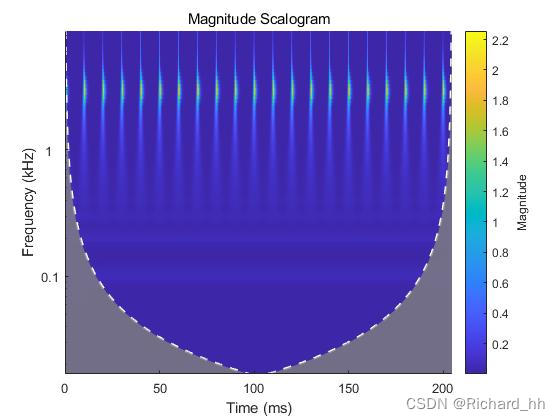
 蓝色部分为可信域