论文《基于稀疏深度的相位展开方法用于深度感知》学习_深度稀疏

A phase unwrapping method based on sparse depth for depth perception（2018 SCI 一区）

Abstract

相位模糊是三步相移相位展开的主要难点。提出了一种基于稀疏深度图的三相相移相位展开方法。稀疏深度图是深度采集的相位展开辅助工具。首先，提出了一种基于随机散斑和Delaunay三角剖分的随机网格模型。其次，基于所提出的随机网格可以计算出稀疏深度。最后，根据相对相位图(质量图)的质量，设计了相位展开序列。利用计算得到的稀疏深度作为辅助，根据设计的相位展开序列求解绝对相位。根据提出的相位展开算法，可以获得深度。在实验中，我们分别在简单场景和复杂场景中验证了所提出的相位展开算法的可靠性。该方法避免了相位模糊。实验表明，该方法在精度和分辨率上都有一定的优势。

1. 介绍

三维数字条纹投影轮廓术(DFPP)是近年来三维非接触测量领域的一个研究热点。它在物体识别、场景理解等领域具有重要的应用价值。光学三维形状测量方法具有全场、高分辨率、易于实现等优点。换句话说，虽然非接触式测量方法存在一些技术上的缺陷，但这种方法在将来会得到广泛的应用。

DFPP设置由一个投影仪和一个摄像机组成。DFPP中的投影仪被建模为一个反向摄像机[4]。编码后的图案投射到物体表面[5]上，由CCD摄像机记录下产生的条纹图案。在各种条纹图分析方法中，移位法具有速度快、分辨率高、精度高等优点。该方法对环境光照和表面反照率的变化具有较强的鲁棒性。然而，由于移相法相位展开过程中误差的传播，使得绝对相位计算技术仍然存在相位误差。

相位模糊是三步相移相位展开的主要难点。而在地表突变或需要对多个孤立物体进行模拟测量时，仅利用相机采集的三相图像很难提取绝对相位。解决这一问题的方法有:将阶梯图[7]、码字图[8]或稀疏深度图[9]嵌入相移。

阶梯图案的设计使楼梯的变化与相对相位序数完全一致，参考楼梯图案可以恢复绝对相位。该码字被嵌入相位，然后用于确定相对相位序数。将稀疏深度模式嵌入到边缘模式中，实现精确的三维动态传感。在不增加图像的情况下，该方法可以解决复杂场景的相位模糊问题。相对相位序数是一个方向(水平或垂直)的相位数。一个相位周期被定义为一个序数，因此每个相位都被编号。通过计算相对相位图中的相对相位序数，可以得到绝对相位图。

在相移中嵌入灰度编码模式的方法对于高对比度的曲面测量不具有鲁棒性，因为灰度编码方法是根据图像的强度而不是相位来确定编码。提出了一种将码字嵌入相移计算绝对相位的方法。具体地说，在投影一组相移模式后，投影一条灰度梯度条纹，在每一个相位上是不同的，在相邻相位的灰度上有一个梯度，就像不同相位的码字一样。同样，这种方法也受到目标对比度的影响。

基于稀疏深度的相位展开方法是在相对相位图中计算相对相位序数。随机散斑图是求解稀疏深度的一种传统方法。随机散斑图案是Kinect中使用的一种单点图案[10]。这与嵌入灰度编码模式相同，灰度编码模式还可以嵌入到相移中，以帮助求解绝对相位。在实际应用中也取得了理想的效果。然而，一些散斑被遮挡并覆盖在复杂或对比的场景中，导致该区域的测量孔，绝对相位解仍然保持误差[11]。

相对相位图的质量可以用来确定相位展开序列。自回归(AR)模型已经在许多图像处理应用中得到了应用，如果AR预测器设计得当，简单的AR模型在许多应用中是通用的。利用AR模型，可以较准确地描述相对相位图的质量。AR模型的设计利用了原始相对相位图像与计算出的质量图之间的相关性。在此基础上设计了相位展开序列。展开路径从质量最高的点开始，并继续到质量较低的点。当相位沿质量路径展开时，可以避免误差传播，而传统的展开路径则不能。

本文在随机散斑和Delaunay三角剖分的基础上提出了随机网格模式[12]。这种随机网格可以看作是随机散斑和线结构光的组合。每一点都是一组线的汇合点。随机网格保持了随机散斑的所有优点，由于其具有更多的匹配信息，所以在匹配方面随机网格比随机散斑更加精确。点的位置可以由随机点被阻塞的区域中的几行信息推断出来。因此，我们提出了一种基于变形线曲率和挠度的深度测量算法。

根据相对相位图的质量顺序，提出了一种基于稀疏深度图的相位展开方法。相位模糊是三步相移相位解缠的主要难点。稀疏深度图被应用于密集深度图获取的相位展开中。为了获得稠密的深度信息，相位展开序列以相对相位图的质量为指导。基于随机网格的计算稀疏深度作为辅助，根据设计的序列来求解绝对相位，以获得相对较少图案的精确3D感测。
论文组织如下:第2节阐述了提出的系统原理和设计模式;第3节给出了相位展开算法的框架;第4节给出了实验结果;第5节讨论了该方法的局限性和优点。

2. 系统组成及校正

2.1. 提出了一种光学三维形状测量系统

该装置的主要目的是检索深度信息，设计的系统由一个图像投影仪设备和一个图像捕获设备组成，如图1所示。对于图像采集，图像采集设备是一个高清晰度为3224×2448的USB摄像头，最大帧频为60fps。该装置的DLP投影仪是TI Light Commander，集成了DMD技术，分辨率为1920*1080。对于8位灰度图像，这种可编程投影仪的帧频高达700hz。虽然这两种设备的分辨率不同，但足以达到高分辨率的目的。实验中的DFPP设置如下：

投影仪和相机在水平方向上严格对准，垂直相移条纹图案被投影，所以在水平方向上发生图案移动只是为了方便三角化。

这两套装置可以用传统的标定方法标定成一个通用的坐标系。利用普通PC进行模式生成深度重构。我们的方法是先投影四组图案，然后系统依次捕获四幅图像，其中三幅为三步相移，另一幅为随机网格。它们的融合产生了准确、鲁棒、高分辨率、低延迟的深度。

2.2. 系统校准

张的这种标定方法在结构光系统[15]的标定中得到了广泛的应用。即使没有三维几何或计算机视觉的专业知识，也可以使用这种方法。它只需要一个摄像头就可以观察到一个平面的校准模式，显示在几个(至少两个)不同的方向。结构光系统或平面校准模式可自由移动。该方法在考虑透镜畸变的情况下，通过基于极大似然准则的非线性优化改进了结构光系统的测量结果。校准结果见表1和表2。

使用MATLAB中常用的摄像机标定工具箱对投影仪和摄像机进行标定。在投影仪标定过程中，无法获得投影图像的像素值，这只是放大效应的一种衍射。从理论上讲，投影仪的投影符合针孔模型。

3. 提出了相位展开方法

三步相移法由于具有计算复杂度高、速度快、精度高等优点，在三维测量中得到了广泛的应用。相位模糊问题通常发生在有突变的表面或需要同时测量多个孤立物时，所测量的绝对相位误差如图3所示，仅基于所获得的相移图像。因此，求解k值是相位展开的关键部分。

虽然可能存在误差，但可以采用某种算法来实现相位展开计算结果的实时化。相移技术无论是三步法还是多步法都不可能从理论上解决相移模糊问题。为此，将辅助图像嵌入到三步相移模式中，提高了测量精度。在三步相移中，用稀疏深度作为辅助提取绝对相位。为了获得更准确的深度信息，根据三步模式得到的相对相位图的质量确定相位检索序列。

在本文中，我们设计了基于随机散斑的随机网格模式。设计模式和使用的散斑模式的区别在于，线模式被添加到散斑上。利用直线信息，将随机网格模式投射到目标上，并由摄像机捕获，可以计算出准确的散斑位置信息。选择随机网格的目的是计算稀疏深度。以基于随机网格的稀疏深度计算为辅助，求解绝对相位符合设计序列。该方法避免了相位模糊。

本文通过投影仪将四幅图像依次投影到曲面形状上，并由摄像机进行拍摄，其中三幅为三步相移，另一幅为随机网格。提出了一种基于随机散斑和Delaunay三角关系的随机网格算法。以基于随机网格的稀疏深度计算为辅助求解绝对相位。通过这种方法可以避免相位变大。

因此，我们的技术路线如图2和表3所示。

3.1. 设计图案

在我们的投影程序中，四种模式被投影到对象上，相应的，系统依次捕获四幅图像，其中三幅为三步相移，另一幅为随机网格。

三步移相模式以其速度和精度在光学计量中得到了广泛的应用[14]。投影仪以2/3$\pi$的相移将三个相移图形投影到场景中。从数学上讲，相机捕捉到的相应图像可以表示为等式1。

我们将基于Delaunay三角测量算法[15]的Kinect V1中的随机散斑连接起来。如上所述，在Kinect V1中使用了随机散斑模式，因为它具有很高的局部可分辨性和易于实现。但在某些情况下，斑点可能会被遮蔽。当光的作用更强时，它很容易消失。由于散斑获得的深度信息是稀疏的，所以很难求出绝对相位。也就是说，某些区域的绝对相位不能得到散斑深度的参考。在这种情况下，如果散斑被遮挡，稀疏深度图的空洞将被放大。

在光学领域中，散斑是一种由相干光源在粗糙表面上反射的干涉现象。因此，一般采用人工散斑来模拟真实散斑。正因为这样更容易制作。产生散斑的原理如下:

1. 散斑图中的每个点都是k×k像素的平方，像素的数量由投影仪的分辨率和三步相移的振幅决定。
2. 正方形区域只有一个点，相当于3×3点。
3. 这些点是随机分布的，在八个邻域中没有两个点是相邻的。

随机散斑的产生原理如下图所示，类似于Microsoft Kinect V1的模式。该算法首先构造了一个所有支持点都被包围的超三角形。三角网格内分散的点依次插入。当插入点被一个三角形外圆包围时，三角形的公共侧将被重新移动。

然后将插入点连接到三角形的所有点上，形成一个Delaunay三角形网格。并根据优化准则[17]对其进行优化，直到所有的离散点都是三角形的。以上图4为基于随机散斑的Delaunay三角网及其外切圆。

图5所示的随机网格模式是基于这组随机散斑与上述Delaunay三角剖分组合而成的。在实际应用中，与电磁顺层码字和灰度编码方法相似，随机网格中的散斑分布必须小于相位幅值，否则无法从理论上解决相位模糊问题。

3.2。基于随机网格的稀疏深度图计算

稀疏深度是空间中离散的深度信息。稀疏深度图可以通过多种方式获得。采用随机网格法计算稀疏深度图。在我们的算法中，随机网格被设计成嵌入到相移模式中，以优化相位展开的结果。

摄像机得到的随机网格图案在投射到场景中时发生变形。传统的方法是打开一个小的滑动窗口来扫描捕获的图像，并将其与提取的图像进行比较。相关参数用于定位对应点和测量位移。然后通过三角剖分得到投影图像和捕获图像之间的偏移来获得深度图。在稀疏深度测量系统中，用随机网格模式代替随机斑点模式。随机网格中的直线信息不仅可以帮助我们定位被障碍物遮挡的灭点，而且可以优化传统三角法计算的深度。

具体来说，在消失点的位置方面，由于透视或遮挡的原因，通过投影仪的投影，散斑会在获得的随机网格图像中丢失。这种现象如图6所示。

通过对摄像机得到的线拓扑网络的分析，可以得到由于遮挡而消失的散斑。公式如下：

其中$p(x,y)$表示消失散斑的位置。$s_{●}$是在获得的图像中，围绕该点的这些线的数目。n表示mth随机散斑处的向外辐射线的数目。只有当围绕该点的线的数目大于或等于3时，才确定该点处存在消失的散斑。

经过形态处理后，将少量的离散点聚集在一起，得到变形的随机散斑图。因此，可以通过比较所有交点相对于投影散斑图的位移来计算每个散斑的深度。

如果系统校准准确，深度可以根据三角测量来计算。

其中$v_{●}$分别为摄像机和投影仪中物体的坐标值，$f_{●}$为其相应的固有参数。而$t_y$是外部参数。

在计算深度值优化方面，我们的算法考虑了原网格中直线的挠度。在得到的随机网格中，由于如图7 (a)所示的变形，直线可以变为折线或曲线。首先根据传统的三角剖分方法得到粗深度图。然后查看图7 (b)和©所示网格中各点周围的曲线和直线，根据曲线和曲线计算扇形的面积。

在我们的算法中，为了计算出面积和相对深度变化的关系，中心点和周围点可以分成四个区域。当一个点位于中心点的右上角时，如果直线向上弯曲(即红线)，则中心点比右上角的点高(中心点比右上角的点更接近参考平面)。在这种情况下，我们认为在每个维度上，它都是线性变化的。理论上，面积与相对高度和投影仪的内部参数成正比，与外部参数和相机的内部参数成反比。因此由p1和p2组成的区域的面积可以表示为：

式中:$f_{●}$为摄像机和投影仪沿x、y轴的固有参数。t:为系统沿两轴的外部参数。h为点p1与点p2的相对高度，k为正、负值随方向变化的系数。(u,v)表示计算出的中心点的坐标值。

为了计算相对高度，公式5可改写为

相对高度计算的目的是优化根据三角剖分算法计算出的深度结果d (u,v)。使用全局优化算法获得最优深度值，其表达式为:

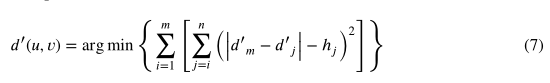
其中d '是d的优化结果，使得(u,v)处的方差最小。该优化的稀疏深度图可用于三步相移法的绝对相位求解。

3.3、相位展开顺序的设计

所提出的相位展开序列通常是在一个方向上（水平或垂直）。相位模糊问题常发生在表面突变或多个孤立目标的情况下。在突出部分，相变质量高。相反，弛豫部分的相变质量较低。这些质量图可用于确定相位展开序列。

在获得的相对相位图像中，良好相位的灰度值由0变为255。由于畸变，这种变化可能是非线性的，但在一个像素的八个或八个以上邻域范围内，必须是一定方向上的梯度。这种类型的点被定义为高质量的点。如果所有的高质量点都能实现连接，就会找到所有点相位确定的依据。然后求出绝对相位。基于这一思想，我们提出了一种拉普拉斯滤波器作为判别算子：

自回归(AR)模型在图像处理中得到了广泛的应用，如图像序列中缺失区域的检测和插值、超分辨率、时空数据预测等。这表明，如果AR预测器设计合理，简单的AR模型在许多应用中是通用的。利用AR模型，可以准确地描述相图的质量。AR模型的设计利用了原始相对相位图像与计算出的质量图之间的相关性。在此基础上设计了相位展开序列。

一般来说，基于AR模型可以很好地描述相对相位图的这种性质。

其中D是基于原始相对相位图和判别算子L计算的质量图。D0观测质量图。$E_{data}$是使恢复质量图与观测值一致的数据项，$E_{AR}$是将AR模型强加于恢复质量图上的AR项。数据项和AR项由权重$\lambda$关联。一般来说，具有不同预测器的AR模型具有不同的性能，在AR模型的基础上将图像分割成多个小单元。该预测器在每个单元中共享。
由于上述原因，影响了恢复后的质量图的准确性和分辨率。因此，设计了一种鲁棒的逐像素AR模型预测器:

其中$d_0$是基于$D_0$的双三次插值的粗略估计的质量图。$d_0$的分辨率与高分辨率相对相位图像一致。而$S_x$是归一化因子。质量项的设计是为了利用原始相对相位图像和计算出的质量图中的相关性。式11中计算出的质量项和原始相对相位项可计算如下：


实验中，图8分别测试了3×3,5×5，…，19×19的邻域。实验表明，随着邻域的扩展，更多的样本被选择到AR预测器中，在恢复的质量图中产生了更稳定的结果。

但当邻域数超过11×11时，质量恢复图中随邻域数增加而增加的趋势不明显，但计算复杂度明显增加。因此，在实验中选取11×11的邻域。

为了测量各参数对恢复后的质量地图质量的影响，在11×11邻域随机选取质量地图。对参数空间进行遍历，分析各参数的敏感性及其自适应特性，在固定的合理值下，确定质量恢复函数中各参数的合理值:

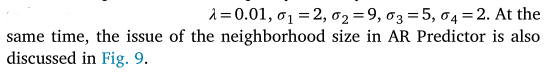
3.4、基于稀疏深度的相位展开

为了提高高质量像素点的连通性，基于上述算子计算形态梯度。打开滑动窗口，根据邻域像素灰度值计算相对相位的质量，如下图所示:

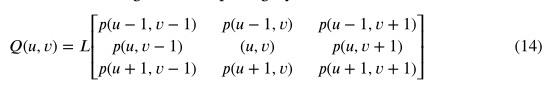
由于三步相移模式和随机网格模式都来自同一个系统，因此像素之间的对应关系不需要校准。相位序数k (u,v)和稀疏深度d (u,v)在同一像素点上考虑，从而计算出k。

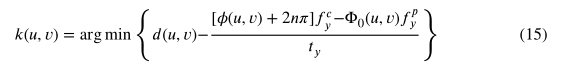
由于d是稀疏的，k不能用像素来计算。在我们的算法中，随机网格的点间距小于相位幅值，这样就可以利用足够的数据来标记相位，从而得到绝对相位。下面的图10是一个例子。

这种相位展开方法可以减少累积误差，就像根生长在许多方向上一样。计算每个像素处的相位质量来指导绝对相位的展开。算法中相位展开的顺序总是沿着高质量点到低质量点的方向进行。这种方法可以减少误差的传播现象。

4. 实验结果与分析

在这一部分中，我们通过各种场景进行实验，对随机网格、ToF、三步相移法和我们的方法计算出的深度图的质量进行评估。

4.1、定性分析

实验中首先测试了三个场景简单的目标（棋盘、方盒和简单石膏模型）。用棋盘格平面测试了实验结果对物体反射率的灵敏度。在第二组简单场景实验中，以一个方形盒子为例。这个物体由几个面组成，每个面都有许多不同的颜色。在第三组简单场景实验中，以一个简单的石膏模型为例。

由于我们的第一个目标是一个棋盘格平面，水平深度值应该是线性变化的，根据这个准则，四组实验结果如下图所示。在实验中，我们将实验结果与嵌入码字法、嵌入灰度编码法和嵌入随机斑点法进行了比较。

虽然在本实验中，灰度编码方法的嵌入没有受到反射率的显著影响，但在图11 (b)中间的小累积误差仍然明显。我们测量的深度图主要来自三步相移，随机网格只是辅助，测量结果很少受到反射率的影响。图11 (a)所示的码字法、图11 (c )所示的随机散斑法以及图11 (d)所示的我们所提出的方法在棋盘格平面测量的平稳性方面表现良好。

在第二个简单场景的实验中，由于方框的面是一个平面，因此本实验仍然保持了线性特性。根据这一准则，四组实验结果如下所示。图12 (a)的实验结果表明，嵌入码字法得到的深度仍然受到反射率的影响。图12 (b)所示的灰度编码方法嵌入时仍产生累积误差。这个盒子在这个实验中是光滑容易形成镜面反射,噪声点很容易嵌入随机产生的斑点图12所示©方法。如预期在图12 (d),实验结果显示三步相移和随机网格的互补特征。

在第三个简单场景的实验中，平面的过渡效果是主要的测试目标，四组实验结果如下图所示。

由于石膏的反射能力较弱，图13 (a)中的码字法和图13 ©中的随机散斑法的嵌入效果较好。相反，由于边界复杂，图13 (b)所示的灰度编码方法嵌入效果不佳。形状变化是影响测量结果的主要因素。实验结果表明，在图13 (b)中平面并不平坦，其他结果更好。因此，我们的方法克服了容易引起形状变化的相位模糊的累积误差，如图13 (d)所示。

在接下来的实验中，我们尝试了复杂的场景。一些服装被用来构造一个复杂的凸物体。在深度图中，灰度越深，相对于相机的距离越近。实验结果如图14所示。

图14 (a)所示的码字嵌入法测量的实验结果存在明显的误差，与其他测量相比，图14 (b)所示的灰度编码方法仍然容易发生相移。当被测物体存在颜色多样性时，基于灰度编码方法的深度图仍然存在相位误差。嵌入随机散斑方法不能避免图16（c）所示的边缘处的噪声点的误差。由于优势互补，我们的结果有效地结合了图16（d）所示的三步相移和随机网格的优势。此外，我们的算法的稳健性明显高于上述其他方案。

4.2、定量评价

为了更严格、更全面的定量评估，我们比较了基于嵌入模式的相位展开、基于码字模式的相位展开、基于灰度编码模式的相位展开以及我们的方法的实验结果。我们还比较了几种基于稀疏深度的相位展开方法（随机散斑和我们的方法）。

从理论上讲，水平深度值应该是线性变化的，根据这一准则，五组实验结果如下图所示。对棋盘格平面进行测试，定量评价实验结果如图15所示。

在实验中，我们比较了几种方法:无嵌入模式的相位展开法、码字法、灰度法、随机斑点法和我们的方法。实验表明，无嵌套相位展开法与嵌套相位展开法相比有明显的误差。虽然平面内的误差不显著，但随着深度的增加误差逐渐增大。

为了更严谨和全面的定量评估，我们比较了不同方法的性能，包括三步相移和我们的方法。换句话说，对于每一个放置在不同深度的倾斜平面，每种方法都要测量十次以上。在每个深度上，对三维点进行一个平面的拟合，计算重构点与拟合平面的均方根重构误差。

在定量均方根误差测量中，这个斜面被定义为一个平面。倾斜面可以用最小二乘法计算。当表面更复杂时，超曲面的拟合复杂度增加，合理的平均高度不能适当地拟合。我们的拟合方法不是基于所有的点，而是基于每个点的邻域，拟合每个点的邻域均值。

定量结果如图16所示，与其他方法相比，我们的方法具有更高的准确性。所有方法的性能都会随着深度的增加而逐渐降低。原因是，相同的视差对应的深度范围更大，距离更远。由于定量评价只能基于正则图，因此不能直观地展示我们方法的优点。但我们的实验结果在数字上仍然比其他方法更准确。

5. 结论

本文基于Delaunay三角剖分算法，将传统的随机散斑连接起来。该随机网格用于求解三步移相中的绝对相位。我们的方法是通用的，除了一套结构光设备（一台投影仪和一台摄像机）外，不需要额外的设备。四幅图像依次拍摄（三幅用于三步相移，另一幅用于随机网格）。基于三幅相移图像得到相对相位，利用随机网格模式测量稀疏深度。提出了一种新的绝对相位恢复算法。稀疏深度作为辅助求解绝对相位。这种方法可以避免相位模糊。为了获得更准确的深度信息，根据质量图确定相位恢复序列。