- 1初学C语言-二维数组与字符数组_二维数组和字符数组
- 2Android Studio 报错:Could not determine the dependencies of task ‘...‘.Installed Build Tools revision_could not determine the dependencies of task ':app
- 3【Android】常用对话框大全(三)自定义Dialog的三种方式(Theme,PopupWindow,Dialog)_android dialog theme
- 4js 获取一周前或一个月前的时间戳_js获取一个月之前的时间戳
- 5鸿蒙应用开发 -Web 组件使用_鸿蒙开发web js组件页面
- 6国内AI大模型网址大全
- 7Java:比较版本号_java version比较
- 8Mysql8.0配置问题_how to change mysql 8.0 user plugin
- 9带你跳出H5输入框input的坑_android h5 只能删除 不能输入
- 10在ArcGIS上使用python(arcpy包)的入门教程_arcgis python
对LCA、树上倍增、树链剖分(重链剖分&长链剖分)和LCT(Link-Cut Tree)的学习_树链剖分与lct
赞
踩
LCA
what is LCA & what can LCA do
LCA(Lowest Common Ancestors),即最近公共祖先
在一棵树上,两个节点的深度最浅的公共祖先就是 L C A LCA LCA (自己可以是自己的祖先)
很简单,我们可以快速地进入正题了
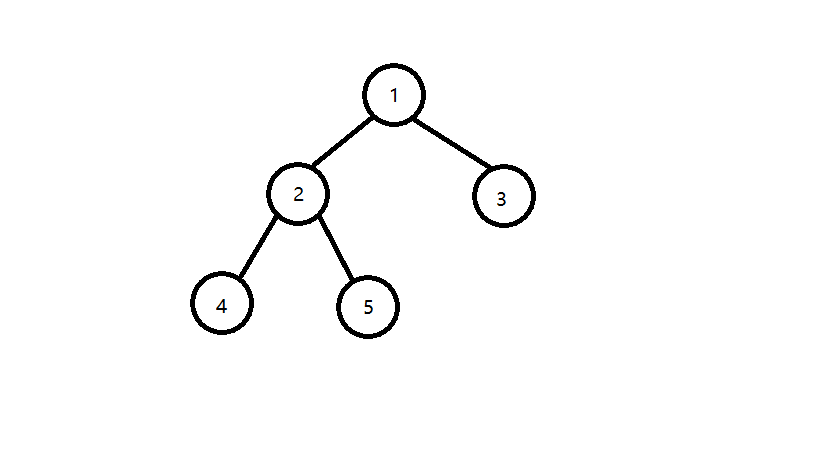
下图中的树, 4 4 4和 5 5 5的 L C A LCA LCA为2, 1 1 1和 3 3 3的 L C A LCA LCA是1(1也算1的祖先)
除了是直接求两点的 L C A LCA LCA的模板题,没有题目会叫你打个模板
那么LCA能干嘛?
其实 L C A LCA LCA的用途很广,感觉用 L C A LCA LCA最多的像是这样子的题
-
给你一棵树
(或者是一个图求完MST,这很常见)和树上的两点 -
然后找出这两点之间的路径的极值或权值和或其他东东
这时我们可以借助这两点的LCA作为中转点来轻松地解决这类题目
how to discover LCA
还是这棵树
4 4 4和 3 3 3的 L C A LCA LCA是1,这两点间的路径是下图标红的路径
怎么求LCA呢?
method one
暴力dfs一遍,时间复杂度 O ( n ) O(n) O(n)
侮辱智商
(逃)
method two
模拟,从两点开始一起向上跳一步,跳过的点标记一下,时间复杂度 O ( n ) O(n) O(n)
侮辱智商*2
(逃)
method three
用dfs记录每个点的深度,求 L C A LCA LCA时先调至统一深度,再一起向上跳
如果这棵树是一个刚好分成两叉的树,时间复杂度 O ( n ) O(n) O(n)
侮辱智商*3
(逃)
上面的都是小学生都会的东西,不必讲了
想真正用有意义的 L C A LCA LCA,下面才是重点
tarjan算法(离线)求LCA
求 L C A LCA LCA有一种非常容易理解的方法就是tarjan算法预处理离线解决,时间复杂度 O ( n + q ) O(n+q) O(n+q),飞速
仍感觉离线算法不适用于所有题目
(比如某些良心出题人丧病地要你强制在线,GG)
反正在线算法可以解决离线能做出来所有的题
所以,我不讲 t a r j a n tarjan tarjan求 L C A LCA LCA了,推荐一篇写的很棒的blog
接下来的几个在线算法才是搞 L C A LCA LCA的门槛
ST(RMQ)算法(在线)求LCA
这种方法的思想,就是将LCA问题转化成RMQ问题
- 如果不会 R M Q RMQ RMQ问题—— S T ST ST算法的就戳这里吧
可以转化成RMQ问题?
这里有棵树
如何预处理呢?
我们用dfs遍历一次,得到一个 d f s dfs dfs序(儿子节点回到父亲节点还要再算一遍)
d f s dfs dfs序就是这样的1->2->4->7->4->8->4->2->5->2->6->9->6->10->6->2->1->3->1
(一开始在 r o o t root root向儿子节点走,到了叶子节点就向另一个儿子走,最后回到 r o o t root root)
d f s dfs dfs预处理的时间复杂度为 O ( n ) O(n) O(n)
dfs序妙啊
设 r [ x ] r[x] r[x]表示 x x x在 d f s dfs dfs序当中第一次出现的位置, d e p t h [ x ] depth[x] depth[x]表示 x x x的深度
如果求 x x x和 y y y的 L C A LCA LCA,r[x]~r[y]这一段区间内一定有 L C A ( x , y ) LCA(x,y) LCA(x,y),而且一定是区间中深度最小的那个点
(比如上面的dfs序中,第一个 7 7 7和第一个 5 5 5之间的序列里的深度最小的点是 2 2 2,而 2 2 2正是 7 7 7和 5 5 5的 L C A LCA LCA!)
-
遍历以 L C A ( x , y ) LCA(x,y) LCA(x,y)为根的树时,不遍历完所有以 L C A ( x , y ) LCA(x,y) LCA(x,y)为根的树的节点是不会回到 L C A ( x , y ) LCA(x,y) LCA(x,y)的
-
还有就是明显地,想到达x再到y,必须上溯经过它们的LCA(两个点之间有且只有一条路径)
-
所以 L C A LCA LCA的深度一定最小
直接用RMQ——ST表维护这个东西,求出来的最小值的点即为 L C A LCA LCA
matters need attention
-
d f s dfs dfs序的长度是 2 n − 1 2n-1 2n−1,用 d f s O ( n ) dfsO(n) dfsO(n)处理出 r r r、 d e p t h depth depth和 d f s dfs dfs序之后直接套上裸的 R M Q RMQ RMQ
-
设 f [ i ] [ j ] f[i][j] f[i][j]表示dfs序中j~j+2^i-1的点当中,depth值最小的是哪个点 即可
-
那么单次询问时间复杂度 O ( 1 ) O(1) O(1)
-
完美
code
这段代码是我co过来的,因为我也是看别人博客学的
但这代码是真的丑
#include <cstdio> #include <cstring> #include <cmath> using namespace std; int n,_n,m,s;//_n是用来放元素进dfs序里,最终_n=2n-1 struct EDGE { int to; EDGE* las; }e[1000001];//前向星存边 EDGE* last[500001]; int sx[1000001];//顺序,为dfs序 int f[21][1000001];//用于ST算法 int deep[500001];//深度 int r[500001];//第一次出现的位置 int min(int x,int y) { return deep[x]<deep[y]?x:y; } void dfs(int t,int fa,int de) { sx[++_n]=t; r[t]=_n; deep[t]=de; EDGE*ei; for (ei=last[t];ei;ei=ei->las) if (ei->to!=fa) { dfs(ei->to,t,de+1); sx[++_n]=t; } } int query(int l,int r) { if (l>r) { //交换 l^=r; r^=l; l^=r; } int k=int(log2(r-l+1)); return min(f[k][l],f[k][r-(1<<k)+1]); } int main() { scanf("%d%d%d",&n,&m,&s); int j=0,x,y; for (int i=1;i<n;++i) { scanf("%d%d",&x,&y); e[++j]={ y,last[x]}; last[x]=e+j; e[++j]={ x,last[y]}; last[y]=e+j; } dfs(s,0,0); //以下是ST算法 for (int i=1;i<=_n;++i)f[0][i]=sx[i]; int ni=int(log2(_n)),nj,tmp; for (int i=1;i<=ni;++i) { nj=_n+1-(1<<i); tmp=1<<i-1; for (j=1;j<=nj;++j) f[i][j]=min(f[i-1][j],f[i-1][j+tmp]); } //以下是询问,对于每次询问,可以O(1)回答 while (m--) { scanf("%d%d",&x,&y); printf("%d\n",query(r[x],r[y])); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
小结
基础的 L C A LCA LCA知识你应该已经会了吧
L C A LCA LCA的运用挺广吧,感觉和线段树的考频有的一比,不掌握是会吃亏的
上面的是比较普通的方法求 L C A LCA LCA,其实树上倍增也能求 L C A LCA LCA
接下来到丧心病狂 (其实很简单) 的树上倍增了
树上倍增
又是什么东东?
倍增这个东东严格来说就是种思想,只可意会不可言传
倍增,是根据已经得到了的信息,将考虑的范围扩大,从而加速操作的一种思想
使用了倍增思想的算法有
- 归并排序
- 快速幂
- 基于ST表的RMQ算法
- 树上倍增找LCA等
- FFT、后缀数组等高级算法
- …… F F T FFT FFT有倍增的么……我可能学了假的 F F T FFT FFT
some advantages
树上倍增和 R M Q RMQ RMQ是比较相似的,都采用了二进制的思想,所以时空复杂度低
其实树上倍增和树链剖分在树题里面都用的很多
-
两个都十分有趣,但倍增有着显而易见的优点——
-
比起树链剖分,树上倍增代码短,查错方便,时空复杂度优(都是 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n))
-
只是功能欠缺了一些不要太在意
即使如此,树上倍增也能够解决大部分的树型题目反正两个都要学
树上倍增(在线)求LCA
preparation
怎么样预处理以达到在线单次询问 O ( l o g 2 n ) O(log_2n) O(log2n)的时间呢?
我们需要构造倍增数组
-
设 a n c [ i ] [ j ] anc[i][j] anc[i][j]表示i节点的第2^j个祖先
-
注意 a n c anc anc数组开到 a n c [ n ] [ l o g 2 n ] anc[n][log_2n] anc[n][log2n],因为树上任意一点最多有 2 l o g 2 n 2^{log_2n} 2log2n个祖先
-
可以发现这个东西可以代替不路径压缩的并查集, ∵ a n c [ i ] [ 0 ] = f a t h e r ( i ) ∵anc[i][0]=father(i) ∵anc[i][0]=father(i)
(若 a n c [ i ] [ j ] = 0 anc[i][j]=0 anc[i][j]=0则说明 i i i的第 2 j 2^j 2j祖先不存在)
然后,倍增的性质 (DP方程) 就清楚地出来了 a n c [ i ] [ j ] = a n c [ a n c [ i ] [ j − 1 ] ] [ j − 1 ] anc[i][j]=anc[anc[i][j-1]][j-1] anc[i][j]=anc[anc[i][j−1]][j−1]
-
用文字来表达它就是这样的
-
i的第 2 j 2^j 2j个父亲是i的第 2 j − 1 2^{j-1} 2j−1个父亲的第 2 j − 1 2^{j-1} 2j−1个父亲
-
神奇不?
就是说暴力求 i i i的第 k k k个祖先的时间复杂度是 O ( k ) O(k) O(k),现在变成了 O ( l o g 2 k ) O(log_2k) O(log2k)
同时,用一个dfs处理出每个点的深度 d e p t h [ x ] depth[x] depth[x]和 a n c [ x ] [ 0 ] anc[x][0] anc[x][0],时间复杂度 O ( n ) O(n) O(n)
预处理的时间复杂度即为 O ( n log 2 n ) O(n\log_2n) O(nlog2n)
code
procedure dfs(x,y:longint); var now:longint; begin now:=last[x]; while now<>0 do begin if b[now]<>y then begin anc[b[now],0]:=x; depth[b[now]]:=depth[x]+1; dfs(b[now],x); end; now:=next[now]; end; end;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
for j:=1 to trunc(ln(n)/ln(2)) do
for i:=1 to n do
anc[i,j]:=anc[anc[i,j-1],j-1];
- 1
- 2
- 3
query
请务必认认真真地阅读以下内容否则树上倍增你就学不会了
树上倍增的运用中,最简单最实用的就是求 L C A LCA LCA了
- 现在我们需要求出 L C A ( x , y ) LCA(x,y) LCA(x,y),怎么倍增做?
还记得前面三种脑残 O ( n ) O(n) O(n)求 L C A LCA LCA的第三个方法吗?
用dfs记录每个点的深度,求LCA时先调至统一深度,再一起向上跳
其实树上倍增运用的就是这个思想!只不过时间复杂度降至了飞快的 O ( log 2 n ) O(\log_2n) O(log2n)
-
对于两个节点 u u u和 v v v,我们先把 u u u和 v v v调至同一深度
-
若此时 u = v u=v u=v,那么原来两点的 L C A LCA LCA即为当前点
-
如果 d e p t h [ u ] = d e p t h [ v ] depth[u]=depth[v] depth[u]=depth[v]但 u ≠ v u≠v u̸=v,就说明 L C A ( u , v ) LCA(u,v) LCA(u,v)在更浅的地方
-
我们同时把 u u u和 v v v向上跳 2 k 2^k 2k步( k = l o g 2 d e p t h [ u ] k=log_2depth[u] k=log2depth[u]),直到 u = v u=v u=v
明显这种方法肯定能求出 L C A LCA LCA,因为 u u u和 v v v一定会相遇
倍增比那种脑残方法优的是,脑残方法一步一步向上跳,倍增一次跳 2 k 2^k 2k步!
- 但还存在着一些问题——如果这样跳,跳到了 L C A LCA LCA的祖先节点怎么搞?
所以如果 u u u和 v v v向上跳 2 k 2^k 2k步到达的节点相同,那我们就不跳,让 u u u和 v v v的第 2 k 2^k 2k祖先不同即可跳
注意每下一次向上跳的距离是上一次跳的 1 2 1 \over 2 21( k = k − 1 k=k-1 k=k−1),直到 u = v u=v u=v, L C A LCA LCA即已被求出
这样使 u u u和 v v v与 L C A LCA LCA的距离每次缩短一半,时间复杂度也就是 O ( log 2 n ) O(\log_2n) O(log2n)的
最后如何把 u u u和 v v v调至同一深度?
其实是一样的,先把较深的那个点调浅就行了
code
- 觉得上面说得抽象的话见标理解一下
function lca(x,y:longint):longint; var k:longint; begin if depth[x]<depth[y] then swap(x,y); k:=trunc(ln(depth[x]-depth[y]+1)/ln(2)); while k>=0 do begin if depth[anc[x,k]]>depth[y] then x:=anc[x,k]; dec(k); end; if depth[x]<>depth[y] then x:=anc[x,0]; k:=trunc(ln(d[x])/ln(2)); while k>=0 do begin if anc[x,k]<>anc[y,k] then begin x:=anc[x,k]; y:=anc[y,k]; end; dec(k); end; exit(x); end;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
以上三段 c o d e code code已经能解决树上倍增求 L C A LCA LCA了
树上倍增求 L C A LCA LCA的时间复杂度为 O ( n log 2 n + q log 2 n ) O(n\log_2n+q\log_2n) O(nlog2n+qlog2n)
树上倍增的真正意义
比赛里面直接求 L C A LCA LCA是没有什么用处的
其实,树上倍增的真正可怕之处是这个倍增的思想
- 不信? 来看看这种很常见的题目
给你一棵树和两个点 x x x和 y y y,求这两点间路径的路径最大/小的点权/边权
明显我们要先求 x x x和 y y y的 L C A LCA LCA,因为唯一路径必须经过 L C A LCA LCA
求 L C A LCA LCA比如说用 R M Q RMQ RMQ,然后呢?暴力 O ( n ) O(n) O(n)再遍历一次路径?
不可能的
-
这种问题用树上倍增还是能用 O ( log 2 n ) O(\log_2n) O(log2n)的时间解决
-
我们可以设 d i s [ i ] [ j ] dis[i][j] dis[i][j]表示i到他的第 2 j 2^j 2j个祖先的路径最大值,就可以边求 L C A LCA LCA边顺便求出两点距离
-
因为 d i s dis dis也符合
d i s [ i ] [ j ] = m a x ( d i s [ i ] [ j − 1 ] , d i s [ a n c [ i ] [ j − 1 ] ] [ j − 1 ] ) dis[i][j]=max(dis[i][j-1],dis[anc[i][j-1]][j-1]) dis[i][j]=max(dis[i][j−1],dis[anc[i][j−1]][j−1])
还有求两点的路径上路径权值和呢?
- 设 s u m [ i ] [ j ] sum[i][j] sum[i][j]表示i到他的第 2 j 2^j 2j个祖先的路径权值和,同时也可边求 L C A LCA LCA边求和,因为
s u m [ i ] [ j ] = s u m [ i ] [ j − 1 ] + s u m [ a n c [ i ] [ j − 1 ] ] [ j − 1 ] ) sum[i][j]=sum[i][j-1]+sum[anc[i][j-1]][j-1]) sum[i][j]=sum[i][j−1]+sum[anc[i][j−1]][j−1])
这才是树上倍增的真正意义所在,像 R M Q RMQ RMQ求 L C A LCA LCA,是无法解决这类问题的
至此树上倍增讲的差不多了,看例题
例题1:【JZOJ1738】Heatwave
problem
Description 给你N个点的无向连通图,图中有M条边,第j条边的长度为: d_j. 现在有 K个询问。 每个询问的格式是:A
B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?Input
文件名为heatwave.in 第一行: N, M, K。 第2…M+1行: 三个正整数:X, Y, and D (1 <=
X <=N; 1 <= Y <= N). 表示X与Y之间有一条长度为D的边。 第M+2…M+K+1行: 每行两个整数A
B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?Output
对每个询问,输出最长的边最小值是多少。
Sample Input
6 6 8 1 2 5 2 3 4 3 4 3 1 4 8 2 5 7 4 6 2 1 2 1 3 1 4 2 3 2 4 5 1 6 2
6 1Sample Output
5 5 5 4 4 7 4 5
Data Constraint
50% 1<=N,M<=3000 其中30% K<=5000 100% 1 <= N <= 15,000 1 <= M <=
30,000 1 <= d_j <= 1,000,000,000 1 <= K <= 20,000Hint
think about other issues
先不考虑其他的,先考虑一下如何搞定题目所给的问题
注意这句话——
从A点走到B点的所有路径中,最长的边的最小值是多少?
想到什么了吗?
- MST! 既然让最长的边最短,那么我们就求这棵树的最小生成树即可
这样就可以保证两点间最长边最短 ,这里直接用kruskal+并查集艹过去就行了
用邻接表存下即可
analysis
-
求完 M S T MST MST后,这道题是不是就是道裸题?维护 a n c [ i ] [ j ] anc[i][j] anc[i][j]和 d i s [ i ] [ j ] dis[i][j] dis[i][j]即可
照样用一个 d f s dfs dfs遍历整棵树,维护出 d e p t h [ x ] depth[x] depth[x]、 a n c [ x ] [ 0 ] anc[x][0] anc[x][0]和 d i s [ x ] [ 0 ] dis[x][0] dis[x][0],之后 O ( n log 2 n ) O(n\log_2n) O(nlog2n)预处理 -
搞定之后,我们对每一对 ( u , v ) (u,v) (u,v)求 L C A LCA LCA(设 u u u深度更深)注意求 L C A LCA LCA过程中记录每一次的max值即
a n s = m a x ( d i s u , k ) ans=max(dis_{u,k}) ans=max(disu,k) -
a n s ans ans即为答案
时间复杂度为 O ( m l o g 2 m + n l o g 2 n + q l o g 2 n ) O(mlog_2m+nlog_2n+qlog_2n) O(mlog2m+nlog2n+qlog2n)我乱算的
code
var b,c,next,last,father,depth:array[0..50000]of longint; anc,dis:array[0..15000,0..16]of longint; a:array[0..30000,0..3]of longint; n,m,q,i,j,x,y,tot:longint; procedure swap(var x,y:longint); var z:longint; begin z:=x; x:=y; y:=z; end; function max(x,y:longint):longint; begin if x>y then exit(x); exit(y); end; procedure qsort(l,r:longint); var i,j,mid:longint; begin i:=l; j:=r; mid:=a[(l+r)div 2,3]; repeat while a[i,3]<mid do inc(i); while a[j,3]>mid do dec(j); if i<=j then begin a[0]:=a[i]; a[i]:=a[j]; a[j]:=a[0]; inc(i); dec(j); end; until i>j; if l<j then qsort(l,j); if i<r then qsort(i,r); end; function getfather(x:longint):longint; begin if father[x]=x then exit(x); father[x]:=getfather(father[x]); exit(father[x]); end; function judge(x,y:longint):boolean; begin exit(getfather(x)=getfather(y)); end; procedure insert(x,y,z:longint); begin inc(tot); b[tot]:=y; next[tot]:=last[x]; last[x]:=tot; c[tot]:=z; end; procedure dfs(x,y:longint); var now:longint; begin now:=last[x]; while now<>0 do begin if b[now]<>y then begin anc[b[now],0]:=x; depth[b[now]]:=depth[x]+1; dis[b[now],0]:=c[now]; dfs(b[now],x); end; now:=next[now]; end; end; function lca(x,y:longint):longint; var k:longint; begin lca:=0; if depth[x]<depth[y] then swap(x,y); k:=trunc(ln(depth[x]-depth[y]+1)/ln(2)); while k>=0 do begin if depth[anc[x,k]]>depth[y] then begin lca:=max(lca,dis[x,k]); x:=anc[x,k]; end; dec(k); end; if depth[x]<>depth[y] then begin lca:=max(lca,dis[x,0]); x:=anc[x,0]; end; k:=trunc(ln(depth[x])/ln(2)); while k>=0 do begin if anc[x,k]<>anc[y,k] then begin lca:=max(max(lca,dis[x,k]),dis[y,k]); x:=anc[x,k]; y:=anc[y,k]; end; dec(k); end; if x=y then exit(lca); exit(max(lca,max(dis[x,0],dis[y,0]))); end; begin readln(n,m,q); for i:=1 to n do father[i]:=i; for i:=1 to m do readln(a[i,1],a[i,2],a[i,3]); qsort(1,m); for i:=1 to m do begin if (not judge(a[i,1],a[i,2])) then begin insert(a[i,1],a[i,2],a[i,3]); insert(a[i,2],a[i,1],a[i,3]); father[getfather(a[i,1])]:=getfather(a[i,2]); end; end; depth[1]:=1; dfs(1,0); for j:=1 to trunc(ln(n)/ln(2)) do for i:=1 to n do begin anc[i,j]:=anc[anc[i,j-1],j-1]; dis[i,j]:=max(dis[i,j-1],dis[anc[i,j-1],j-1]); end; for i:=1 to q do begin readln(x,y); writeln(lca(x,y)); end; end.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
例题2:【JZOJ2753】树(tree)
problem
Description
在这个问题中,给定一个值S和一棵树。在树的每个节点有一个正整数,问有多少条路径的节点总和达到S。路径中节点的深度必须是升序的。假设节点1是根节点,根的深度是0,它的儿子节点的深度为1。路径不必一定从根节点开始。
- 1
Input
第一行是两个整数N和S,其中N是树的节点数。 第二行是N个正整数,第i个整数表示节点i的正整数。 接下来的N-1行每行是2个整数x和y,表示y是x的儿子。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
Output
输出路径节点总和为S的路径数量。
- 1
Sample Input
3 3 1 2 3 1 2 1 3
Sample Output
2
Data Constraint
Hint
对于30%数据,N≤100;
对于60%数据,N≤1000;
对于100%数据,N≤100000,所有权值以及S都不超过1000。
analysis
相信这题应该难不住你了吧
正解即为树上倍增+二分
首先还是一样,用 O ( n log 2 n ) O(n\log_2n) O(nlog2n)的时间预处理 a n c anc anc数组
至于权值,你可以顺便维护 d i s dis dis数组,但为何不用简单的前缀和呢?
剩下来的就比较简单啦
-
枚举节点 i i i,二分一个 m i d mid mid表示 i i i的第 m i d mid mid个祖先
-
然后通过 a n c anc anc数组用 O ( log 2 n ) O(\log_2n) O(log2n)的时间求出 i i i的第 m i d mid mid个祖先是哪个节点 (设为是第 k k k号)
-
若 p r e [ i ] − p r e [ k ] > s pre[i]-pre[k]>s pre[i]−pre[k]>s则 r i g h t = m i d − 1 right=mid-1 right=mid−1, p r e [ i ] − p r e [ k ] < s pre[i]-pre[k]<s pre[i]−pre[k]<s则 l e f t = m i d + 1 left=mid+1 left=mid+1
= s =s =s就刚好找到了 -
此时累加答案即可
时间复杂度为 O ( n log 2 2 n ) O(n\log^2_2n) O(nlog22n)
code
#include<bits/stdc++.h> #define MAXN 100001 using namespace std; int last[MAXN],next[MAXN],tov[MAXN]; int a[MAXN],value[MAXN],depth[MAXN]; int f[MAXN][21]; int n,s,tot,ans; void insert(int x,int y) { next[++tot]=last[x]; last[x]=tot; tov[tot]=y; } void dfs(int x) { for (int i=last[x];i;i=next[i]) { int j=tov[i]; value[j]=value[x]+a[j]; f[j][0]=x; depth[j]=depth[x]+1; dfs(j); } } int find(int x,int k) { int t=0; while (k) {
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38