【深度学习】梯度下降（通俗易懂）_深度学习梯度下降

文章目录

1、前言

2、理论与代码

1、求极值问题

2、梯度下降

3、实例演示

---

1、前言

最近有朋友问到我，损失函数与激活函数的问题，由于工作等原因有段时间没接触深度学习没有回答的很好。我最近也是浅浅复习了下深度学习，正好分享下自己对深度学习的理解。

2、理论与代码

1、求极值问题

大家可以思考下， y =(x-3)**2+1 ，y的最小值怎么求的。这里常规做法应该是：

1、因为(x-3)**2>=0 所以y>=1 所以最小值1

2、对x求导，令 dy/dx = 2(x-3)  等于0 ，求导x=3 极值点，根据导数判断当x<3，dy/dx <0，递减，x>3，dy/dx>0递增。带入原方程算得极小值为1，简单判断下，这个极小值就是最小值。

3、来看看我们利用梯度下降的思想如何做（导数与梯度是不同的，一个标量一个矢量。为了便于说明，我们后面直接说梯度）

先观察下函数图像。

给个任意初始值x，如 x = -1，我们想要找到x = 3，如何做呢。根据导数dy/dx，我们可以对x迭代。x = x - dy/dx ，由于我们 dy/dx 计算的值比较大，就相当于我们每次迭代 x 一步跨的很长。所以我们设定一个参数 lr （learning rate）也就是我们所说的"学习率"或者"步长"。

  x = x-lr*dy/dx 

我们写段代码看下。

import matplotlib.pyplot as plt
import numpy as np
 
# 先画下 y = (x-3)**2 + 1 曲线图
m = np.linspace(-1,7,1000)
n = m**2 - 6*m + 10
plt.plot(m,n)
 
x = -1    # 给个x的初始值
lr = 0.01    # 学习率
list_x,list_y= [],[] 
 
for epoch in range(200):  
    y_d = 2*x - 6    # y对x的导数 y_d
    list_x.append(x)
    list_y.append(x**2 - 6*x + 10)    # 把每次的数据存下，后面可视化
    x = x - y_d*lr
 
# 每次迭代散点图     
plt.scatter(list_x,list_y,color="red")
plt.show()

1、可以发现，我们在迭代过程中，逐渐接近我们想要的值。迭代的这个过程x = x-lr*dy/dx 是极其关键。我们可以理解为  往下走楼梯，一步一步逐渐接近于我们的目标。

2、当我们要求极大值时，比如求 - (x-3)**2+1 的极大值，我们只需要上述式子 负号变为正号就可以了 x = x + lr*dy/dx ，这个过程 我们称为 梯度上升。我们平常讲的都是梯度下降，因为我们要的就是求最小值。我们要建立的模型是 y = F(x)，要求模型输出的值越接近实际值，也就是误差（损失）最小。后面会举个实例说明。

3、大家可以自行调整上述代码的两个参数 lr 、 迭代次数。

比如 我现在设置  lr = 1.0 ，会发现什么？无论迭代次数是多少，总会在两个点来回震荡。

关于参数这个就不过多说明了，大家可以自己实践下。

2、梯度下降

梯度这个概念相信大家都知道，不记得的可以百度看下。

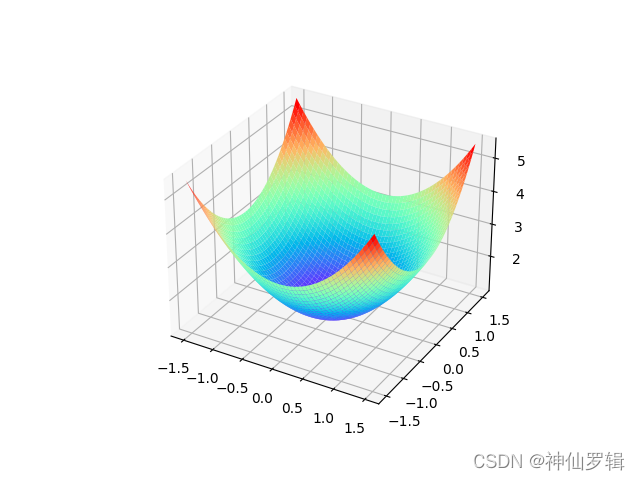
举个例子：求 z = x**2 + y**2 + 1 最小值  ，把导数换成各个参数的偏导，其他类似。直接上代码 

import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
 
 
# 计算z = x**2+ y**2 + 1 的最小值
'''
可视化3D图
'''
fig = plt.figure()
ax1 = plt.axes(projection="3d")
x = np.linspace(-1.5,1.5,1000)
y = np.linspace(-1.5,1.5,1000)
x,y = np.meshgrid(x,y)
z = x**2 + y**2 + 1
ax1.plot_surface(x,y,z,cmap="rainbow")
plt.show()
 
x,y = -2,-2   # 随机给个初始值
lr = 0.02    # 学习率
 
for i in range(100):
    z_x = 2*x    # z对x偏导
    z_y = 2*y    # z对y偏导
    x = x-z_x*lr
    y = y-z_y*lr
    print(x,y)    # 打印看下发现(x,y)越来越接近(0,0)

3、实例演示

还是来个例子演示一遍

特征1数据 ： x_data = [1,2,3,4,5]

特征2数据 ： y_data = [6,5,4,3,2]

结果：result = [12,9,6,3,0]

现用梯度下降思想来演示一下。

假设 用方程 z = w1*x + w2*y + b 去拟合

def linear_function(x, y):
    return w1 * x + w2 * y + b
 
 
"""
定义一个误差函数，比如绝对值损失，均方损失，交叉熵损失。
实际上我们定义的这个my_loss就是均方误差，也就是我们所说的MSE。
"""
def my_loss(x, y, z):
    loss = 0
    n = len(x)  # n代表数据组数
    for xi, yi, zi in zip(x, y, z):
        z_pred = linear_function(xi, yi)
        loss += (z_pred - zi) ** 2 / n  # 平方和平均
    return loss
 
 
# 定义个梯度函数
def my_gradient(x, y, z):
    n = len(x)  # 多少组数
    a, b, c = 0, 0, 0
    for xi, yi, zi in zip(x, y, z):
        z_pred = linear_function(xi, yi)
        """
        现在目标是求损失值最小，我们定义的损失为(z-(w1*x + w2*y + b))**2/n
        问题是我们在求解每组数据都会有一个梯度，如何处理呢。简单介绍三种做法。
        我们这里用的第一种
        1、对每一组梯度进行一个求和，就是我们所说的批量梯度下降，所有组的梯度累加。
        特点：全局最优，但是速度慢。
        2、随机梯度下降，每组数据单独算梯度。每组数据单独计算。
        特点：每个参数迭代速度快，但是容易陷局部最优
        3、小批量梯度下降，选取一部分组梯度下降。比如我们这里截取前几组数据。
        """
        a += 2 * xi * (z_pred - zi) / n
        b += 2 * yi * (z_pred - zi) / n
        c += 2 * (z_pred - zi) / n
    return a, b, c
 
 
if __name__ == "__main__":
    w1, w2, b = 0, 0, 0  # 随机给初始值
    x_data = [1, 2, 3, 4, 5]
    y_data = [6, 5, 4, 3, 2]
    result = [12, 9, 6, 3, 0]
    ls = 0.01  # 学习率
    for epoch in range(500):
        loss = my_loss(x_data, y_data, result)  # 记录损失值
        grad = my_gradient(x_data, y_data, result)
        # 批量梯度下降，每次更新每个参数
        w1 -= ls * grad[0]
        w2 -= ls * grad[1]
        b -= ls * grad[2]
        print("epoch={},loss={}".format(epoch, loss))
    print("result", result)
    # 打印看下我们求得的结果值与目标值
    for x, y in zip(x_data, y_data):
        print(w1 * x + w2 * y + b, end=" ")
 
"""
epoch=496,loss=9.387598846525591e-30
epoch=497,loss=9.387598846525591e-30
epoch=498,loss=9.387598846525591e-30
epoch=499,loss=9.387598846525591e-30
result [12, 9, 6, 3, 0]
11.999999999999995 8.999999999999998 5.999999999999999 3.0000000000000013 3.58046925441613e-15 
"""

看的出来，效果挺好的。这里又会有个新的问题。

我们怎么知道它是 z = w1*x + w2*y + b ，或者说我们为什么这样假设呢？如果我假设是多次呢？

这就是交给我们的神经网络了。假设我不是线性的呢，这就跟我们激活函数有关了。这次分享的东西可谓是冰山一角中的一角的。。。突然想到校训"求索"。路漫漫其修远兮，吾将上下而求索。

祝大家假期愉快！