HashMap与红黑树_hashmap红黑树

作者：小蓝xlanll | 2024-04-21 11:21:02

踩

hashmap红黑树

一、为什么需要HashMap?

在我们写程序的时候经常会遇到数据检索等操作，对于几百个数据的小程序而言，数据的存储方式或是检索策略没有太大影响，但对于大数据，效率就会差很远。

1、线性检索：

线性检索是最为直白的方法，把所有数据都遍历一遍，然后找到你所需要的数据。其对应的数据结构就是数组，链表等线性结构，这种方式对于大数据而言效率极低，其时间复杂度为O(n)。

2、二分搜索：

二分搜索算是对线性搜索的一个改进，比如说对于[1，2，3，4，5，6，7，8]，我要搜索一个数（假设是2），我先将这个数与4（这个数一般选中位数比较好）比较，小于4则在4的左边[1，2，3]中查找，再与2比较，相等，就成功找到了，这种检索方式好处在于可以省去很多不必要的检索，每次只用查找集合中一半的元素。其时间复杂度为O(logn)。但其也有限制，数排列本身就需要是有序的。

3、Hash表中的查找：

好了，重点来了，Hash表闪亮登场，这是一种时间复杂度为O(1)的检索，就是说不管你数据有多少只需要查一次就可以找到目标数据。大家请看下图。

大家可以看到这个数组中的值就等于其下标，比如说我要存11，我就把它存在a[11]里面，这样我要找某个数字的时候就直接对应其下标就可以了。这其实是一种牺牲空间换时间的方法，这样会对内存占用比较大，但检索速度极快，只需要搜索一次就能查到目标数据。

看了上面的Hash表你肯定想问，如果我只存一个数10000，那我不是要存在a[10000]，这样其他空间不是白白浪废了吗，好吧，不存在的。Hash表已经有了其应对方法，那就是Hash函数。Hash表的本质在于可以通过value本身的特征定位到查找集合的元素下标，从而快速查找。一般的Hash函数为：要存入的数 mod（求余） Hash数组长度。比如说对于上面那个长度为9的数组，12的位置为12 mod 9=3，即存在a3，通过这种方式就可以安放比较大的数据了。

4、Hash冲突解决策略

看了上面的讲解，有出现了一个问题，通过求余数得到的地址可能是一样的。这种我们称为Hash冲突，如果数据量比较大而Hash桶比较小，这种冲突就很严重。我们采取如下方式解决冲突问题。

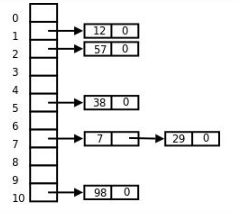
我们可以看到12和0的位置冲突了，然后我们把该数组的每一个元素变成了一个链表头，冲突的元素放在了链表中，这样在找到对应的链表头之后会顺着链表找下去，至于为什么采用链表，是为了节省空间，链表在内存中并不是连续存储，所以我们可以更充分地使用内存。

上面讲了那么多，那跟我们今天的主题HashMap有什么关系呢？进入正题。我们知道HashMap中的值都是key，value，这里的存储与上面的很像，key会被映射成数据所在的地址，而value就在以这个地址为头的链表中，这种数据结构在获取的时候就很快。

但是又出现了一个问题：如果hash桶较小，数据量较大，就会导致链表非常的长。所以就出现了红黑树。

二、红黑树的出现

在JDK1.6，JDK1.7中，HashMap采用位桶+链表实现，即使用链表处理冲突，同一hash值的链表都存储在一个链表里。但是当位于一个桶中的元素较多，即hash值相等的元素较多时，通过key值依次查找的效率较低。而JDK1.8中，HashMap采用位桶+链表+红黑树实现，当链表长度超过阈值（8）时，将链表转换为红黑树，这样大大减少了查找时间。在jdk1.8版本后，java对HashMap做了改进，在链表长度大于8的时候，将后面的数据存在红黑树中，以加快检索速度。

JDK1.8HashMap的红黑树是这样解决的：

如果某个桶中的记录过大的话（当前是TREEIFY_THRESHOLD = 8），HashMap会动态的使用一个专门的treemap实现来替换掉它。这样做的结果会更好，是O(logn)，而不是糟糕的O(n)。

它是如何工作的？前面产生冲突的那些KEY对应的记录只是简单的追加到一个链表后面，这些记录只能通过遍历来进行查找。但是超过这个阈值后HashMap开始将列表升级成一个二叉树，使用哈希值作为树的分支变量，如果两个哈希值不等，但指向同一个桶的话，较大的那个会插入到右子树里。如果哈希值相等，HashMap希望key值最好是实现了Comparable接口的，这样它可以按照顺序来进行插入。这对HashMap的key来说并不是必须的，不过如果实现了当然最好。如果没有实现这个接口，在出现严重的哈希碰撞的时候，你就并别指望能获得性能提升了。

三、实现原理

HashMap可以看成是一个大的数组，然后每个数组元素的类型是Node类。当添加一个元素（key-value）时，就首先计算元素key的hash值，以此确定插入数组中的位置，但是可能存在同一hash值的元素已经被放在数组同一位置了，这时就添加到同一hash值的元素的后面，他们在数组的同一位置，但是形成了链表，同一各链表上的Hash值是相同的，所以说数组存放的是链表。而当链表长度太长时，链表就转换为红黑树，这样大大提高了查找的效率。

当链表数组的容量超过初始容量的0.75时，再散列将链表数组扩大2倍，把原链表数组的搬移到新的数组中。

四、数据结构

上面说过HashMap可以看成是一个大的数组，然后每个数组元素的类型是Node类型，源码里定义如下：

transient Node<K,V>[] table;

注意Node类还有两个子类：TreeNode和Entry

TreeNode <K,V> extends Entry<K,V> extends Node<K,V>

上图中的链表就是Node类，而红黑树正是TreeNode类。

HashMap存取put/get


//对外开发使用
public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}
//存值的真正执行者
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
    
    //定义一个数组，一个链表，n永远存放数组长度，i用于存放key的hash计算后的值，即key在数组中的索引        
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    
    //判断table是否为空或数组长度为0，如果为空则通过resize()实例化一个数组并让tab作为其引用，并且让n等于实例化tab后的长度        
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;
    
    //根据key经过hash()方法得到的hash值与数组最大索引做与运算得到当前key所在的索引值，并且将当前索引上的Node赋予给p并判断是否该Node是否存在
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);//若tab[i]不存在，则直接将key-value插入该位置上。
    
        //该位置存在数据的情况  
    else {
        Node<K,V> e; K k; //重新定义一个Node，和一个k
        
	    // 该位置上数据Key计算后的hash等于要存放的Key计算后的hash并且该位置上的Key等于要存放的Key     
        if (p.hash == hash &&((k = p.key) == key || (key != null && key.equals(k))))
            e = p;	//true，将该位置的Node赋予给e
	else if (p instanceof TreeNode)  //判断当前桶类型是否是TreeNode
	    //ture，进行红黑树插值法,写入数据
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); 	
        else {	
	    //false, 遍历当前位置链表
            for (int binCount = 0; ; ++binCount) {
                //查找当前位置链表上的表尾，表尾的next节点必然为null,找到表尾将数据赋给下一个节点
                if ((e = p.next) == null) {
                     p.next = newNode(hash, key, value, null);	//是，直接将数据写到下个节点
                    // 如果此时已经到第八个了，还没找个表尾，那么从第八个开始就要进行红黑树操作
		    if (binCount >= TREEIFY_THRESHOLD - 1)
                        treeifyBin(tab, hash);	//红黑树插值具体操作
                        break;
                }
                //如果当前位置的key与要存放的key的相同，直接跳出，不做任何操作   
                if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                //将下一个给到p进行逐个查找节点为空的Node
		p = e;
            }
        }
        //如果e不为空，即找到了一个去存储Key-value的Node 
	if (e != null) { // existing mapping for key
            V oldValue = e.value;    
	    if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e);
            return oldValue;
        }
    }
    ++modCount;
    //当最后一次调整之后Size大于了临界值，需要调整数组的容量
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    return null;
}

取值：get(key)方法时获取key的hash值，计算hash&(n-1)得到在链表数组中的位置first=tab[hash&(n-1)],先判断first的key是否与参数key相等，不等就遍历后面的链表找到相同的key值返回对应的Value值即可


//对外公开方法
public V get(Object key) {
        Node<K,V> e;
        return (e = getNode(hash(key), key)) == null ? null : e.value;
    }
 
//实际逻辑控制方法
final Node<K,V> getNode(int hash, Object key) {
	//定义相关变量
    Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
	//保证Map中的数组不为空，并且存储的有值，并且查找的key对应的索引位置上有值
    if ((tab = table) != null && (n = tab.length) > 0 && (first = tab[(n - 1) & hash]) != null) {
        // always check first node 第一次就找到了对应的值
	if (first.hash == hash && ((k = first.key) == key || (key != null && key.equals(k))))
            return first;
	//判断下一个节点是否存在
	if ((e = first.next) != null) {
            //true,检测是否是TreeNode
            if (first instanceof TreeNode)
                return ((TreeNode<K,V>)first).getTreeNode(hash, key); //通过TreeNode的get方法获取值
            //否，遍历链表
	    do {
		//判断下一个节点是否是要查找的对象
                if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            }while ((e = e.next) != null);
        }
    }//未找到，返回null
    return null;
 }

扩容


final Node<K,V>[] resize() {
    Node<K,V>[] oldTab = table;
    int oldCap = (oldTab == null) ? 0 : oldTab.length;	//未扩容时数组的容量
    int oldThr = threshold;
    int newCap, newThr = 0;//定义新的容量和临界值
    //当前Map容量大于零，非第一次put值
    if (oldCap > 0) {
        if (oldCap >= MAXIMUM_CAPACITY) {	//超过最大容量:2^30
			//临界值等于Integer类型的最大值 0x7fffffff=2^31-1
            threshold = Integer.MAX_VALUE;	
            return oldTab;
        }
		//当前容量在默认值和最大值的一半之间
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && oldCap >= DEFAULT_INITIAL_CAPACITY)
            newThr = oldThr << 1;	//新临界值为当前临界值的两倍
    }
	//当前容量为0，但是当前临界值不为0，让新的容量等于当前临界值
    else if (oldThr > 0) 
        newCap = oldThr;
    //当前容量和临界值都为0,让新的容量为默认值，临界值=初始容量*默认加载因子
	else {
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
	//如果新的临界值为0
    if (newThr == 0) {
        float ft = (float)newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ? (int)ft : Integer.MAX_VALUE);
    }
	//临界值赋值
    threshold = newThr;
    //扩容table
    Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
    table = newTab;
    if (oldTab != null) {
        for (int j = 0; j < oldCap; ++j) {
            Node<K,V> e;
            if ((e = oldTab[j]) != null) {
                oldTab[j] = null;
                if (e.next == null)
                    newTab[e.hash & (newCap - 1)] = e;//此时newCap = oldCap*2
                else if (e instanceof TreeNode) //节点为红黑树，进行切割操作
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                else { //链表的下一个节点还有值，但节点位置又没有超过8
                    //lo就是扩容后仍然在原地的元素链表
					//hi就是扩容后下标为  原位置+原容量  的元素链表，从而不需要重新计算hash。
					Node<K,V> loHead = null, loTail = null;
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                    //循环链表直到链表末再无节点
					do {
                        next = e.next;
						//e.hash&oldCap == 0 判断元素位置是否还在原位置
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        else {
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
					//循环链表结束，通过判断loTail是否为空来拷贝整个链表到扩容后table
                    if (loTail != null) {
                       loTail.next = null;
                        newTab[j] = loHead;
                    }
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    return newTab;
}

HashMap put与resize的实例图

五、为什么是红黑树？为什么不直接采用红黑树还要用链表？

1、因为红黑树需要进行左旋，右旋操作，而单链表不需要，
如果元素小于8个，查询成本高，新增成本低
如果元素大于8个，查询成本低，新增成本高

2、参考：AVL树和红黑树之间有什么区别？

借鉴博客：https://blog.csdn.net/goosson/article/details/81029729

https://www.cnblogs.com/little-fly/p/7344285.html

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/小蓝xlanll/article/detail/462717