推荐系统中的常用算法——Wide & Deep_产品推荐中deep

1. 概述

在前DeepLearning时代，以Logistic Regression（LR）为代表的广义线性模型在CTR，CVR中得到了广泛的应用，主要原因包括：

1. 模型足够简单，相当于不包括隐含层的神经网络；
2. 可扩展性强；
3. 可解释性强，因为是线性的模型，可以很方便的显现出特征对最终结果的强弱。

虽然线性模型有如上的优点，但同时也存在很多的不足，其中最重要的是无法处理特征的交叉，泛化能力较差。在以CTR为代表的Ranking问题中，需要同时获得记忆（memorization）和泛化（generalization）的能力。记忆可以理解为从历史数据中学习到item或者特征之间的共现关系，泛化则是对上述共现关系的传递，能够对未出现的关系对之间的共现关系进行判定。引用文中的例子：假设样本中包含了共现关系AND(user_installed_app=netflix, impression_app=pandora)表示用户安装了Netflix，并随后见到Pandora（注：美国流媒体音乐）时值为$1$，通过记忆的学习生成特征AND(user_installed_app=netflix, impression_app=pandora)与目标值$1$之间的关系。但是当出现一条样本AND(user_installed_app=哔哩哔哩, impression_app=网易云音乐)，单纯依靠记忆能力就无法做出置信的判断。

为了能够使得线性模型具有特征交叉的能力，人们不得不在特征工程上花费大量的时间。对于广义线性模型来说，也不是解决不了上述的问题，通过特征工程，需要能够挖掘出共现关系AND(user_installed_category=video, impression_category=music)。随着算法的不断发展，随后也出现了许多的优化方案，如FM算法通过在线性模型的基础上引入交叉项，GBDT+LR算法通过GBDT模型对特征的学习，有效的处理特征交叉问题。随着深度学习的发展，深度学习天生的泛化能力，使得人们能够从繁重的特征工程中解放出来。

既然LR模型具有记忆能力，DNN模型具有泛化能力，综合这两部分的能力便能更好的求解Ranking问题。Wide & Deep模型同时具备了这两种能力，LR模型构成了Wide侧，DNN模型构成了Deep侧。

2. Wide & Deep模型

2.1. Wide & Deep模型结构

Wide & Deep模型的结构如下图所示：

在Wide & Deep模型中包括两个部分，分别为Wide部分和Deep部分，Wide部分如上图中的最左侧的图（Wide Models）所示，Deep部分如上图中的最右侧的图（Deep Models）所示。

2.1.1. Wide侧模型

Wide侧模型就是一个广义的线性模型，如下图所示：

Wide侧的广义线性模型可以表示为：

$$y={\mathbf{w}}^T\mathbf{x}+b$$

其中，特征$\mathbf{x}=\left[x_1,x_2,\cdots ,x_d\right]$是一个$d$维的向量，$\mathbf{w}=\left[w_1,w_2,\cdots ,w_d\right]$为模型的参数。最终在$y$的基础上增加Sigmoid函数作为最终的输出。对于广义线性模型的特征$\mathbf{x}$，通常需要特征工程的参与，特征中不仅包含了原始的特征，还包括一些交叉特征，如上述的AND(user_installed_app=netflix, impression_app=pandora)特征。

2.1.2. Deep侧模型

Deep侧模型是一个典型的DNN模型，如下图所示：

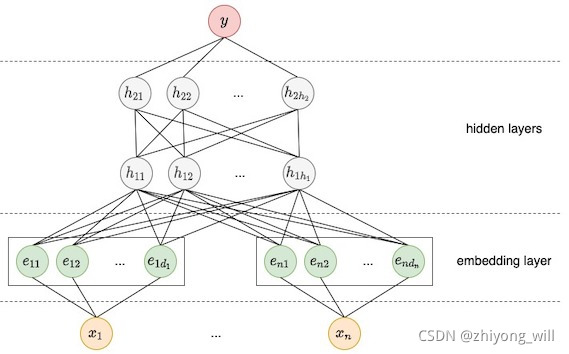
对于DNN模型来说，不适合处理离散的稀疏特征，因此在深度神经网络模型中，通常需要将输入的离散稀疏特征转换成连续的稠密特征，如上图中的embedding层。在训练的时候，模型中的embedding向量参与模型一起运算。隐含层的计算方法为：

$$a^{\left(l+1\right)}=f\left(W^{\left(l\right)}{a}^{(l)}+b^{\left(l\right)}\right)$$

其中，$f$称为激活函数，如ReLUs。$a^{(l)}$表示的是第$l$层的激活函数输出，$b^{\left(l\right)}$表示的是第$l$层的偏置，$W^{\left(l\right)}$表示的是第$l$层的模型权重。

2.2. Wide & Deep模型的联合训练（joint training）

联合训练是指同时训练Wide侧模型和Deep侧模型，并将两个模型的结果的加权和作为最终的预测结果：

$$P\left(Y=1\mid \mathbf{x}\right)=\sigma \left({\mathbf{w}}_{wide}^T\left[\mathbf{x},\varphi \left(\mathbf{x}\right)\right]+{\mathbf{w}}_{deep}^T{a}^{\left(l_f\right)}+b\right)$$

其中，$\mathbf{x}$表示的wide侧的原始特征，$\varphi \left(\mathbf{x}\right)$表示的是经过特征工程后的交叉特征。

原文中提到模型训练采用的是联合训练（joint training），模型的训练误差会同时反馈到Wide侧模型和Deep侧模型中进行参数更新。Joint training与ensemble learning是不同的，对于ensemble learning来说，模型之间是相互独立的，每一个模型独立训练，仅在做inference的时候做最终结果的融合；而对于joint training来说，多个模型是一起训练的，最终的结果受到各个模型的相互影响，如Wide & Deep中最终的结果受到Wide侧模型和Deep侧模型的共同影响，因此在Wide & Deep中，Wide侧模型需要侧重于memorization的训练，而Deep侧模型需要侧重于generalization的训练，从而使得单个模型的大小和复杂度能得到控制。

对于上述问题的损失函数为

$$L=-\frac{1}{N}\sum _{\left(\hat{y},y\right)\in \mathbb{D}}\left(ylog\hat{y}+\left(1-y\right)log\left(1-\hat{y}\right)\right)$$

其中，$y$为真实的标签，$\hat{y}$为预测值，即$\hat{y}=P\left(Y=1\mid \mathbf{x}\right)$。Wide & Deep模型中的参数为${\mathbf{w}}_{wide}^T$，${\mathbf{w}}_{deep}^T$和$b$。

在Tensorflow的1.x版本中提供了如下的Wide & Deep函数:

tf.estimator.DNNLinearCombinedClassifier(
    model_dir=None, linear_feature_columns=None, linear_optimizer='Ftrl',
    dnn_feature_columns=None, dnn_optimizer='Adagrad', dnn_hidden_units=None,
    dnn_activation_fn=tf.nn.relu, dnn_dropout=None, n_classes=2, weight_column=None,
    label_vocabulary=None, input_layer_partitioner=None, config=None,
    warm_start_from=None, loss_reduction=losses.Reduction.SUM, batch_norm=False,
    linear_sparse_combiner='sum'
)
1
2
3
4
5
6
7
8

文中提到针对Wide侧和Deep采用不同的训练方法，如Wide侧模型采用FTRL（设置上述函数中的linear_optimizer参数），Deep侧模型：AdaGrad

2.3. 特征处理

通过对Wide & Deep模型的分析，Wide & Deep模型本身并不复杂。如上所述，Wide侧模型需要侧重于memorization的训练，而Deep侧模型需要侧重于generalization的训练，因此在实际的应用中，应针对不同的业务场景，对Wide & Deep的Wide侧和Deep侧选择不同的特征，充分发挥Wide & Deep模型的优势。文中将Wide & Deep模型应用在Google play的apps推荐中。

模型的训练之前，最重要的工作是训练数据的准备以及特征的选择，在apps推荐中，可以使用到的数据包括用户和曝光数据。因此，每一条样本对应了一条曝光数据，同时，样本的标签为$1$表示安装，$0$则表示未安装。对于每条样本中特征的选择，可以参见下图：

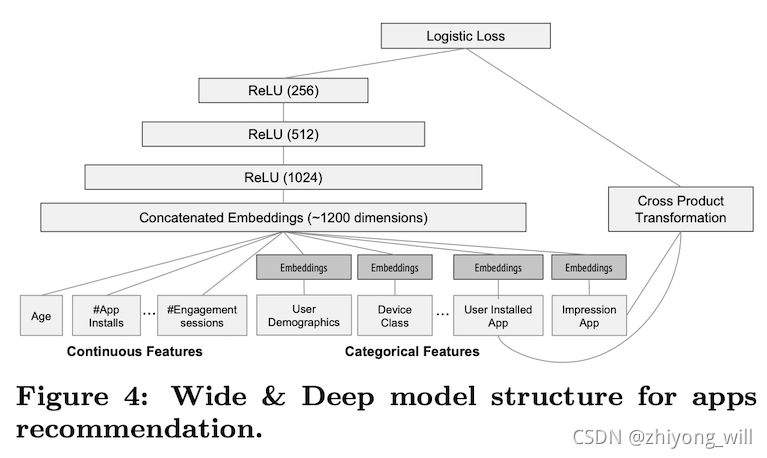
对于特征的选择，从上图中可以看出：

• Wide侧主要是User Installed App和Impression App的交叉特征，用于记忆用户的兴趣
• Deep侧的特征包括连续特征和类别特征：
  • 连续特征，通过归一化到区间$\left[0,1\right]$后直接输入到DNN中
  • 类别特征，通过词典（Vocabularies）将其映射成32维的稠密向量。

对于具体的特征的选择，一般包括用户侧的静态特征，如年龄，性别等，用户侧的行为特征，如历史点击（如本文中的历史安装），还包括一些上下文的特征，如session的特征，特征的选择没有固定的套路，需要根据具体的场景做合适的选择。

参考文献

1. Cheng H T, Koc L, Harmsen J, et al. Wide & Deep Learning for Recommender Systems[J]. 2016:7-10.
2. wide & Deep 和 Deep & Cross 及tensorflow实现
3. Wide & Deep 的官方实现
4. 深度学习在 CTR 中应用
5. 《Wide & Deep Learning for Recommender Systems 》笔记
6. 深度学习在美团点评推荐平台排序中的运用
7. [tensorflow线性模型以及Wide deep learning