数据结构-二叉树-堆（二）

一、建堆的时间复杂度问题

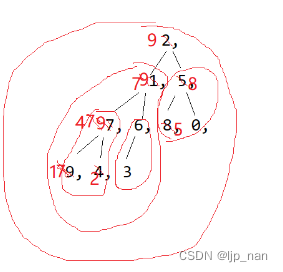
1、除了向上调整建堆，我们还可以向下调整建堆。不能在根上直接开始向下调整。这里的条件就是左右子树必须都是大堆或者小堆。我们可以倒着往前走，可以从最后一个叶子开始调整。但是从叶子开始调整没有意义。所以我们可以从倒数的第一个的非叶子开始调整。也就是最后一个叶子的父亲节点开始向下调整建堆。一层一层向上进行向下调整建堆，把大的数字往上调小的数字往下沉。那么问题来了怎么找到最后一个叶子的父亲节点。

我们先可以求出最后一个孩子的下标然后应用公式 parent = （child-1）/ 2 算出最后一个孩子的父亲节点的下标。

void HeapSort(int* a,int n)
{
	//首先建立大堆
	/*for (int i = 1; i < n; i++)
	{
		UpAdjust(a, i);
	}*/
 
	//向下调整建堆的效率要比向上调整建堆的效率要高
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		DownAdjust(a, i, n);
	}
 
	//交换堆头和堆尾的数字选出最大的数字放到堆尾
	//然后向下调整
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[end], &a[0]);
		DownAdjust(a, 0, end);
		end--;
	}
}

2、向下调整和向上调整建堆的时间复杂度

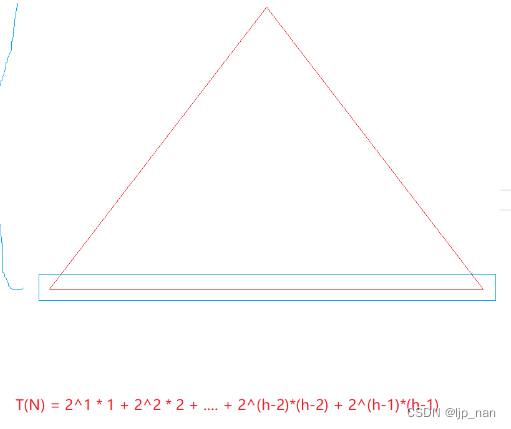
向下调整：倒数第二层有2^(h-2) 个节点

建堆的调整的次数

错位相减法算出时间复杂度

每层节点个数 × 这一层最坏向下调整多少次

最后的结果为：

、

所以时间复杂度为O(N)  T(N) = N - h。

向上调整：

再次使用上面的错位相减法

所以时间复杂度为O(NlogN)。

因为向下调整的过程中节点多的调整的次数少，节点少的调整的次数多。向上调整的过程中节点少的调整的次数少，节点多的调整的次数多

排序调堆的时间复杂度也是O(NlogN)。

TOPK 问题

1、建N个数的大堆，再Pop k次就可以了。

2、加入N很大呢？N是100亿呢？ K == 50

      1G大约十亿字节。所以是40G左右

内存中存不下，数据是在磁盘文件中。

我们可以用100亿个数中的K个数建立一个小堆。遍历剩下的数据，如果这个数据比堆顶的数据大，就替代它进堆（向下调整）最后这个小堆的数据就是最大的前K个。

void HeapTopK(int* a, int n, int k)
{
	//首先向下调整建堆
	int* topk = (int*)malloc(sizeof(int) * k);
	//从a数组里读
	for (int i = 0; i < k; i++)
	{
		topk[i] = a[i];
	}
    //建立小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		DownAdjust(topk, i, k);
	}
	//遍历剩下的数如果大于堆顶的数据我们就让它进堆并向下调整
	for (int i = k + 1; i < n; i++)
	{
		if (a[i]  > topk[0])
		{
			topk[0] = a[i];
			DownAdjust(topk, 0, k);
		}
	}
}