数据结构之完全二叉树

一、完全二叉树定义

完全二叉树(Complete Binary Tree)

若设二叉树的深度为h，除第 h 层外，其它各层 (1~h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

一棵二叉树至多只有最下面的一层上的结点的度数可以小于2，并且最下层上的结点都集中在该层最左边的若干位置上，而在最后一层上，右边的若干结点缺失的二叉树，则此二叉树成为完全二叉树。

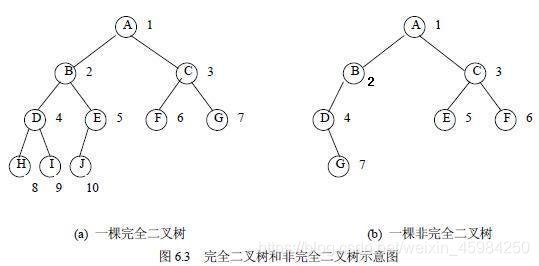
二、完全二叉树特点

1、叶子结点只可能在最大的两层上出现,对任意结点，若其右分支下的子孙最大层次为L，则其左分支下的子孙的最大层次必为L 或 L+1;
2、出于简便起见,完全二叉树通常采用数组而不是链表存储。
3、满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。
4、完全二叉树第i层至多有2^(i-1)个节点，共i层的完全二叉树最多有2^i-1个节点。
5、只允许最后一层有空缺结点且空缺在右边，即叶子结点只能在层次最大的两层上出现；
6、对任一结点，如果其右子树的深度为j，则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个。

三、判断完全二叉树及实现方法

完全二叉树：叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。

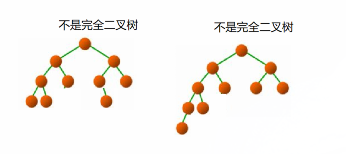
实现方法：
1、针对这个完全二叉树进行层序遍历；
2、判定是不是完全二叉树的时候,需要分成两个阶段来判定：
a)第一阶段,要求每个被访问到的节点,都要有两个子树
如果当前这个节点只有左子树,就需要进入第二阶段了；
如果当前节点没有子树,也是进入第二阶段；
如果当前节点只有右子树,那么直接认为这就不是完全二叉树。
b)第二阶段,要求每个被访问到的节点,必须没有子树。

四、层序遍历

上面描述中出现了层序遍历，现在我们来说一说层序遍历以及它的实现。

1、层序遍历的定义

层序遍历，就是按二叉树从上到下，从左到右依次打印每个节点中存储的数据。如下图：

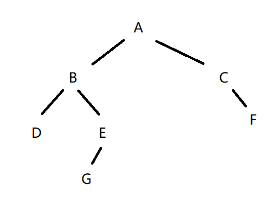
层序遍历：ABCDEFG

2、层序遍历的实现方法

实现层序遍历,需要借助一个“队列”：
1、先把根节点放到队列里；
2、进行出队列操作,并且访问这个节点3，把当前节点的左子树和右子树再入队列(空树就不管了)；
4.回到2继续循环执行.

3、代码实现

public static void levelOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (true) {
            TreeNode cur = queue.poll();
            if (cur == null) {
                break;
            }
            // 访问当前节点. 就用打印表示访问即可.
            System.out.print(cur.val);
            // 把该节点的左子树入队列, 右子树入队列
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

五、判断完全二叉树的代码实现

public static boolean isCompleteTree(TreeNode root) {
        // 通过层序遍历的方式来实现
        if (root == null) {
            return true;
        }
        // 分成两个阶段来进行判定
        // 这个变量为 false, 表示当前是第一阶段,
        // 变量为 true 表示进入第二阶段
        boolean isLevel2 = false;

        // 层序遍历, 需要有一个队列
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (true) {
            TreeNode cur = queue.poll();
            if (cur == null) {
                break;
            }
            // 针对当前节点进行访问.
            // 此处的访问是一系列的逻辑判断
            if (!isLevel2) {
                // 第一阶段的逻辑
                if (cur.left != null && cur.right != null) {
;                   // 这是一个符合要求的节点, 继续往下遍历即可.
                    // 此时直接把左右子树入队列即可
                    queue.offer(cur.left);
                    queue.offer(cur.right);
                } else if (cur.left == null && cur.right != null) {
                    // 第一阶段中发现只有右子树的节点!!
                    // 说明这个树一定不是完全二叉树
                    return false;
                } else if (cur.left != null && cur.right == null) {
                    // 遇到了这个节点不符合第一阶段的条件,
                    // 进入到第二阶段继续判定
                    isLevel2 = true;
                    queue.offer(cur.left);
                } else {
                    // 这个节点没有子树
                    // 也是进入到第二阶段继续判定
                    isLevel2 = true;
                }
            } else {
                // 第二阶段的逻辑
                if (cur.left != null || cur.right != null) {
                    // 发现第二阶段的某个节点的子树不为空, 此时就认为当前不是完全二叉树
                    return false;
                }
            }
        }
        // 遍历了整个树, 也没找到 return false 的反例.
        return true;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53