【论文笔记】Scalable Diffusion Models with State Space Backbone

原文链接：https://arxiv.org/abs/2402.05608

1. 引言

主干网络是扩散模型发展的关键方面，其中基于CNN的U-Net（下采样-跳跃连接-上采样）和基于Transformer的结构（使用自注意力替换采样块）是代表性的例子。

状态空间模型（SSM）在长序列建模方面有极大潜力。本文受Mamba启发，建立基于SSM的扩散模型，称为DiS。DiS将所有输入（时间、条件和有噪声的图像patch）视为离散token。DiS中的状态空间模型使其比CNN和Transformer有更优的放缩性，且有更低的计算开销。

2. 方法

2.1 准备知识

扩散模型：扩散模型逐步向数据加入噪声，然后将此过程反过来从噪声生成数据。噪声的加入过程称为前向过程，可表达为马尔科夫链。逆过程中，使用高斯模型近似真实逆转移，其中学习相当于对噪声的预测（即使用噪声预测网络，来最小化噪声预测目标）。

条件扩散模型会将条件（如类别、文本等，通常形式为索引或连续嵌入）引入噪声预测目标中。

具体公式见扩散模型（Diffusion Model）简介 - CSDN。

状态空间主干：状态空间模型的传统定义是将$x(t)\in {\mathbb{R}}^N$通过隐状态$h(t)\in {\mathbb{R}}^N$映射为$y(t)\in {\mathbb{R}}^N$的线性时不变系统：
$$\begin{gathered} h^{\prime }(t)=Ah(t)+Bx(t) \\ y(t)=Ch(t) \end{gathered}$$

其中$A\in {\mathbb{R}}^{N\times N}$为状态矩阵，$B,C\in {\mathbb{R}}^N$为输入和输出矩阵。真实世界的数据通常为离散形式，可将上式离散化为
$$\begin{gathered} h_t=\bar{A}{h}_{t-1}+\bar{B}{x}_t \\ {y}_t=C{h}_t \end{gathered}$$

其中$\bar{A}=\exp (\Delta \cdot A),\bar{B}=(\Delta \cdot A{)}^{-1}(\exp (\Delta \cdot A)-I)\cdot (\Delta B)$为离散状态参数，$\Delta$为离散步长。

虽然SSM理论上性质优良，但通常有高计算量和数值不稳定性。结构状态空间模型（S4）通过强制$A$的形式来减轻这一问题，能达到比Transformer更高的性能；Mamba则进一步通过输入依赖的选择机制和更快的硬件感知算法改进之。

2.2 模型结构设计

DiS参数化噪声预测网络${ϵ}_{\theta }(x_t,t,c)$，以时间$t$、条件$c$和噪声图像$x_t$，预测向$x_t$加入的噪声。DiS基于双向Mamba结构，如下图所示。

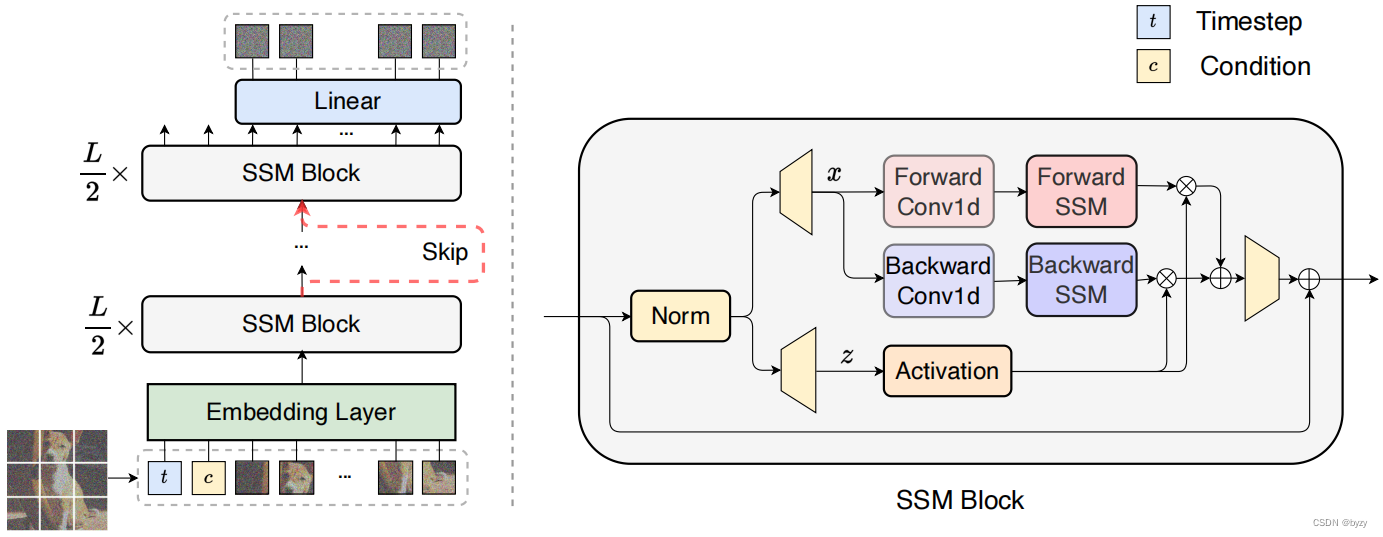
图像patch化：DiS的第一层将输入图像$I\in {\mathbb{R}}^{H\times W\times C}$转化为拉直的2D patch$X\in {\mathbb{R}}^{J\times (p^2\cdot C)}$。然后，通过对每个patch进行线性嵌入，转化为含$J$个token的、维度为$D$的序列。为每个输入token使用可学习位置编码。$J=\frac{H\times W}{p^2}$由patch大小$p$决定。

SSM块：输入token会被一组SSM块处理。SSM块的输入还包括时间$t$与条件$c$。本文使用双向序列建模，即SSM块的前向过程包含了前向和反向两个方向的处理。

跳跃连接：本文将$L$个SSM块分为前半和后半两部分，每部分$\lfloor \frac{L}{2}\rfloor$个。设$h_{shallow},h_{deep}\in {\mathbb{R}}^{J\times D}$分别为跳跃连接分支和主分支的隐状态，则通过拼接和线性投影后再送入下一个SSM块，即$\mathtt{Linear}(\mathtt{Concat}(h_{shallow},h_{deep}))$。

线性解码器：需要将最后一个SSM块的隐状态解码为噪声预测和对角化协方差矩阵（与原始输入尺寸相同）。本文使用线性解码器，即LayerNorm+线性层，将每个token转化为$p^2\cdot C$的张量。最后，将解码的token重排为原始大小，得到预测噪声与协方差。

条件引入：本文在输入token的序列上增加时间$t$与条件$c$的向量嵌入作为额外token（类似ViT中的类别token），从而无需修改SSM块。在最后一个SSM块后，从序列移除条件token。此外，还用自适应归一化层替换标准归一化层，使模型从$c$与$t$嵌入向量的和中回归缩放和偏移参数。

2.3 计算分析

对序列$X\in {\mathbb{R}}^{1\times J\times D}$和状态扩维默认设置$E=2$，自注意力与SSM的计算复杂度分别为$O(SA)=4J{D}^2+2J^{2}D$和$O(SSM)=3J(2D)N+J(2D)N^2$。

其中自注意力的计算是序列长度$J$的二次方，而SSM则是线性关系。注意$N$为固定参数。这说明DiS有较强的可放缩性。

3. 实验

3.1 实验设置

数据集：仅使用水平翻转数据增广。

实施细节：本文对DiS的权重使用指数移动平均方法。

3.2 模型分析

patch大小的影响：当模型大小一致时，减小patch大小（增加token数），性能会提高。这可能是扩散模型噪声预测任务的低级特性，导致需要小型patch，而不像更高级的分类任务。对高分辨率图像，使用小尺寸patch可能会引入高计算成本，可将图像转换为低维隐式表达，然后再使用DiS处理。

长跳跃的影响：比较拼接（$\mathtt{Linear}(\mathtt{Concat}(h_{shallow},h_{deep}))$）
、求和（$h_{shallow}+h_{deep}$）和无跳跃连接三种方式。实验表明，求和不会带来明显的性能提升，因为SSM自身可以通过线性方式保留一些浅层信息。而使用拼接和可学习的线性投影可以大幅增加性能。

条件组合：比较两种引入时间$t$的方案：（1）将$t$视为token，与图像patch一同处理；（2）将$t$的嵌入整合到SSM块的层归一化中，类似U-Net中的自适应分组归一化，得到自适应层归一化：$AdaLN(h,s)=y_s\mathtt{LayerNorm}(h)+y_b$，其中$h$为SSM的隐状态，$y_s,y_b$为时间嵌入的线性投影。实验表明前者的性能优于后者。

缩放模型大小：增大模型深度（SSM块层数）和宽度（隐状态维度）均能提高性能。

3.3 主要结果

无条件图像生成：DiS与基于U-Net或Transformer的扩散模型有相当的性能，但参数量更少。

以类别为条件的图像生成：本文的方法可以超过其余方法的性能。