- 1基于微信小程序图书销售商城系统设计与实现_基于微信小程序的图书销售系统设计与实现
- 2【ES一】SpringBoot2.x+ES8.11.1(windows环境)整合_springboot集成es8.11
- 3潜谈IT从业人员在传统IT和互联网之间的择业问题(上)-传统乙方形公司_乙方onsite
- 4华睿相机sdk 开发_相机SDK开发(示例代码)
- 5考研:中国科学院地理所历年GIS研究生入学考试真题汇总_gis考研真题
- 6解决stata安装外部命令报错cannot write in directory C:\Users\�ƿ���\ado\plus\_
- 7python延时队列_延时队列方案解析:redis-zset方案
- 8CPU密集型计算、IO密集型计算、多进程、多线程_计算密集型和io密集型 多线程和多进程
- 9repo镜像服务器搭建 思路_rk的repo仓库怎么搞
- 10Host头攻击-使用加密和身份验证机制
强化学习------PPO算法
赞
踩
简介
PPO 算法之所以被提出,根本原因在于 Policy Gradient 在处理连续动作空间时 Learning rate 取值抉择困难。
Learning rate 取值过小,就会导致深度强化学习收敛性较差,陷入完不成训练的局面,取值过大则导致新旧策略迭代时数据不一致,造成学习波动较大或局部震荡。除此之外,Policy Gradient 因为在线学习的性质,进行迭代策略时原先的采样数据无法被重复利用,每次迭代都需要重新采样;
同样地置信域策略梯度算法(Trust Region Policy Optimization,TRPO)虽然利用重要性采样(Important-sampling)、共轭梯度法求解提升了样本效率、训练速率等,但在处理函数的二阶近似时会面临计算量过大,以及实现过程复杂、兼容性差等缺陷。
而PPO 算法具备 Policy Gradient、TRPO 的部分优点,采样数据和使用随机梯度上升方法优化代替目标函数之间交替进行,虽然标准的策略梯度方法对每个数据样本执行一次梯度更新,但 PPO 提出新目标函数,可以实现小批量更新。
PPO 算法可依据 Actor 网络的更新方式细化为:
- 含有自适应 KL-散度
(KL Penalty)的 PPO-Penalty - 含有
Clippped Surrogate Objective函数的 PPO-Clip
下面我们一次介绍PPO算法的基本原理,以及 PPO-Penalty 和PPO-Clip两种形式的PPO算法
一、PPO原理
1、由On-policy 转化为Off-policy
- 如果被训练的
agent和与环境做互动的agent(生成训练样本)是同一个的话,那么叫做on-policy(同策略)。 - 如果被训练的
agent和与环境做互动的agent(生成训练样本)不是同一个的话,那么叫做off-policy(异策略)。
PPO算法是在Policy Gradient算法的基础上由来的,Policy Gradient是一种on-policy的方法,他首先要利用现有策略和环境互动,产生学习资料,然后利用产生的资料,按照Policy Gradient的方法更新策略参数。然后再用新的策略去交互、更新、交互、更新,如此重复。这其中有很多的时间都浪费在了产生资料的过程中,所以我们应该让PPO算法转化为Off-Policy。
Off-Policy的目的就是更加充分的利用actor产生的交互资料,增加学习效率。
2、Importance Sampling(重要性采样)
重要性采样(Importance Sampling)推导过程
Importance Sampling 是一种用于估计在一个分布下的期望值的方法。在强化学习中,我们需要估计由当前策略产生的样本的值函数,然后利用该估计值来优化策略。然而,在训练过程中,我们通常会使用一些已经训练好的旧策略来采集样本,而不是使用当前的最新策略。这就导致了采样样本和当前策略不匹配的问题,也就是所谓的“策略偏移”。
为什么要在PPO算法中使用Importance Sampling?
我们看一下Policy Gradient的梯度公式:
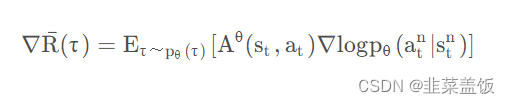
问题在于上面的式子是基于
τ
~
p
θ
(
τ
)
τ ~p_θ (τ)
τ~pθ(τ)采样的,一旦更新了参数,从θ到θ ′ ,这个概率
P
θ
P_{\theta}
Pθ就不对了。而Importance Sampling解决的正是从
τ
~
p
θ
(
τ
)
\tau~p_\theta(\tau)
τ~pθ(τ)采样,计算θ '的
∇
R
ˉ
(
τ
)
\nabla\bar{R}(\tau)
∇Rˉ(τ)的问题。
重要性采样(Importance Sampling)推导过程的推导可以点击链接查看,这里直接给出公式:
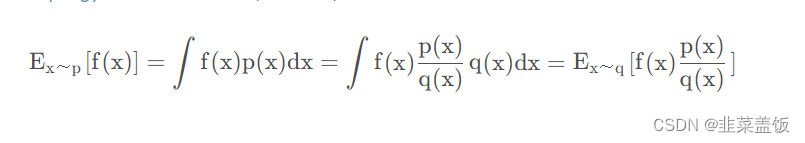
上面的式子表示,已知x服从分布p,我们要计算f(x),但是p不方便采样,我们就可以通过q去采样,计算期望。
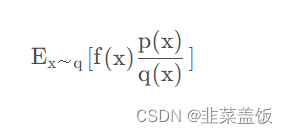
这里我们用q做采样,
p
(
x
)
q
(
x
)
\frac{p(x)}{q(x)}
q(x)p(x)叫做重要性权重,用来修正q与p两个分布的差异。理论上利用重要性采样的方法我们可以用任何q来完成采样,但是由于采样数量的限制,q与p的差异不能太大。如果差异过大
E
x
~
q
[
f
(
x
)
p
(
x
)
q
(
x
)
]
E _{x~q} [f(x) \frac{p(x)}{q(x)} ]
Ex~q[f(x)q(x)p(x)]与
E
x
~
q
[
f
(
x
)
]
E _{x~q} [f(x) ]
Ex~q[f(x)]的差异也会很大。
3、off-policy下的梯度公式推导
在on-policy情况下,Policy Gradient公式为:
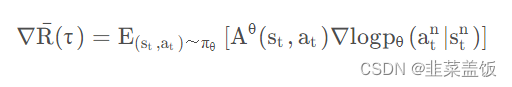
由上面的推导可得,我们利用
θ
′
\theta'
θ′ ,优化
θ
\theta
θ时的公式为:
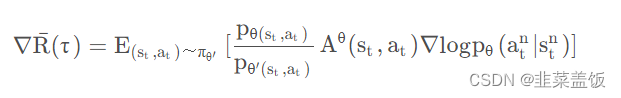
其中
A
θ
(
s
t
,
a
t
)
A^{\theta}(s_t, a_t)
Aθ(st,at)为比较优势,从该项的推导过程可以知道,它是由采样样本决定的,所以应该用
A
θ
′
(
s
t
,
a
t
)
A^{\theta'}(s_t, a_t)
Aθ′(st,at)表示,所以式子变为:
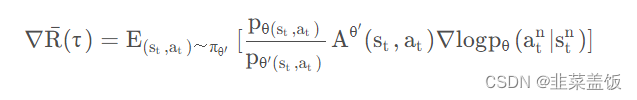
将
p
θ
(
s
t
,
a
t
)
p_{\theta(s_t,a_t)}
pθ(st,at) 展开可得:
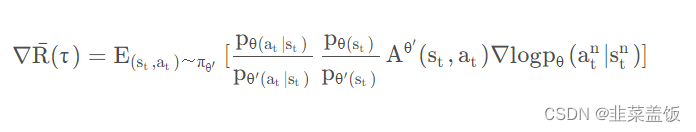
我们认为某一个状态
s
t
s_t
st出现的概率与策略函数无关,只与环境有关,所以可以认为
p
θ
(
s
t
)
≈
p
θ
′
(
s
t
)
p_{\theta(s_t)} \approx p_{\theta'(s_t)}
pθ(st)≈pθ′(st),由此得出如下公式:
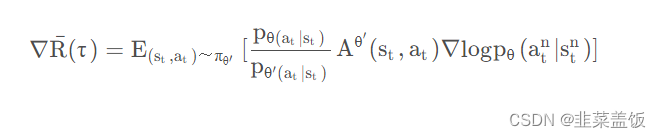
根据上面的式子,我们就可以完成off-policy的工作,反推出目标函数为:
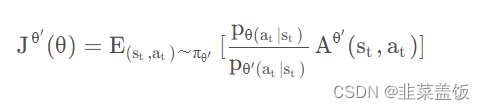
二、PPO算法两种形式
1、PPO-Penalty
PPO-Penalty 基于 KL散度惩罚项优化目标函数。
PPO-Penalty 的主要思想是将非负约束视为一种奖惩机制。具体来说,当一个行为不符合约束条件(比如动作小于0)时,我们会对策略进行惩罚。这种惩罚采用了一种类似于强化学习中的奖励机制的方式,即在损失函数中引入一个 penalty term。
例如,在 PPO-Penalty 中,我们可以将惩罚项添加到 PPO 算法的损失函数中,可以是在 KL 散度约束项的后面添加一个 penalty term 或者在损失函数中添加一个额外的 penalty term。这个 penalty term 会根据动作的非负性来惩罚那些不符合约束条件的行为,从而强制策略学会产生符合约束条件的行为。
用拉格朗日乘数法直接将KL散度的限制放入目标函数,变成一个无约束的优化问题。同时还需要更新KL散度的系数。
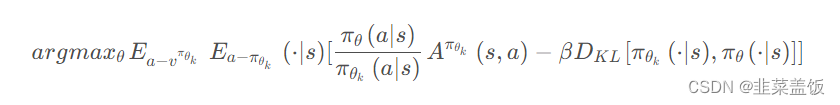
令
d
k
=
D
K
L
v
π
θ
k
[
π
θ
k
(
⋅
∣
s
)
,
π
θ
(
⋅
∣
s
)
]
d_k=D^{v^{\pi_{\theta_k}}}_{KL}[\pi_{\theta_k}(\cdot|s), \pi_{\theta}(\cdot|s)]
dk=DKLvπθk[πθk(⋅∣s),πθ(⋅∣s)]
- 如果 d k < δ / 1.5 d_k < \delta /1.5 dk<δ/1.5, 那么 β k + 1 = β k / 2 \beta_{k+1} = \beta_k/2 βk+1=βk/2
- 如果 d k > δ ∗ 1.5 d_k > \delta *1.5 dk>δ∗1.5, 那么 β k + 1 = β k / 2 \beta_{k+1} = \beta_k/2 βk+1=βk/2
- 否则 β k + 1 = β k \beta_{k+1} = \beta_k βk+1=βk
相对PPO-Clip来说计算还是比较复杂,我们在之后的例子使用PPO-Clip
2、PPO-Clip
PPO-Clip 的目标是在优化策略的同时,控制策略更新的幅度,以避免更新过大导致策略发生剧烈变化。这可以提供算法的稳定性,并且有助于收敛到一个比较好的策略。
具体来说,PPO-Clip 在优化过程中使用一个剪切函数来限制新旧策略之间的差异。这个剪切函数用于计算出新旧策略在每个动作样本上的比例,并将其与一个预先设定的范围进行比较。
剪切函数使用的是一个剪切比例,通常表示为 clip_ratio,它是一个介于0和1之间的数值。比如,如果 clip_ratio 设置为0.2,那么在计算新旧策略比例时,会将比例限制在0.8到1.2之间。
使用剪切函数,PPO-Clip 有两个重要的优点:
- 剪切目标:
PPO-Clip使用剪切函数来确保新策略更新不超过一个预定的范围,从而避免了过大的策略变化。这可以防止策略的不稳定性和发散,同时保证算法的收敛性。 - 改进策略更新:
PPO-Clip可以通过剪切目标的方式改进策略更新的效果。在优化过程中,通过比较新旧策略在每个样本上的比例,并选择较小的那个,可以保留原始策略中已经表现良好的部分,从而提高策略的稳定性和性能。
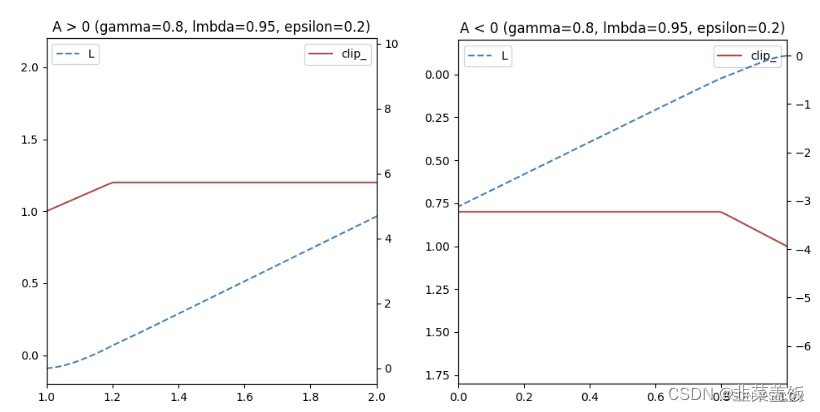
PPO-Clip直接在目标函数中进行限制,保证新的参数和旧的参数的差距不会太大。
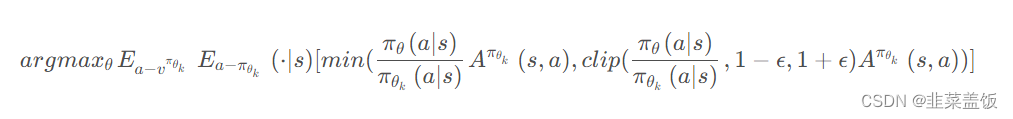
本质就是将新旧动作的差异限定在
[
1
−
ϵ
,
1
+
ϵ
]
[1-\epsilon, 1+\epsilon]
[1−ϵ,1+ϵ]。
如果A > 0,说明这个动作的价值高于平均,最大化这个式子会增大
π
θ
(
a
∣
s
)
π
θ
k
(
a
∣
s
)
\frac{\pi_\theta(a|s)}{\pi_{\theta_k}(a|s)}
πθk(a∣s)πθ(a∣s)但是不会让超过
1
+
ϵ
1+\epsilon
1+ϵ。反之,A<0,最大化这个式子会减少
π
θ
(
a
∣
s
)
π
θ
k
(
a
∣
s
)
\frac{\pi_\theta(a|s)}{\pi_{\theta_k}(a|s)}
πθk(a∣s)πθ(a∣s)但是不会让超过
1
−
ϵ
1-\epsilon
1−ϵ
可以简单绘制如下:
算法流程如下:

三、PPO算法实战
PPO-Clip更加简洁,同时大量的实验也表名PPO-Clip总是比PPO-Penalty 效果好。所以我们就用PPO-Clip算法进行代码实战。
我们使用使用的环境是OpenAI gym中的CartPole-v0环境
代码解释可以看代码中的注释,这里不再赘述
ppo_torch.py
import os import numpy as np import torch as T import torch.nn as nn import torch.optim as optim from torch.distributions.categorical import Categorical class PPOMemory: """ 经验池 """ def __init__(self, batch_size): self.states = [] self.probs = [] self.vals = [] self.actions = [] self.rewards = [] self.dones = [] self.batch_size = batch_size def generate_batches(self): n_states = len(self.states) batch_start = np.arange(0, n_states, self.batch_size) indices = np.arange(n_states, dtype=np.int64) np.random.shuffle(indices) batches = [indices[i:i + self.batch_size] for i in batch_start] return np.array(self.states), \ np.array(self.actions), \ np.array(self.probs), \ np.array(self.vals), \ np.array(self.rewards), \ np.array(self.dones), \ batches def store_memory(self, state, action, probs, vals, reward, done): self.states.append(state) self.actions.append(action) self.probs.append(probs) self.vals.append(vals) self.rewards.append(reward) self.dones.append(done) def clear_memory(self): self.states = [] self.probs = [] self.actions = [] self.rewards = [] self.dones = [] self.vals = [] class ActorNetwork(nn.Module): """ 构建策略网络--actor """ def __init__(self, n_actions, input_dims, alpha, fc1_dims=256, fc2_dims=256, chkpt_dir='tmp/ppo'): super(ActorNetwork, self).__init__() self.checkpoint_file = os.path.join(chkpt_dir, 'actor_torch_ppo') self.actor = nn.Sequential( nn.Linear(*input_dims, fc1_dims), nn.ReLU(), nn.Linear(fc1_dims, fc2_dims), nn.ReLU(), nn.Linear(fc2_dims, n_actions), nn.Softmax(dim=-1) ) self.optimizer = optim.Adam(self.parameters(), lr=alpha) self.device = T.device('cuda:0' if T.cuda.is_available() else 'cpu') self.to(self.device) def forward(self, state): """ 返回动作的概率分布 :param state: :return: """ dist = self.actor(state) dist = Categorical(dist) return dist # 返回动作的概率分布 def save_checkpoint(self): """ 保存模型 :return: """ T.save(self.state_dict(), self.checkpoint_file) def load_checkpoint(self): """ 加载模型 :return: """ self.load_state_dict(T.load(self.checkpoint_file)) class CriticNetwork(nn.Module): """ 构建价值网络--critic """ def __init__(self, input_dims, alpha, fc1_dims=256, fc2_dims=256, chkpt_dir='tmp/ppo'): super(CriticNetwork, self).__init__() self.checkpoint_file = os.path.join(chkpt_dir, 'critic_torch_ppo') self.critic = nn.Sequential( nn.Linear(*input_dims, fc1_dims), nn.ReLU(), nn.Linear(fc1_dims, fc2_dims), nn.ReLU(), nn.Linear(fc2_dims, 1) ) self.optimizer = optim.Adam(self.parameters(), lr=alpha) self.device = T.device('cuda:0' if T.cuda.is_available() else 'cpu') self.to(self.device) def forward(self, state): value = self.critic(state) return value def save_checkpoint(self): """ 保存模型 :return: """ T.save(self.state_dict(), self.checkpoint_file) def load_checkpoint(self): """ 加载模型 :return: """ self.load_state_dict(T.load(self.checkpoint_file)) class Agent: def __init__(self, n_actions, input_dims, gamma=0.99, alpha=0.0003, gae_lambda=0.95, policy_clip=0.2, batch_size=64, n_epochs=10): self.gamma = gamma self.policy_clip = policy_clip self.n_epochs = n_epochs self.gae_lambda = gae_lambda # 实例化策略网络 self.actor = ActorNetwork(n_actions, input_dims, alpha) # 实例化价值网络 self.critic = CriticNetwork(input_dims, alpha) # 实例化经验池 self.memory = PPOMemory(batch_size) def remember(self, state, action, probs, vals, reward, done): """ 记录轨迹 :param state: :param action: :param probs: :param vals: :param reward: :param done: :return: """ self.memory.store_memory(state, action, probs, vals, reward, done) def save_models(self): print('... saving models ...') self.actor.save_checkpoint() self.critic.save_checkpoint() def load_models(self): print('... loading models ...') self.actor.load_checkpoint() self.critic.load_checkpoint() def choose_action(self, observation): """ 选择动作 :param observation: :return: """ # 维度变换 [n_state]-->tensor[1,n_states] state = T.tensor([observation], dtype=T.float).to(self.actor.device) # 当前状态下,每个动作的概率分布 [1,n_states] dist = self.actor(state) # 预测,当前状态的state_value [b,1] value = self.critic(state) # 依据其概率随机挑选一个动作 action = dist.sample() probs = T.squeeze(dist.log_prob(action)).item() action = T.squeeze(action).item() value = T.squeeze(value).item() return action, probs, value def learn(self): # 每次学习需要更新n_epochs次参数 for _ in range(self.n_epochs): # 提取数据集 state_arr, action_arr, old_prob_arr, vals_arr, \ reward_arr, dones_arr, batches = \ self.memory.generate_batches() values = vals_arr advantage = np.zeros(len(reward_arr), dtype=np.float32) # 计算优势函数 for t in range(len(reward_arr) - 1): # 逆序时序差分值 axis=1轴上倒着取 [], [], [] discount = 1 a_t = 0 for k in range(t, len(reward_arr) - 1): a_t += discount * (reward_arr[k] + self.gamma * values[k + 1] * \ (1 - int(dones_arr[k])) - values[k]) discount *= self.gamma * self.gae_lambda advantage[t] = a_t advantage = T.tensor(advantage).to(self.actor.device) # 估计状态的值函数的数组 values = T.tensor(values).to(self.actor.device) for batch in batches: # 获取数据 states = T.tensor(state_arr[batch], dtype=T.float).to(self.actor.device) old_probs = T.tensor(old_prob_arr[batch]).to(self.actor.device) actions = T.tensor(action_arr[batch]).to(self.actor.device) # 用当前网络进行预测 dist = self.actor(states) critic_value = self.critic(states) critic_value = T.squeeze(critic_value) # 每一轮更新一次策略网络预测的状态 new_probs = dist.log_prob(actions) # 新旧策略之间的比例 prob_ratio = new_probs.exp() / old_probs.exp() # prob_ratio = (new_probs - old_probs).exp() # 近端策略优化裁剪目标函数公式的左侧项 weighted_probs = advantage[batch] * prob_ratio # 公式的右侧项,ratio小于1-eps就输出1-eps,大于1+eps就输出1+eps weighted_clipped_probs = T.clamp(prob_ratio, 1 - self.policy_clip, 1 + self.policy_clip) * advantage[batch] # 计算损失值进行梯度下降 actor_loss = -T.min(weighted_probs, weighted_clipped_probs).mean() returns = advantage[batch] + values[batch] critic_loss = (returns - critic_value) ** 2 critic_loss = critic_loss.mean() total_loss = actor_loss + 0.5 * critic_loss self.actor.optimizer.zero_grad() self.critic.optimizer.zero_grad() total_loss.backward() self.actor.optimizer.step() self.critic.optimizer.step() self.memory.clear_memory()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
main.py
import gym import numpy as np from ppo_torch import Agent from utils import plot_learning_curve if __name__ == '__main__': print('开始训练!') env = gym.make('CartPole-v0') # 每经过N步就更新一次网络 N = 20 batch_size = 5 # 每次更新的次数 n_epochs = 4 # 学习率 alpha = 0.0003 # 初始化智能体 agent = Agent(n_actions=env.action_space.n, batch_size=batch_size, alpha=alpha, n_epochs=n_epochs, input_dims=env.observation_space.shape) # 训练轮数 n_games = 300 # 统计图 figure_file = 'plots/cartpole.png' # 存储最佳得分 best_score = env.reward_range[0] # 存储历史分数 score_history = [] # 更新网络的次数 learn_iters = 0 # 每一轮的得分 avg_score = 0 # 总共在环境中走的步数 n_steps = 0 # 开始玩游戏 for i in range(n_games): observation = env.reset() done = False score = 0 while not done: action, prob, val = agent.choose_action(observation) observation_, reward, done, info = env.step(action) env.render() n_steps += 1 score += reward # 存储轨迹 agent.remember(observation, action, prob, val, reward, done) if n_steps % N == 0: # 更新网络 agent.learn() learn_iters += 1 observation = observation_ score_history.append(score) avg_score = np.mean(score_history[-100:]) # 比较最佳得分 保存最优的策略 if avg_score > best_score: best_score = avg_score agent.save_models() print('episode', i, 'score %.1f' % score, 'avg score %.1f' % avg_score, 'time_steps', n_steps, 'learning_steps', learn_iters) x = [i+1 for i in range(len(score_history))] plot_learning_curve(x, score_history, figure_file)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
画图工具
utils.py
import numpy as np
import matplotlib.pyplot as plt
def plot_learning_curve(x, scores, figure_file):
running_avg = np.zeros(len(scores))
for i in range(len(running_avg)):
running_avg[i] = np.mean(scores[max(0, i-100):(i+1)])
plt.plot(x, running_avg)
plt.title('Running average of previous 100 scores')
plt.savefig(figure_file)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
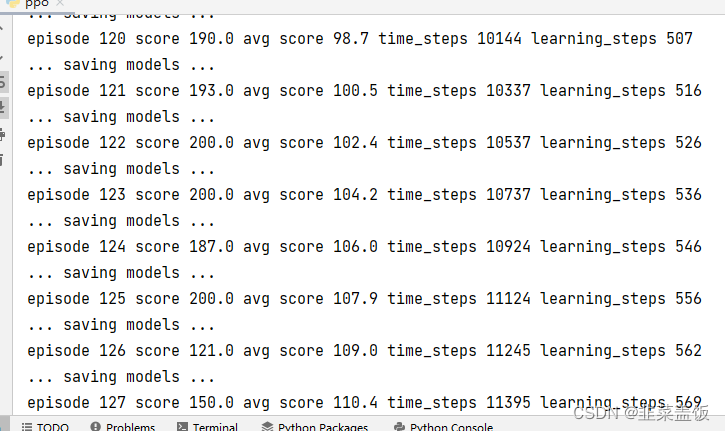
效果如下: