数据结构-树（c语言实现篇）_c语言实现树

数据结构之二叉树（c语言实现篇）

介绍树的概念和二叉树的概念和应用，内容主要是以二叉树为主。

1. 树

1.1 树的概念

树是n个结点的有限集，当n=0时，称为空树。树是一种非线性的数据结构，与前面的线性表、栈和队列是不同的。树的根节点没有前驱，除了根节点外的所有结点有且只有一个前驱。树中所有结点可以有零个或多个后继。

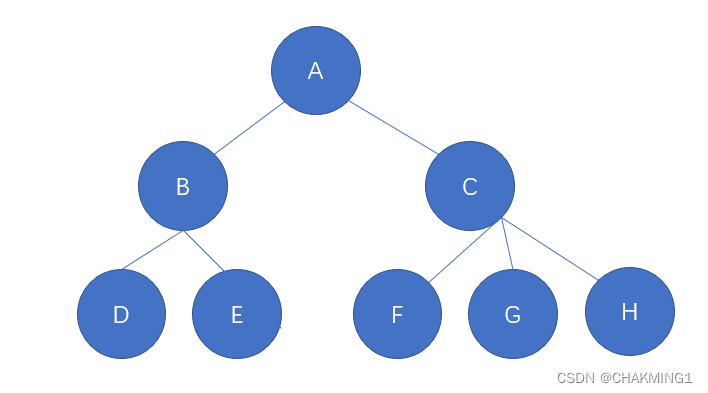
1.2 树的相关概念

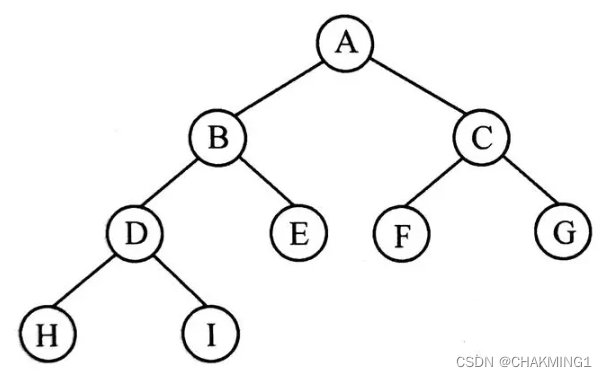
结点的度：一个结点有多少颗子树，子树的个数就是该结点的度，例如B结点有两颗子树，度为2。

叶子结点或终端结点：度为0的结点称为叶子结点也叫作终端结点。例如H和J都是叶子结点。

非终端结点和分支结点：度不为0的结点就叫作分支结点或者非终端结点。例如D和C都是分支结点。

双亲结点或父节点：若一个结点有子结点，也就是该结点不是叶子结点，那么它是它子节点的父节点。例如D是H和J的父节点。

孩子结点或者子结点：一个结点含有子树的根节点就是该节点的子节点。例如D和E是B的孩子结点。

兄弟结点：具有相同父结点的结点互相称为兄弟结点。例如H和I互为兄弟结点。

树的度：一棵树中，最大结点的度称为树的度，例如该树的度为2。

结点的层次：从跟开始定义起，根为第一层，根的子节点第二层，以此类推。

树的高度或深度：树种节点的最大层次。例如，该树的高度为4。

堂兄弟结点：两个结点的父节点为兄弟结点。例如，E和F为堂兄弟结点。

结点的祖先：从根节点到该节点所经过的分支上的所有结点都是该节点的祖先结点，包括父节点。例如，A是所有结点的祖先结点，

子孙结点：以某结点为根的子树上的任意结点都是该节点的子孙结点，例如所有结点都是A结点的子孙结点。

森林：由m颗(m>0)互不相交的树的集合称为森林。

1.3 树的表示方式

树相对于线性表复杂许多，既可以采用顺序存储结构，又可以采用链式存储结构。这里介绍三种常用的存储结构。

1.3.1 双亲表示法

这种存储结构采用一组连续空间来存储每个结点，同时每个结点增加一个伪指针，指向它的双亲结点在数组中的位置。根节点没有双亲结点，所以伪指针为-1。

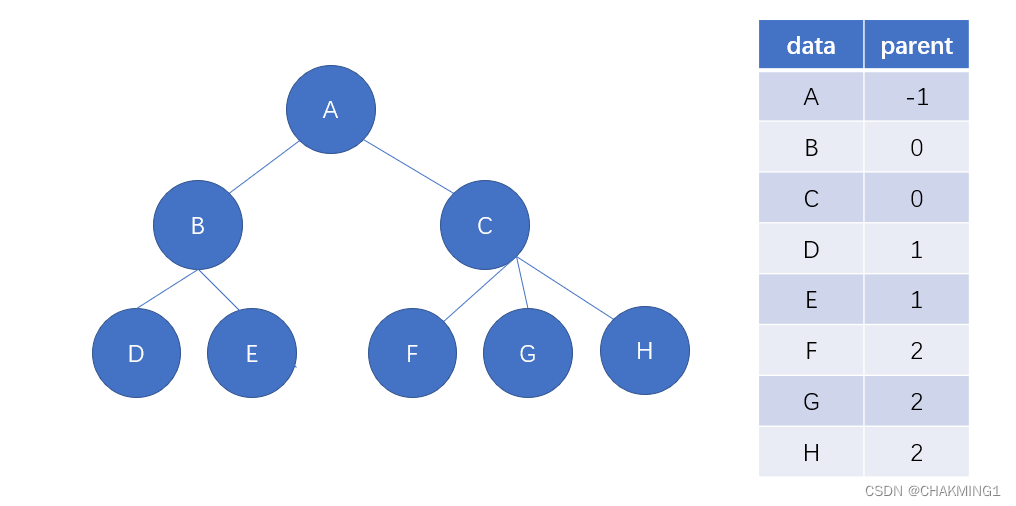
1.3.2 孩子表示法

孩子表示法是将每个结点的孩子结点用单链表形成一个线性结构。

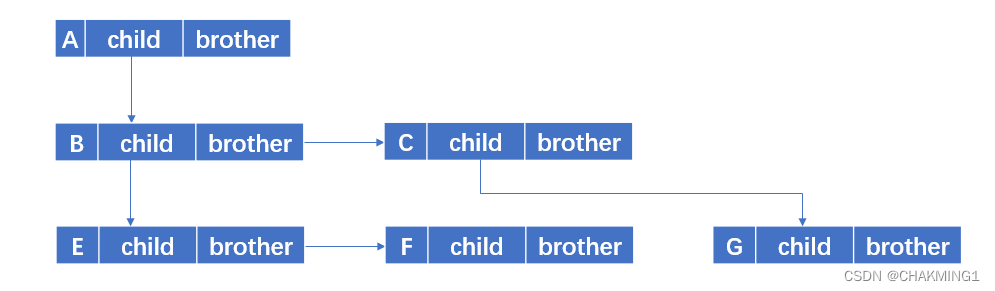
1.3.3 孩子兄弟表示法

孩子兄弟表达式又称为二叉树表示法，用二叉链表作为树的存储结构。每个结点包含三个部分：结点的值，第一个孩子的结点，指向其下一个兄弟结点。

typedef int DataType;
struct node {
	struct node* _firstChild;
       struct node* _nextBrother;
       DataType _data;
};
1
2
3
4
5
6

1.4 树的现实应用

比如某学院下的不同系的不同教室

或者是我们的硬盘上的文件，等等。

2.二叉树的概念及结构

2.1 二叉树的定义

二叉树是树形结构中的一种特殊结构，其特点是每个结点最多有两颗子树，且子树有左右之分，并且次序不可颠倒，是一颗有序树。二叉树同样也是n个结点的有限集合，有五种形态基本形态：

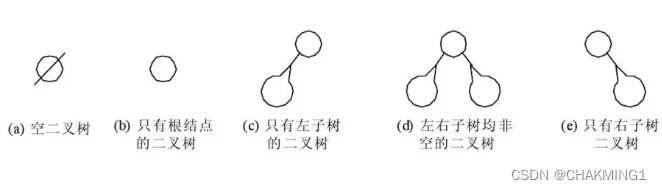
几个特殊的二叉树：

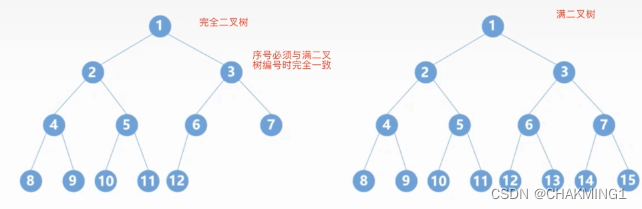
（1）满二叉树：一棵树的高度为h，含有2^h-1个结点的二叉树称为满二叉树。树种的每一层都拥有最多结点，也就叶子结点都集中在最下面的一层，并且除了该层外的每个结点都有两个孩子结点。

（2）完全二叉树：高度为h，有n个结点，每个结点与其满二叉树中树的编号一一对应，称为完全二叉树。所以满二叉树又是一种特殊的完全二叉树。

（3）二叉排序树。左子树上的所有结点的值均小于根节点的值，右子树上所有结点的值均大于根节点的值。左右子树同样是一颗二叉排序树。

（4）平衡二叉树。树上任一结点的左子树和右子树的深度相差不超过1。

2.2 二叉树的性质

1. 非空二叉树的叶子结点数等于度为2的结点数加1，即n0 = n2 + 1。
2. 非空二叉树上第k层上最多有2^(k-1)个结点。
3. 高度为h的二叉树最多有2^h - 1个结点。
4. 具有n个结点的完全二叉树的高度为log2(n+1)向上取整。
5. 对于具有n个结点的完全二叉树，如果按照从上到下、从左到右依次对所有结点按顺序开始编号，则有以下关系：
   1. 若i>0,i位置的双亲结点位置为(i-1)/2，i等于0时，为根节点，无双亲结点
   2. 若2i+1<n，左孩子序号为2i+1,2i+1>=n无左孩子
   3. 若2i+2<n，右孩子序号为2i+2,2i+2>=n无右孩子

2.3 二叉树的存储结构

2.3.1 顺序存储结构

二叉树的顺序存储结构是指用一组地址连续的存储单元依次从上而下、自左向右存储完全二叉树上的结点元素，按照编号从0~n，如果当前不存在该节点，用一个特殊的值表示（-1），该二叉树和它对应的完全二叉树的编号要完全一致，所以采用完全二叉树或者满二叉树去使用顺序存储最为合适。

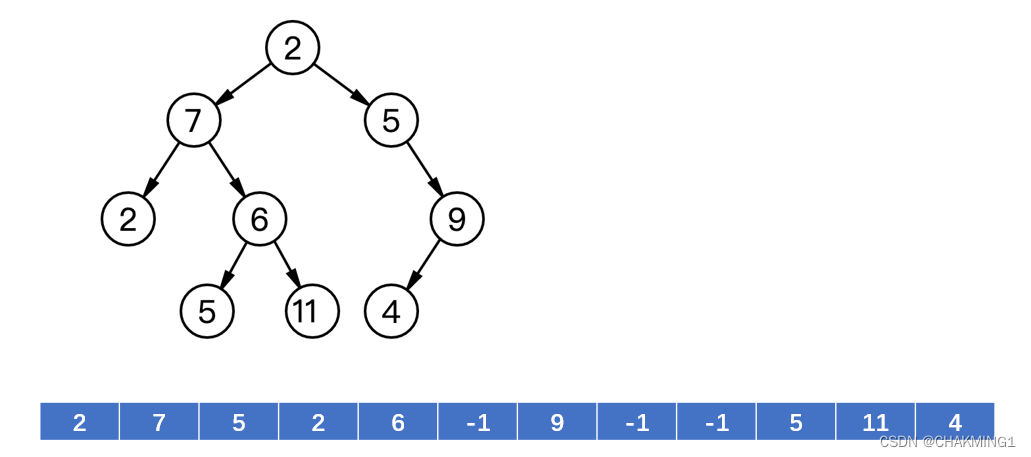
2.3.2 链式存储结构

由于顺序存储的空间利用率比较低，因此二叉树一般采用链式存储结构，链式存储结构的结点包含三个部分，分别是数据域、左指针域、右指针域。

(1) 二叉链表表示法

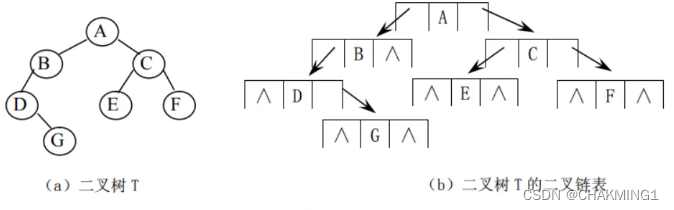
typedef int BTDataType;
// 二叉链表
struct BinaryTreeNode
{
	struct BinaryTreeNode* _pLeft; // 指向当前结点的左孩子
	struct BinaryTreeNode* _pRight; // 指向当前结点的右孩子
	BTDataType _data; // 数据域
};
1
2
3
4
5
6
7
8

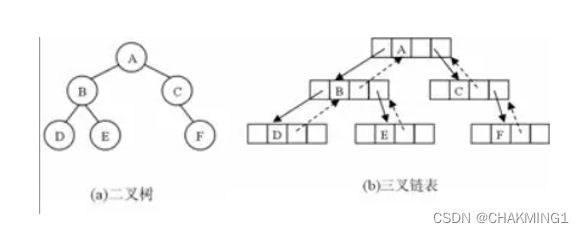
（2）三叉链表表示法

typedef int BTDataType;
// 二叉链表
struct BinaryTreeNode
{
	struct BinaryTreeNode* _pParent; // 指向当前结点的双亲
	struct BinaryTreeNode* _pLeft; // 指向当前结点的左孩子
	struct BinaryTreeNode* _pRight; // 指向当前结点的右孩子
	BTDataType _data; // 数据域
};
1
2
3
4
5
6
7
8
9

对比：二叉链表，通常只需要表示孩子结点，而三叉链表适用于经常需要找到该结点的父亲结点。